SMA 滑动摩擦阻尼器的数值模拟及参数分析

邱灿星，刘家旺，杜修力

(北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124)

为了保障结构在地震作用下的安全，结构被动控制技术以其效果良好、构造简单、易于维护等优点，在学术研究和工程实践中均引起广泛兴趣[1]。传统的延性设计思想，允许结构主体通过塑性损伤来满足变形需求和消耗地震能量；与之相比，采用消能减震思想则，可以利用阻尼器进行有效耗散地震能量，减少重要构件遭遇的永久性损伤[2-4]。

然而，传统阻尼器通常不具有自复位能力，这使得结构在震后可能存在较大的残余变形，造成结构或非结构构件的破坏。不仅如此，残余变形是评价结构抗震韧性的重要指标，相关研究表明，当残余位移角超过0.5%时，修复成本将高于重建投入[5]。所以，若阻尼器具有自复位能力，则可在耗散地震能量的同时帮助结构减小残余变形，从而有效提高结构的抗震韧性。

超弹性形状记忆合金(shape memory alloy，SMA)可以在材料层面实现阻尼器乃至结构体系的自复位能力。超弹性SMA 可在室温下拥有“旗帜形”的滞回曲线，在耗能的同时自发地恢复非线性变形[6]。这种性质是由于外荷载造成的应力引发了SMA 由奥氏体向马氏体的正相变，而这种状态在常温下是不稳定的；卸载后，SMA 将自发地开始马氏体到奥氏体的逆相变，从而恢复变形。近年来，学术界提出了多种基于超弹性SMA 的自复位阻尼器[7-17]。李惠和毛晨曦[7]提出了拉伸型和剪刀型两种SMA 阻尼器；钱辉等[8]结合SMA 丝与摩擦板设计了SMA 摩擦复合阻尼器；Qiu 和Zhu[9]通过振动台试验验证了SMA 支撑钢框架的抗震性能；孙彤和李宏男[10]设计了一种能将扭转运动转化为拉伸的SMA 丝材阻尼器；黄宙等[11]基于杠杆原理设计了自复位放大位移型SMA 阻尼器；Fang 等[12]提出了基于SMA 碟簧的自复位阻尼器；Qiu 等[13-14]研发了基于防屈曲SMA 棒的自复位阻尼器和SMA-钢阻尼器。

近年来，学者们也在积极探索斜面摩擦消能机制在自复位装置中的应用。Hashemi 等[18]提出了一种韧性滑动摩擦节点；Hu 等[19]利用楔形摩擦块研发了自复位阻尼装置和相应的结构体系；Zhang 等[20]结合楔形摩擦块和SMA 棒设计了一种自复位阻尼器。受到现有研究成果的启发，本文将超弹性SMA 棒与斜面变摩擦机制结合，提出了一种新型阻尼器，即SMA 滑动摩擦阻尼器(shape memory alloy slip friction damper， SMASFD)。SMASFD 使用SMA 螺栓作为预紧力元件，摩擦斜面作为主要消能机制。该阻尼器构造简单、安装方便，其滞回性能可通过改变SMA 螺栓的尺寸和类型以及摩擦面的摩擦系数和倾角等参数进行调节，在使用时可以灵活设计。本文首先介绍了阻尼器的基本构造和工作机理，之后给出了预测其滞回行为的理论公式，开展了概念验证试验，在ABAQUS 软件中建立了三维实体有限元模型进行数值模拟和参数分析。

1 SMA 滑动摩擦阻尼器 SMASFD

1.1 基本构造

阻尼器的基本构造如图1(a)所示，其主要部件包括夹板、盖板、SMA 螺栓、垫块、垫片和螺母等。SMA 螺栓贯穿夹板、盖板、垫块和垫片，两端通过螺母连接并可起到预紧效果。除SMA 螺栓外，其余构件的材料均为钢材。各部件之间无需焊接，易于安装或拆卸。

图1 SMA 滑动摩擦阻尼器Fig. 1 SMASFD

如图1(b)所示，SMA 螺栓由SMA 棒材加工而成，两端加工出螺纹段以方便连接，中间加工出削弱段，以期SMA 螺栓的轴向变形集中于削弱段，避免连接端的破坏，螺纹段和削弱段之间加工出圆弧过渡段以防应力集中。夹板和盖板加工成可贴合的斜面，盖板上加工圆孔使SMA 螺栓穿过。夹板上加工槽孔以允许其与盖板之间产生相对滑动。设置垫块的目的在于匹配SMA 螺栓的长度。值得说明的是，该示意图中仅采用了2 根SMA螺栓，在实际应用时，SMA 螺栓的数量可根据需要增加。

1.2 变形模式

阻尼器的变形模式如图2 所示。当阻尼器受拉或受压时，两块夹板相对于盖板向外或向内滑动，夹板的斜面扩大盖板间的距离，并使SMA 螺栓伸长。SMA 螺栓因伸长而产生的轴力使盖板与夹板的接触面间产生法向压力，进而在接触面上产生摩擦力。阻尼器的自复位能力由SMA 螺栓的超弹性和斜面摩擦机制共同提供，耗能主要来源于摩擦机制和SMA 自身的耗能。值得一提的是，夹板与盖板之间的法向接触力随SMA 螺栓的变形而发生变化，因此是变摩擦机制。

图2 阻尼器的变形模式Fig. 2 Deformation mode of damper

1.3 理论公式

阻尼器的滞回行为由摩擦和SMA 螺栓的受拉行为控制。图3(a)为SMA 螺栓轴向受拉循环时的力-位移简化曲线，其中fMs和fMf分别为SMA 正相变开始和结束时对应的SMA 螺栓轴力，fAs和fAf分别为SMA 逆相变开始和结束时对应的SMA螺栓轴力。图3(b)展示了阻尼器的理想滞回行为。加载时，SMA 螺栓发生正相变时对应的阻尼器输出力为FMs，随后阻尼器的刚度降低；继续加载至SMA 螺栓的正相变结束时，阻尼器的输出力为FMf；若继续加载，SMA 螺栓进入应变强化阶段，阻尼器的刚度明显增大，如图3(b)的虚线所示。卸载时，SMA 螺栓发生逆相变，起始和结束时对应的阻尼器输出力分别为FAs和FAf。

图3 阻尼器的理想力学行为Fig. 3 Idealized mechanical behaviors of damper

图4(a)和图4(b)分别展示了加载阶段和卸载阶段的受力分析，由于阻尼器的构造对称，仅取一半结构进行分析。根据静力平衡原理，可以得到：

式中：F和F′分别为加载阶段和卸载阶段的输出力；nb为单侧SMA 螺栓的数量；θ 为斜面倾角；µ为接触面动摩擦系数；f为SMA 螺栓的轴力。

根据几何关系，阻尼器的变形量Δ和SMA 螺栓的轴向拉伸变形量δ 具有如下关系：

SMA 螺栓的内力可按下式计算：

式中，σ 和A分别为SMA 螺栓削弱段的应力和横截面面积。

为保证阻尼器在震后完全自复位，卸载后的输出力不能为负，根据式(2)可得：

此外，若阻尼器的变形过大会使夹板滑出原斜面，阻尼器也将丧失自复位能力。因此，阻尼器的最大变形量Δmax需要满足下式：

式中，L为单个斜面的水平长度，如图4(a)所示。

图4 阻尼器的受力分析Fig. 4 Free body diagram of damper

同时，当SMA 完成正相变后，将进入应变强化阶段，这会引起强度的陡增甚至产生残余位移[21]。因此，阻尼器的最大变形量还应满足：

式中，δMf为SMA 螺栓正相变结束所对应的变形量，如图3(a)所示。式(1)表明，当SMA 的材料类型和螺栓的尺寸及数量已知时，2nbf的值即可完全确定；对F进行正则化处理，即F/2nbf，则阻尼器的力学性能由斜面倾角和摩擦系数决定。在满足完全自复位的前提下，图5(a)和图5(b)分别显示了改变斜面倾角和摩擦系数对阻尼器正则化强度的影响。可以发现，阻尼器的正则化强度随着斜面倾角和摩擦系数的增大而增大。例如，在µ=0.3的条件下，当θ 从20°增大到65°时，阻尼器的正则化强度从0.75 增大到6.85；在tanθ=0.3 的条件下，当µ从0 增大到0.3 时，阻尼器的正则化强度从0.3 增大到0.7。这表明，即使SMA 螺栓的数量和力学性能是确定的，阻尼器的承载力仍然具有较大的取值范围。

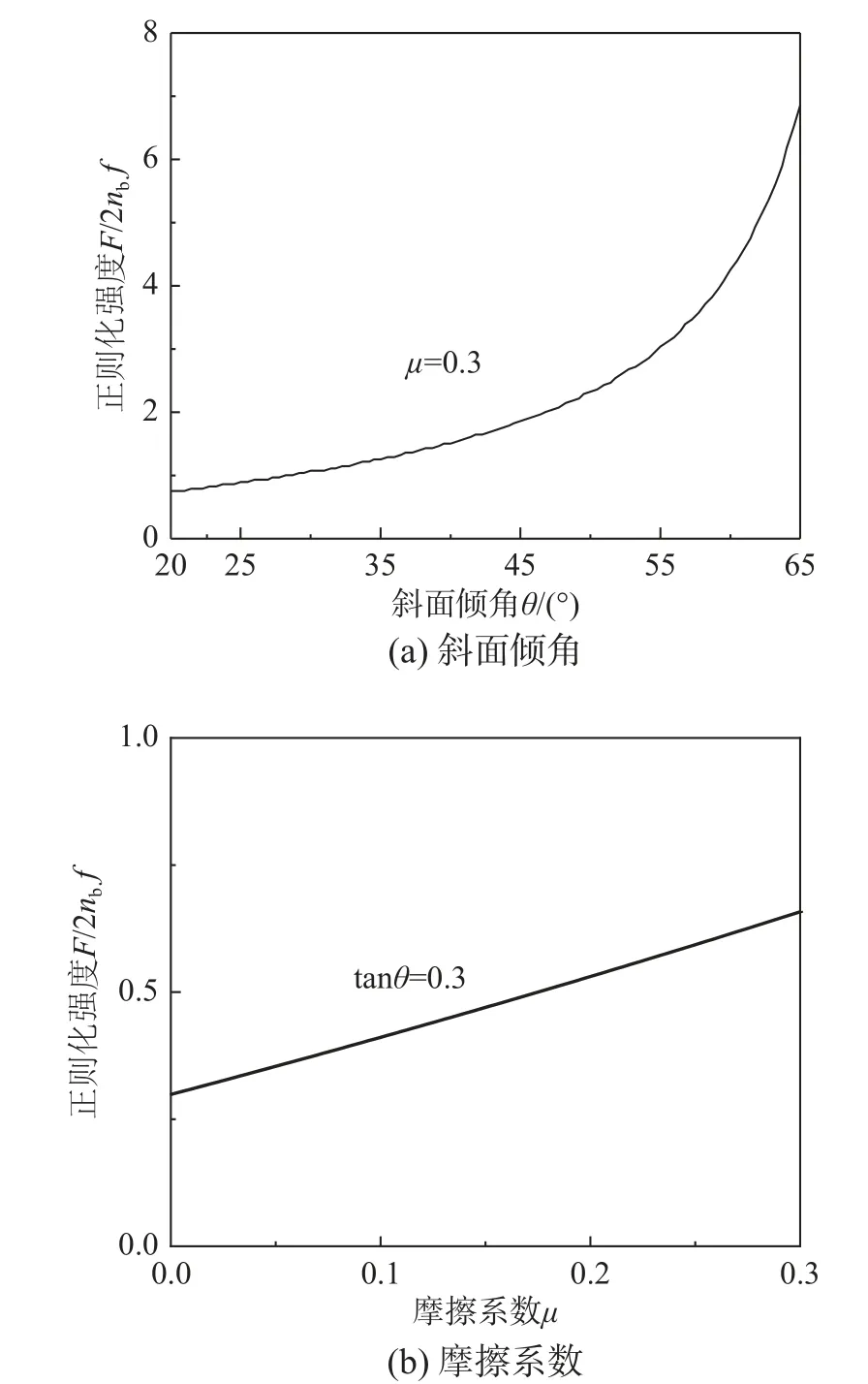
图5 斜面倾角和摩擦系数对阻尼器正则化强度的影响Fig. 5 Effects of groove angle and friction coefficient on regularized strength of damper

还需要注意的是，各关键参数的取值不应导致传力构件屈服。在本文中，夹板是传力构件，其屈服强度为：

式中：σy为钢材的屈服强度；Ap为斜面交界处的横截面面积。

1.4 概念验证试验

为了验证该新型阻尼器的概念，笔者加工了一个试件并开展了拟静力试验。需要说明的是，本文的主要目的是推导阻尼器滞回行为的理论公式和建立有限元数值模型，并侧重于通过有限元数值模拟来开展参数分析，因此，本文未系统地介绍试验研究。由于是概念验证试验，本试验中的SMA 螺栓、夹板和盖板等的尺寸与下文中有限元模型所采用的不尽相同。图6(a)展示了用于该阻尼器的SMA 螺栓，其原始直径为12 mm，加工后的削弱段直径为8 mm，削弱段长度为100 mm，螺纹段长度为40 mm。为测得摩擦面之间的摩擦系数，加工了摩擦面试件并进行试验，如图6(b)所示，其高强螺栓施加15 kN 预紧力。该阻尼器试件采用了2 根SMA 螺栓，盖板和夹板采用Q345钢，摩擦斜面倾角为16.7°。图6(c)所示为阻尼器试件已安装就位，加载设备为250 kN 液压伺服疲劳试验机。试验时，使用试验机内置的力传感器和外置的百分表分别记录荷载和变形。图6(d)为SMA 螺栓循环拉伸试验结果，呈现出“旗帜形”滞回曲线。图6(e)为摩擦面试件试验结果，其摩擦性能稳定，动摩擦系数为0.15。阻尼器试验以SMA 螺栓削弱段的应变为控制因素，采用位移加载，加载的位移幅值对应SMA 螺栓削弱段的应变为5%。图6(f)为阻尼器试验结果，可以看到阻尼器的滞回曲线呈“旗帜形”，具有良好的耗能能力和优越的自复位能力。理论计算和数值模拟的结果如图6(f)所示，二者均与试验结果吻合良好，说明理论公式和有限元模拟均较为准确。

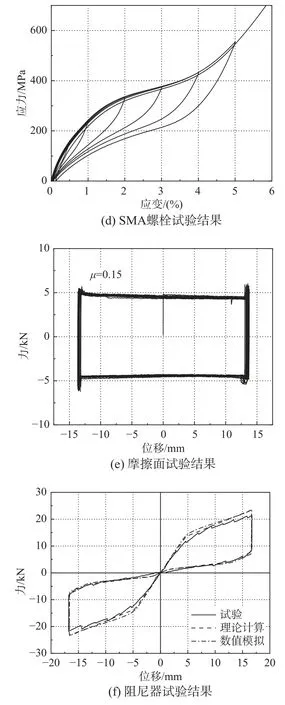
图6 概念验证试验Fig. 6 Proof-of-concept test

2 数值模拟

2.1 有限元模型

为了进一步掌握阻尼器的工作原理，特别是观察关键构件的局部行为，本节采用软件ABAQUS 建立有限元模型。需要再次说明的是，有限元模型中的构件尺寸与概念验证试验中的不完全相同。尽管如此，这并不妨碍通过数值模拟手段理解阻尼器的滞回行为。图7 展示了阻尼器主要构件的具体尺寸，其中SMA 螺栓削弱段的长度为100 mm，削弱段直径为14 mm，盖板与夹板斜面倾角的正切值为tanθ=6/20=0.3。

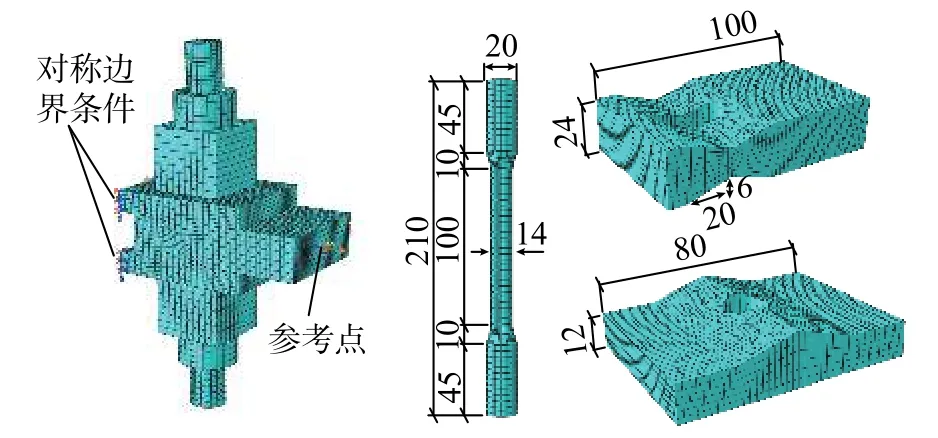
图7 阻尼器的ABAQUS 有限元模型Fig. 7 FE model of damper in ABAQUS

所有部件均采用三维实体单元建模，单元类型为8 节点六面体线性缩减积分单元(C3D8R)。由于阻尼器具有对称的构造和变形模式，为了节省计算成本和提高计算效率，取半结构建立模型进行模拟计算，盖板在分割面处设置对称的边界条件。各构件接触面之间的接触关系采用“面与面接触”模拟，法向接触行为模式为“硬接触”，切向接触行为选用“罚函数”以模拟摩擦行为。为了简化模型，SMA 螺栓的螺纹段并未模拟，而是将该段的外表面与螺母的内壁设置为“绑定”约束。为模拟加卸载过程，夹板端面与参考点设置“耦合”约束，并将位移荷载施加在参考点上。接触面的摩擦系数设置为0.15[22]。SMA 螺栓、盖板和夹板的网格尺寸均设置为2 mm。以SMA 螺栓削弱段的应变控制加载位移的幅值，本文选取的应变范围为1%～5%。采用ABAQUS 中自带的超弹性本构模型模拟SMA 的力学行为，图8(a)展示了各个材料参数的含义，其中σMs和σMf分别为SMA 正相变开始和结束时的应力，σAs和σAf分别为逆相变开始和结束时的应力，EA和EM分别为奥氏体和马氏体的模量，εL为相变应变。SMA的材料属性的取值见表1，数据来源于文献[23]。如图8(b)所示，钢材采用理想弹塑性材料。盖板、夹板和垫块的屈服强度fy取345 MPa，螺母的屈服强度fy取640 MPa，钢材的弹性模量E均为206 GPa，泊松比均为0.3，考虑0.1%的屈服后硬化[24]。

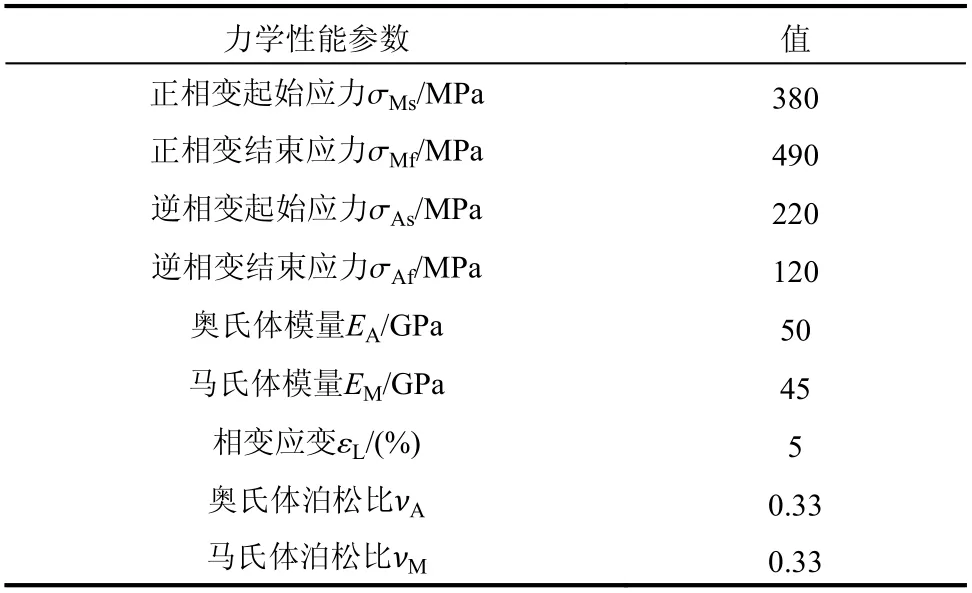
表1 SMA 的材料属性[23]Table 1 Material properties of SMA[23]

图8 SMA 和钢材的本构模型Fig. 8 Constitutive models of SMA and steel

2.2 模拟结果

首先单独模拟SMA 螺栓的拉伸循环行为，位移幅值对应削弱段的1%～5%应变，得到的结果如图9 所示，可见SMA 螺栓展示了“旗帜形”滞回曲线。在验证了SMA 螺栓之后，继续模拟阻尼器的往复加载行为。图10(a)和图10(b)分别为阻尼器在最大受拉受压下的应力和应变云图，该剖面图可方便观察SMA 螺栓的受力及变形状态。通过变形图可知，阻尼器展现出了预期的变形模式：无论受拉或受压时，夹板与盖板发生相对滑动，SMA螺栓总是被拉伸，应变集中于SMA 螺栓的削弱段，并且沿长度方向均匀变形。图11 对比了数值模拟和理论公式的结果，可见二者完全吻合，验证了有限元模型的准确性，但是二者均有待于进一步的试验验证。根据图12 的定义，滞回性能参数包括加载阶段最大输出力Fmax、卸载阶段最大输出力、最大变形Δmax、割线刚度K、最大单圈耗能WD和等效粘滞阻尼比ξ。在最大位移幅值时，上述各值分别为63.6 kN、18.9 kN、16.7 mm、3.8 kN/mm、1559.7 J 和23.4%。

图9 SMA 螺栓在往复拉伸下的滞回曲线Fig. 9 Hysteresis of SMA bolt under cyclic tensile loading

图10 阻尼器在最大变形时的应力和应变云图Fig. 10 Stress and strain contour plots of damper under maximum deformation

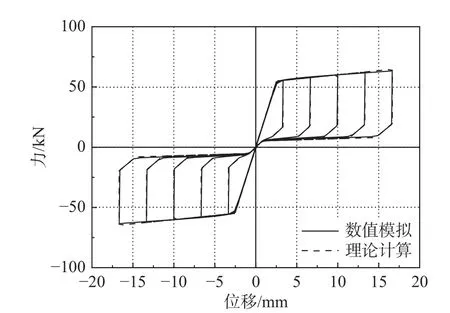
图11 数值模拟结果与理论计算结果的对比Fig. 11 Comparison of numerical simulation and analytical method

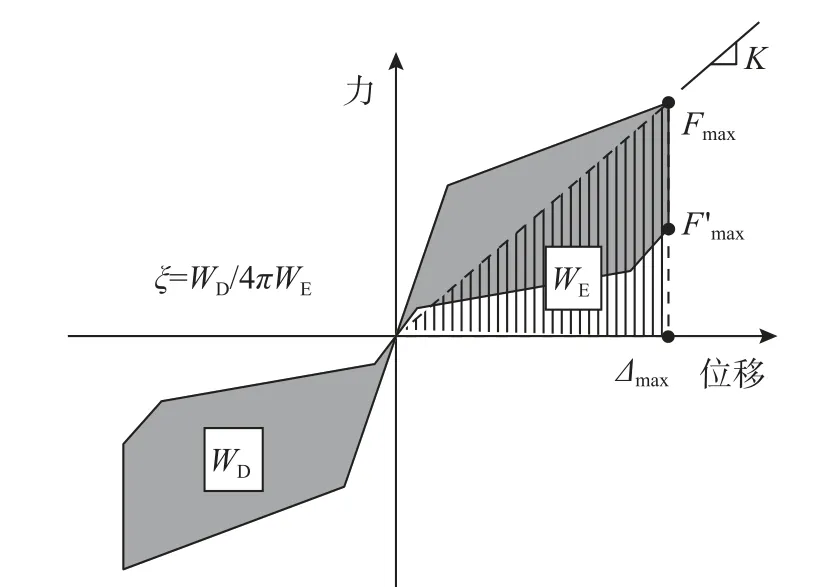
图12 关键滞回性能参数Fig. 12 Key parameters of hysteretic properties

3 参数分析

尽管理论公式能够预测设计参数对阻尼器整体力学行为的影响，但是各关键部件的局部行为，包括应力、应变和变形等，却不易直接观察。因此，本节基于有限元数值模型开展参数分析。关键参数包括：斜面倾角、摩擦系数和SMA螺栓的预紧力。将第2 节介绍的模型作为标准模型，编号为S1，其余6 个模型的编号为S2～S7。各模型所对应的具体参数见表2。S2～S7 仅改变了一项参数，模型的其他信息等均与S1 一致。加载位移仍由SMA 螺栓削弱段的应变进行控制。表2列出了各模型的设计参数和由模拟结果得到的最大变形时的滞回性能参数。S3 和S5 具有较大的Fmax，其夹板和盖板的应力云图如图13 所示，可以发现夹板和盖板承受了较高的应力需求，例如，夹板斜面靠近槽孔位置存在较大应力，S3 和S5 的最大应力分别为295 MPa 和325 MPa，已接近屈服力345 MPa。因此，在实际设计中，应对阻尼器的夹板和盖板进行强度验算，避免二者屈服。此外，模拟结果还表明，盖板和夹板的截面突变处有较大的应力。因此，在实际使用时，宜将盖板和夹板的截面突变处加工为圆角，起到减轻应力集中和磨损的效果。

表2 各模型参数Table 2 Parameters of models

图13 S3 和S5 中夹板和盖板的应力云图Fig. 13 Stress contour plots of cap and middle plates of S3 and S5

3.1 斜面倾角

为检验斜面倾角对阻尼器滞回性能的影响，将S2 和S3 的tanθ 分别设置为0.2 和0.4。根据式(1)，阻尼器的输出力随tanθ 的增大而增大；阻尼器的变形能力不仅取决于夹板开孔大小、SMA 螺栓变形能力和斜面水平长度等因素，而且根据式(3)可知，改变斜面倾角会改变阻尼器变形量和SMA 螺栓变形量之间的关系。根据式(7)，阻尼器的变形不应使SMA 螺栓进入强化阶段。因此，阻尼器的变形能力还受制于SMA 螺栓削弱段的应变。对比时，以SMA 螺栓削弱段的应变为控制变量，故对S1～S3 采用不同的加载位移幅值。图14 对比了三者的滞回曲线，可以看到，S3 的强度大于S1和S2，而S2 具有最大的变形能力。S1～S3 的割线刚度分别为3.8 kN/mm、2.0 kN/mm 和6.4 kN/mm。当阻尼器变形为10 mm 时，S1～S3 的单圈滞回耗能分别为840.4 J、639.2 J 和1055.4 J。可见，增大斜面倾角会提高阻尼器的强度、割线刚度和耗能能力，不过变形能力会减小。

图14 斜面倾角的影响Fig. 14 Effect of groove angle

3.2 摩擦系数

阻尼器可以选取各种摩擦面材料，如钢-钢、黄铜板-钢、铝板-钢等，来改变摩擦系数，也可以通过在接触面加润滑材料以减小摩擦系数。为验证摩擦系数的影响，将S4 和S5 的摩擦系数分别设置为0 和0.3。对比如图15 所示。可以发现，摩擦系数越大，阻尼器的滞回曲线越饱满。最大变形时，S1 和S4、S5 的割线刚度分别为3.8 kN/mm、2.4 kN/mm 和5.3 kN/mm，等效粘滞阻尼比分别为23.4%、14.4%和27.3%。当摩擦系数较大时，阻尼器的强度、割线刚度和耗能能力均得到提高。与其他模型相比，S4 的滞回曲线并没有出现卸载时的垂直下降段，这是因为S4 的摩擦系数为0。值得注意的是，S5 的tanθ=µ=0.3，F′=0，滞回曲线的卸载阶段是一条与水平坐标轴重合的直线。若进一步增大摩擦系数将使阻尼器失去自复位能力，这与理论公式预计的结果一致。因此，为保证阻尼器的自复位能力，应确保摩擦系数小于斜面倾角的正切值。

图15 摩擦系数的影响Fig. 15 Effect of friction coefficient

3.3 SMA 螺栓的预紧力

为保证阻尼器的自复位能力或实现较大初始刚度，可对SMA 螺栓施加预紧力[25]。根据相关研究[25]，SMA 螺栓的预紧力不宜超过65%fMs，为检验预紧力对阻尼器滞回性能的影响，对S6 和S7的SMA 螺栓分别施加30%fMs(17.5 kN)和60%fMs(35.1 kN)的预紧力。S1 和S6、S7 的滞回曲线对比如图16 所示。S1 和S6、S7 的最大变形分别为16.7 mm、15.9 mm 和15.1 mm，增大预紧力减弱了阻尼器的变形能力。这是因为位移加载幅值由SMA 螺栓削弱段的应变控制，而预紧力会在SMA 螺栓中产生初始应变。由式(1)可知，阻尼器的最大输出力与SMA 螺栓的最大轴力成正比，由于所有模型的最大变形均对应于SMA 螺栓削弱段的5%应变，故S1、S6 和S7 的最大输出力相等。处于最大变形时，S1 和S6、S7 的割线刚度分别为3.8 kN/mm、4.0 kN/mm 和4.2 kN/mm，等效粘滞阻尼比分别为23.4%、24.3%和24.4 %。可见，施加预紧力可提高阻尼器的割线刚度和等效粘滞阻尼比，但是以减小最大变形能力为代价。

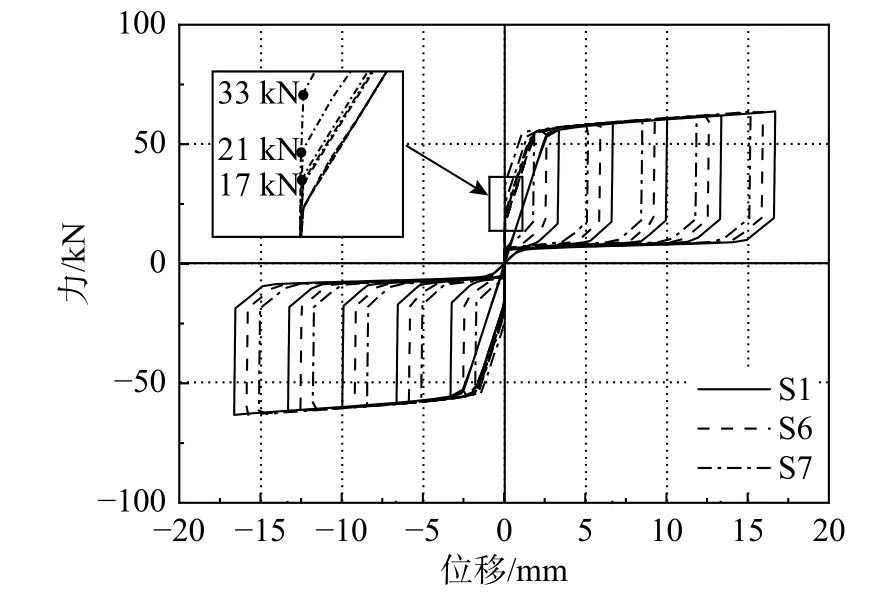
图16 SMA 螺栓预紧力的影响Fig. 16 Effect of preloading level of SMA bolts

需要注意的是，当外荷载克服预紧力后，夹板才开始滑动。当预紧力不超过fAf时，预紧力损失不会发生。S6 的起滑力始终为17 kN，而S7 的起滑力在第一圈加载时为33 kN，在随后的循环中逐渐下降至21 kN。该现象可由图17 解释。当预紧力大于fAf时，预拉伸长度将大于δAf，此时SMA螺栓处于点a 状态。当完成第一圈加卸载过程，即线a-b-c，可以发现，虽然SMA 螺栓的变形恢复到了预拉伸长度，但预紧力从点a 下降到了点c，产生了预紧力损失。当完成第二圈加卸载过程，即点c-d-e，预紧力从点c 下降到了点e。因此，若对SMA 螺栓施加大于fAf的预紧力，阻尼器第一圈加载的起滑力最大，之后预紧力会随着循环加载次数的增加而逐渐降低，阻尼器的起滑力会逐渐降低。在参数分析中，SMA 螺栓的fAf(18.5 kN)大于S6 的30%fMs(17.5 kN)，而小于S7 的60%fMs(35.1 kN)，所以预紧力损失现象只出现在了S7 中。作为进一步验证，提取模拟结果中的SMA 螺栓轴力，图18 展示了S7 的SMA 螺栓轴力随加载循环次数的变化，虚线标出了预紧力损失的现象。这说明，阻尼器的预紧力损失是由于SMA 材料本身的性质造成的，所以该现象在设计时应予以考虑。

图17 预紧力的损失Fig. 17 Loss of preloading level

图18 S7 的SMA 螺栓轴力随循环次数的变化Fig. 18 Changes of axial force in SMA bolts of S7 with cycle loadings

4 结论

本文介绍了SMASFD 的基本构造及工作原理，给出了预测其滞回行为的理论公式，开展了概念验证试验，建立了有限元模型，并基于有限元模型开展参数分析，研究了关键参数对阻尼器滞回性能的影响，主要结论如下：

(1) 理论分析、试验数据和数值模拟均表明SMASFD 的滞回曲线呈“旗帜形”，阻尼器具有良好的耗能能力和优越的自复位能力；阻尼器的等效阻尼比约为20%。提出的理论公式和建立的三维实体有限元模型均可以准确模拟其变形模式和滞回行为。

(2) 参数分析结果表明，增大斜面倾角可提高阻尼器的强度、割线刚度和耗能能力；当接触面间的摩擦系数较大时，阻尼器的强度、割线刚度和耗能能力得到提高，但超过上限值会导致阻尼器无法自复位；盖板和夹板需满足强度要求，截面的变化部位宜加工成圆角等光滑的过渡形式；对SMA 螺栓施加预紧力可提高阻尼器的初始刚度和割线刚度，但降低了阻尼器的最大变形能力。