改进的降阶牛顿迭代数值子结构方法

2022-08-01孙宝印孙天舒欧进萍

工程力学 2022年8期

孙宝印，申伟，孙天舒，欧进萍,4

(1. 河海大学土木与交通学院，江苏，南京 210098；2. 广西大学土木建筑工程学院，广西，南宁 530004；3. 大连理工大学土木工程学院，辽宁，大连 116024；4. 哈尔滨工业大学土木工程学院，黑龙江，哈尔滨 150090)

计算效率和模拟精度是高层建筑等重大工程地震弹塑性全过程分析的关键技术瓶颈。一方面，此类结构的规模庞大，为了精确刻画其非线性行为，有必要针对整体结构建立精细化的有限元模型，自由度动辄数十上百万，结构刚度矩阵的集成和分解耗时严重。更为关键的是，结构一旦进入非线性状态，传统的变刚度法需要反复迭代更新结构刚度，计算效率更是成为棘手难题。另一方面，高层结构地震倒塌破坏主要是由局部关键构件严重损伤导致，而这部分关键构件的非线性变形特征具有显著的多样性和复杂性，对模型精细程度提出了较高的要求。实际工程中为了满足计算效率要求，无法针对整体结构建立精细模型，进而难以保证局部关键构件的模拟精度。由此可见，计算效率和模拟精度之间相互矛盾、制约。现有的计算方法较难有效兼顾这类大规模结构非线性分析的效率和精度，因此，发展更加高效、精确的非线性分析理论和计算方法十分必要。

高层结构在地震作用下呈现局部非线性特征，如何充分利用这种局部化特征来提高大规模结构非线性分析的计算效率，是近几十年来国内外学者关注的重点。Clough 等[1]利用子结构方法对局部非线性的大规模结构系统进行动力分析。将整体结构划分为线弹性和塑性区域：一方面，通过静力凝聚消去线弹性区域内部自由度，降低求解矩阵规模来提高计算效率；另一方面，提高塑性区模型精细程度来有效兼顾模拟精度。Wong 等[2]提出拟力法，定义能够描述结构构件非线性行为的塑性自由度，建立相应的塑性机制，来模拟结构的非线性行为。并采用初始刚度对状态方程进行迭代求解，利用显式求解算法，可实现高效、稳定的结构非线性分析。随后，Li 等[3-5]在拟力法的基础上作了进一步改进，将材料应变分解为线弹性应变和非线性应变两部分，并在单元内构造非线性应变的分布场模型，提出了单元非线性变形机制的模拟方法。再结合虚功原理，建立具有隔离非线性特征的结构控制方程，在该方程迭代分析时仅需对一个小规模的Schur 补矩阵进行迭代更新，从而能够显著提高结构非线性分析的计算效率。此外，陆新征等[6]、Sun 等[7-8]以及陈宇等[9]从多尺度建模角度，对整体结构进行差异化建模分析，在保证模拟精度的前提下，可大幅降低结构模型自由度。

传统的子结构方法、拟力法以及多尺度方法均需要预判结构的塑性区域，并且模型网格一旦确认，分析过程中较难更改。为了规避这些缺陷，孙宝印等[10-13]提出数值子结构方法(如图1所示)，将原始高层结构的非线性分析转化为主结构的等效线弹性分析和屈服构件的隔离子结构非线性分析。在整个地震弹塑性时程分析过程中，由线弹性主结构模型计算得到整体结构的动力响应，根据结构全局位移实时判断构件的屈服状态。将构件屈服隔离并建立精细化的子结构模型，由子结构非线性分析计算得到屈服构件的真实内力，并将其传回主结构。主结构将转化得到的屈服构件等效外荷载作为外力项施加在屈服构件端部节点上，最后，再由主结构进行等效线弹性分析得到整体结构的真实响应。经研究表明：该方法可以有效兼顾大规模结构非线性分析的计算效率和模拟精度。

由于上述数值子结构方法采用初始弹性刚度进行非线性迭代分析，仍存在一定不足。于是，本文拟对该方法作进一步改进，提出一种降阶的牛顿迭代数值子结构方法。首先，简介数值子结构方法基本原理及其不足；其次，提出降阶的牛顿迭代算法，并介绍屈服构件的隔离子结构非线性分析；最后，通过一平面15 层3 跨钢结构的地震弹塑性时程分析来验证所提方法的精度和效率。

1 数值子结构方法基本原理及不足

1.1 数值子结构方法

根据数值子结构方法基本原理[10-13]，结构运动方程可以表示为：

式中：U、和分别为结构的位移、速度和加速度；M、C0、K0、F和Fc分别为结构的质量矩阵、初始阻尼矩阵、初始刚度矩阵、外力和非线性修正力，分别表示为：

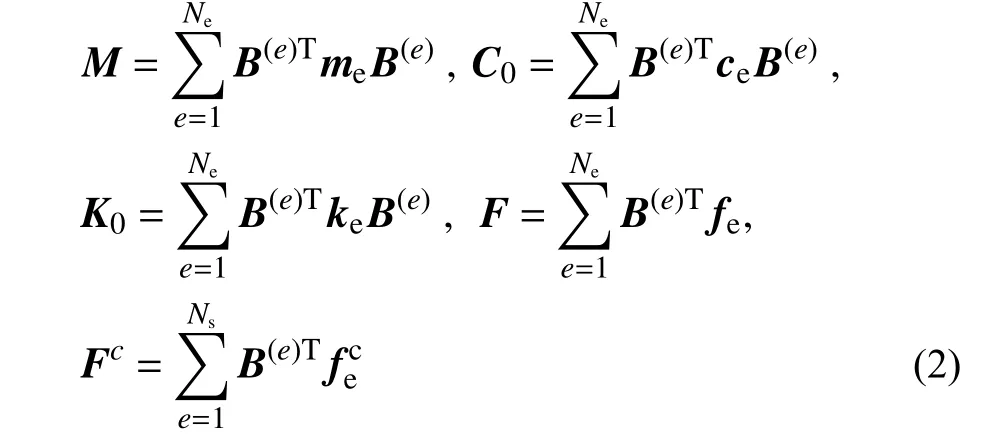
式中：Ne和Ns分别为总单元数和屈服单元数；B(e)为用于检索结构中单元所在位置的布尔矩阵；为屈服单元的非线性修正力，可表示为：

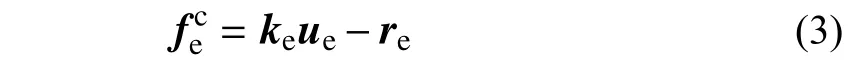
式中：ke和ue分别为屈服单元的初始弹性刚度和节点位移；re为由隔离子结构计算得到的屈服单元内力。

式(1)等式左边是一个线弹性系统，结构非线性是由等式右边的非线性修正力Fc来考虑。对于局部非线性结构系统，屈服单元数Ns＜＜Ne远小于总单元数Ne，则非线性修正力Fc的计算量较小。

1.2 数值子结构方法的不足

以文献[14]中15 层3 跨的平面钢框架结构为研究对象。采用不动点迭代数值子结构方法[10-13]对其进行地震弹塑性时程分析时，主结构中每根梁柱构件由30 个基于欧拉-伯努利梁理论的弹性单元模拟，分析过程中根据截面最外侧应变是否超过材料屈服应变来判断构件的弹塑性状态[15]，屈服单元由隔离子结构进行非线性分析。在隔离子结构中，屈服单元采用基于欧拉-伯努利梁理论的分布式塑性铰纤维单元模拟，钢材采用OpenSees中Steel02 本构模型模拟，材料弹性模量E=2.0×106MPa，硬化比b=0.1。在不同工况和收敛误差下，不动点迭代数值子结构方法的迭代次数时程曲线如图2 所示，迭代信息如表1 所示。可以看出，当收敛误差为1.0×10-5mm 时，8 度和9 度罕遇地震作用下，数值子结构方法需要最多24 步和26 步收敛，平均迭代次数分别为4.6 和6.9；而当收敛误差减小至1.0×10-8mm 时，最多需要41 步和44 步，平均迭代次数分别为7.1 和11.1。当荷载水平增大或收敛误差减小，不动点迭代数值子结构方法所需的迭代收敛次数均有所增加，尤其是当收敛条件变得苛刻，收敛速率显著降低。于是，下文将对该方法作进一步改进，以提高其收敛速率。

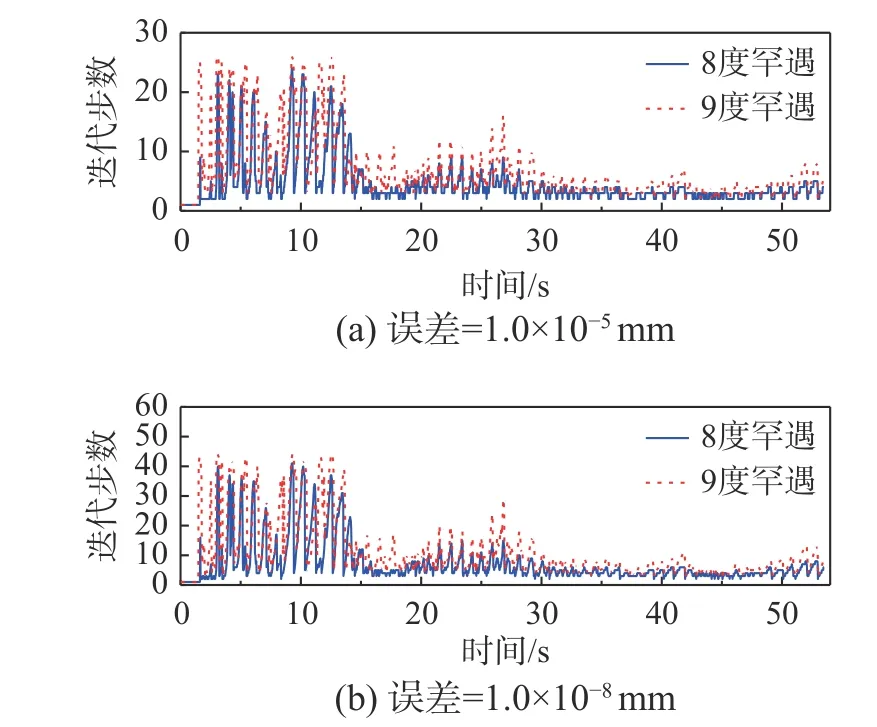
图2 不动点迭代数值子结构方法迭代次数时程曲线Fig. 2 Iteration number time-history curves using the numerical substructure method based on fixed-point iteration

表1 不动点迭代数值子结构方法迭代信息统计表Table 1 Table of iteration information using the numerical substructure method based on fixed-point iteration

2 降阶的牛顿迭代算法

经过时间离散后，第n时步结构的等效运动方程满足：

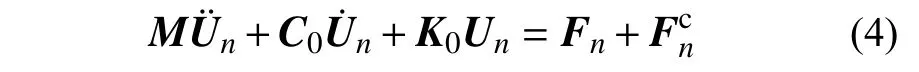
不失一般性，以Newmark-β 逐步积分法为例，第n时步速度和位移分别表示为：

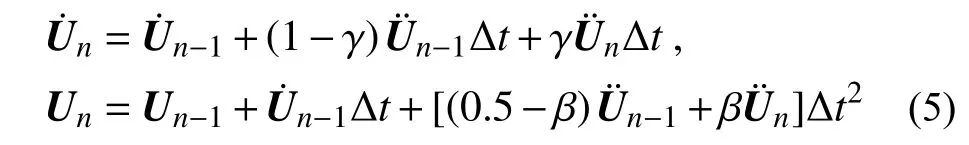
式中， γ 和 β为控制参数。本文采用平均加速度法，则 γ 和 β取值分别为0.5 和0.25。

由式(5)可以得到第n时步速度和加速度：

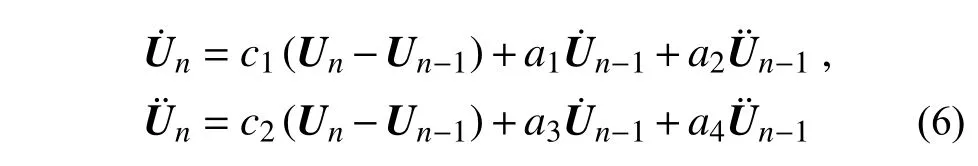
式中：c1=γ/(βΔt)；c2=1/β(Δt)2；a1=1-γ/β；a2=(1-γ/2β)Δt；a3=-1/βΔt；a4=1-1/2β。

将式(6)代入式(4)，得到结构的等效平衡方程：

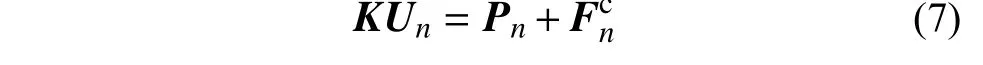
式中，K和Pn分别为结构等效初始刚度和外力：

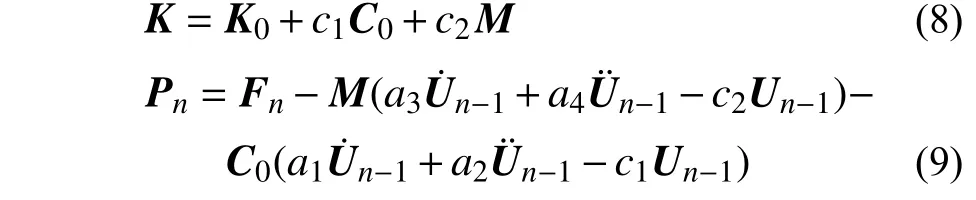
由式(7)可以得到结构的位移场：

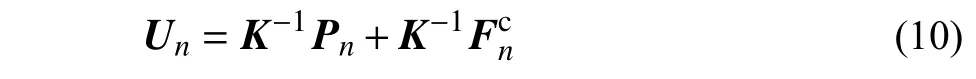
定义与屈服单元有关的自由度为塑性自由度，则塑性自由度位移us,n可以表示为：

式中，Bs,n为检索塑性自由度位置的布尔矩阵。

将式(10)代入式(11)，塑性自由度位移残差φ(us,n)可以表示为：

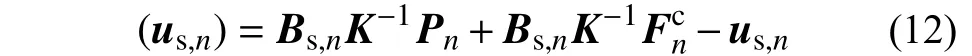
采用牛顿迭代算法，已知当前塑性自由度位移us,n和残差φ(us,n)，得到更新后的塑性自由度位移：

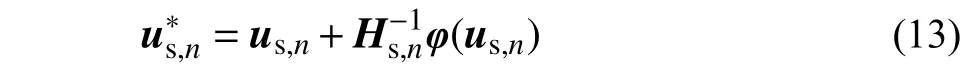
式中，Hs,n为与塑性自由度有关的迭代矩阵：

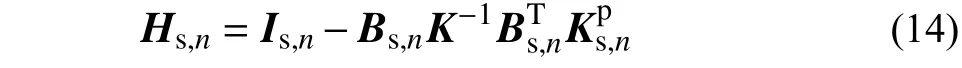
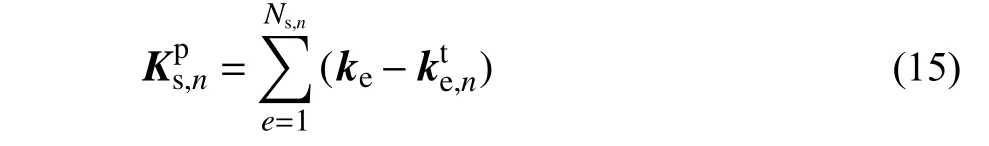
3 隔离子结构非线性分析

考虑到高层结构在地震作用下发生倒塌破坏，局部关键构件非线性程度较高，而大部分屈服构件的非线性程度较低(称之为一般屈服构件)。为了满足模拟精度需求，一般屈服构件和少数关键构件所采用的隔离子结构模型的精细程度不同。为了简化起见，本节以梁柱构件为例说明。

3.1 一般屈服梁柱构件

针对一般屈服梁柱构件，纤维模型可以较为准确模拟其非线性行为。由于主、子结构中梁柱构件均为杆系模型，它们的边界自由度一致，因此，由隔离子结构可直接计算得到屈服构件内力和切线刚度，这里不作详细赘述。

3.2 关键梁柱构件

以如图3(a)所示的平面框架结构为例，将主结构中关键柱构件隔离并建立精细化的子结构模型(例如：实体单元)，如图3(b)所示。为了消除刚体位移的影响，将主结构中屈服构件对应的弹性单元节点位移ue转换得到局部坐标位移ve：

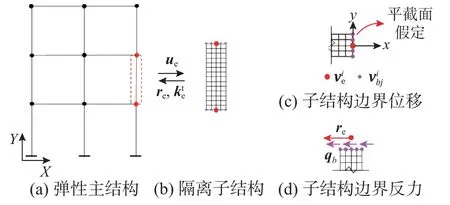
图3 关键构件隔离子结构精细化模型边界处理Fig. 3 Boundary treatment of isolated refined substructures for key components

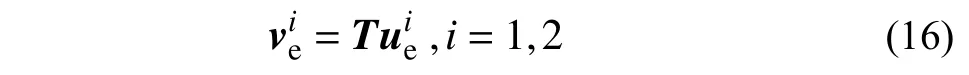
式中：上标i为精细化子结构第i个边界；转换矩阵T可以表示为：

式中， α为杆系单元轴向与全局坐标系X轴之间的夹角。

如图3(c)所示，在局部坐标系下，根据平截面假定，精细化子结构中第i个边界中第j个节点的位移满足以下转换关系：

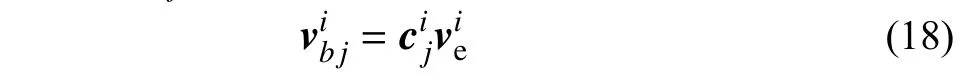
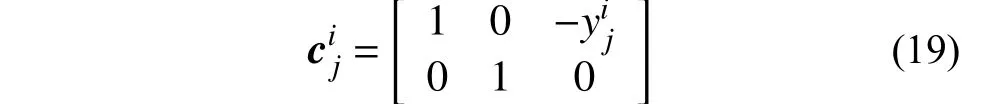
将式(16)代入式(18)，并集成得到全局坐标系下精细化子结构的边界位移转换关系：

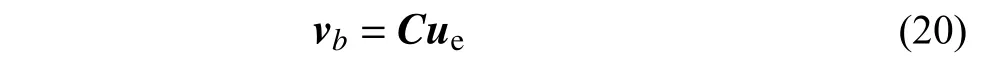
式中，C为全局坐标系下子结构的边界转换矩阵：

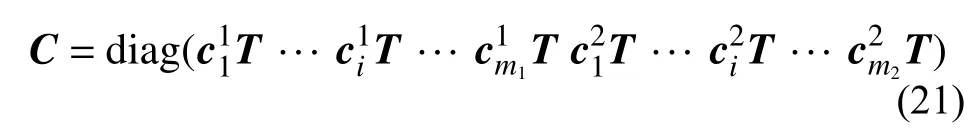
式中，m1和m2分别为第1 和第2 个边界的节点数。

根据主、子结构边界反力所作虚功相等，图3(d)中边界反力之间满足：

将式(20)代入式(22)，得到屈服构件内力re：

再将式(23)代入式(3)，得到屈服构件的非线性修正力=keue-CTqb。

隔离子结构的增量平衡方程可以表示为：

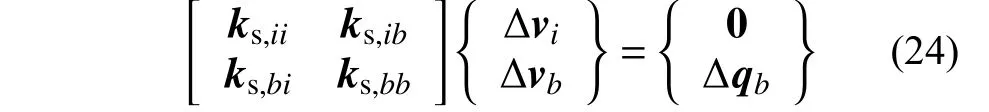
式中：下标i和b分别为隔离子结构内部和边界自由度；ks和q分别为隔离子结构的刚度和外力；Δ为增量。

将式(20)代入式(24)，并将式(24)第二个等式左乘CT，再通过静力凝聚，则有：

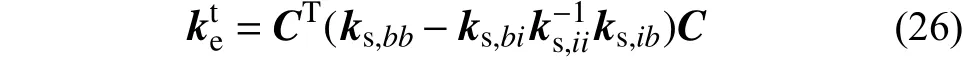
4 分析流程

采用数值子结构方法进行结构地震弹塑性时程分析时，具体分析流程如下：

1)初始化。令n=0、Fn=0 、=0 、=0、Bs,n=0 以及=0。根据式(8)集成等效刚度矩阵K，计算并保存其逆矩阵K-1。根据总时步NS P，得到荷载增量 dF=F/NS P。

2)令n=n+1、i=0、=Bs,n-1以及=，计算当前时步外力Fn=Fn-1+dF，并由式(9)计算得到等效外力Pn。根据式(10)计算得到主结构位移，更新整体结构屈服构件单元状态。若屈服单元数为零，则系统收敛，跳到第7)步；否则，更新布尔矩阵，由式(11)得到塑性自由度位移，进入下一步。

5)根据下式判断塑性自由度系统的收敛性。

5 算例分析

为了验证本文提出的改进的降阶牛顿迭代数值子结构方法(下文简称本文方法)的计算效率和模拟精度，将其与传统的牛顿算法(下文简称传统方法)进行对比分析，同样以上述15 层3 跨的平面钢框架结构为例。为避免平台的差异影响对比分析的客观性，本文算例均在OpenSees 平台中进行，采用BandGeneral 求解器，计算硬件条件是Interl Xeon W-2155CPU，主频是3.3 GHz，内存为64 GB。

5.1 屈服单元隔离非线性分析

进行动力时程分析之前，将竖向重力荷载分10 步逐渐加到结构上。图4 给出8 度和9 度罕遇地震作用下整体结构中隔离单元占比时程曲线。从图4 中可以看出，结构最终屈服单元数占比分别是4.4%和9.6%；8 度罕遇地震作用下，1.62 s时刻结构进入弹塑性状态，直到12 s 左右屈服单元数达到最大；9 度罕遇地震作用下，1.46 s 时刻进入屈服状态，直到12 s 左右塑性区不再扩展。

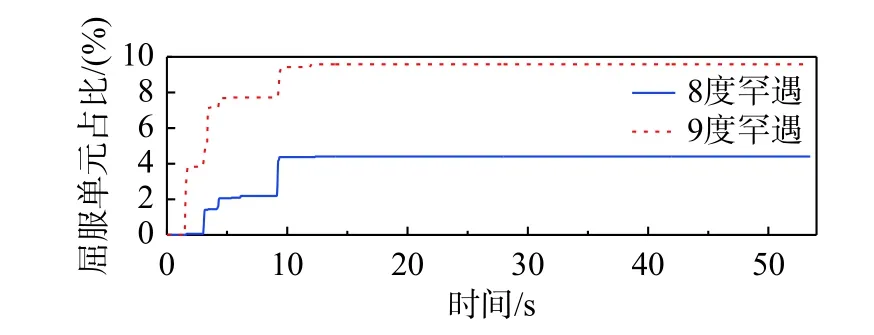
图4 隔离单元所占比例时程曲线Fig. 4 Isolated element percentage time-history curves

图5 给出该平面钢结构在8 度和9 度罕遇地震作用下的塑性区发展历程及大小，图中数值1～6 表示有1 个～6 个屈服单元。由图5 可知，8 度罕遇地震下，1 层～4 层梁端先进入屈服状态，随后，5 层～9 层梁端出现塑性区，其中，1 层～4 层梁端塑性区面积较大；9 度罕遇地震下，1 层～6 层梁端先进入屈服状态，然后，7 层～11 层梁端和底层柱端出现塑性区，其中，1 层～5 层梁端塑性区扩展面积较大，底层柱端塑性区面积相对较小。

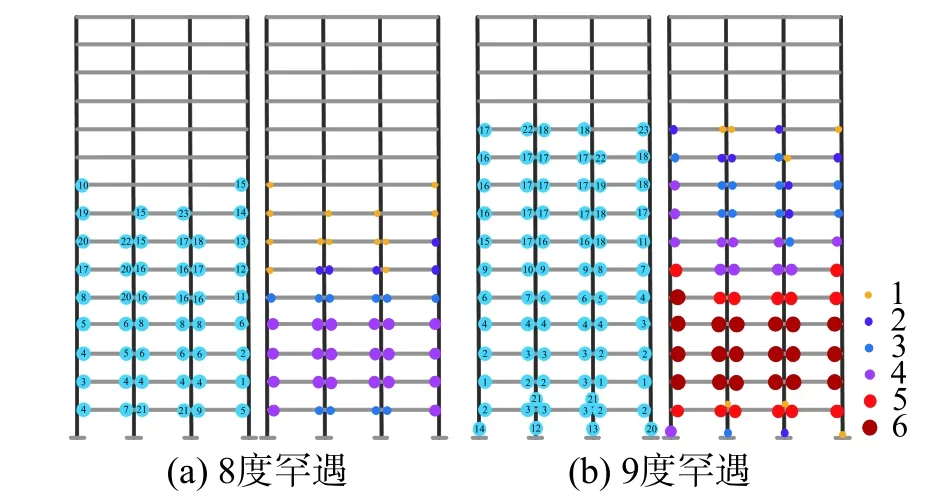
图5 塑性区发展历程及大小Fig. 5 Development history and size of plastic zone

5.2 准确性和可靠性分析

作为对比，采用传统方法分析时，该结构梁柱构件同样划分30 个非线性纤维梁单元。传统方法和本文方法得到的结构顶点位移和基底剪力时程曲线如图6～图9 所示，可以看出，两种方法的计算结果几乎一致。

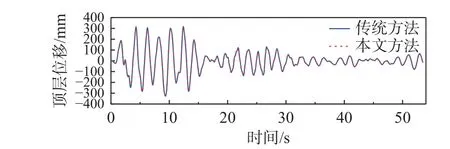
图6 8 度罕遇地震钢结构顶层位移时程曲线Fig. 6 Time-history curves of top displacement for the steel structure under 8 degree rare earthquakes

图7 9 度罕遇地震钢结构顶层位移时程曲线Fig. 7 Time-history curves of top displacement for the steel structure under 9 degree rare earthquakes

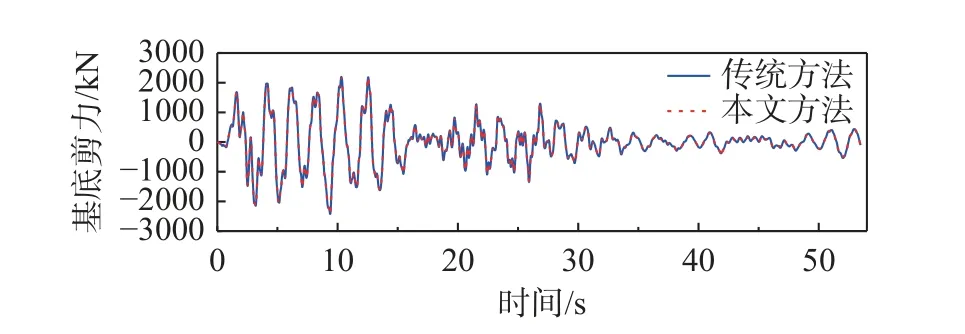
图8 8 度罕遇地震钢结构基底剪力时程曲线Fig. 8 Time-history curves of base reaction for the steelstructure under 8 degree rare earthquakes

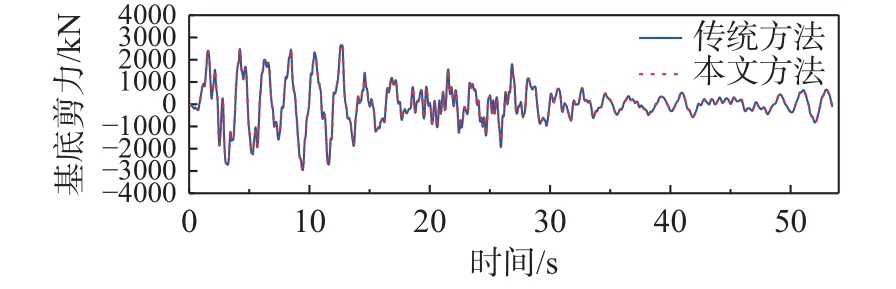
图9 9 度罕遇地震钢结构基底剪力时程曲线Fig. 9 Time-history curves of base reaction for the steelstructure under 9 degree rare earthquakes

进一步，表2 对比两种方法的最大顶点位移和最大基底剪力以及它们的相对误差。由表2 可知，8 度和9 度罕遇地震作用下，结构最大顶层位移和基底剪力的相对误差均不超过0.2%。由式(28)计算得到顶层位移时程曲线的均方差分别为0.14%和0.04%，基底剪力时程曲线的均方差分别为0.02%和0.01%。进一步验证了本文方法的准确性、可靠性。

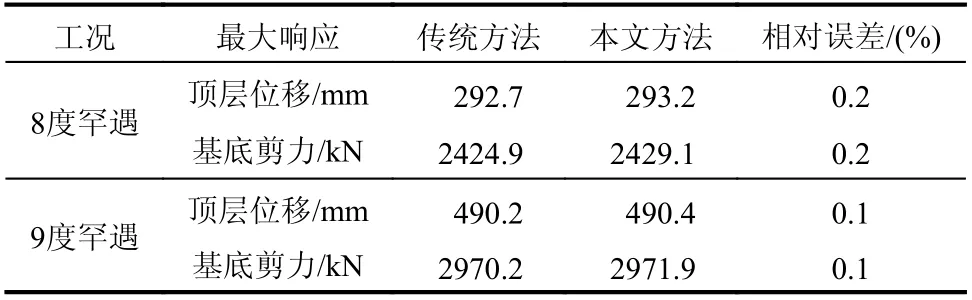
表2 传统方法与本文方法的误差Table 2 Errors using the traditional and proposed methods

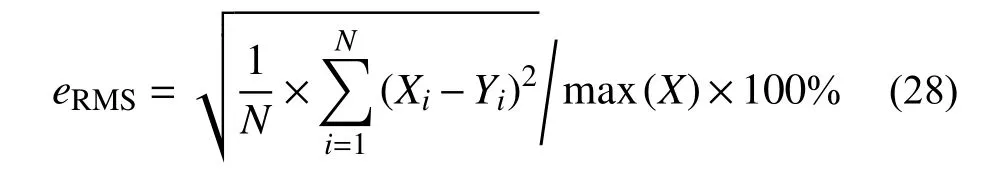
式中：N为总数据量；Xi和Yi为第i时刻响应值。

5.3 计算效率分析

8 度和9 度罕遇地震作用下，传统方法和本文方法的迭代次数时程曲线分别如图10 和图11 所示。此外，传统方法、本文方法以及不动点迭代数值子结构方法(简称原方法)的计算信息如表3所示。由图10 和图11 可知，本文方法的迭代收敛次数略高于传统方法，当地震荷载水平增大或迭代收敛误差减小，本文方法的迭代收敛次数变化较小。由表3 可以看出，当收敛误差为1.0×10-5mm时，8 度和9 度罕遇地震作用下，传统方法最多分别需要4 步和5 步收敛，平均迭代次数分别为2.7和3.1，本文方法最多分别需要6 步和7 步收敛，平均迭代次数分别为3.2 和3.7，而原方法最多分别需要24 步和26 步收敛，平均迭代次数分别为4.6和6.9；当收敛误差为1.0×10-8mm 时，8 度和9 度罕遇地震作用下，传统方法最多分别需要5 步和6 步收敛，平均迭代次数分别为3.2 和3.5，本文方法最多分别需要6 步和7 步收敛，平均迭代次数分别为3.9 和4.1，而原方法最多分别需要41 步和44 步收敛，平均迭代次数分别为7.1 和11.1。由此可见，本文方法所需的荷载步最大收敛次数和平均迭代次数略大于传统方法，但明显小于文献[10 - 13]中的不动点迭代数值子结构方法。

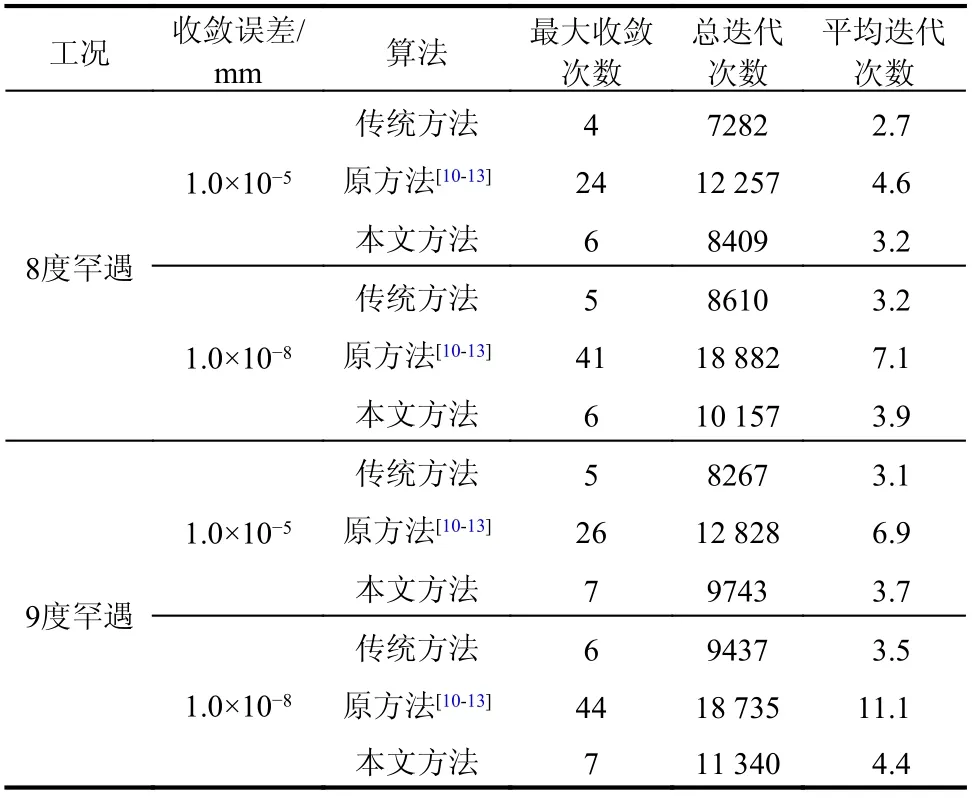
表3 不同方法迭代信息统计表Table 3 Table of iteration information using various methods

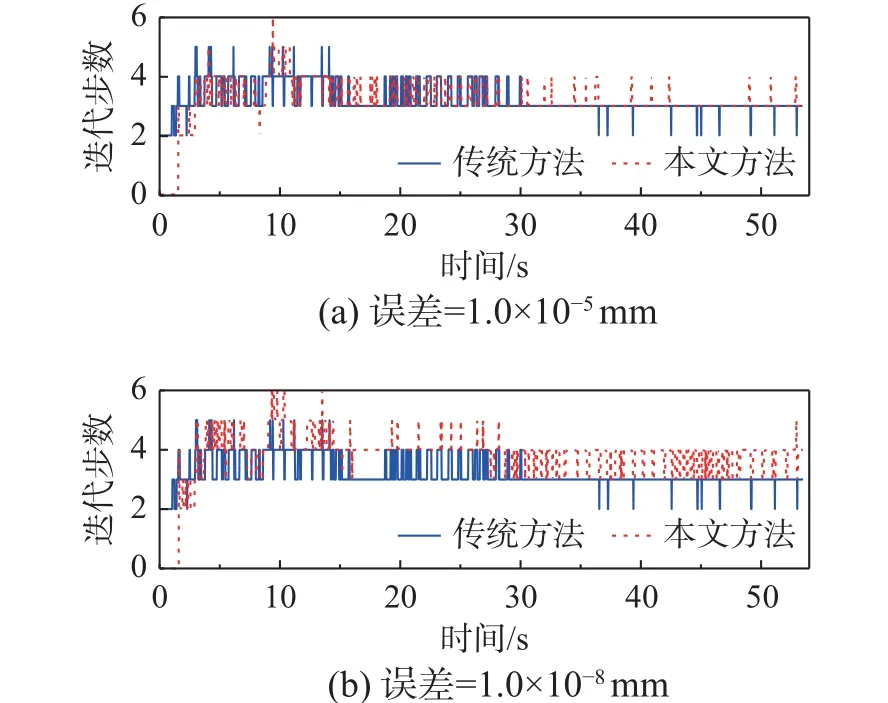
图10 8 度罕遇地震迭代步数时程曲线Fig. 10 Iteration number time-history curves under an 8-degree rare earthquake

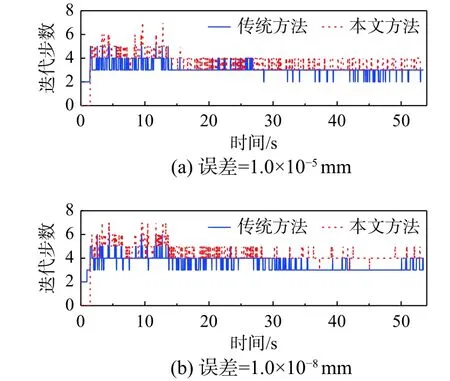
图11 9 度罕遇地震迭代步数时程曲线Fig. 11 Iteration number time-history curves under a 9-degree rare earthquake

当收敛误差为1.0×10-5mm 时，8 度和9 度罕遇地震下传统方法和本文方法的计算信息统计表如表4 所示。可以看出：传统方法分别需要对整体结构刚度K进行7282 次和8267 次集成和分解，计算耗时分别为313 min 和398 min，而本文方法只需在初始化过程中进行一次集成和分解，非线性分析过程中仅需对Hs矩阵进行8409 次和9743 次集成和分解，计算耗时分别为157 min和332 min。

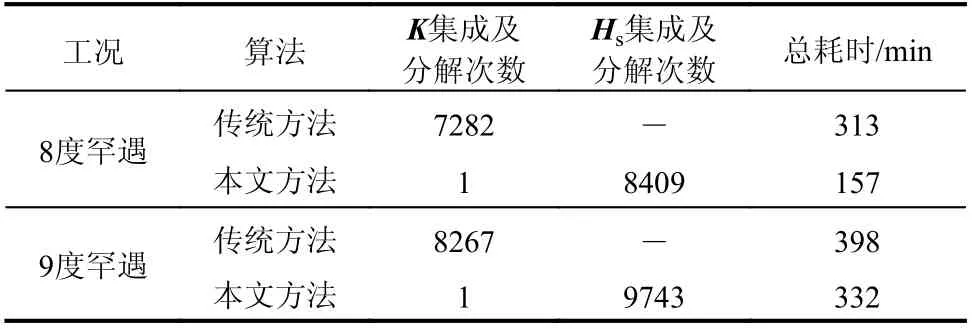
表4 传统方法与本文方法的计算信息统计表Table 4 Computation information using the traditional and proposed methods

图12 给出了传统方法和本文方法求解矩阵维数的时程曲线。从图12 可以看出：随着地震荷载水平的增大，塑性自由度增多，迭代更新和分解的Hs矩阵规模变大；8 度和9 度罕遇地震下，本文方法求解的最大Hs矩阵的维数分别为666 和1713，而传统方法求解的K矩阵维数高达9315。由此可见，结构非线性程度越低，本文方法求解的Hs矩阵规模越小，计算效率越高。

图12 矩阵运算规模时程曲线Fig. 12 Matrix operation size time-history curves

基于变刚度的传统方法需要重复集成和分解整体结构的刚度矩阵K，以及更新所有构件单元的状态，而采用本文方法进行非线性分析时，仅对刚度矩阵K进行一次运算，迭代过程中只更新规模较小的Hs矩阵，且只对数量较少的屈服构件单元进行状态更新。可以推测，针对局部非线性的大规模结构系统的弹塑性分析，本文方法较传统方法具有显著的计算优势。