水力耦合下节理砂岩三轴压缩渗透性能试验研究
2022-07-30王福奇李治祥经来旺高
王福奇 李治祥 吴 军 田 斌 经来旺高 聪
(1.华亭煤业大柳煤矿有限公司,甘肃 华亭 744100;2.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001;3.安徽理工大学 力学与光电物理学院,安徽 淮南 232001)
0 引 言
随着煤炭资源开采不断向深部发展,岩石三轴压缩渗透性能已成为学者们关注的热点[1-3]。深部高地应力、高水压耦合环境下,岩石受力变形特性将发生极大改变,渗流场与应力场耦合作用将进一步加速岩体性能劣化[4-5],直接影响到地下工程安全。薛俊华等[6]通过稳态法测试获得了煤岩全应力-应变过程各阶段渗透率及其峰值强度,有助于对采动荷载影响下煤岩渗流-应力耦合性能的理解;赵延林等[7]采用瞬态法针对茅口灰岩开展三轴压缩渗透试验,得到了不同围压、渗透水压下灰岩渗透性、峰值强度以及变形性能;王伟等[8]采用达西定律计算出花岗岩三轴压缩过程各阶段渗透率值,明确了不同围压和渗透压组合下花岗岩渗透特性以及力学特性。然而,由于岩石类别不同,内部组成结构存在差异,使得三轴压缩渗透性能未能按照某种特定方式统一发展。许江等针对砂岩在三轴排水状态下峰值破坏强度、有效峰值破坏强度、有效剪切强度以及有效正应力展开研究,但是关于渗透率演化分析尚未涉及[9]。此外,节理砂岩在煤矿采掘过程中属于常见岩体,节理的存在是应力释放或应力集中的关键构造[10],将直接影响到工程岩体的稳定。因此,笔者以节理砂岩作为研究对象,针对其所处的高地应力、高水压环境,开展围压渗透水压耦合作用下的三轴压缩渗透试验,研究水力耦合条件下节理砂岩的受力变形特性,分析应力状态改变对渗透率的影响规律。
1 试验方案
本试验采用的节理砂岩取自于甘肃华亭煤业大柳煤矿。首先将现场取回的岩块加工成ϕ50 mm×100 mm 的圆柱体试件[11],再通过声波测速仪挑选出波速相近的试件,以排除三轴压缩渗透过程因试件差异性对试验结果造成的干扰,图1为正式开展试验时所需用到的部分节理砂岩试样。

图1 部分节理砂岩试样
采用TAW-2000岩石伺服试验机,配有三套独立的加载系统:轴压加载系统、围压加载系统、孔隙水压加载系统。三轴压缩渗透试验步骤如下:①将饱水节理砂岩试件采用热缩橡胶套密封后安装在试验机底座上;②轴向施加1 k N 荷载固定试件,再向三轴腔内施加围压,当围压施加至设计值后保持不变;③在试件上端施加渗透水压,下端与大气压相通以此形成渗透压差;④渗透水压施加至设计值后保持不变,并维持该状态30 min;⑤采用一定的加载速率施加轴向荷载直至试件破坏,整个加载过程需要3~4 h。节理砂岩三轴压缩渗透过程受力示意如图2所示。在试验过程中,数据采集器自动记录荷载、位移、水流量等数据,根据岩样所处地应力环境设计围压水平分别为10 MPa、15 MPa,渗透水压水平分别为1 MPa、4 MPa、8 MPa。试件编号命名方式以C10P1为例:C10表示围压10 MPa,P1表示渗透水压1 MPa,以此类推。
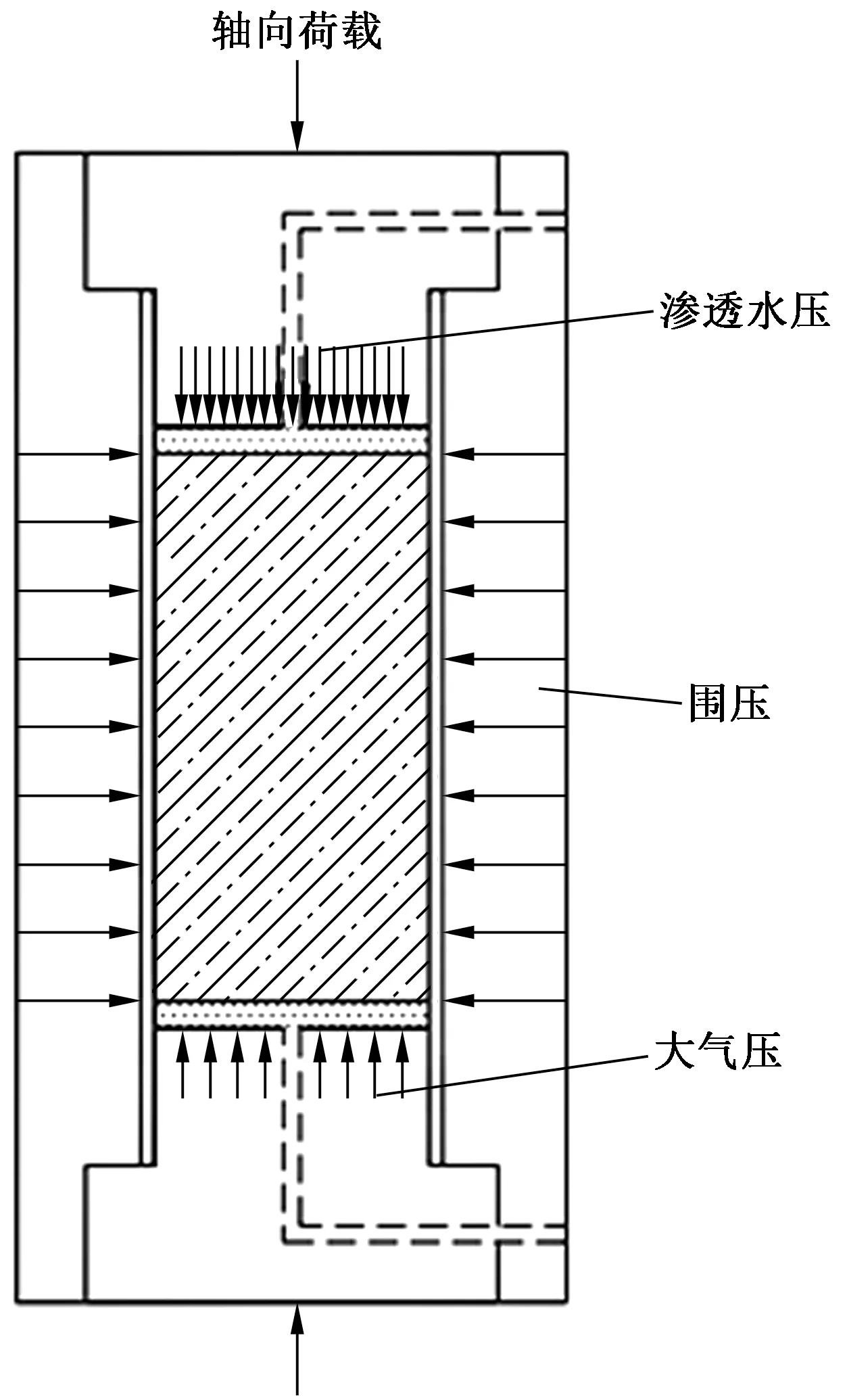
图2 节理砂岩三轴压缩渗透过程受力示意
在节理砂岩三轴压缩渗透过程中,根据水流量变化情况,由达西定律计算得到各测试点渗透率值[12],计算公式如下:

式中,k为渗透率,m2;A为水透过试件横截面面积,m2;p为渗透水压,Pa;L为试件高度,m;Q为水透过试件流量,m3;μ为粘度系数,室温下为1.005×10-3Pa·s。
2 结果分析与讨论
2.1 三轴压缩渗透强度
表1为节理砂岩在不同围压-渗透水压组合下三轴压缩渗透状态峰值强度、初始渗透率、最小渗透率和最大渗透率。从表1可以看出,在相同围压状态下,随着渗透水压增加,峰值强度呈递减趋势,这与三轴压缩渗透过程渗流场和应力场耦合作用相关,渗透水压越大越容易激发节理砂岩内部裂纹的发展,使得孔隙水在试件内部的渗流路径增多,渗流场和应力场耦合作用产生的不利效果愈加明显[13]。不同围压水平下渗透水压由1 MPa依次增加至4 MPa、8 MPa时,峰值强度平均下降15.34%、39.41%,渗透水压增加幅度越高,强度降低越明显。然而,在渗透水压相同围压不同情况下,随着围压升高,峰值强度呈增加趋势,围压作用能够使得试件内部裂纹更加密实,水在试件内部的流动阻力增大,以至于渗流场与应力场耦合作用效应减弱,同时,现有研究表明,围压增加可以有效减缓试件的损伤发展[14]。渗透水压分别在1MPa、4MPa、8MPa时围压由10MPa升高至15MPa,试件峰值强度依次增加了41.63%、38.59%、42.16%。节理砂岩三轴压缩渗透强度对围压的变化更加敏感,且随着围压增加,由渗透水压对试件峰值强度发展构成的威胁逐步降低,渗透水压对试件峰值强度的影响比围压的影响程度弱。
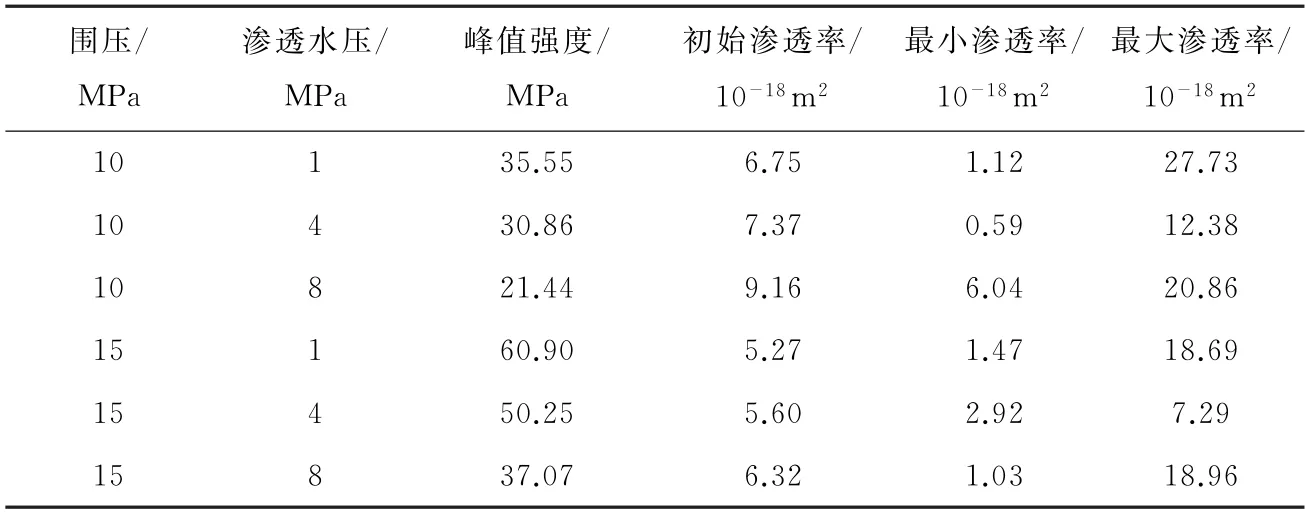
表1 节理砂岩三轴压缩渗透性能指标
2.2 三轴压缩渗透性能
表1中初始渗透率是指在试验开始加载阶段围压、渗透水压分别施加至设计值时,轴向在1 k N 的固定荷载作用下饱水30 min,并根据试样在加载过程中水流量变化的情况测得渗透率。显然,在渗透水压8 MPa时,初始渗透率在相同围压水平下均达到最大,在渗透水压1 MPa时,初始渗透率最低,在本试验中因渗透水压提高,初始渗透率增加幅度为6.26%~35.70%。在初始渗透率测试状态下,由于各组试件事先已采用声波测试排除了差异性影响,故主要区别仅在于渗透水压值。渗透水压值越高,在试件上下端面形成的压力差越大,越有利于孔隙水在试件内部渗流,水流量得到有效增大,致使渗透率提高。相反,在渗透水压偏低时水,在试件内部渗流的动力相对不足,使得相同时间内透过试件的水流量与高渗透水压时相比要低,造成初始渗透率减小。
最小渗透率指的是各测试点中渗透率最低值,围压作用使得试件内部竖向裂纹被压密实,后续轴向荷载开始作用时又使得试件内部横向裂纹被压密实,因此,试件内部渗透通道大幅缩小,致使渗透率降低,渗透率最低点基本分布在变形初始阶段。最大渗透率指的是各测试点中渗透率最大值,随着轴向荷载不断增大,试件内部裂纹由最初压密闭合逐渐转向萌生、扩展、贯通,最终形成宏观裂纹,从而使得水在试件内部渗流速度加快,渗透率得到大幅增加,渗透率最高点位置多分布在试件弹塑性屈服阶段。由于试件三轴压缩渗透加载过程除初始渗透率测试点位置统一外,其他各测试点位置并非固定[15],因此,初始渗透率明显表现出相同围压情况下随着渗透水压增大初始渗透率提高,相同渗透水压情况下随着围压增大初始渗透率降低的特征。最小渗透率和最大渗透率是各测试点中的极值,两者相差一个数量级,其中最小渗透率发生在变形较小的初始加载阶段,最大渗透率发生在峰值应变前试件屈服阶段,由此可见,试件内部裂缝发展联通后渗透率发生了较大改变。
2.3 渗透率-应力演化关系
节理砂岩在不同围压、不同渗透水压下渗透率-应力演化关系如图3所示。加载初期随着应力增加渗透率呈下降趋势,尤其是在图3(a)、图3(d)中渗透率降低至一定值后,便随着应力变化保持相对稳定,待试件进入屈服阶段内部新生裂缝不断得到发展,渗透率开始快速上升,很快达到渗透率最大值。图3(c)中渗透率在应力范围很小时首先随着应力增加而降低,随后渗透率逐步开始上升,但该阶段渗透率上升速率偏慢;由于渗流场-应力场耦合作用使得节理砂岩试件骨架结构弱化[16],应力持续增加达到屈服阶段后渗透率快速上升至最大值,这种情况在图3(b)、图3(f)均有体现,相对而言,图3(c)中渗透率达到最大值位置明显提前,分析认为,这与图3(c)中C10P8组试件所处试验条件有关,该组试件较图3(b)相比渗透水压大一倍,更利于试件内部渗流通道的提前形成,与图3(f)相比围压偏小,对试件内部裂纹的压密作用相对减弱,从而使得水在试件内部渗流阻力减少,更多的压力水进入试件内部,渗流场与应力场耦合作用效果愈加明显,渗透率发展得到提前。观察发现图3(b)、图3(c)、图3(f)中渗透率达到峰值后随着位移的持续增加,渗透率均有小幅回落,说明此时试件受围压作用影响处于塑性压密阶段,但从渗透率降幅来看,试件内部的渗流通道受围压压密闭合程度影响偏低,故仍然具有较好的连通性[17]。本次试验过程中渗透率峰值点位置在试件应力峰值点位置附近有三例,分别是图3(a)、图3(b)、图3(e);渗透率峰值点位置较试件应力峰值点位置提前出现也有三例,分别是图3(c)、图3(d)、图3(f),提前位置多集中在应力屈服阶段。
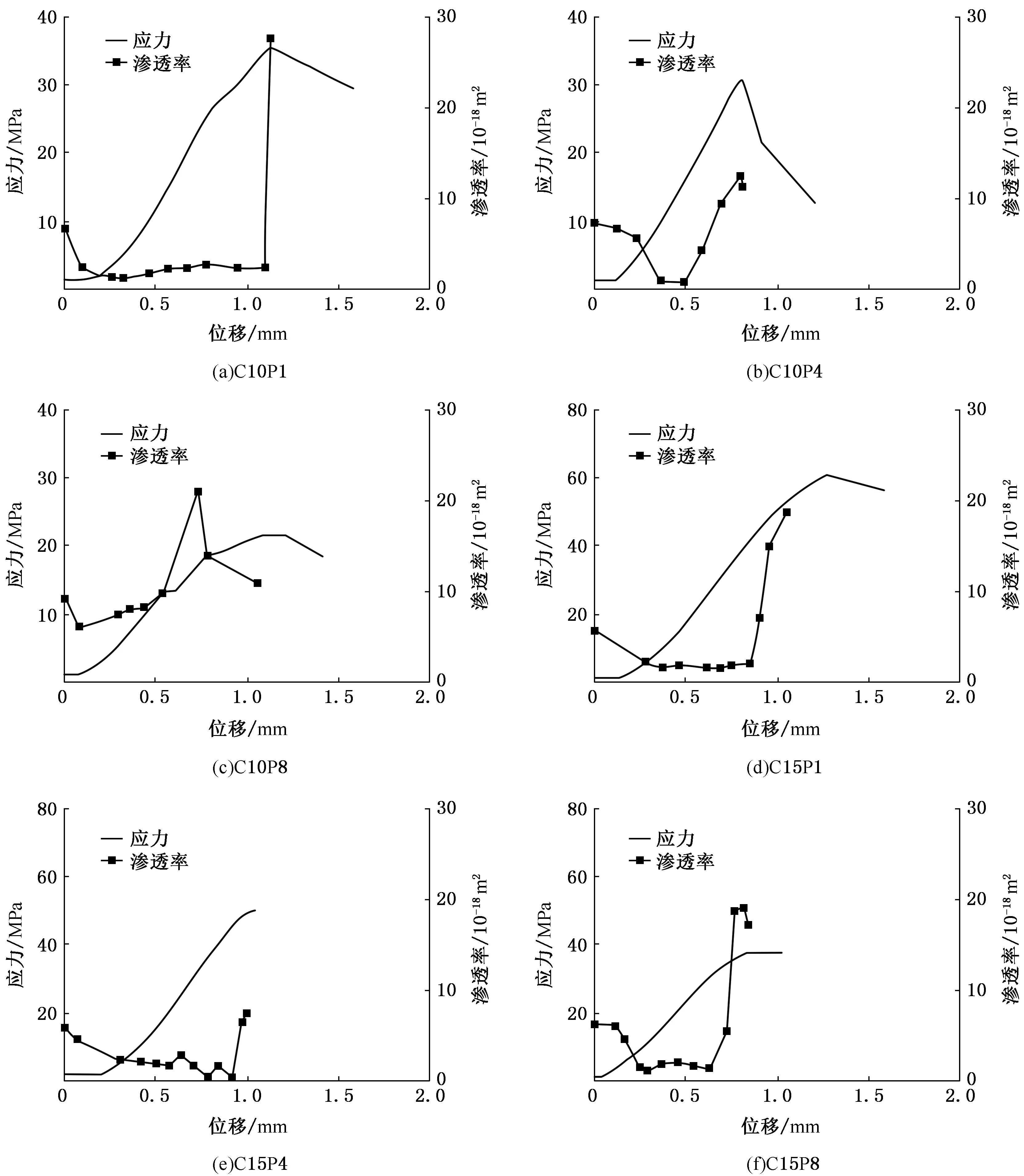
图3 节理砂岩渗透率-应力演化关系
2.4 三轴压缩破坏形态
在三轴压缩渗透状态下,节理砂岩破坏时宏观贯通裂纹基本上是沿着节理面形成,这是因为节理面在加载过程中极易产生应力集中,当试件中最薄弱的节理面发生斜剪断裂后,承载力便随着变形的持续增加表现出降低趋势,部分试件因薄弱面分布较多破坏程度还将加剧。由此可见,针对节理砂岩而言节理面的存在导致岩石强度降低,尤其是在高地应力、高水压环境中,在节理面处更容易形成贯通的渗透水通道,加速岩土渗流场与应力场之间的相互耦合作用,对节理砂岩地层稳定性的劣化影响更显著。
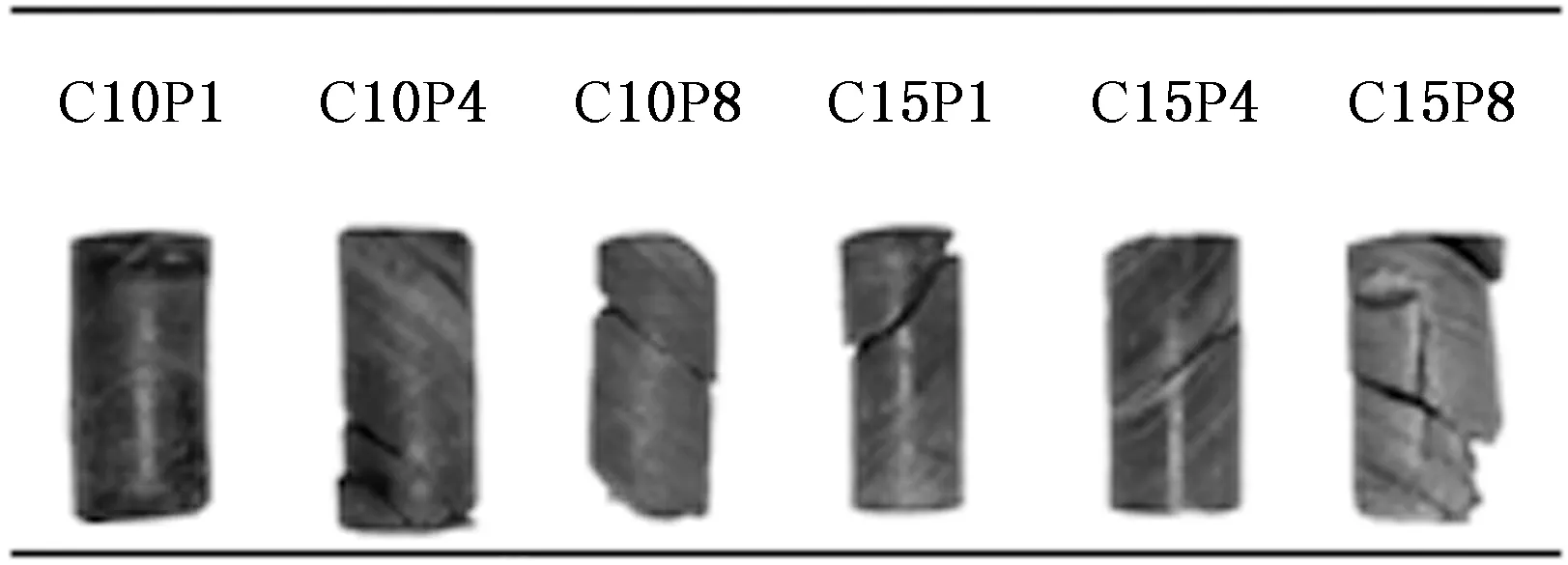
图4 节理砂岩三轴压缩渗透破坏形态
3 结 论
(1)三轴压缩渗透试验表明节理砂岩峰值强度、初始渗透率与围压、渗透水压存在密切联系。随着围压增大,峰值强度提高、初始渗透率降低;随着渗透水压增大,峰值强度降低、初始渗透率提高。
(2)受初始荷载压密作用影响,节理砂岩渗透率前期表现出明显下降的趋势,随后进入弹性阶段渗透率保持相对稳定发展状态,当应力达到屈服阶段后,试件内部裂缝得到发展连通致使渗透率快速上升。
(3)三轴压缩渗透破坏时基本上是沿着节理面先断裂,最终试件发生斜剪破坏,节理面多的试件破坏程度更加明显。
