光子晶体多组元缺陷态问题研究

王立群，严佳新，卢 欣,石丽伟,张肖利

(1.中国石油大学(北京)理学院，北京 102249；2.中国政法大学法治信息管理学院，北京 102249)

0 引 言

光子晶体又称光子晶格材料或光子带隙材料，是一种介电常数呈周期性变化的人造光学材料。Yablonovitch[1]和John[2]于1987年分别提出光子晶体的概念，他们认为光子晶体的周期性结构特性是可以产生带结构的，在此之后人们对光子晶体产生了浓厚的兴趣。光子带隙也称禁带，是指由于受到布拉格散射的影响，在某一范围内波不能在任何方向上通过晶体传播。禁带频率范围之外的称为通带。光子带隙有许多重要的物理性质，例如自发发射抑制[1]、稳定的孤立波[3-4]和在边缘附近自发发射的非指数衰减[5-6]等。光子晶体另一个主要特性是当破坏了其周期性介电结构时，在带隙频率区域可能会出现局部缺陷模式[7-9]。一般是通过引入点缺陷或者线缺陷来破坏其周期性结构。在设计点缺陷时，波将聚集在微米量级区域中形成微腔[10]，由于介电常数不连续所产生的反射、散射和衍射使得光在很小的区域中来回振荡。当设计线缺陷时，会使之前处于某一禁带范围内的波开始传播。于是，基于以上光子晶体的局域性特征，衍生出来很多有价值的应用，比如将线缺陷引入到常规光子晶体中的光波导。光子带隙的存在使拐角无损耗传播得以实现，这个特性对光学微电路非常有用[11]。再如，由于光的偏振而通常具有高品质因数并会显示出较窄的透射光谱，因此它们可以用作良好的谐振器、偏振器、滤光器、光子晶体光纤[12-13]和光子晶体激光器[14-18]。研究光子晶体缺陷态问题有很多方法，平面波展开法[9,19-20]、多重散射法[21]、时域有限差分法[22-24]等均可以有效处理二维光子晶体缺陷态问题。但是由于平面波展开法的收敛性较慢，超晶胞的尺寸通常被限制在一个较小的值，所以数值结果会受到影响。多重散射法和时域有限差分法在处理复杂介质形状时会有一定的局限性。PG有限元界面问题计算方法(Petrov-Galerkin finite element interface method， PGFEIM)是一种算法简单、拓展性强的界面问题求解方法，适用于各类带有复杂界面的多物理场问题的计算。因此，将PGFEIM应用于求解带有周期边界条件的椭圆方程和弹性方程的界面问题以及2D声子晶体问题的计算[25]，并将其拓展到向量有限元形式，解决了含各向异性夹杂物、压电材料，以及纳米压电材料的声子晶体问题[26]，计算了各向异性光子晶体的能带结构[27]。本文将首次在PGFEIM的研究体系下引入超胞以解决缺陷态的光子晶体问题，包括多组元的缺陷态问题和各向异性光子晶体的缺陷态问题等。

1 问题描述

本文中，光在二维光子晶体中传播的控制方程为时间谐波麦克斯韦方程组:

(1)

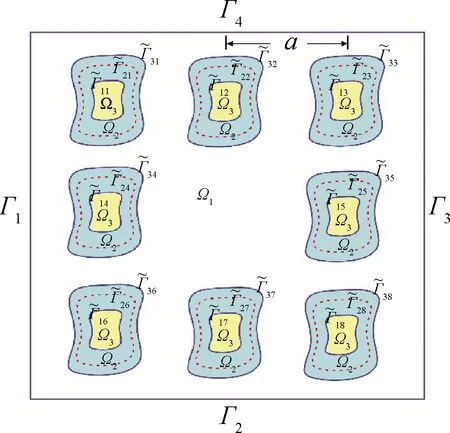
图1 具有点缺陷的三组元光子晶体3×3超胞示意图Fig.1 Three-component photonic crystal 3×3 supercell with point defects

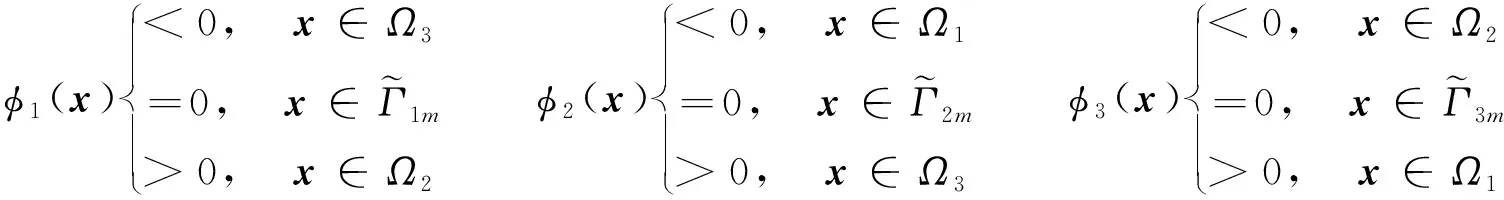
(2)

本文假设μ=1，介电常数ε是周期性函数ε(x+a)=ε(x)并满足

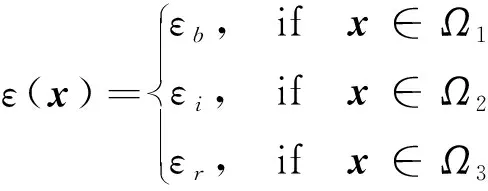
(3)

式中：εr，εi和εb代表每个组元的介电常数，a=i1a1+i2a2表示实空间中的晶格平移向量，(i1,i2)∈2，a1和a2是晶格的基向量。对于各向同性介质而言，ε是标量。对于各向异性介质而言，

为了方便表示，假设介质是横向各向异性，ε13=ε23=ε31=ε32=0。

在二维光子晶体问题中，麦克斯韦方程(1)可以被解耦成横磁波(TM模)和横电波(TE模)。对于TM模，电场和磁场可以分别表示为：E=(0,0,Ez)和H=(Hx,Hy,0)。

然后麦克斯韦方程可以写成：

(4)

(5)

(6)

将式(4)和(5)代入式(6)中，可以得到TM模的控制方程：

(7)

对于TE模, 电场和磁场分别为E=(Ex,Ey,0)和H=(0,0,Hz)。因此，麦克斯韦方程(1)可以表示为：

(8)

(9)

(10)

消去式(9)和式(10)中的Ex有：

(11)

同样地，消去式(9)和式(10)中的Ey有：

(12)

将式(11)和式(12)代入式(8)，得到TE模的控制方程为：

(13)

重新整理式(7)和式(13)为：

ΔEz+κ2βEz=0

(14)

(15)

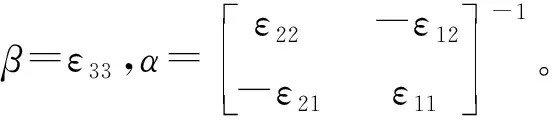
(16)

由于光子晶体具有周期性的几何结构，根据Bloch定理，对于如图2所示的超胞和第一布里渊区，其边界条件可表示为：

图2 周期性边界条件与第一布里渊区Fig.2 Periodic boundary conditions and the first Brillouin zone

u(xΓ3)=ζu(xΓ1)T(xΓ3)=ζT(xΓ1)
u(xΓ4)=τu(xΓ2)T(xΓ4)=τT(xΓ2)

(17)

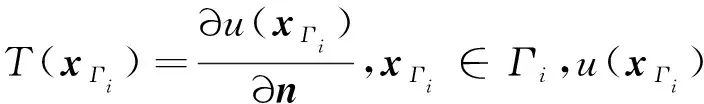
2 弱形式

为了有效处理 Bloch边界条件，在进行弱形式推导前先定义测试函数空间：

(18)

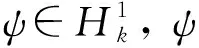
(19)

式中αi和βi由区域Ωi上的材料决定。

由Bloch边界条件(17)和测试函数(18)的定义可得：

(20)

综合以上可得到弱形式：

(21)

3 数值方法

图3 方形晶格的网格划分Fig.3 Square lattice meshing

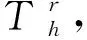
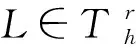
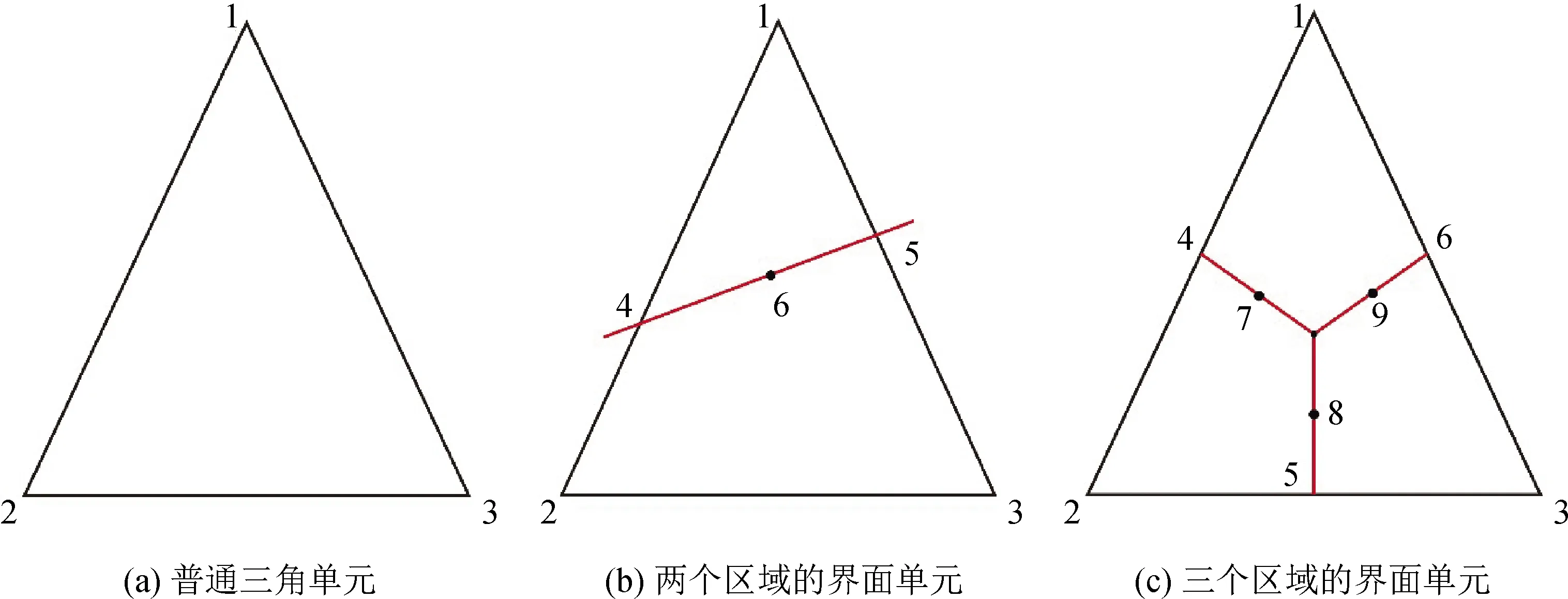
图4 三种三角形形态Fig.4 Three triangle states

为了有效地处理Bloch边界条件，需要在非贴体网格系统的基础上创建非贴体投影网格。如图5所示，将右、上边界的单元格投影到左、下边界，以对应的关联点为中心组成积分单元。投影后，无边界点和内点之分，极大地简化了Bloch 边界条件的处理过程，降低了计算的难度，减少了计算的时间。

图5 方形晶格的投影网格Fig.5 Projection grid of square lattice

由于数值离散的需要，建立以下两个离散空间：

H1,h={ψh=(ψ(xjl)):0≤j≤Js,0≤l≤Ls}

(22)

(23)

式中，ψ(xjl)代表ψ(x)在x=xjl处的值。同理，ψ(xv)是ψ(x)在x=xv处的值。

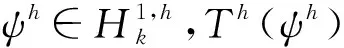
由以上定义可得以下定理：

定理对于所有的uh∈H1,h，给定Th和φl，Uh(uh)可以唯一确定。

证明：参见文献[25]。

为简便起见，定义

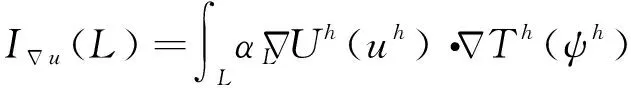
(24)

式中，αL和βL代表L所在区域的材料参数，可得PGFEIM的数值离散形式：

方法 确定κ2∈及uh∈H1,h，所以对于所有有：

(25)

所有系数可以组装到矩阵中，于是有矩阵形式：

AU=κ2BU

(26)

式中:U为数值解，取值波矢向量k便可求出对应的κ。

4 数值算例与分析

本节将采用PGFEIM进行光子晶体缺陷态的数值计算与结果分析。通过研究不同组元体系、不同介质柱形状以及不同缺陷位置的光子晶体，揭示影响能带结构变化的因素。

4.1 二组元数值算例与分析

为了验证算法的有效性，本文将与参考文献[28]中的结果进行比较，同时通过变换不同的缺陷位置，观察不同的缺陷态结构对能带结构的影响。在二组元算例中考虑的是各向同性的介质，折射率n2=3.4，介质柱半径r=0.3，背景材料的折射率n1=1，晶格常数α为1。填充率与文献[28]中相同。

图6展示的是无缺陷TM模与TE模的数值结果。TM模里有两条很宽的禁带，范围分别是0.237 3～0.309 1及0.426 8～0.532 6，而TE模中并无禁带产生。

图6 完美超胞的能带结构图Fig.6 Band structure diagram of a perfect supercell

图7展示的是点缺陷的数值结果。图7(a)展示的是超胞的几何结构，图7(b)和图7(c)分别展示了TM模和TE模的数值结果。在图7(b)中，(1)为一个点缺陷所形成的能带结构，原本的禁带范围内产生了一条缺陷带。也就是说，通过引入一个缺陷破坏了晶体的周期性结构，使得在频率0.474 4～0.477 1内产生允带。(2)是使两个相邻的散射体消失，第一禁带产生一条频率范围是0.294 6～0.300 6的缺陷带，第二禁带产生了两条缺陷带。(3)中第一禁带的缺陷带消失了，第二禁带的两条缺陷带逐渐靠近。(4)中缺陷带宽度为0.007 5和0.007 2，相较于(3)中的0.004 2和0.000 2明显变宽。而对于TE模来说，引入点缺陷增加了一些比较窄的禁带。

图7 点缺陷与多个点缺陷耦合的能带结构Fig.7 Band structures with point defects and coupling of multiple point defects

如图8所示，(1)为通过移除最中间一列的散射体得到的线缺陷，TM模中可以明显看出第二禁带消失以及相应地第一禁带也变窄，线缺陷使得在原本禁止频率范围内的光波可以继续沿着该频率段传播，这也就是光波导。(2)是在完美线缺陷中耦合一个微腔，可以看到禁带范围变大，并且打开了几条窄带。(3)中进一步增加了点缺陷数量，不仅有一条完整线缺陷，还另外移除了8个散射体，所以其带隙变化较大。(4)与(2)的不同之处在于点缺陷靠近线缺陷，产生了多条禁带，这可能是点缺陷与线缺陷同时产生作用的结果。

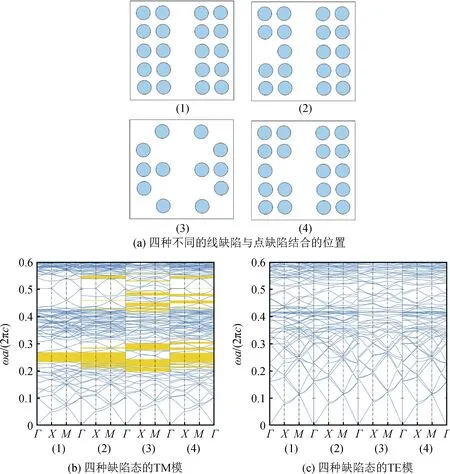
图8 线缺陷与点线耦合缺陷的能带结构Fig.8 Band structure of line defects and point coupled with line defects

通过以上对比可以发现，引入点缺陷只是局限的使得某一小范围内的波继续传播，产生一条缺陷带，或者耦合多个点缺陷使得一些特定范围内的波可以传播；而线缺陷所产生的影响较大，可以使得整个禁带消失。当线缺陷与点缺陷结合起来，波导结构中的侧点缺陷可以有效地用于光子晶体的阻带内诱导窄通带或在波导的通带内诱导非常窄的阻带。

4.2 三组元数值算例与分析

本小节将使用 PGFEIM 算法计算光子晶体缺陷态问题下的三组元结构，同时引入不均匀介质，例如液晶 (liquid crystal， LC)和碲 (tellurium， Te)。一般 LC 有两种折射率，正常折射率和异常折射率。介电张量的分量如下[27,29]：

(27)

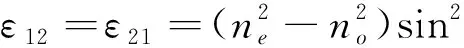
(28)

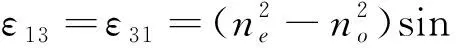
(29)

(30)

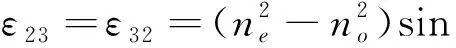
(31)

(32)

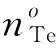
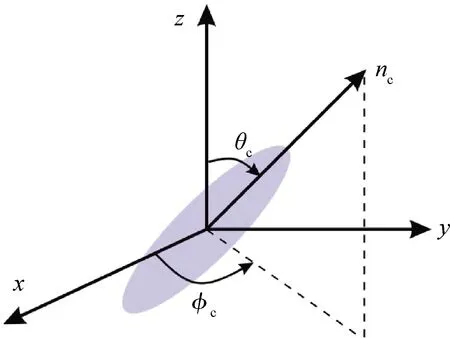
图9 LC的θc、φc和nc的定义Fig.9 Definition of θc, φc and nc for LC

下面考虑复杂介质形状，并且观察直线型、n型和v型缺陷的能带结构差异。如图10所示，介质形状分别为：(1)三角形 Te 包裹圆形 LC 介质置于空气中；(2)圆形 Te 包裹三角形LC介质置于空气中；(3)四角星 Te 包裹圆形 LC 介质置于空气中；(4)圆形 Te 包裹四角星 LC 介质置于空气中。

图10 三组元光子晶体的几种复杂缺陷情形Fig.10 Several complex defect situations of three-component photonic crystal

在图11中，直线型缺陷态 TM 模中基本都有两条相对较宽的禁带，(3)中第二禁带较窄且高频区域出现了一些窄带，而 TE 模只有一些窄带；v型缺陷态 TM 模中(3)出现了三条较宽的禁带且 TE 模在四种形状介质中均产生了多条禁带。以(2)和(4)的结果来看，Ω3区域的介质形状对结果影响比较有限。以(1)和(3)的结果来看，表面层越是不光滑第二禁带越窄。纵向来看，n型缺陷态 TM 模中的高频区域更容易产生禁带，且对于TE 模来说n型与v型的缺陷态更容易产生禁带。

图11 三组元复杂缺陷态的能带结构图。(1)～(4)列分别与图10中(1)～(4)的散射体形状对应。由上至下1～3行分别对应图10中(a)～(c)三种缺陷态Fig.11 Band structure of three-component photonic crystals with complex defect states. Columns (1)～(4) correspond to the scatterer shapes (1)～(4) in Fig. 10, respectively. Lines 1～3 from top to bottom correspond to defects (a)～(c) in Fig. 10, respectively

5 结 论

本文将单胞拓展为超胞，使用 PGFEIM 算法来计算二维光子晶体缺陷态问题。考虑了 TM 模与 TE模，在二组元情况中考察了多种点缺陷与线缺陷结合的能带结构，为光波调制及滤波器的制作等应用提供了更多方法与方向，对于三组元的研究更加拓展了光学器件制作的思路。由本文研究结果可以发现，PGFEIM 算法在研究多组元问题上十分有效，为进一步的光子晶体计算研究打下了基础。