低碳经济下企业碳排放与经济发展的关联实证分析——以云南昆钢嘉华水泥建材有限公司为例

梁琴 李锐

（1.云南林业职业技术学院,云南 昆明 650224；2.昆明钢铁控股有限公司,云南 昆明 650224）

20世纪末，《京都议定书》发布，明确了发达国家和发展中国家具体应承担的减排降碳责任。我国政府将节能减排作为发展战略之一，在2009年，国务院指出截至2020年，中国碳排放总量与2005年相比下降了40%。在此期间，我国能源消耗总量和速度首次超越美国。相较于发达国家，我国能源消耗对国民总值的提升贡献值较低，中国面临着严重的环境压力。基于此，在提高我国经济增长速度的同时，如何降低碳排放总量成为关注的重点。在我国，碳排放主要源于能源业、建筑业、工业以及森林建设，尤其是工业占碳排放总量较大。因此，本文在低碳经济背景下，以云南昆钢嘉华水泥建材有限公司（以下简称昆钢嘉华公司）为研究对象，运用Eviews软件分析其碳排放与经济发展的关联，同时分析影响碳排放的因素，旨在推动公司实现减排目标和绿色发展。

1 文献综述

在研究碳排放和经济发展之间的关系时，笔者发现，环境库兹涅茨曲线（EKC）在该研究中运用得最为普遍。国外文献如 Grossman（1995）在研究中选取了北美作为研究对象，经过分析发现，人均收入、环境质量双方间存在显著的倒U型曲线形式，其在研究结论中指出环境质量受经济增长的影响较大[1]；Panayotou（1993）是提出环境库兹涅茨曲线（EKC）的第一人[2]。EKC被提出后，发展迅速，业界针对该理论的研究逐渐增多。Narayan（2010）以43个发展中国家为研究对象，在分析这些国家碳排放量和人均收入数据的基础上发现，只有15个发展中国家与EKC倒U型曲线贴近[3]。所以，本研究在探究EKC 曲线和 Tapio 脱钩模型理论的背景下，选取昆钢嘉华公司为研究对象，对其碳排放和经济增长进行了脱钩分析，同时运用IPAT模型分析了影响公司碳排放的因素[4]。研究最后提出了针对昆钢嘉华公司节能减排的具体对策，以期为相关企业提供理论借鉴，为社会实现减排目标作出贡献。

2 实证检验及数据分析

2.1 碳排放计算与数据的选取

研究以真实数据和现实情况为基础，以提高研究方案的可行性，在能源耗量估算法的基础上运用综合方面测量二氧化碳排放总量，详细的过程如式（1）：

基于式（1），A代表碳排放总量；Bi为能源i以标煤为计量单位的消费量；Ci为能源i的碳排放系数，其中，碳排放系数源于日本能源经济研究所。

整理与总结昆钢嘉华公司能源消费量数据，掌握了公司2010—2021 年二氧化碳排放量。

2.2 模型构建

2.2.1 EKC 模型

研究发现，在研究环境变化趋势中，线性模型和对数性模型运用最为普遍，在这两种模型下，可以衍生出一条关于收入的多项式函数，本研究构建的环境库兹涅兹曲线（EKC）函数具体如式（2）：

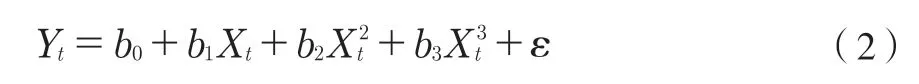
在式（2）中，Y代表人均二氧化碳排放，t代表年，X代表人均 GDP；b0、b1、b2、b3分别是解释变量的系数，ε代表随机误差项。

2.2.2 脱钩模型

根据图表1了解到，Tapio（2005）将研究范围放在欧盟成员国上，在计算这些国家和地区碳排放量时综合运用了物质消耗弹性脱钩评价法和弹性值，首次测量了能源消耗、GDP间的具体弹性值，具体如式（3）；计算二氧化碳和能源消耗二者间的具体弹性值，如式（4），将二者进行乘积，进而计算二氧化碳和GDP间的具体弹性值，如式（5），也就是脱钩指数。

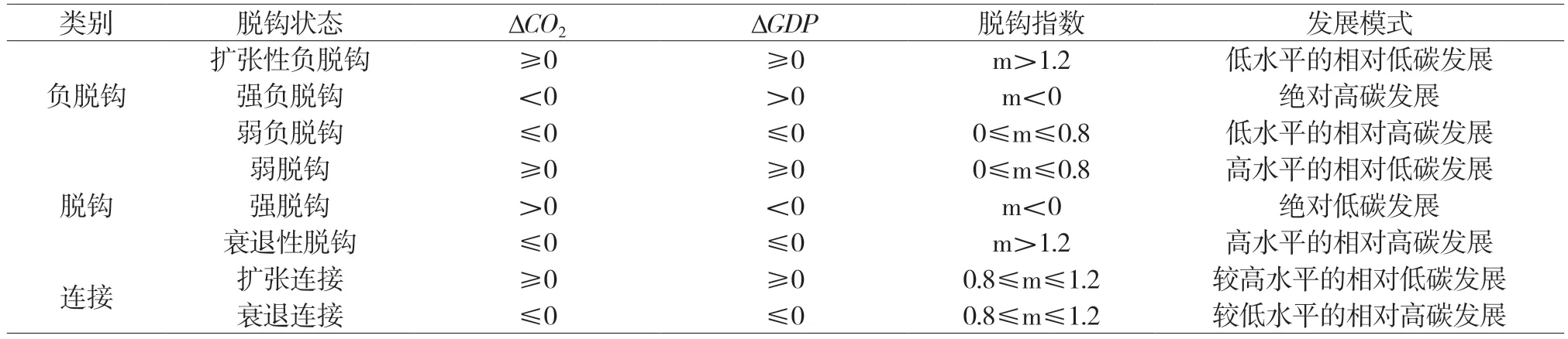
表1 Tapio脱钩程度状态与经济发展相关联脱钩关系

图1 Tapio脱钩程度状态图

在上式中，表示能源消耗相对GDP的弹性，表示二氧化碳相对于能源消耗的弹性，%ΔEC代表能源消耗变化，%ΔCO2代表二氧化碳变化，%GDP代表GDP变化。

3 实证结果分析

3.1 碳排放与经济发展趋势分析

昆钢嘉华公司自2004年成立以来，总资产发展迅速，对区域经济发展产生重要影响。分析其工业占比得知，公司的产业结构并不合理，重工业占比较大，能源消耗过大，经济效益低下。在区域生产总值中，昆钢嘉华公司的贡献率为30%～45%，但能源消耗却超过60%，并且这种现象持续的时间较长。所以，以昆钢嘉华公司为例，研究其碳排放与经济发展的关系，有助于其降低碳排放，有助于提高区域经济收益。近年来昆钢嘉华公司重视绿色环保问题，逐步改革生产技术，提高了能源的利用率，近两年碳排放强度出现降低趋势。

3.2 EKC 实证分析

昆钢嘉华公司经济发展指数用公司的人均产值表示，以公司2010年人均产值数据作为研究基期，从不变价格的计算上进行探讨，进而分析其碳排放、经济发展两者间存在的关联。选择昆钢嘉华公司在2010—2021年度的经营环境和企业成长指数为时间顺序指标，并通过建立模型，再利用Origin Pro 8.5.1对数据进行规整，对其进行一次函数、二次函数和三次函数讨论（见表2）。

通过表2得知，昆钢嘉华公司在一次、二次和三次拟合函数下，数据较为离散。由图2和表3可知，在昆钢嘉华公司中，其3个模型的拟合度 之间的差别比较显著，与一次和二次模型相比，三次模型的更大为 0.939 37，高于0.9。由此，三次模型与昆钢嘉华公司人均产值、人均碳排放的实际情况相符。根据上述内容，得出昆钢嘉华公司人均产值、人均碳排放之间的环境库茨涅茨曲线为“N”型，也就是公司经济的增长有助于提高环境质量，公司人均碳排放的降低会随着公司经济的增长而升高，再次面临环境危机。

表3 昆钢嘉华公司人均产值与人均碳排放线性拟合统计

图2 昆钢嘉华公司人均产值人均碳排放三种情况下的拟合曲线

表2 不同系数设定下经济增长与环境污染的关系

3.3 脱钩分析

在Tapio 脱钩模型的基础上，立足于昆钢嘉华公司经济发展实际和能源消耗实际，建立符合公司碳排放和经济发展之间的脱钩模型。表4则反映了昆钢嘉华公司2010—2021年间碳排放与经济发展的脱钩关系。

表4 昆钢嘉华公司碳排放与经济发展的脱钩关系

可以看出，昆钢嘉华公司在2010—2021年间的碳排放和经济发展之间的脱钩关系波动较大。昆钢嘉华公司成立之后，工业比重逐渐增加，进而导致公司能源消耗总量急剧增加，但消耗更多的能源并未给公司带来良好的经济收益，公司碳排放量增速明显高于生产总值。随着绿色环保概念的宣传推广，公司管理人员逐渐意识到降低碳排放的重要性，并积极采取了有效措施，比如减少高耗能材料的使用，降低高耗能产品占比，与此同时通过现代技术控制和降低碳排放量，逐渐将水电和天然气用于日常生产。基于此，公司的碳排放总量明显降低，出现高新低碳经济发展态势。近期，公司准备进一步转变生产方式，尽可能地落实减排目标，调整产业结构，降低公司碳排放量[5]。公司产业结构的调整是一个长期的动态过程，导致公司的碳排放量和产业之间的发展并不相符，呈现脱钩状态。

4 碳排放影响因素分析

4.1 模型构建及数据说明

Ehrlich &Holdren率先提出IPAT模型（环境压力控制模型），IPAT模型的提出与日益严重的自然环境紧密相关，Ehrlich &Holdren在研究中指出，人口、资产、技术以及政治等方面均对环境质量产生影响。在IPAT 模型中，其中各个影响因素属于关系恒等式，是人口、经济以及技术三者共同产生的影响，单个影响因素对环境不产生影响。具体的关系恒等式如下：

然而在运用 IPAT 模型时，仅能改变其中一个影响因素，而且要保持其他影响因素的稳定。20世纪90年代，Dietz 和 Rosa在IPAT模型的基础上提出了环境影响随机模型，即STIRPAT模型，在STIRPAT模型中，变量可以依据实际情况进行变动。因此，这一模型被学者广泛用于与研究碳排放影响因素中，详细的模型等式如下：

STIRPAT模型中的乘法结构形式与IPAT 模型基本一致，主要在保持三大影响因素不变的情况下引入模型的系数项，一般以a为代表，而b、c、d分别为P、A、T影响因素的指数项，e为模型随机误差项。STIRPAT模型中能高效地分解各个影响因素，同时也能在避免IPAT 模型自变量出现变动的情况下对个系数参数进行评估。然而，在抉择具体数据时，首先要计量这些数据，其次要分析模型具体的对数值，减少模型的异方差，提高因变量与自变量之间弹性值的便利性。

当中，I代表环境压力，如碳排放量等指标，而b、c、d可解释自变量P、A、T变动引起的环境压力变动的弹性系数。在该模型，弹性系数的正负值与相关性呈正相关[6-7]。

本研究选择的为因变量，记为研究对象碳排放量；具体的自变量和解释变量主要有以下几项：（1）F，代表研究对象固定资产投资情况及规模；（2）P，表示人口规模，用公司从业人员数量表示；（3）A，表示企业GDP ；（4）T，表示技术水平，本文中用企业能源利用效率表示。一般来说，技术水平的高低与能源利用效率的高低成正比关系，而与碳排放量则呈相反关系，即技术越高，能源利用效率就越高，碳排放量就越低。

4.2 回归分析

利用最小二乘法分析研究数据，从而得出回归分析结果（见表5）。通过汇总模型了解到，模型的调整R=0.996，F=921.862，且sig=0.000，由此可知数据之间呈显著的相关性，有利于对各变量进行回归分析，计算出的结果更符合设想。然而，表6中的数据表示LnF、LnA、LnT的共线性检验中方差膨胀因子VIF的检验值最小为8.730，最大为148.786。当中LnF、LnA、LnT三变量的值均大于10，由于各变量间存在多重共线性，所以回归得出的结果并不精准。基于此，不应利用无偏估计对LnI、LnF、LnA、LnT数据序列进行研究，为进一步规避的多重共线性对研究带来的消极作用，研究小组将再次改进回归分析法，对具有偏估计的岭回归对模型进行拟合分析[8]。

表5 回归结果

表6 数据回归模型汇总

4.3 碳排放影响因素的岭回归分析

4.3.1 岭回归的定义

通过研究法完成普通最小二乘法估计回归，加入这个变量之间存在多重共线性现象，那么计算出的回归系数方差结果差异较大，估计值也不符合平稳性。根据1970年Hoerl和Kennard的研究结论在改进普通最小二乘法回归的基础上，提出了有偏估计的岭估计法，该方法克服了研究存在的变量问题。

上式为β的岭回归估计，其中k为岭参数，由于已经对数据进行标准化，所以为自变量的样本相关矩阵，且岭回归估计比OLS估计稳定，若k＞0时，该回归为岭回归，若k=0时，该回归为普通最小二乘法估计回归。同时由于k值的变动非唯一性，岭回归估计亦是非唯一的，与k值的变动相符。

4.3.2 岭回归实证分析

本研究通过SPSS22.0工具分析岭回归拟合情况，以此了解影响碳排放的各个因素。不过，由于量的标准系数整体呈平稳状态，加上计算出的各回归系数的岭估计值与设想的基本一致，因此将步长设为0.02，k值范围设为-0.2～0，进而计算执行岭回归（见表7）。

表7 R的平方、岭回归系数估计值及对应值

当时，各变量得出的回归系数比较平稳，目R2=0.986 83，拟合度表现较好。当k=0.06时，LnF、LnP、GDP及LnA、LNT的回归系数的岭回归估计总体处于稳定状态，并与社会经济发展意义相符，之间的残差平方和增长不明显，而且这其间LnF、LnP、LnA、LnT的VIF值均不高于10，与研究条件基本一致。因此，本研究以k=0.06执行标准的岭回归分析（见表8）。

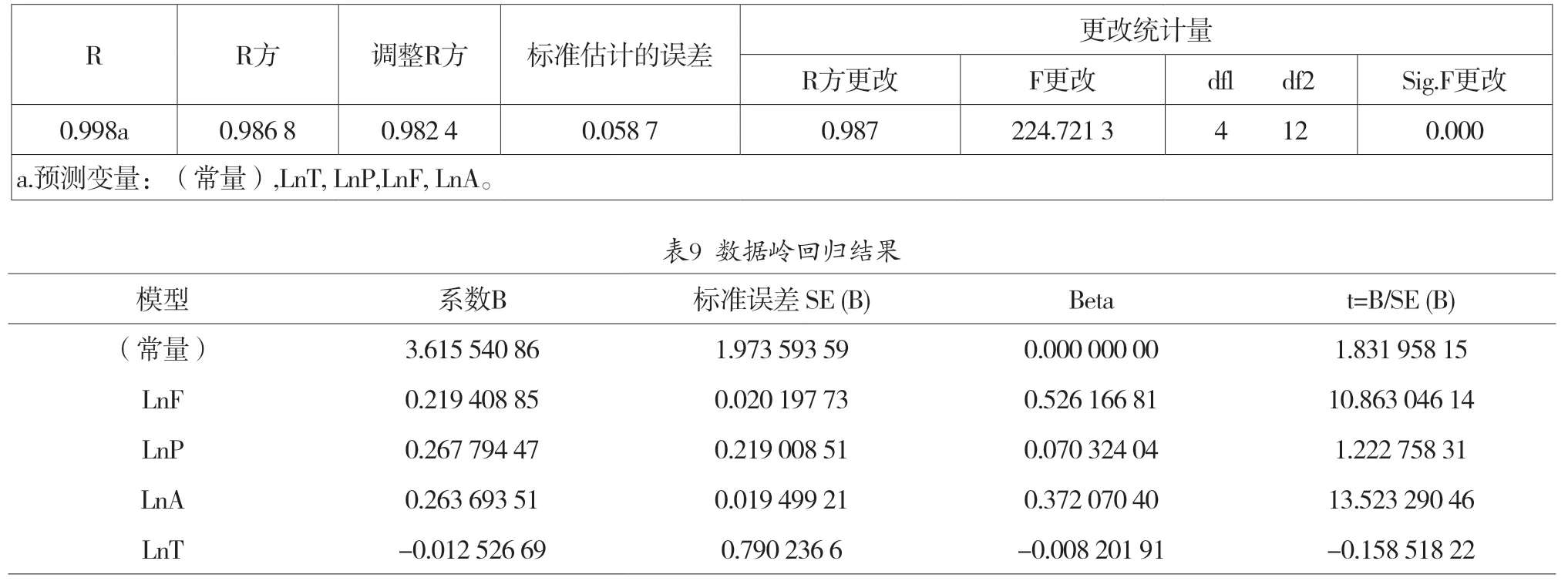
表8 数据回归模型汇总

由表9可知，回归方程的统计量F=224.721 3，且Sig.F=0.000，表示回归方程存在较强的显著性。因此，当自变量出现变化与不同，方程的线性关系更加突出。从而计算标准的岭回归方程，即当k=0.06，R2=0.986 8，LnP、LnA、LnT对应的系数分别为0.466 1、0.357 8、-0.117 8，由此得到研究所用的标准化岭回归方程，具体如下：

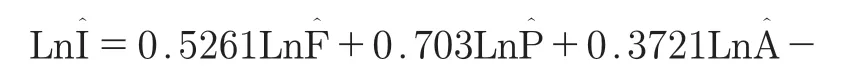
可得企业碳排放影响因素的STIRPAT模型为：

5 结论及启示

5.1 结论

本文以昆钢嘉华公司为研究对象，选取其2010—2021年间的数据分析其碳排放与经济发展之间的关系，通过构建EKC模型和脱钩模型，得出了二者之间的关系；同时在IPAT模型的基础上，分析了影响公司碳排放的因素。

（1）对于昆钢嘉华公司而言，其2010—2021年间碳排放与经济增长之间的关系始终呈增长趋势，但公司碳排放强度与之相反，呈逐渐下降态势。

（2）通过分析昆钢嘉华公司近年来的发展了解到，其碳排放和经济增长之间有着明显的“N”型关系，即使在公司经济总量逐渐增长的背景下，环境质量得到提升，但当经济增长到某个节点时，公司人均碳排放将随着提升，从而出现环境恶化现象。

（3）通过分析昆钢嘉华公司2010—2021年间碳排放、人均产值增加率、脱钩指数之间的关系时，发现曲线发展形势波动较大，总体呈高水平的相对低碳发展趋势。

（4）在分析碳排放影响因素时，通过构建模型发现LnF、LnP、LnA与LnI之间呈正相关关系，但LnT与LnI之间则相反。当中，LnP对LnI的影响程度最高，LnA次之；LnT与LnI之间的关联不明显。

5.2 启示

（1）地方政府应实施具有针对性的低碳奖惩制度，促进地方碳排放交易市场的构建。其一，严格遵守国内碳排放交易试点的原则与发展方向，根据高耗能企业发展实际制定不同的碳排放标准。对积极参与减排的企业给予相应的激励和鼓舞措施，带领其他企业响应减排政策。同时制定严格的处罚条例，不断改进绿色环保、节能减排的法律条例。在构建碳排放交易平台时，要避免程序烦琐，提高企业参与的便利性和积极性，进而提高企业减排的信心[9]。

（2）地方政府应重新审视高碳排放企业在市场中的地位，避免因市场过热导致企业的盲目扩张。通过改变工业经济发展方式，利用内部产业结构调整促使企业达成低碳减排的目标，以促进产业集约化和地方经济的可持续发展。