离散时间正规鞅泛函空间中的广义计数算子
2022-07-28周玉兰孔华芳程秀强
周玉兰, 孔华芳, 程秀强, 薛 蕊, 陈 嘉
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
作为经典 Itô 随机积分理论在算子领域的一种非交换扩张, 量子随机积分理论在不同 Fock 空间框架下有不同的扩张. 其中, 比较著名的 Itô-Clifford 理论[1], 反对称 Fock 空间上的 Fermionic 理论[2],拟自由 Fock 空间上的量子随机变分理论以及自由 Fock 空间上量子关于自由独立 Brown 运动的随机积分理论. 另外, 人们发现, 通过应用连续的 Jordan-Wigner 变换可将Fermionic 情形转换为Bosonic 情形. 以上量子随机分析中所考察的算子都是以指数向量集为其稠密定义域, 算子性质的研究基于指数域而进行. 而由 Attal 等[3]提出的连续时间 Guichardet-Fock 空间, 将量子随机分析理论中算子的定义域扩张到了最大, 脱离了指数域的限制, 同时把上述不同框架下关于连续时间噪声的量子随机积分统一在了 Guichardet-Fock 空间框架下. 众所周知, 物理学中广泛存在着具有增生、湮灭性质的物理系统, 这种作用的具体数学表达式可以用增生、湮灭和计数算子来表示, 称为基本(量子)过程, 在量子随机分析中, 就是以增生、湮灭和保守过程代替了经典分析中的噪声过程, 而适应算子值过程关于基本过程的积分就是量子随机积分. 作为经典鞅(半鞅)表示的推广, 量子鞅(半鞅)的表示已成为量子随机分析中一个很重要的研究内容, 因此, 对增生、湮灭和计数算子(过程)以及相关算子过程性质的讨论对于研究量子随机积分、量子鞅(半鞅)性质显得很重要. 文献[4]讨论了连续时间 Guichardet-Fock 空间L2(Γ;η) 中计数算子的表示问题.
1 预备知识


定理 4[7]计数算子N是L2(M) 中稠定、自伴、闭的、无界线性算子.
2 主要结果




上式右端中令n →+∞, 再结合式(13)可得

必要性. 假定Nh是L2(M) 上的有界线性算子. 反设h不可和, 则由式(14), 有

这与Nh有界矛盾. 从而当Nh有界时,h必可和.
下面讨论广义计数算子序列的收敛性. 对于逐点收敛的函数列, 在一定条件下, 对应的广义计数算子列在其公共稠密定义域上强收敛, 且当极限算子有界时, 广义计数算子列一致收敛.
定理 7 设{hn;n≥0}⊂P+(N) ,{hn;n≥1}逐点收敛于h0且存在常数C>0 , 使得




由控制收敛定理, 有

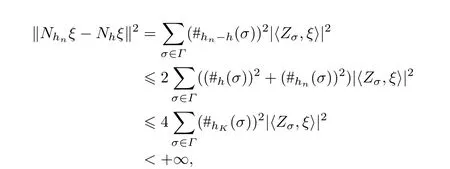
则由控制收敛定理,


从而由Nh,Ng的线性性知NhNg=NgNh在S0(M) 上成立.
若h,g可和, 则Nh,Ng是L2(M) 上有界线性算子, 从而由定理6 可知NhNg=NgNh在全空间上成立.
