关于Bochner 张量具有消灭条件的梯度收缩Kähler-Ricci 孤立子

沈 东, 刘建成

（西北师范大学 数学与统计学院, 兰州 730070）

0 引 言

设 (Mn,gi¯j) 为n维Kähler 流形, 若Mn存在一个实值光滑函数f及λ ∈R 满足方程

Cao[1]提出了Kähler-Ricci 流的概念, 它是几何分析和偏微分方程研究中的一个重要课题, 而梯度Kähler-Ricci 孤立子作为Kähler-Ricci 流的自相似解, 在Kähler-Ricci 流的研究中扮演着重要的角色.所以, 梯度Kähler-Ricci 孤立子的分类对于了解Kähler-Ricci 流的几何结构具有重要意义.

近年来, 关于Kähler 流形中梯度Kähler-Ricci 孤立子的分类问题的研究已取得了一系列重要进展. 例如, 文献[1]在Kähler 流形上引入与黎曼流形中 Weyl 张量相似的概念, 被称为Bochner 张量,并证明了具有消灭Bochner 张量的梯度Kähler-Ricci 孤立子有常全纯截面曲率. 同时证明了具有消灭Bochner 张量的梯度收缩(稳定或扩张) Kähler-Ricci 孤立子是 CPn( Cn或复球面 Bn) 的有限商空间.文献[2]将条件减弱, 即引入了调和Bochner 张量, 且

div(W)=∇lWi¯jk¯l=0.

1 预备知识及引理

同时,

2 Kähler-Ricci 孤立子的积分条件和积分公式

受文献[5]中Ricci 孤立子的积分条件和积分公式的启发, 本章介绍Kähler-Ricci 孤立子的积分条件和积分公式.

性质 1 若 (Mn,gi¯j,f) 是一个具有实值光滑函数f的Kähler-Ricci 孤立子, 则,B,之间满足如下关系式

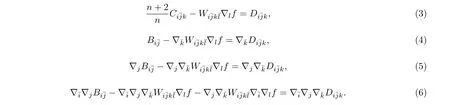
证 明 首先由文献[4]知式 (3) 成立. 再对式 (3) 求散度, 即有

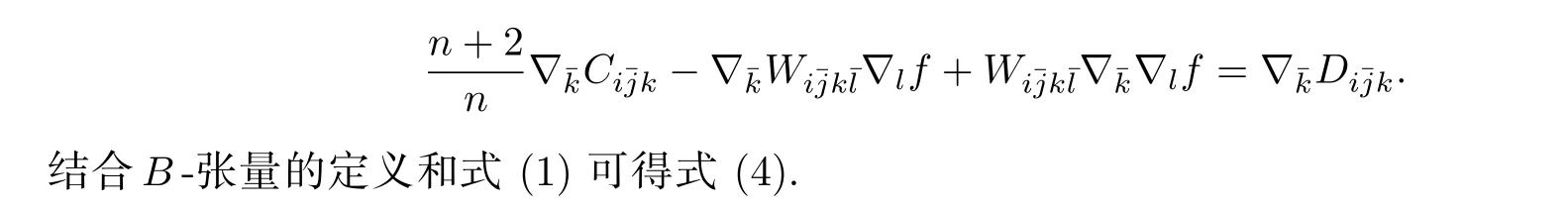
再对式 (4) 求散度, 即得

证 明 由ψ(f) 满足的条件, 利用式 (6) 和式 (1) 可得

对上式整理, 并由式 (2) 得

性质 2 证毕.

3 主要定理的证明

将式 (13) 代入式 (12) 中得

在Mn上Φ(f)≥0 并且在Ωs上Φ(f)=1 , 当s →∞时, 在Mn上则有C ≡0 .

综上所述, 得完备梯度收缩Kähler-Ricci 孤立子具有调和Bochner 张量, 即C ≡0 . 再由引理 2, 则定理 1 得证.