分离双模压缩玻色-爱因斯坦凝聚态并检验其贝尔关联
2022-07-28IVANNIKOVValentinBYRNESTim
孟 鑫, IVANNIKOV Valentin,2, BYRNES Tim,2
(1. 华东师范大学 精密光谱科学与技术国家重点实验室, 上海 200241;2. 上海纽约大学 物理系, 上海 200122)
0 引 言
纠缠作为量子力学的核心内容之一, 是当今现代量子信息技术重要的资源. 产生纠缠需要高度精确的操作和非常低的噪音水平, 一般来说有两种产生纠缠粒子的方法: 第一种方法是通过适当的相互作用精密操控每个粒子, 使它们一个一个地纠缠在一起, 例如, 物理学家们利用这种方法已经成功地产生了多达10 个光子[1]的纠缠态和20 个离子[2]的纠缠态. 第二种方法是通过囚禁粒子, 并对粒子整体进行操控, 使它们共同相互作用演化为一种纠缠态; 这种方法可以使成千上万的原子产生纠缠即玻色-爱因斯坦凝聚态(BEC), 这是物质在极低温度下的一种状态, 内部所有原子都处于同一状态; 虽然这种方法可以用来产生大量纠缠的粒子, 但是缺乏对单个粒子的操控意味着这些系统不适用于完成某些量子信息任务. 本文主要通过对BEC 进行空间分离以改善这种情况.
纠缠最早是由Einstein、Podolsky 、Rosen (EPR) 3 人[3]在1935 年的思想实验上提出的. 1964 年贝尔将EPR 佯谬转换为可被实验验证的贝尔不等式[4], 这激发了大家对非定域性理论的兴趣[5]. 在CHSH 贝尔不等式的指导下[6], Freedman 等[7-10]通过实验证明了纠缠光子对违反贝尔不等式. 尽管该实验存在一些漏洞, 但依然能够从违反贝尔不等式的结论中得出对局域现实论概念性的挑战. 在量子信息中, 量子关联根据相互作用强度可依次分为量子相干、量子关联、EPR 关联、贝尔关联, 其中贝尔关联(即非定域性)代表了量子力学与经典物理学最为深刻的背离.
量子计算、量子模拟和量子精密测量[11]等领域的现代量子技术要求产生和操控由纠缠粒子组成的宏观系统. 因此, 由大量冷原子组成的BEC 就是一种非常合适的研究对象. 本文对双模压缩BEC 进行分离, 得到两个空间分离的BEC 并对其进行观测, 以证明系统内部存在贝尔关联.
1 物理模型
1.1 改变自旋的碰撞
由N个内部状态相同的原子组成的BEC 处于状态

其中,g表示散射过程中的强度. 公式(2)与量子光学中双模压缩态的哈密顿量相同[17-19]. 通过定义
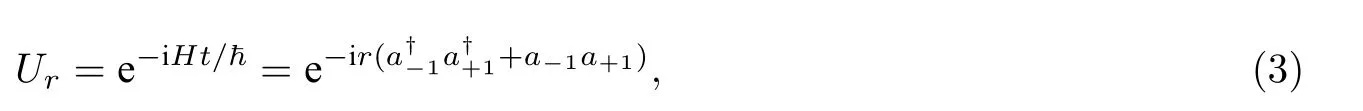
将哈密顿量进行统一变换. 公式(3)中压缩参数(压缩强度)为r=gNt, 其中t表示时间. 在海森堡绘景中压缩算符变为
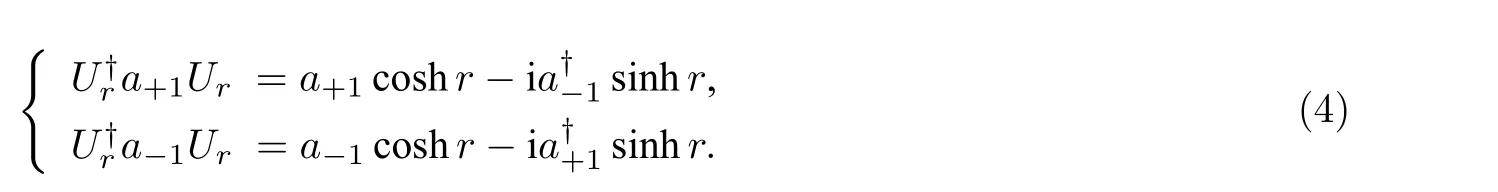
因此, 经过改变自旋的碰撞后, 初始态变为[18,20]

在公式(5)中, 把Fock 态定义为

公式(5)在a−1模和a+1模下有相同数目的Fock 态, 具有双模压缩态的特征. 在本征近似下, 只有+1 模和–1 模被认为是量子态. 由于大量的原子处于0 态, 即便其中有部分原子会转变为+1 态和–1 态, 但相较处于0 态的原子数而言这部分原子的数量并不多. 因此, 可以近似地将0 态当成经典态来处理. 在这个近似下, 根据公式(6), 初始状态(公式(1))对应于真空.
1.2 分离玻色-爱因斯坦凝聚态
2017 年Oudot 等[21]提出了可以通过1 个与状态无关的分束器将BEC 分离. 如图1 所示, 将左边阱的模和湮灭算符am(Alice 的BEC)联系起来, 将右边阱的模和湮灭算符bm(Bob 的BEC)联系起来.空间分离理论上相当于在初态上作用1 个分裂算符, 即[22]

其中,
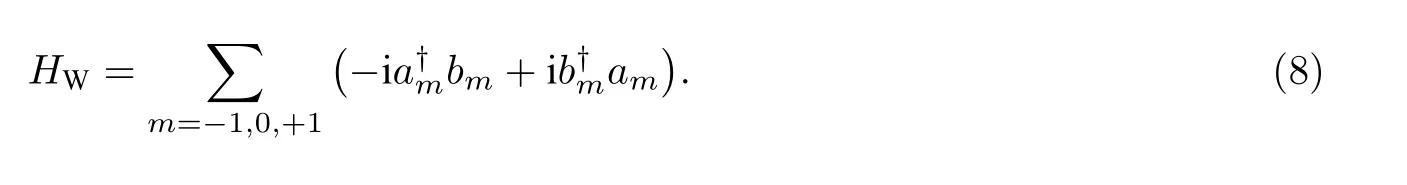
在分裂算符的作用下变为

这种操作类似于光学系统中50/50 分束器的转换. 图1 展示了一种分离方法: 将谐波俘获势能变为双阱势能, 再将2 阱任意分开. 由图1 可知, 通过分束器相互作用, 原子在空间上被分离成2 个系统.分裂后, 2 个BEC 中的原子仍然相互关联, 在2 个阱之间产生贝尔关联.
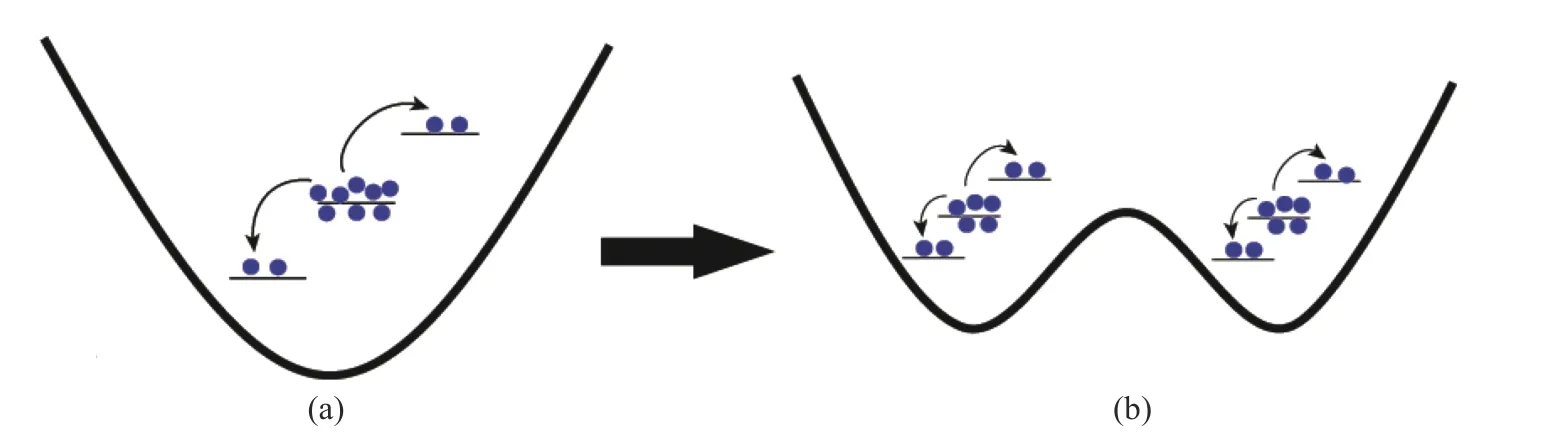
图1 实现分裂双模压缩BEC 的原理图Fig. 1 Schematic for implementing split two-mode compression BECs
将单个BEC 分成2 个阱(a、b)后,N个原子按二项分布的规律随机分布. 为了证明这一点, 本文计算发现, 包含大部分原子的初始状态(公式(1))在分裂后演变为

因此, 每个阱中的原子数满足条件

当N很大时, 最可能出现的结果在Na≈Nb≈N/2 这个范围内.
1.3 局部自旋
接下来将局部自旋算符作用到Alice (A)和Bob (B)的BEC. 局部自旋算符为[23]

布洛赫球沿着y轴的自旋是

通过在+1 态、–1 态的双光子转换实验可以实现局部自旋[14]. 在制备的过程中, 为了计算方便, 还需要在模式m= –1 和m= +1 上加上1 个相对相位. 在相干绘景下, +1 态和–1 态的默认相位演变都是0. 这里引入1 个可控的含时能移 Δ , 因此, 有效哈密顿量变为

实验上, 可以通过在+1 态和–1 态施加1 个磁场或者是交流斯塔克频移(Stark shift)来实现, 即

1.4 测 量
最后, 为了探测到原子的状态, 分别由Alice 和Bob 测量处在am态和bm态的原子个数. 可以通过自旋选择吸收成像法来实现[24], 该方法类似于投影测量, 即

利用此方法测得的原子个数分别记为k和l, 它们将在下面章节中被用来计算贝尔关联.
2 构建贝尔关联态
2.1 分离压缩态
在介绍生成贝尔相关态的方案之前, 首先写出由双模压缩算符Ur和分离算符UW先后作用得到的波函数. 从公式(5)开始, 当r ≪1 时, 有

2.2 态制备方案
这里介绍一种在原子BEC 上产生贝尔相关态的制备方案: 以公式(1)为初态, 将压缩算符U2r作用于态公式(1), 产生 2r=2gNt的压缩; 根据UW(公式 (7) )将BEC 分离为2 个阱.
制备全态的单位算符为

本文发现, 这种方法类似于一种量子光学过程: 在光学系统中, 向分束器发射1 个压缩态, 结果会产生单模压缩和双模压缩的组合[25].
Alice 的粒子数(NA)和Bob 的粒子数(NB)定义为

Alice 的粒子数(NA)和Bob 的粒子数(NB)在子空间中的概率分布为

公式(22)表示的是在Alice 取 (0, NA) 和Bob 取 (0, NB) 这个范围内的联合概率分布.
3 用归一平均值计算贝尔不等式
本文利用Ralph 等人的方法来计算处于分裂压缩态(公式 (19))的贝尔不等式[26]. 希望求值的量是

这里定义

利用旋转算符(公式(15)), 公式(27)变为
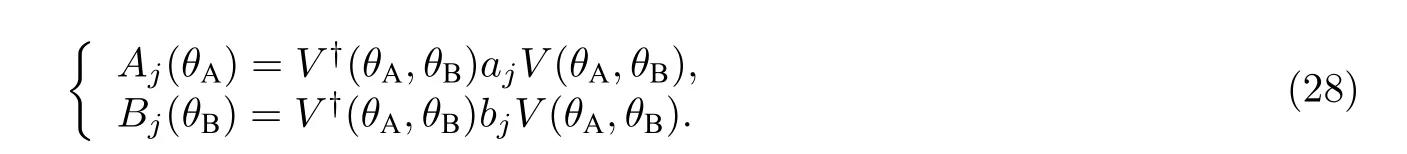
公式(28)中j=±. 公式(25)出现的相关因子可以写为

结合变换公式(4)、公式(9)和公式(27), 可以得到

其中, 最大的违反是在r →0 的情况下,B=. 结果如图2 所示.

图2 Bell-CHSH 不等式中的量(B)随r 的变化Fig. 2 Variation of the quantity in the Bell-CHSH inequality (B) with r
本文发现, 当r≲0.49 , 可以观察到违反贝尔不等式的情况. 正如文献[26]所表达的, 贝尔不等式违反的程度(B)随着压缩强度(r)的增大而减弱. 之所以会出现这种情况, 是因为检测贝尔相关性的算符是用最低阶项(公式(20))构造的. 较大的压缩值会产生额外的高阶项, 从而开始偏离最优相关因子[27-28]. 然而对于较小的r, 造成违反贝尔不等式的主要项是一阶项, 因此作为一阶近似应该接近最佳情况.
4 噪声的影响
本章计算了所考虑的方法对噪声的鲁棒性, 展示了损耗和不完全原子数的分辨率对违反贝尔不等式的影响.
4.1 损 耗
原子系统退相干的主要原因是粒子损失, 即原子从阱中逃逸. 这里采用了一种相对简单的方法来计算损耗. 假设初始态已经准备好, 在没有发生退相干的情况下将旋转算符(公式(15))作用到初始态上, 得到态

发生损耗之后的态为
对于存在损耗的单模n原子系统而言, 克劳斯算符为

可以得出, 公式(37)中所有的γ因子都消失了, 得到了与公式(33)相同的结果. 因此, 对于本文方法,贝尔关联测量值在存在损耗的情况下是不变的.
4.2 探测器分辨率缺陷

在探测无效的情况下, 相关因子变为

由于公式(43)的线性性质, 在存在损耗的情况下, 公式(44)中的相关因子η消失了, 得到了和公式(33)一样的表达式. 因此, 当存在不完全粒子数的测量缺陷时, 通过本文方法计算得到的贝尔关联测量值不变.
5 总结和结论
本文提出了一种检验2 个空间分离BEC 贝尔关联的方法. 制备状态分为两步: 第一步是利用改变自旋的碰撞来产生双模压缩态; 第二步是通过势阱来分离BEC. 这里为了计算贝尔关联, 采用了Ralph 等[26]的方法, 相关因子由粒子数算符的期望值之比来计算. 发现, 当r≲0.49 , 可以观察到贝尔不等式的违反. 在噪声的影响下, 本文所采用的方法对损耗和探测器分辨率问题具有高度鲁棒性.
