从几道考研题谈线性变换与矩阵命题的转化

尹小艳, 施德才

(西安电子科技大学 数学与统计学院,陕西 西安 710071)

0 引言

线性空间的结构及其上的线性变换理论是高等代数的精髓。但由于其概念的高度抽象性和形式的复杂多样性，线性变换历来是线性代数、高等代数教与学的核心和难点，也是各类考试，尤其是研究生招生这类综合性较强的选拔类考试中的重点和热点问题[1-3]。

高等代数中一个重要的数学思想就是化抽象为具体,将抽象的线性变换转化为具体的矩阵问题研究便是这种思想的典型体现。设V为数域P上任意n维线性空间，记L(V)为V上所有线性变换构成的线性空间，记Pn和Pn×n分别为数域P上所有n维向量和所有n阶方阵构成的线性空间。取定V的一组基ε1,ε2,…,εn，则∀α∈V，α在这组基下有唯一的坐标x=(x1,x2,…,xn)T∈Pn与之对应；同时，对任意σ∈L(V),σ在这组基下有唯一的矩阵A与之对应(σ(ε1,ε2,…,εn)=(ε1,ε2,…,εn)A)。于是, 分别在抽象的线性空间V和L(V)与具体简单的空间Pn和Pn×n之间自然地形成两个重要映射:

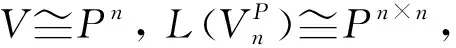
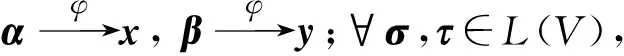
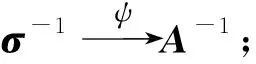
4)σα=λα,α≠0⟺Ax=λx,x≠0，即向量α∈V是线性变换σ的特征向量，当且仅当其坐标x是矩阵A的特征向量；

5) dimσV=rank(A),dimσ-1(0)=n-rank(A)；

6) 记A=(a1,a2,…,an),σ(εi1),σ(εi2),…,σ(εir)为σV的基当且仅当ai1,ai2,…,air为A的列空间的基。

由此，不管V中的元素是什么，也不管V中加法和数乘如何抽象复杂，V中的线性运算都可以转化为Pn中的简单运算；同样，L(V)中线性变换之间抽象的加法、复合、逆变换可以对应为简单、具体、熟悉的矩阵求和、矩阵乘法及矩阵求逆运算。于是, 简单直观的矩阵与向量运算自然成为处理线性变换问题的利器。许多抽象复杂的线性变换问题，转化为对应的矩阵问题，利用矩阵技巧求解，往往给人柳暗花明的惊喜。

1 几个具体的例子

比如欧氏空间中正交变换的分解问题。

定义[1]设η为n维欧氏空间V中一单位向量，线性变换σ,则

σα=α-2(η,α)η

称为镜面反射。

引理2[4]已知σ是n维欧氏空间V上的一个线性变换,σ为镜面反射的充要条件是σ在V的任意一组标准正交基下的矩阵都形如I-2ωωT(称之为镜面反射矩阵), 其中ω为Rn中的单位向量。

由(I-2ωωT)(I-2ωωT)=I知，镜面反射矩阵的逆仍是自身。

例1(2012年浙江大学考研高等代数试题) 已知V是n维欧氏空间。

1)设α0,β0是V上任意两个不同的单位向量, 证明存在一个镜面反射σ, 使得σα0=β0；

2)证明V上任一正交变换都可以表示成一系列镜面反射的乘积。

分析这一命题也可见文献[2], 用线性变换的语言证明非常抽象,过程冗长繁琐，且因为在n维空间上，几何直观性不强，很难理解。

根据引理1，任取V的一组标准正交基ε1,ε2,…,εn，V上任意不同的单位向量α0,β0在这组基下对应于Rn中任意单位向量x,y，镜面反射σ对应于镜面反射矩阵H,σα0=β0当且仅当Hx=y。于是例1用矩阵的语言可描述为：

例21)设x,y是任意两个不同的单位实向量, 证明存在一个镜面反射矩阵H,使得Hx=y；

2)证明任一正交矩阵都可以表示成一系列(最多n个)镜面反射矩阵的乘积。

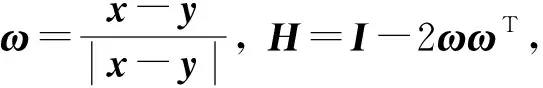
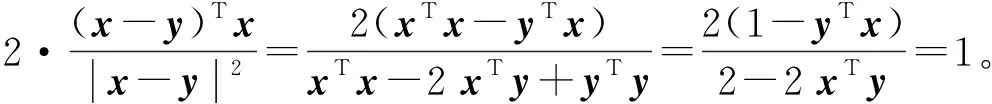
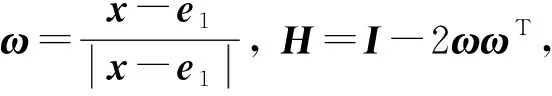
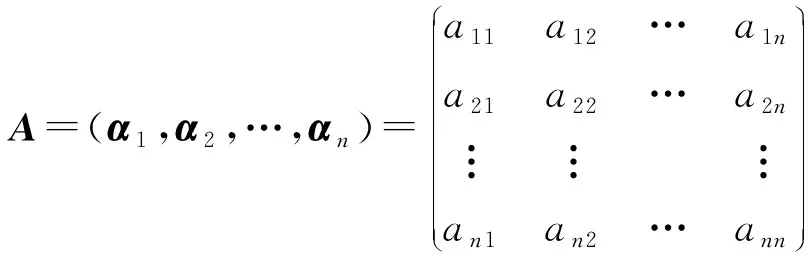
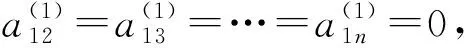
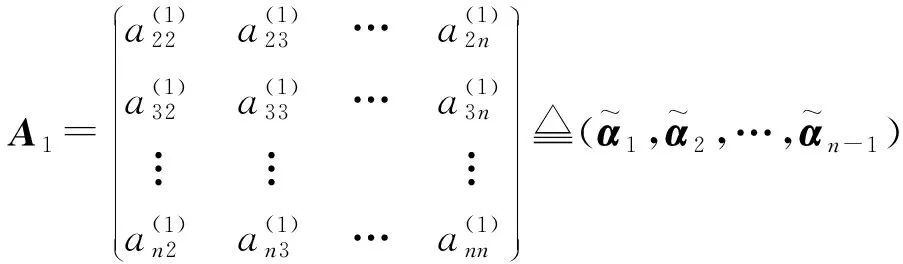
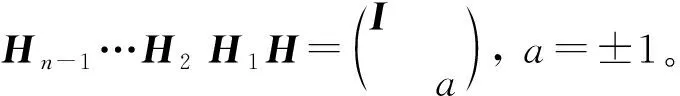
A=(Hn-1…H2H1)-1=H1H2…Hn-1；

若a=-1，有

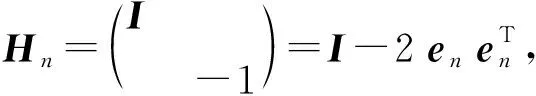
这里用矩阵的语言描述和证明例1,简洁明了、易于接受。为了强调矩阵与线性变换的关系，加强学生对这种转换的理解，用线性变换的语言做进一步说明。

定义σ为σ(ε1,ε2,…,εn)=(ε1,ε2,…,εn)H，由引理2和引理1知，σ为镜面反射变换，且必有σα0=β0。

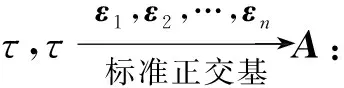
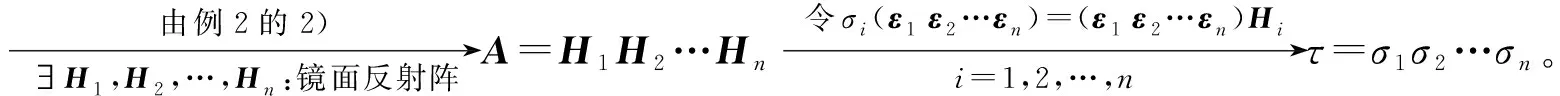
再比如2021年复旦大学硕士研究生入学考试高代试题中有如下线性变换的题目。

例3已知复线性空间V上线性变换φ,ψ满足

φψ-ψφ=φ+ψ,

证明存在V的一组基,使得φ,ψ在这组基下的矩阵都为上三角形。

分析任取空间V的一组基ε1,ε2,…,εn,记线性变换φ,ψ在该基下的矩阵分别为A,B。由引理1，线性变换φ,ψ满足φψ-ψφ=φ+ψ,当且仅当矩阵A,B满足AB-BA=A+B；同时，由相似关系的几何意义(同一线性变换在不同基下的矩阵相似，反之，相似矩阵可以理解为同一线性变换在不同基下的矩阵)知,要证明存在V的一组基,不妨记为e1,e2,…,en，使得φ,ψ在e1,e2,…,en下的矩阵都为上三角形，即要证明矩阵A,B同时相似于三角形矩阵。

于是上述命题等价于如下的矩阵同时相似三角化问题：

例4若复矩阵A,B满足AB-BA=A+B,则A,B可同时相似于上三角形矩阵。

由结论，要证存在可逆矩阵P,使得P-1AP和P-1BP均为上三角形矩阵，将P按列分块，不难发现，满足条件的矩阵P的第1列必为A,B的公共特征向量。一般地，公共特征向量往往是矩阵同时对角化或三角化问题的突破口，找到公共特征向量，再借助于基的扩充定理和数学归纳法便可得到结论。

证明首先证A,B有公共特征向量。

令A+B=C，由AB-BA=A+B知AC-CA=C。取矩阵A的实部最大的特征值λ，对应特征向量α1，即Aα1=λα1。在等式AC-CA=C两端右乘α1，得ACα1=(λ+1)Cα1，于是Cα1=Aα1+Bα1=0，否则λ+1为A的特征值，与λ为A的实部最大的特征值矛盾。从而，Bα1=-Aα1=-λα1，可见α1也是矩阵B的特征向量，对应于特征值-λ。

其次对阶数n做数学归纳以证明原命题。

当n=1时，显然成立。假设命题对n-1阶矩阵成立，以下考虑n阶的情形。

由第一步结论，A,B有公共特征向量α1，且Aα1=λα1,Bα1=-λα1，这里λ为A的实部最大的特征值。将α1扩充成Cn的一组基α1,α2,…,αn，令T=(α1,α2,…,αn)，则T可逆，且

其中A1,B1为n-1阶复矩阵。代入条件AB-BA=A+B可得A1B1-B1A1=A1+B1。

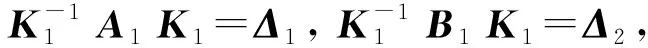
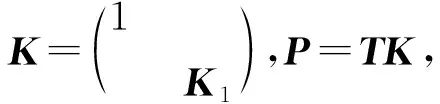
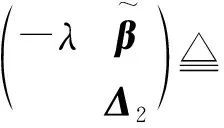
注记1事实上，回到例3线性变换的语言，有

于是，令(e1,e2,…,en)=(ε1,ε2,…,εn)P,则必有φ,ψ在基e1,e2,…,en下的矩阵分别为三角阵Λ和Δ。

当然，也可以利用线性变换的思想方法解决许多棘手的矩阵问题，比如矩阵逆及秩的等式及不等式等[5-6]。下面给出关于矩阵特征向量的命题，若仅从矩阵的角度，较难证明，借助于线性变换的概念，可以容易地解决。

例5[1]设n阶复矩阵A,B满足AB=BA，则A,B有公共特征向量。

用线性变换的语言描述：

例6设V是复数域上的n维线性空间，σ,τ是V上的线性变换，且στ=τσ，证明σ,τ至少有一个公共特征向量。

证明先证若λ是线性变换σ的特征值, 则Vλ={ξ|σξ=λξ}是线性变换τ的不变子空间。事实上, ∀ξ∈Vλ,由σ(τξ)=τσξ=λ(τξ)知τξ∈Vλ。

下证σ,τ至少有一个公共特征向量。

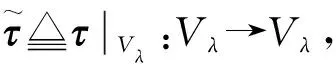
注记2在将矩阵的命题与线性变换的命题相互对应和转换时，要注意基的适当选取。

比如欧氏空间中，正交变换和正交矩阵的对应关系, 对称(反对称)变换与对称(反对称)矩阵的对应关系等，基必须取空间的标准正交基，因为在非标准正交基下,正交变换的矩阵也可能是非正交的, 且正交阵对应的线性变换也可以不是正交变换。

注记3熟练掌握和灵活运用线性变换与矩阵的对应转换，要深刻理解矩阵的几种关系。

1)同一线性变换在不同基下的矩阵相似，反之，相似矩阵必可以看成同一线性变换在不同基下的矩阵，这是矩阵相似关系的几何意义；

2)实对称矩阵合同关系的本质是实二次型在非退化的线性替换前后的矩阵之间的关系，也是同一欧氏空间中不同基的度量矩阵之间的关系。

2 结论

线性空间与线性变换是几何结论，矩阵是代数方法。V与Pn及L(V)与Pn×n的同构映射架起了几何直观和代数方法的桥梁。在高等代数的教学过程中，需要着意强化和反复体现这一重要的数学思想方法，引导学生灵活切换，熟练地用矩阵技巧解决线性变换问题，同时从线性变换观点思考某些矩阵问题。

除同构外，高等代数中还蕴含着许多其他丰富精妙的数学思想，比如等价分类思想、数形结合思想等。在教学过程中，要不断总结、强调和应用这些思想方法，润物无声地提升学生的数学素养和思维品质。