EQ-代数上的(α,β]-模糊前滤子

左卫兵， 刘梦柯

(华北水利水电大学 数学与统计学院,河南 郑州 450046)

0 引言

为了能更好地理解自然语言的语义及发展人类推理的形式理论, NOVK将经典型理论推广,提出了模糊型理论。模糊型理论是一种高阶模糊逻辑,其与经典型理论的最大区别在于真值由二值扩展为多值。随后, NOVK提出了EQ-代数,对EQ-代数进行了详细阐述[1]。众多学者研究了EQ-代数的子类及其相关性质[2-5]。

滤子在研究逻辑代数与相关的逻辑系统完备性中起着非常重要的作用。从逻辑观点来看,滤子与逻辑系统的可证公式密切相关, 滤子也被称为演绎系统。目前,在EQ-代数中各种特殊滤子已经被引入,如固执前滤子、蕴涵前滤子、正蕴涵前滤子等[6-7]。基于模糊集思想, EQ-代数上模糊滤子理论也得到发展,模糊前滤子、模糊蕴涵前滤子、模糊正蕴涵前滤子[8-10]等概念的提出, 丰富了EQ-代数上的滤子理论。

受剩余格上广义模糊滤子相关工作[11-14]的启发,本文在EQ-代数上提出(α,β]-模糊前滤子的概念,进一步定义了(α,β]-模糊正蕴涵前滤子和(α,β]-模糊蕴涵前滤子,得到了这些广义模糊前滤子的等价刻画、性质以及它们之间的关系。

1 预备知识

定义1[1]一个(2,2,2,0)型代数E=〈E,∧,⊗,～,1〉,其中∀x,y,z,s∈E满足

1)〈E,∧,1〉是一个交换幂等幺半群(即有最大元1的∧半格);

2)〈E,⊗,1〉是一个交换幺半群,其中⊗是保序的(x≤y当且仅当x∧y=x);

3)x～x=1；

4)((x∧y)～z)⊗(s～x)≤(z～(s∧y))；

5)(x～y)⊗(z～s)≤(x～z)～(y～s)；

6)(x∧y∧z)～x≤(x∧y)～x；

7)(x∧y)～x≤(x∧y∧z)～(x∧z)；

8)x⊗y≤x～y，

则E是一个EQ-代数。

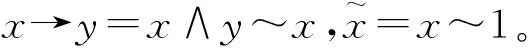
定理1[6]E是一个EQ-代数,∀x,y,z∈E,有下列性质成立：

1)x≤1～x=1→x≤y→x;

2)x→y≤(y→z)→(x→z);

3)x→y≤(z→x)→(z→y);

4)x→y≤(x∧z)→(y∧z);

5)如果x≤y,则z→x≤z→y,y→z≤x→z；

6)x⊗y≤x∧y≤x,y。

定义2[6]若E=〈E,∧,⊗,～,1〉是一个EQ-代数,∅≠F⊆E,如果F满足下列条件，对∀x,y,z∈E,有

L1)1∈F;

L2)如果x∈F,x→y∈F,则有y∈F，

则称F是E的前滤子。

如果它同时满足

L3)如果x→y∈F,则(x⊗z)→(y⊗z)∈F，

则称F为滤子。

定义3[6]前滤子F如果满足

L4)对∀x,y,z∈E,有x→(y→z)∈F,x→y∈F,那么x→z∈F，

称F为正蕴涵前滤子。

如果它同时满足L3),那么F叫做正蕴涵滤子。

定义4[6]若E=〈E,∧,⊗,～,1〉是一个EQ-代数,∅≠F⊆E,如果F满足L1)以及对∀x,y,z∈E,有

L5)如果z→((x→y)→x)∈F,z∈F,则有x∈F，

则称F是E的蕴涵前滤子。

如果它同时满足L3),那么F叫做蕴涵滤子。

设E是EQ-代数,μ:E→[0,1]是一个映射,则称μ为E上的一个模糊集。

2 EQ-代数上的(α,β]-模糊前滤子

定义5若E是一个EQ-代数,α,β∈[0,1]且α<β，如果其模糊集μ满足下列条件，对∀x,y∈E,有

F1)μ(1)∨α≥μ(x)∧β;

F2)μ(y)∨α≥μ(x)∧μ(x→y)∧β，

则称μ为EQ-代数的(α,β]-模糊前滤子。

若它同时满足

F3)∀x,y,z∈E,μ(x→y)∨α≥μ((x⊗z)→(y⊗z))∧β，

则称其为(α,β]-模糊滤子。

例1设E=({0,a,b,c,1},∧,⊗,～,1),其中0≤a,b≤c≤1,运算“⊗”,“～”及“→”分别定义为

0abc1～0abc1→0abc100000001ba00011111a0a0aab00bbb,ab11aaba11bb,ab1b11baa111,c0abccc0ab1cc0ab1110abc110abc110abc1

则E是一个EQ-代数[7]。

设模糊集μ有如下形式:μ(0)=r1,μ(a)=r2,μ(b)=r3,μ(c)=r4,μ(1)=r5,其中0

设μ是EQ-代数上的模糊集,t∈(0,1],集合μt={x∈t|μ(x)≥t}称为μ的水平集。

定理2EQ-代数上的模糊集μ是(α,β]-模糊前滤子,当且仅当对于∀t∈(α,β],非空集合μt是E的前滤子。

证明(必要性)若x∈μt,则μ(x)≥t,μ(1)∨α≥μ(x)∧β≥t∧β=t,所以μ(1)≥t,从而1∈μt;设x,x→y∈μt,则μ(x),μ(x→y)≥t,μ(y)∨α≥μ(x)∧μ(x→y)∧β≥t∧β=t,有μ(y)≥t,即y∈μt,所以μt是E的前滤子。

(充分性)∀t0∈(α,β],非空集合μt是E的前滤子。令t0=μ(x)∧β,μt0是E的前滤子,有1∈μt0,则μ(1)∨α≥μ(1)≥t0=μ(x)∧β;令t1=μ(x)∧μ(x→y)∧β,所以μ(x)≥t1,即x∈μt1,μ(x→y)≥t1,即x→y∈μt1,因μt1是E的前滤子,所以y∈μt1,因此有μ(y)∨α≥μ(y)≥t1=μ(x)∧μ(x→y)∧β。所以μ是(α,β]-模糊前滤子。

定理3EQ-代数上的模糊集μ是(α,β]-模糊前滤子, 有下列性质成立:

1)∀x,y∈E,x≤y蕴涵μ(y)∨α≥μ(x)∧β;

2)∀x,y,z∈E,μ(x→z)∨α≥μ(x→y)∧μ(y→z)∧β。

证明1)x≤y有x→y=1,从而μ(x→y)=μ(1)。由F1)可知μ(1)∨α≥μ(x)∧β,即μ(x→y)∨α≥μ(x)∧β。由μ(y)∨α≥μ(x)∧μ(x→y)∧β,得μ(y)∨α≥(μ(x)∧μ(x→y)∧β)∨α=(μ(x)∨α)∧(μ(x→y)∨α)∧(β∨α)≥(μ(x)∨α)∧(μ(x)∧β)∧β=μ(x)∧β,即μ(y)∨α≥μ(x)∧β。

2)x→y≤(y→z)→(x→z),则μ((y→z)→(x→z))∨α≥μ(x→y)∧β。μ是(α,β]-模糊前滤子,所以μ(x→z)∨α≥μ(y→z)∧μ((y→z)→(x→z))∧β≥μ(y→z)∧μ(x→y)∧β∧β=μ(y→z)∧μ(x→y)∧β。

3 EQ-代数上的(α,β]-模糊正蕴涵前滤子

定义6若E是一个EQ-代数, 如果其模糊集μ满足下列条件，对∀x,y,z∈E, 有

FF1)∀x∈E,μ(1)∨α≥μ(x)∧β;

FF2)∀x,y∈E,μ(y)∨α≥μ(x)∧μ(x→y)∧β;

FF3)∀x,y∈E,μ(x→z)∨α≥μ(x→(y→z))∧μ(x→y)∧β,

则称μ为EQ-代数的(α,β]-模糊正蕴涵前滤子。

若同时满足F3),则称其为(α,β]-模糊正蕴涵滤子。

例2设E=({0,a,b,c,1},∧,⊗,～,1),其中0

0abc1～0abc1→0abc100000001ba00011111a0a0aab00bbb,ab11aaba11bb,ab1b11baa111,c0abccc0ab1cc0ab1110abc110abc110abc1

则E是一个EQ-代数[7]。

模糊集μ形式如下:μ(0)=r1,μ(a)=r2,μ(b)=μ(c)=r3,μ(1)=r4，其中0

定理4EQ-代数上的模糊集μ是(α,β]-模糊正蕴涵前滤子，当且仅当对于∀t∈(α,β],非空集合μt是E的正蕴涵前滤子。

证明(必要性) 由定理2知只需证L3)。若x→(y→z),x→y∈μt,则μ(x→(y→z)),μ(x→y)≥t,从而μ(x→z)∨α≥μ(x→(y→z))∧μ(x→y)∧β≥t∧β=t,即μ(x→z)≥t,所以x→z∈μt,故μt是E的正蕴涵前滤子。

(充分性) 由定理2知只需证FF3)。∀t∈(α,β],则对于∀x,y,z∈E

1)若μ(x→(y→z))∧μ(x→y)≤α，有μ(x→z)∨α≥α≥μ(x→(y→z))∧μ(x→y)≥μ(x→(y→z))∧μ(x→y)∧β,即FF3)成立;

2)若μ(x→(y→z))∧μ(x→y)>α，令t=μ(x→(y→z))∧μ(x→y)∧β,则μ(x→(y→z))≥μ(x→(y→z))∧μ(x→y)∧β=t,μ(x→y)≥μ(x→(y→z))∧μ(x→y)∧β=t,所以x→(y→z)∈μt,x→y∈μt,又因μt是E的正蕴涵前滤子得x→z∈μt,所以μ(x→z)∨α≥μ(x→z)≥t=μ(x→(y→z))∧μ(x→y)∧β, 所以μ是(α,β]-模糊正蕴涵前滤子。

定理5设μ和ν是E上的两个(α,β]-模糊前滤子,μ⊆ν且(μ(1)∨α)∧β=(ν(1)∨α)∧β,如果μ是E上的(α,β]-模糊正蕴涵前滤子, 则ν也是E上的(α,β]-模糊正蕴涵前滤子。

证明由μ⊆ν得

ν(x∧(x→y)→y)∨α≥μ(x∧(x→y)→y)∨α≥μ(x∧(x→y)→(x→y))∧μ(x∧(x→y)→x)∧β,

由x∧(x→y)≤x,x∧(x→y)≤x→y,得x∧(x→y)→x=1,x∧(x→y)→(x→y)=1，所以

μ(x∧(x→y)→x)=μ(1),μ(x∧(x→y)→(x→y))=μ(1),

因此

ν(x∧(x→y)→y)∨α≥μ(x∧(x→y)→y)∨α≥μ(1)∧β,

从而

ν(x∧(x→y)→y)∨α=(μ(1)∧β)∨α=(μ(1)∨α)∧(β∨α)=(μ(1)∨α)∧β=(ν(1)∨α)∧β。

另有x→(y→z)≤x∧y→y∧(y→z),x→y≤x→x∧y,所以

ν(x∧y→y∧(y→z))∨α≥ν(x→(y→z))∧β,ν(x→x∧y)∨α≥ν(x→y)∧β,

因而可得

(ν(x∧y→y∧(y→z))∧ν(x→x∧y))∨α≥ν(x→(y→z))∧ν(x→y)∧β,

从而

((ν(x∧y→y∧(y→z))∧ν(x→x∧y))∨α)∧β=

((ν(x∧y→y∧(y→z))∧ν(x→x∧y))∧β)∨(α∧β)≥ν(x→(y→z))∧ν(x→y)∧β,

由定理3的2)可得

ν(x→y∧(y→z))∨α≥ν(x∧y→y∧(y→z))∧ν(x→x∧y)∧β,

从而

ν(x→y∧(y→z))∨α≥(ν(x∧y→y∧(y→z))∧ν(x→x∧y)∧β)∨α≥

ν(x→(y→z))∧ν(x→y)∧β;ν(x→z)∨α≥ν(x→y∧(y→z))∧ν(y∧(y→z)→z)∧β,

从而

ν(x→z)∨α≥(ν(x→y∧(y→z))∧ν(y∧(y→z)→z)∧β)∨α=

(ν(x→y∧(y→z))∨α)∧(ν(y∧(y→z)→z)∨α)∧(β∨α),

再由ν(x∧(x→y)→y)∨α=(ν(1)∨α)∧β，得ν(y∧(y→z)→z)∨α=(ν(1)∨α)∧β,所以

ν(x→z)∨α≥(ν(x→y∧(y→z))∨α)∧((ν(1)∨α)∧β)∧β≥ν(x→y∧(y→z))∧(ν(1)∨α)∧β,

再由x→y≤1,得ν(1)∨α≥ν(x→y)∧β,因此

ν(x→z)∨α≥ν(x→(y→z))∧ν(x→y)∧β。

即FF3)成立，故ν是(α,β]-模糊正蕴涵前滤子。

定理6设μ是E上的(α,β]-模糊前滤子, 则μ是(α,β]-模糊正蕴涵前滤子，当且仅当∀x,y∈E,μ(x→y)∨α≥μ(x→(x→y))∧β。

证明已知x→(x→y)≤1,由定理3的1)可得μ(1)∨α≥μ(x→(x→y))∧β,μ是(α,β]-模糊正蕴涵前滤子, 则

μ(x→y)∨α≥μ(x→(x→y))∧μ(x→x)∧β=μ(x→(x→y))∧μ(1)∧β,

所以

μ(x→y)∨α≥(μ(x→(x→y))∧μ(1)∧β)∨α=

(μ(x→(x→y))∨α)∧(μ(1)∨α)∧β≥μ(x→(x→y))∧β。

反之需证FF3)。已知

x→(y→z)≤((y→z)→(x→z))→(x→(x→z)),x→y≤(y→z)→(x→z),

则由定理3的1)得

μ((y→z)→(x→z))∨α≥μ(x→y)∧β,μ(((y→z)→(x→z))→(x→(x→z)))∨α≥μ(x→(y→z))∧β,

所以

(μ((y→z)→(x→z))∧μ(((y→z)→(x→z))→(x→(x→z))))∨α≥μ(x→y)∧μ(x→(y→z))∧β,

从而

((μ((y→z)→(x→z))∧μ(((y→z)→(x→z))→(x→(x→z))))∨α)∧β=

((μ((y→z)→(x→z))∧μ(((y→z)→(x→z))→(x→(x→z))))∧β)∨(α∧β)≥

μ(x→y)∧μ(x→(y→z))∧β。

另由μ是(α,β]-模糊前滤子,得

(μ(x→(x→z))∨α)∨α=μ(x→(x→z))∨α≥μ(x→y)∧μ(x→(y→z))∧β,

所以

(μ(x→(x→z))∨α)∧β=(μ(x→(x→z))∧β)∨(α∧β)≥μ(x→y)∧μ(x→(y→z))∧β,

因此

μ(x→z)∨α≥(μ(x→(x→z))∧β)∨α≥μ(x→y)∧μ(x→(y→z))∧β,

所以μ是(α,β]-模糊正蕴涵前滤子。

定义7若μ是E中的(α,β]-模糊前滤子, 若它满足对于∀x,y,z∈E,μ(x→(y→z))=μ(y→(x→z)),则称μ具有弱交换性。

定理7设μ是E上满足弱交换性的(α,β]-模糊前滤子, 则μ是(α,β]-模糊正蕴涵前滤子,当且仅当∀x,y,z∈E,μ((x→y)→(x→z))∨α≥μ(x→(y→z))∧β。

证明已知μ满足弱交换性且是(α,β]-模糊正蕴涵前滤子, 则

μ((x→y)→(x→y))=μ(x→((x→y)→y))=μ(1);(x→y)→y≤(y→z)→((x→y)→z),

故

x→((x→y)→y)≤x→((y→z)→((x→y)→z)),

所以

μ(x→((y→z)→((x→y)→z)))∨α≥μ(x→((x→y)→y))∧β=μ(1)∧β。

另外

μ(x→((x→y)→z))∨α≥μ(x→((y→z)→((x→y)→z)))∧μ(x→(y→z))∧β,

所以

μ((x→y)→(x→z))∨α=μ(x→((x→y)→z))∨α≥

μ(x→((y→z)→((x→y)→z)))∧μ(x→(y→z))∧β,

从而

μ((x→y)→(x→z))∨α≥(μ(x→((y→z)→((x→y)→z)))∧μ(x→(y→z))∧β)∨α=

(μ(x→((y→z)→((x→y)→z)))∨α)∧(μ(x→(y→z))∨α)∧(α∨β)≥

(μ(1)∧β)∧(μ(x→(y→z))∨α)∧β≥μ(1)∧β∧μ(x→(y→z))=μ(x→(y→z))∧β。

反之只需证FF3)。已知μ是(α,β]-模糊前滤子,则μ(x→z)∨α≥μ(x→y)∧μ((x→y)→(x→z))∧β,故

μ(x→z)∨α≥(μ(x→y)∧μ((x→y)→(x→z))∧β)∨α=

(μ(x→y)∨α)∧(μ((x→y)→(x→z))∨α)∧β≥μ(x→y)∧μ(x→(y→z))∧β,

所以μ是(α,β]-模糊正蕴涵前滤子。

4 EQ-代数上的(α,β]-模糊蕴涵前滤子

定义8若E是一个EQ-代数, 如果其模糊集μ满足下列条件，对∀x,y,z∈E, 有

IF1)∀x∈E,μ(1)∨α≥μ(x)∧β;

IF2)∀x,y,z∈E,μ(x)∨α≥μ(z→((x→y)→x))∧μ(z)∧β,

则称μ为EQ-代数的(α,β]-模糊蕴涵前滤子。

若同时满足F3),则称其为(α,β]-模糊蕴涵滤子。

例3设E=({0,a,b,c,1},∧,⊗,～,1),其中0

0abc1～0abc1→0abc100000001ba00011111a0a0aab00bbb,ab11aaba11bb,ab1b11baa111,c0abccc0ab1cc0ab1110abc110abc110abc1

则E是一个EQ-代数[7]。

模糊集μ形式如下：μ(0)=r1,μ(a)=r2,μ(b)=r3,μ(c)=r4,μ(1)=r5,其中0

则可验证μ为EQ-代数上的(α,β]-模糊蕴涵前滤子。

定理8EQ-代数上的模糊集μ是(α,β]-模糊蕴涵前滤子，当且仅当对于∀t∈(α,β],非空集合μt是E的蕴涵前滤子。

证明(必要性) 若x∈μt,则μ(x)≥t,μ(1)∨α≥μ(x)∧β≥t∧β=t,所以μ(1)≥t,从而1∈μt;若z→((x→y)→x),z∈μt,则μ(z→((x→y)→x)),μ(z)≥t,从而μ(x)∨α≥μ(z→((x→y)→x))∧μ(z)∧β≥t∧β=t,即μ(x)≥t,故x∈μt,所以μt是E的蕴涵前滤子。

(充分性) ∀t1∈(α,β],∀x∈E,令t1=μ(x)∧β,μt是E的蕴涵前滤子,所以1∈μt1,则μ(1)≥t1,从而μ(1)∨α≥μ(1)≥t1=μ(x)∧β;∀t2∈(α,β],∀x,y,z∈E,令t2=μ(z→((x→y)→x))∧μ(z)∧β,则μ(z→((x→y)→x))≥t2,μ(z)≥t2,因此z→((x→y)→x)∈μt2,z∈μt2,故x∈μt2。所以

μ(x)∨α≥μ(x)≥t2=μ(z→((x→y)→x))∧μ(z)∧β,

所以μ是(α,β]-模糊蕴涵前滤子。

定理9EQ-代数上的模糊集μ是(α,β]-模糊前滤子,若对于∀x,y∈E,x≤y,则μ(y)∨α≥μ(x)∧β。

证明已知x≤y,则有x→y=1,y≤1→y=(y→y)→y,由定理1的5)可知x→(y→y)→y≥x→y=1,所以x→(y→y)→y=1,故

μ(y)∨α≥μ(x→((y→y)→y))∧μ(x)∧β=μ(1)∧μ(x)∧β,

由此可得

μ(y)∨α≥(μ(1)∧μ(x)∧β)∨α=(μ(1)∨α)∧(μ(x)∨α)∧β≥

(μ(x)∧β)∧(μ(x)∨α)∧β=μ(x)∧β。

定理10设μ是E上的(α,β]-模糊前滤子, 则μ是(α,β]-模糊蕴涵前滤子，当且仅当∀x,y∈E,μ(x)∨α≥μ((x→y)→x)∧β。

证明已知μ(x)∨α≥μ(z→((x→y)→x))∧μ(z)∧β。令z=1,得

μ(x)∨α≥μ(1→((x→y)→x))∧μ(1)∧β,(x→y)→x≤1→((x→y)→x),

则μ(1→((x→y)→x))∨α≥μ((x→y)→x)∧β,因此

μ(x)∨α≥(μ(1→((x→y)→x))∧μ(1)∧β)∨α=(μ(1→((x→y)→x))∨α)∧(μ(1)∨α)∧β≥

μ((x→y)→x)∧β∧(μ(1)∨α)∧β=μ((x→y)→x)∧β∧(μ(1)∨α)。

又因为(x→y)→x≤1,所以μ(1)∨α≥μ((x→y)→x)∧β,从而可得μ(x)∨α≥μ((x→y)→x)∧β。

反之需证IF2)。已知μ是(α,β]-模糊前滤子,所以μ((x→y)→x)∨α≥μ(z→((x→y)→x))∧μ(z)∧β,由μ(x)∨α≥μ((x→y)→x)∧β,得

μ(x)∨α≥(μ((x→y)→x)∧β)∨α=(μ((x→y)→x)∨α)∧(α∨β),

故

μ(x)∨α≥(μ((x→y)→x)∨α)∧β≥μ(z→((x→y)→x))∧μ(z)∧β,

因此μ是(α,β]-模糊蕴涵前滤子。

定理11设μ和ν是E上的两个(α,β]-模糊前滤子,μ⊆ν且(μ(1)∨α)∧β=(ν(1)∨α)∧β,如果μ是E上满足弱交换性的(α,β]-模糊蕴涵前滤子, 则ν也是E上的(α,β]-模糊蕴涵前滤子。

证明设z=(x→y)→x,已知z≤1,x≤1→x,由定理15)可得x≤1→x≤z→x,所以(z→x)→y≤x→y,z=(x→y)→x≤((z→x)→y)→x,故z→(((z→x)→y)→x)=1,则μ(z→(((z→x)→y)→x))=μ(1),由弱交换性得μ(((z→x)→y)→(z→x))=μ(1)。因为μ是(α,β]-模糊蕴涵前滤子, 则由定理10得

μ(1)∧β=μ(((z→x)→y)→(z→x))∧β≤μ(z→x)∨α,

故(μ(1)∧β)∨α≤μ(z→x)∨α,从而

(ν(1)∨α)∧β=(μ(1)∨α)∧β=(μ(1)∧β)∨(α∧β)≤μ(z→x)∨α≤ν(z→x)∨α。

又因ν是(α,β]-模糊前滤子, 所以有ν(x)∨α≥ν(z→x)∧ν(z)∧β,故

ν(x)∨α≥(ν(z→x)∧ν(z)∧β)∨α=(ν(z→x)∨α)∧(ν(z)∨α)∧(β∨α)≥

((ν(1)∨α)∧β)∧(ν(z)∨α)∧β≥(ν(z)∧β)∧(ν(z)∨α)∧β≥

(ν(z)∧β)∧ν(z)∧β=ν(z)∧β,

即ν(x)∨α≥ν(z)∧β=ν((x→y)→x)∧β。最后由定理10可得,ν是(α,β]-模糊蕴涵前滤子。

定理12每个(α,β]-模糊蕴涵前滤子是(α,β]-模糊前滤子。

证明已知y≤1→y,所以x→y≤x→(1→y)由定理9得

μ(x→((y→1)→y))∨α=μ(x→(1→y))∨α≥μ(x→y)∧β,

由(α,β]-模糊蕴涵前滤子的定义得,μ(y)∨α≥μ(x→((y→1)→y))∧μ(x)∧β,则

μ(y)∨α≥(μ(x→((y→1)→y))∧μ(x)∧β)∨α=

(μ(x→((y→1)→y))∨α)∧(μ(x)∨α)∧(β∨α)≥μ(x→y)∧β∧(μ(x)∨α)∧β≥μ(x→y)∧μ(x)∧β,

即F2)。

定理13每个(α,β]-模糊蕴涵前滤子是(α,β]-模糊正蕴涵前滤子。

证明由定理12知只需证FF3)。已知x∧(x→y)≤x,由定理15)得,x→y≤x∧(x→y)→y,再由x∧(x→y)≤x→y,得x∧(x→y)≤x∧(x→y)→y,故(x∧(x→y)→y)→y≤(x∧(x→y))→y,因此((x∧(x→y)→y)→y)→((x∧(x→y))→y)=1。由定理10可得

μ(x∧(x→y)→y)∨α≥μ(((x∧(x→y)→y)→y)→(x∧(x→y)→y))∧β=μ(1)∧β，

x→(y→z)≤x∧y→(y∧(y→z)),x→y≤x→(x∧y)。

故

μ(x∧y→(y∧(y→z)))∨α≥μ(x→(y→z))∧β,μ(x→(x∧y))∨α≥μ(x→y)∧β,

因此可得

(μ(x∧y→(y∧(y→z)))∧μ(x→(x∧y)))∨α≥μ(x→(y→z))∧μ(x→y)∧β,

则

((μ(x∧y→(y∧(y→z)))∧μ(x→(x∧y)))∨α)∧β≥μ(x→(y→z))∧μ(x→y)∧β,

所以

((μ(x∧y→(y∧(y→z)))∧μ(x→(x∧y)))∨α)∧β=

((μ(x∧y→(y∧(y→z)))∧μ(x→(x∧y)))∧β)∨(α∧β)=

((μ(x∧y→(y∧(y→z)))∧μ(x→(x∧y)))∧β)∨α。

再由定理3的2)知

μ(x→(y∧(y→z)))∨α≥μ(x∧y→(y∧(y→z)))∧μ(x→(x∧y))∧β，

故

μ(x→(y∧(y→z)))∨α≥(μ(x∧y→(y∧(y→z)))∧μ(x→(x∧y))∧β)∨α≥

μ(x→(y→z))∧μ(x→y)∧β,

又可知μ(y∧(y→z)→z)∨α≥μ(1)∧β,所以

(μ(x→(y∧(y→z)))∧μ(y∧(y→z)→z))∨α≥μ(x→(y→z))∧μ(x→y)∧μ(1)∧β,

从而

((μ(x→(y∧(y→z)))∧μ(y∧(y→z)→z))∨α)∧β≥μ(x→(y→z))∧μ(x→y)∧μ(1)∧β,

((μ(x→(y∧(y→z)))∧μ(y∧(y→z)→z))∨α)∧β=(μ(x→(y∧(y→z))∧μ(y∧(y→z)→z)β∨(α∧β)。

由定理3的2)知

μ(x→z)∨α≥μ(x→(y∧(y→z)))∧μ(y∧(y→z)→z)∧β,

所以

μ(x→z)∨α≥(μ(x→(y∧(y→z)))∧μ(y∧(y→z)→z)∧β)∨α≥μ(x→(y→z))∧μ(x→y)∧μ(1)∧β,

进而有

μ(x→z)∨α≥(μ(x→(y→z))∧μ(x→y)∧μ(1)∧β)∨α=

(μ(x→(y→z)∨α))∧(μ(x→y)∨α)∧(μ(1)∨α)∧β≥μ(x→(y→z))∧μ(x→y)∧(μ(x→y)∧β)∧β,

即

μ(x→z)∨α≥μ(x→(y→z))∧μ(x→y)∧β,

因此μ是(α,β]-模糊正蕴涵前滤子。

5 总结

本文在EQ-代数的基础上, 提出了(α,β]-模糊前滤子, (α,β]-模糊正蕴涵前滤子以及(α,β]-模糊蕴涵前滤子的概念, 研究了这三类模糊前滤子的性质, 得到了它们的等价刻画, 讨论了三者之间的关系, 得到了每个(α,β]-模糊蕴涵前滤子是(α,β]-模糊前滤子, 以及每个(α,β]-模糊蕴涵前滤子是(α,β]-模糊正蕴涵前滤子的结论, 对于在EQ-代数上的其他滤子研究具有积极的参考价值。