论相对论性量子矩阵力学(S=ћ/2)

李宜和

(河南财政金融学院 人工智能学院，河南 郑州 450046)

0 序言

1925年,海森堡提出了矩阵力学[1]；1926年，薛定谔提出了波动力学[2]，同时他证明了这两种力学是等价的。然而，波动力学更容易被人们所接受，并且应用它能很好地解决实际问题，因此人们对矩阵力学的关注越来越少。当狄拉克提出相对论性波动力学后，没有人再研究相对论性矩阵力学的表达式，人们想当然地认为海森堡的矩阵力学也适用于相对论性微观领域。一方面，显然没有足够的证据证明这个推论是正确的，然而，如果把海森堡方程应用到相对论性微观领域，将会得到一些相互矛盾的结果；另一方面，还有一些物理问题需要解决，如四维速度的算符形式如何表达等。下面将详细讨论这些问题。

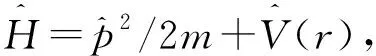
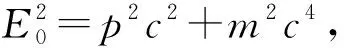
在相对论力学中，定义了四维速度的概念以及它与四维动量的关系，同样确定了四维速度的空间分量与三维速度的关系。但是，到目前为止，在相对论性量子力学中却找不到它们相应的算符形式以及它们之间的算符关系。因此,必须找到一个新的相对论性矩阵方程代替海森堡方程，从而能很好地解决上述问题。本文在第1节给出新的相对论性矩阵方程，其在非相对论情况下就是海森堡方程；在第2节用这个新的矩阵力学方程解决上述问题，详细讨论海森堡方程不适用于相对论性量子力学而人们却普遍认为海森堡方程适用于相对论性量子力学的原因；最后部分是总结及展望。

1 相对论性矩阵力学

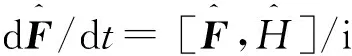
根据狭义相对论

(1)

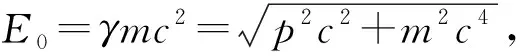
(2)

(3)

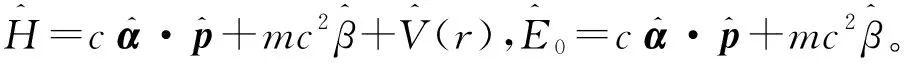
方程(3)是否为新的相对论性矩阵方程，取决于两个方面。一方面它要满足在非相对论条件下转变为海森堡方程，另一方面它要能解决引言中海森堡方程所遇到的困难。首先考虑非相对论极限，由狄拉克方程[7]

(4)

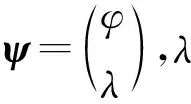
(5)

令E′=E-mc2，忽略低级项，则方程(5)变为

(6)

此即为非相对论下的薛定谔方程。

可以看出，在非相对论极限下，

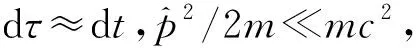
2 新的相对论性矩阵方程的应用

2.1 四维速度与四维动量

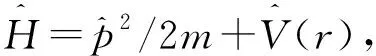
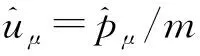
(7)

(8)

(9)

(10)

由此可知，无论是自由粒子或带电粒子在电磁场中，这些公式都与物理事实相符。

2.2 三维速度算符矩阵元

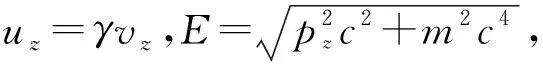
(11)

(12)

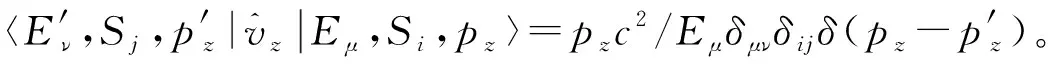
2.3 动力学方程

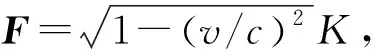
(13)

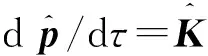
(14)

(15)

2.4 守恒量

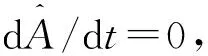
3 总结与展望

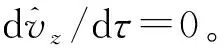
笔者并不期望通过使用相对论性矩阵力学在实际科学研究中取得突破，若使现有的量子力学理论变成一个更加完善的量子理论体系，这个新的相对论性矩阵力学无疑是一个很好的理论补充，可以使人们更全面地理解量子理论，同时希望有助于未来量子理论的研究。