Copula理论在金融管理领域中的应用概述

易文德， 黄爱华

（1. 重庆文理学院 数学与大数据学院， 重庆 永川 402160；2. 重庆文理学院 财务处， 重庆 永川 402160）

一、引言

众所周知， 具有相同相关系数的时间序列间的相依结构可能不同，或者说，不同相依结构的时间序列的相关系数可能相同。 金融时间序列间相依结构的复杂性和多样性不仅表现在相依分布的中部，而且还反映在相依分布的尾部。 相依结构会影响资产、资产组合的定价和风险测度，特别是在局部和某些极端情况下，相依结构对风险的预测起着决定性的影响。Boyer认为，在建立风险管理模型时仅仅考虑变量间的相关度（Degree of Dependence）是不够的，还必须考虑变量的相依结构（Dependence Structrue），并对Copula函数在风险管理中的应用问题进行探讨［1-2］。研究时间序列的相依结构不仅可以在相依程度上反映相关关系，还可以在相依的形态构成上反映相关的模式，以至更精细地刻画时间序列的相依特征。

由于金融市场不断涌现的典型事例，大量的理论和实证表明有效市场假说并非是实际市场运行机制的完美描述，许多金融资产风险度量分析技术的假设与实际有较大偏差，这就导致了有些分析技术的欠缺和局限性。 如在传统的风险管理理论中，通常假定资产收益服从正态分布，并采用Pearson的线性相关系数（Linear Correlation）作为资产相关性度量指标，众多研究结果表明，许多金融资产的收益具有明显的厚尾性，与正态分布假设相差较大；而当市场发生重大波动时，线性相关系数也无法反映出资产收益曲线的尾部相关特征。

相关性理论是研究资本证券市场复杂性问题的重要理论， 基于Copula理论的金融时间序列相依结构的研究是金融工程的重要研究课题。 它从金融时间序列自身的相依关系和时间序列之间相依关系的角度， 解释目前作为主流理论的有效市场假说所无法涵盖解释的随机现象，为市场动力分析提供了一种新的统计分析方法。

关于金融市场相依性的研究主要有三种方法：联合分布函数的方法、条件相关的方法和Copula函数理论的方法。 联合分布函数的方法通常应用联合正态分布和相关系数度量金融市场的相关性，线性相关系数对相关结构不能给予有效的分析，且要求边缘分布为椭圆形分布，而许多金融资产的收入序列并不满足这样的条件， 因此联合分布函数的方法具有很多局限性。 条件相关的方法在研究相关性时考虑了金融资产的条件信息，弥补了非条件线性相关的缺陷。 然而，Forbes 和Rigobon指出：条件相关系数在不同的条件下会产生很大变化，对相关性结果分析会产生误导而难以对结果进行解释［3］。 Copula函数方法是一种直接而灵活的相关性测度方法，它不仅可以测度相关的强度而且可捕捉相关的结构，能够适用于任何分布形式和测度非线性相关的情形，Copula函数方法已经成为相关性研究最有效的新方法。

1959年，Sklar定理的提出奠定了Copula理论的基础［4］。Joe和Nelson详细地介绍了Copula函数统计和数学方面的基本内容和性质［5-6］。Copula理论创立后，更多的是在数学性质等理论方面的研究。 由于计算技术的原因，其在应用方面研究的进展比较缓慢，在20世纪末才逐渐在各领域应用，特别是在金融风险管理中的应用得到了人们的重视，并迅速发展且取得了巨大的成果。 Embrechts等［2,7-8］最先把Copula理论引入风险管理中， 应用Copula理论研究金融、宏观经济和微观经济等数据的相依风险价值VaR，并研究Copula函数的参数估计、模型的评价方法。

基于Copula理论对时间序列建模的研究主要有两个方面： 一个方面是应用于多维时间序列模型，主要模拟随机向量Xt=（X1t，X2t，…，Xnt）′联合分布以研究各边缘序列间的相依结构，这导致了时变Copula函数的研究；另一方面是应用于模拟单个时间序列的观测序列（Xt，Xt+1，…，Xt+n）′的联合分布，以研究单个序列的观测序列的相依结构，这种应用引导人们考虑Markov过程和非线性的时间序列模型。 本文对Copula理论在金融风险管理领域中的应用进行归纳和概述，以期梳理Copula理论在金融管理中的研究进展和现状。

二、基于Copula理论的多维时间序列模型的研究

（一）多维时间序列模型

基于Copula理论的多维时间序列模型，主要是模拟随机变量Xt=（X1t，X2t，…，Xnt）′的联合分布以研究各边缘序列间的相依结构。Longin和Solnik［9］应用Gumbel Copula函数研究了资本市场的尾部相依关系，实证表明：拒绝多个资本市场的下尾服从多元正态分布，而不拒绝上尾服从正态分布，相关性与市场变化趋势相关而与市场自身的波动无关，熊市中相关性大于相对应的牛市中的相关性。 Patton［10-11］定义了条件Copula函数，结合GARCH模型和Copula理论分析外汇市场的相依关系时，研究了条件Copula函数参数的时变特征，刻画边缘分布应用了Engle［12］的ARCH模型和Bollerslev［13］的GARCH模型，参数时变形式的设定考虑了参数自身的滞后项和观测值滞后的关系。 Jondeau和Rockinger［14］考虑收益率的联合非正态分布和时变特征，其中包括了波动聚集性、非对称和肥尾特征，应用条件Copula函数研究了几个股票市场的相依关系及其时变性。 另外，Rodriguez［15］研究了条件Copula函数的结构转换模型，并应用该模型分析了金融市场的风险传染性。 Okimoto［16］研究了证券市场的非对称结构，发现证券收益率的相依函数在高期望、低波动状态时是显著非对称的，而在低期望、高波动状态时是对称的。 Lee和Long［17］把Copula理论和多元GARCH模型结合起来，构造灵活的Copula分布函数模拟多元GARCH模型回归的残差，GARCH模型能捕捉时间序列的时变相关关系， 而用Copula函数捕捉那些不能被GARCH模型刻画的无序列相关的残差之间的相依关系。

多元Copula函数模型构造：设随机变量X1，…，XN的Copula函数C（·，…，·;·）的密度分布为c（·，…，·；·），其边缘分布为Fn（·；·），边缘密度函数为fn（·；·），n=1，…，N，由Copula函数与联合分布的关系有：

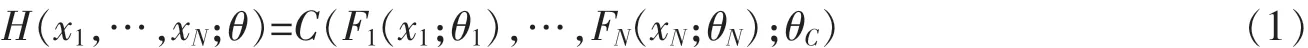
其联合密度函数为：

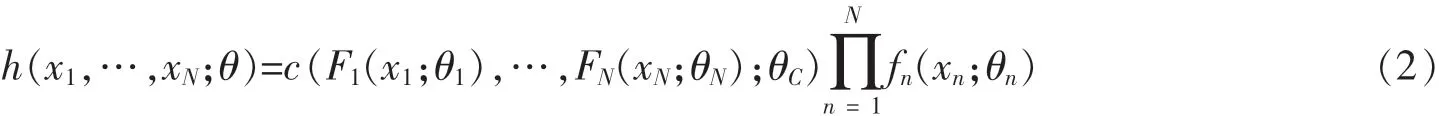
其中，θ=（θ1，…，θN；θC），样本（x1，t，…，xN+t），t=1，…，T。 对数似然函数表示为：

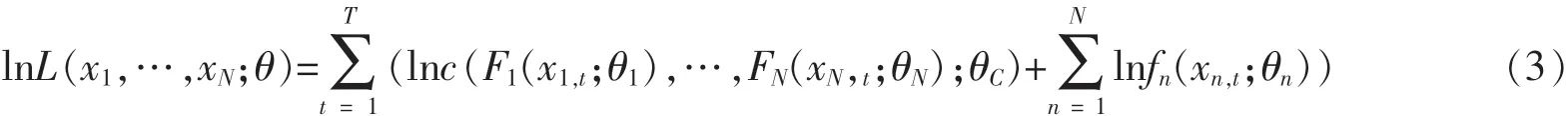
这样对模型参数的估计可以分步进行， 对于多参数模型来说可以提高参数估计的效能，节约模型的自由度，模型参数估计更具有优越性。

（二）单个时间序列模型

根据单个时间序列（Xt，Xt+1，…，Xt+n）′的观测序列建立Copula模型，以研究单个序列的时间上的前后相依关系。Darsow等［18］为一阶Markov时间序列建立了Copula模型，研究变量Xt和Xt+1之间的相依关系，并研究模型参数估计量的一些性质，给出了基于Copula的时间序列是Markov过程的充分必要条件。 Chen和Fan［19］研究了一阶Markov时间序列的半参数Copula模型的参数估计和模型误设情况下的模型选择问题，模型的边缘分布用非参数方法估计，而Copula函数设定为参数正态分布。 Ibragimov［20］把Darsow等的工作拓展到Markov链的高阶情形，并且新提出了一类Copula函数。 Beare［21］通过Copula函数的性质研究Markov时间序列的弱相依性，证明了时间序列的Copula函数尾部相依性会导致Markov 时间序列不满足标准混合条件。 Gagliardini 和Gourieroux［22］拓展了Engle和Russell的自回归条件持续时间模型，提出并研究了时间序列短期相依的Copula模型。 Ibragimov和Lentzas［23］对时间序列的长期相依关系进行了Copula函数模型探讨。

单个时间序列模型：设{Xt，t=1，2，…}由（F（·；θ），C（·，·；δ））生成的一阶平稳马尔科夫时间序列，其中F（·；θ）是连续的边缘分布函数，密度函数f（·；θ）是实数域上的Lebesgue测度；C（·，·；δ）是关于（Xt－1，Xt）的连续的Copula函数，密度函数c（·，·；δ）是（0，1）2上的Lebesgue测度，θ，δ分别是边缘分布和Copula函数的有限维参数。 由Sklar定理［6］：H（x，y；θ，δ）=C（F（x；θ），F（y；θ）；δ）是一个具有边缘分布为F（·；θ）的联合分布函数。 Joe［5］应用Copula函数模拟了马尔科夫时间序列的相依关系。 联合分布为H的平稳马尔科夫时间序列的转移概率密度函数可表示为:

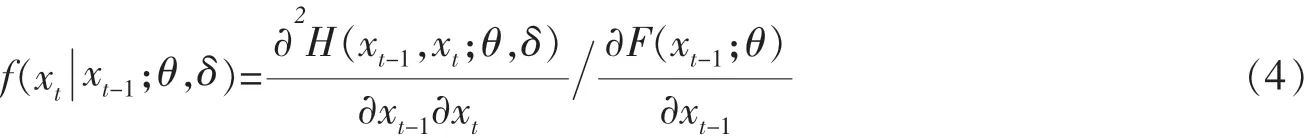
（4）式可以等价表示为：

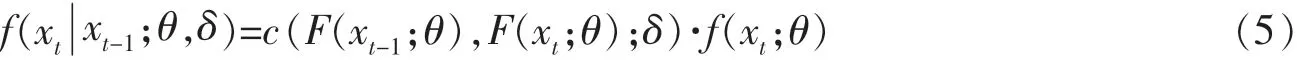
由（5）式可知，平稳马尔科夫时间序列完全由边缘分布和Copula函数确定。

（三）综合以上两类时间序列的相依关系模型

对于时间序列Xt和Yt组成的向量，这里有两类相依结构需要考虑：一类是单个序列时间上的相依关系，如Xt－1和Xt之间的相依关系；二是两个序列间的同期相依关系，如Xt和Yt之间的相依关系。 这两类相依关系都同时影响时间序列向量的相依关系，研究这两类相依关系的特性及其融合的方式，无疑是具有很大意义的。

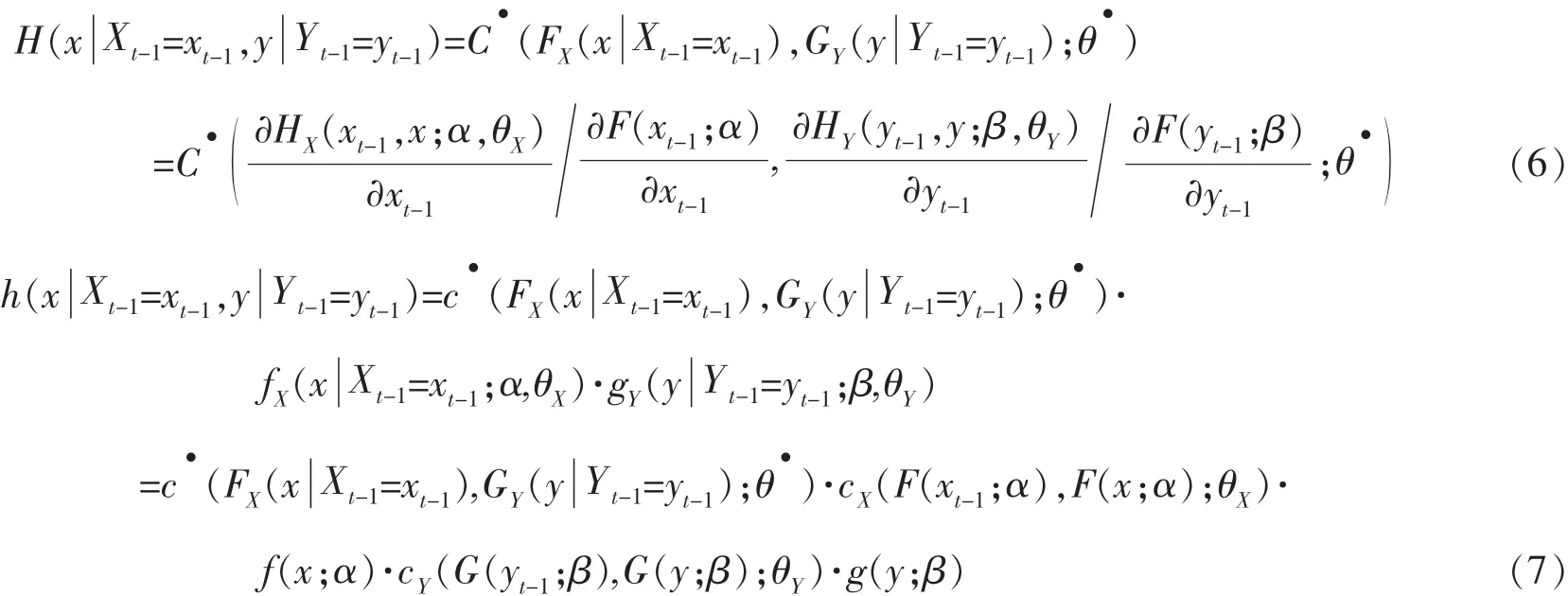
设时间序列Xt和Yt分别是一阶平稳的马尔科夫序列，F（·；α）和G（·；β）是连续的边缘分布Xt和Yt的边缘分布密度f（·；α）和g（·；β），二是Xt－1和Xt以及Yt－1和Yt的短期条件相依关系cX（·，·；θX）和cY（·，·；θY），三是Xt和Yt的同期相依关系c•（·，·；θ•）。这有利于模型参数的估计，估计模型参数时可以分阶段进行，便于模型的求解。

从（7）式可以看出，随机变量

三、Copula模型的估计与评价

多维时间序列Copula模型的参数估计有许多种方法，主要分为参数方法和非参数方法。

（一）完全参数模型

即条件边缘分布和条件Copula函数都是有限维的参数分布，可以应用极大似然估计方法，如果边缘分布、Copula函数可以分开，则参数估计可以分步进行，采用多步骤极大似然估计MSMLE （Multi-Stage Maximum Likelihood Estimation） 方法， 有时也称IFM（Inference Functions for Margins）方法。通过一元分布函数的极大似然估计方法估计边缘分布的参数，在此基础上再估计Copula模型的参数。 多步骤似然估计方法可以简化计算，降低或消除参数估计的维数问题。 Patton［11，24］应用多步骤极大似然估计MSMLE对多维时间序列模型的参数估计进行研究，考虑各时间序列的样本观测值的时间段不相同情况的估计效果，与一步极大似然 （1SMLE） 估计相比，MSMLE的估计效果没有比1SMLE的效果更差。 Chen与Fan［19，25］和Chen等（2006）［26］证明一阶平稳Markov时间序列Copula模型的半参数极大似然估计的一致性和近似正态性，并对模型进行了应用研究；而Abegaz和Naik-Nimbalkar［27］研究了一阶平稳Markov时间序列Copula模型的两阶段参数极大似然估计及其估计的一致性和近似正态性。 Prokhorov和Schmidt［28］研究了用面板数据对Copula函数进行准极大似然估计的稳健性、冗余性和有效性的实证分析。Kallenberg［29］研究用模型选择技术估计Copula函数密度问题，发现应用复杂的模型会产生较小模型误差，但会产生较大的随机或估计误差；而应用简单的模型则会产生较小的随机误差但会有较大的模型误差。 Fantazzini［30］研究t-Copula的三阶段半参数估计以及估计的近似性质， 并分析了这种估计的优缺点。 Yi和Liao［31］考虑时间序列的同期相依关系和短期相依关系，建立了一阶平稳Markov时间序列Copula模型， 提出模型参数的三阶段准极大似然估计方法3SPMLE （three-stage pseudo maximum likelihood estimation），并研究3SPMLE参数估计的一致性和近似正态性。 Autin等［32］用小波方法研究多维Copula密度函数的估计问题，并提出了估计的算法和用模拟的方法评价了估计方法的性质。

（二）非参数估计方法

Genest和Rivest［33］、Capéraà等［34］对多维随机变量的Copula模型进行了非参数估计方法的研究，而Ibragimov［35］研究了单个时间序列Copula模型的非参数估计方法。Chen等［36］提出基于置信区间（Confidence Intervals）的经验似然方法（Empirical Likelihood）估计Copula函数模型，通过与Bootstrap方法的对比进行了实证和模拟研究。

在实际应用中通常要检验模型是否充分反映经济数据的实际特征，因此模型的评价在经济应用研究中是非常重要的内容。Copula模型的评价主要有两类：一类是在几个模型中选择最好的模型，这种检验评价方法是用模型的经济标准或统计标准加以比较，如似然比检验、信息准则AIC或BIC(Akaike or Schwarz’s Bayesian Information Criteria)。 Diebold 等［37］对Copula模型的分布密度的选择评价问题进行了研究，Chen和 Fan［38-39］研究了Copula模型的分布密度的评价和半参数时间序列Copula模型的似然比检验问题，Abegaz和Naik-Nimbalkar［27］研究了一阶平稳Markov时间序列参数Copula模型在误设情况下似然比检验问题。 另一类是评价一个单独的模型是否充分拟合了数据，如构造某种统计量，在一定的置信水平下比较统计量与临界值的大小以决定模型的拟合优度，如χ2检验，“Hit”检验等。 Malevergne和Sornette［40］研究了高斯Copula模型的拟合检验，Panchenko［41］研究了时间序列模型的拟合检验，Scaillet［42］研究了独立同分布随机变量Copula模型的拟合评价，Genest等［43］研究了时间序列基于概率积分变换方法Copula模型的拟合检验问题。

四、Copula理论在金融和经济领域中的应用

Copula理论在金融和经济领域中的应用主要集中在风险管理、期权定价、组合投资、信用风险和金融市场的传染性等方面。

（一）在风险管理领域

目前主流的风险价值指标为VaR（Value at Risk）, 而大量的研究证明许多金融时间序列具有高峰厚尾性而不服从正态分布。因此，在正态分布假设下计算的VaR值，常常会低估实际的风险，而在低估的风险值下进行风险管理运作，可能会使金融机构遭受巨大的损失。 为了更准确有效地测度资产的风险价值, Hull 和White［44］研究变量的非正态假设情况下的VaR， Embrechts等［8］应用Copula理论研究组合资产的风险价值VaR；Rosenberg 和 Schuermann［45］应用Copula理论研究市场的综合风险问题，他们认为研究风险时必须同时考虑市场风险、信用风险和操作风险。 McNeil等［46］和Alexander［47］对Copula理论在风险管理中的应用问题做了较详细的阐述，从多角度分析Copula理论在金融风险管理中的建模应用问题。 Huang［48］实证研究了应用条件Copula-GARCH模型估计计算组合资产的VaR的方法，认为估计组合资产的VaR时Copula模型比传统的模型更好。 Fantazzini［49］研究边缘分布和Copula函数都为误设情况下VaR估计的蒙特卡罗（Monte Carlo）方法，指出Copula误设对VaR估计的影响主要取决于相依的程度。 Chollete等［50］应用多元Copula转换模型研究了金融资产的相依关系，认为Copula模型能模拟金融市场的相依结构，边缘分布的选择对Copula建模有重要影响。

（二）在期权定价领域

Cherubini等［51］比较详细地介绍了Copula理论在期权资产定价中的应用研究，Zhang等［52］应用时变Copula模型研究了GARCH过程的期权定价问题， 实证认为期权定价的动态Copula模型优于静态模型。 Lai等［53］应用Copula-门限GARCH模型研究了五个东亚国家的现货和期货市场的最优套期保值模型，研究认为由Gaussian 或混合copula模型所构造的对冲比率（hedge ratios）更为合理。 有关Copula理论应用于衍生资产定价的研究还有Rosenberg［54］和van den Goorbergh等［55］等，他们从不同的角度研究期权价格相依性的模型拟合问题。

（三）在组合投资领域

一般认为组合资产的效用函数是二次的、服从多元椭圆形分布，在决定最优组合资产的权重时，仅考虑资产价格序列的一阶矩、二阶矩和线性相关系数。 然而，大量的研究证明组合资产的上述假设是不成立的，因此，在做最优组合资产投资决策时，需要设定组合资产的条件联合分布。 Patton［56］应用Copula理论，结合资产的峰度和偏度，研究两个资产的投资组合问题，并分析组合投资在熊市和牛市情况下的相依关系问题；而Garcia和Tsafack［57］的研究分析了四类资产，其中包括股票和债券资产，同类资产有较强的相关性，特别是在非对称的情况下，而资产和债券间的相关性较弱。 Sak等［58］应用t-Copula模型研究资产线性组合的尾部概率有效模拟计算问题，t-Copula模型捕捉资产对数收益率之间的相依结构，而假设边缘分布服从广义二次曲线分布。

（四）在信用风险领域

Li［59］最早把Copula理论应用于信用风险管理中，定义了两个信用风险资产的违约相依关系，探讨应用Copula理论研究违约相关问题的方法。 Giesecke［60］应用Copula理论研究不完全信息状况下的违约相关性问题， 一个公司的违约会导致投资者对相关资产价格进行重新评估，违约具有传染性。 Chen等［61］从日本证券市场选择43家公司研究信用违约收益与证券收益率分布的峰度之间的相依结构，认为Gumbel函数最适合描述它们之间的相依结构，认为在低信用等级时信用违约收益对信用转移风险更敏感。 He和Gong［62］构造基于Copula理论的条件风险价值CVaR (Conditional Value-at-Risk)模型以刻画市场和信用风险的相依关系，研究结果显示，如果忽略信用风险，公司股票的相依风险会低估。

（五）金融波动传染性研究

金融波动传染性是金融市场普遍存在的现象，一个市场的剧烈波动或危机会导致其他市场出现剧烈波动或危机，1997年的亚洲金融危机和2008年美国次级债贷款危机就是例子。 在危机时期和非危机时期，市场的相依程度以及相依结构是不相同的。为研究这个问题,Baur［63］研究了金融市场的波动溢出和相关性； Granger等［64］研究了二维时间序列条件分布的公共因素，收入与消费之间的影响因素是在边缘分布上而不是在Copula模型所刻画的相依关系上；Hu［65］提出用混合Copula函数对金融数据进行分析可以较好地捕捉金融变量的尾部相依性；Hu［66］应用条件时变Copula模型研究中国股票市场与美国股票市场的相依关系，实证认为：时变相依模型不一定总是优于常变量模型，在有些时间段内，上尾的相依程度比下尾的相依程度明显更高，中国股票市场具有相对的独立性，中国市场与美国市场的尾部相依关系要强于与其他国家股市的相关性；Jondeau 和Rockinger［14］应用时变Copula模型研究四个主要国际股票市场的相依关系；Rodriguez［15］应用混合Copula模型研究东亚股票市场与拉丁美洲股票市场在金融危机时的风险传染性，建立了Markov转换的Copula模型；Ning和Wirjanto［67］研究东亚国家6个新兴股票市场的指数与交易量尾部的相依关系，实证发现这些市场的指数与交易量尾部相依关系是显著、非对称的，特别发现指数的极端上涨与极端大的交易量相联系，但是没有发现指数的极端下跌与极端大或极端小的交易量有联系。 Ning［68］应用Copula函数研究资本市场与外汇市场的相依结构。

五、国内研究现状

国内许多学者应用Copula模型实证研究金融市场中多个不同方面的现象和问题， 取得了丰富的研究成果。张尧庭［69］从理论上探讨Copula在金融管理方面应用的可行性，分析了各相关性指标的优缺点；韦艳华、张世英［70］等用Copula-ARCH 模型研究上海证券市场中几个板块间的相关性，讨论Copula-ARCH类模型的构建，并应用于金融市场的风险分析中；史道济等［71-72］应用Copula理论研究沪深股市的相依性以及相依风险价值VaR；何其祥等［73］研究股指期货的投资组合风险；刘志东［74］结合GARCH-EVT模型研究资产组合选择模型以及模型的混合遗传算法；刘晓星和邱桂华［75］基于Copula-EVT模型研究我国股票市场流动性调整的VaR和ES风险指标；詹原瑞等［76］应用Copula函数族研究信用违约互换组合定价问题；吴恒煜等［77］研究我国国债利率期限结构，发现Gumbel Copula和混合Copula能较好地描述1年期和10年期国债利率的结构；童中文等［78］、李建平等［79］也对信用风险和违约风险的相关性进行了研究；叶五一等［80-81］应用Copula函数研究风险价值和美国次级债金融危机的传染性；杜子平等［82］研究基于“藤”结构的高维动态Copula模型的构建。 还有一些学者，如傅强、朱世武、陈守东、李秀敏、罗付岩、王玉刚、易文德、张明恒、蔡霞、胡心瀚等，也应用Copula函数对金融市场的相关性作过一些探讨［74,83-91］。

同时， 近年来国内若干课题组对Copula理论及其在金融领域的应用方面也进行了卓有成效的研究，如北京航空航天大学李平教授的“基于动态Copula的多元信用衍生产品定价”和“离散时间不完全金融市场中基于Copula的多资产期权定价研究”； 江西财经大学吴恒煜先生的“基于Copula的多重基于资产信用衍生品定价的蒙特卡罗模拟方法研究”； 天津科技大学杜子平先生的“动态Copula模型的构建及其在金融领域的应用研究”和“时序非线性相依Copula分析建模及金融领域应用研究”。 还有许多国内学者也进行了相关研究，在此不一一列举。

六、存在问题分析

截至目前， 运用Copula理论探索金融时间序列的相依关系而进行的风险管理还存在以下三个方面的问题：

一是模型相依关系的单一性问题。 现有的Copula函数模型都只考虑金融时间序列间的同期相依结构或时间序列的短期相依结构。 金融时间序列的相依关系主要有两类：一类是金融时间序列之间的相依关系，即时间序列的同期相依关系；另一类是单个时间序列的短期相依关系。而已有的这些Copula相依模型都只是考虑了单方面的相依关系，而没有把这两类相依关系同时考虑进去。

二是边缘时间序列波动性的拟合问题。 单个时间序列的波动一般用ARCH类模型来描述，现有模型一般只考虑边缘时间序列波动的一阶矩和二阶矩的影响，而对金融时间序列的高阶矩影响没有考虑，也未进行系统分析。

三是非线性相依结构模型的描述问题。 虽然Copula理论作为研究随机变量间非线性相依关系的一种更为广泛和灵活的统计方法而受到关注，但建立一个充分描述非线性相依结构模型仍然是困难的。