寻思考路径 促思维进阶①——试卷讲评课的教学思考

宋秀云

(江苏省新海高级中学 222006)

考试中学生的解题状况，能更准确地折射出学生的学习情况，能提出教学中需要调整、关注的问题.通过对考试过程中学生答题情况的研判，选择典型试题的学生解答过程，精心设计试卷讲评课，对于提高学生解题能力，理解数学的本质，进阶学生的思维非常重要，是高中数学复习阶段教学中特别重要的教学环节.然而，在了解学生的答题情况之后，根据获得的信息，如何精准定位学生遇到的困难，找到突破困难的方法？如何对试题再思考，引导学生有序探究试题不同的处理方法？如何完善学生的知识系统与思维系统，通过试题讲评课引导学生对知识、方法作进一步的归纳，站到学科思想的高度认识、理解所学内容？这些问题是试卷讲评课中的困境，本文以一道试题为例，探索试卷讲评过程中上述问题的解决方案.

1 研：明学生考情

试题已知抛物线y2=2px(p>0)上三点A(2,2),B,C，直线AB,AC是圆(x-2)2+y2=1的两条切线，则直线BC的方程为( ).

A.x+2y+1=0 B.3x+6y+4=0

C.2x+6y+3=0 D.x+3y+2=0

题目条件简单，很容易找到解决问题的方法，设计出求解的思路.即由直线与圆相切，确定直线的斜率，点斜式写出直线方程，与抛物线联立，求出点B,C的坐标，进而写出直线BC方程.但是数据似乎不是很友好，耗时耗力.

我省是教育基础比较发达的省份，全省高三学生答题情况为：A.16.32%； B.37.42%； C.28.84%； D.16.73%.正确率仅为37.42%.某中学为全省20所示范高中之一，该学校理化班学生仅有53%学生得到正确结果，历史选科班级学生仅有28%得到正确结果.

为什么会出现这种情况？我们组织教师对该试题的目标定位进行分析，对我校600名学生的答题过程进行数据处理，对学生的解题方法与错误进行聚类分析，进而根据学生的思维层次进行比对，清晰地厘清学生在解题过程中的思维水平、思维障碍.

试题讲评课需要教师做好充分的准备.老师需要收集学生答题的第一手资料，包括学生最容易想到的方法、遇到的困难、错误的类型、知识与能力的缺陷等等，根据这些信息以及老师对试题的理解，思考试题讲评的定位，在此基础上再分析收集的材料，根据学生的思维习惯，确定讲评顺序，做到有序推进、有的放矢.

2 讲：寻思考路径

这是一道典型的看上去不难、而动手却不容易算出来的题目.试题评讲的时候，一方面要强调、鼓励学生将第一时间想到的常规方法静心、耐心做到底，体会运算过程中算理、算法的调整，通过自己的努力“硬”解出点的坐标，练就应对解析几何问题的运算能力；另一方面，也要充分挖掘试题隐藏的条件与结果之间的联系，算思结合，曲径通幽，优化解决问题的方案，并能触类旁通、举一反三，进而提升对解析几何问题的处理能力，生成智慧，提升素养.

怎样才能迅速、准确地寻找到解决问题的有效方法与路径，最为重要的是学生对解决问题的路径进行透彻的分析，解决问题的路径清晰了，学生的思维才能清晰，才能选择合理而简洁的解决问题的方法.

3 评：促思维进阶

根据数据分析的考情研判、试题解决过程的路径分析，结合本班学生的具体情况，对本道试题的讲评，预设了五种不同的解决方案，根据学生的解答情况，结合学生的思维过程安排讲评顺序.

学生思维进阶分析图

在讲评时，笔者把学生最容易想到的方法先讲评，在此基础上调整思考角度、提升思维层次，本题的讲评顺序依次为：直接求出B、C两点坐标，利用两点式写出直线方程；寻找直线的斜率和直线上一点坐标，根据点斜式写出直线方程；构造齐次式，根据一般式写出直线方程；利用斜率“同构”写出直线方程；利用坐标“同构”写出直线方程.

讲评一：方程组思想，求出点B,C坐标，写直线方程(两点式方程)

由A(2,2)在抛物线上得抛物线方程为y2=2x,

由题意切线AB,AC的斜率均存在，设直线AB:y-2=k(x-2)，即kx-y-2k+2=0.

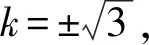
由点A(2,2)及一元二次方程根与系数关系，

代入直线AB方程得B点坐标为

从而得到直线BC方程为3x+6y+4=0.

点评以直线的两点式方程为突破口，常规方法，非常重要.朴素、直接、易操作，但数据复杂，运算易错.解题过程中，减元的时候注意到抛物线方程的特点，消x更好一些.另外，在解一元二次方程的时候，注意到点A的纵坐标是方程的一个解，利用两根积求另一个根，也能减少一定的运算量，并提高准确率.

讲评二：点差法，通过寻找BC直线的斜率与线段BC的中点坐标得到直线方程(点斜式方程)

设B(x1,y1),C(x2y2)，

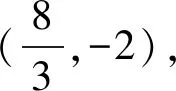
从而得到直线BC方程为3x+6y+4=0.

点评以直线的点斜式方程为突破口，通过点差法，回避硬解点坐标，充分利用点在抛物线上这一特征，寻找直线的斜率与坐标之间关系，大大降低了运算量.点差法在解决直线与圆锥曲线相交问题中，特别是中点弦、对称等问题中使用非常频繁.

讲评三：构造关于直线AB，AC的斜率的一元二次方程，利用根与系数的关系(一般式方程)

注意到直线BC一定不过点A，设直线BC的方程为m(x-2)+n(y-2)=1.

又注意到kAB+kAC=0,kAB·kAC=-3,

由y2=2x构造齐次式：

(y-2+2)2=2(x-2+2),

(y-2)2+4(y-2)-2(x-2)=0,

(y-2)2+[4(y-2)-2(x-2)][m(x-2)+n(y-2)]=0,

(1+4n)(y-2)2-2m(x-2)2+(4m-2n)(x-2)(y-2)=0,

等式两边同除以(x-2)2，得

显然1+4n≠0，kAB,kAC为上述方程的两个根，由根与系数的关系得

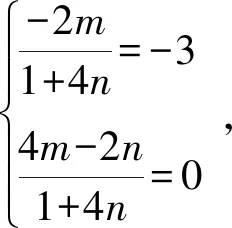
所以直线BC方程为3x+6y+4=0.

点评以直线的一般式方程为突破口，通过齐次式构造关于斜率的一元二次方程，借助两条切线的斜率之和与斜率之积为定值，确定直线方程.2020年山东卷的解析几何题、2020年全国一卷的解析几何题，均可以使用类似方法解决.

讲评四：借助斜率“同构”，设而不求

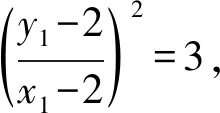
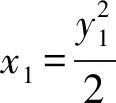
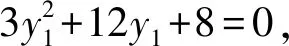
得3x1+6y1+4=0，同理3x2+6y2+4=0，

所以点B(x1,y1),C(x2，y2)在直线3x+6y+4=0上，两点确定一条直线，所以直线BC方程为 3x+6y+4=0.

点评本题直线AC、BC地位一样，通过两点坐标表达直线AC的斜率，借助抛物线上点横纵坐标之间的联系，得到x1,y1所满足的关系，从而同构x2,y2所满足类似关系，最终确定直线BC的方程.过圆外一点引圆的切线，如果切点分别为P,Q，也可以通过类似方法求出切点弦PQ所在直线方程.

讲评五：借助坐标“同构”，设而不求

2x-(b+c)y+bc=0，

又A(2,2)，得到直线AC：

2x-(2+c)y+2c=0，

因为直线AC为圆(x-2)2+y2=1的切线，

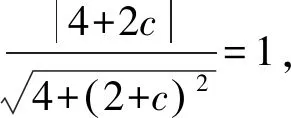
同理3b2+12b+8=0；

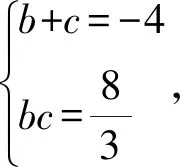
所以直线BC的方程为3x+6y+4=0.

点评根据抛物线上点坐标的特点，设出B、C两点坐标，用坐标写出BC直线方程，发现方程中出现待定的b+c,bc，再根据A的坐标写出直线AC的方程，再借助直线与圆相切的条件得到c需要满足的条件，同构得到b需要满足的条件，发现b,c为方程3x2+12x+8=0的两根，设而不求轻松得到直线BC的方程.

4 思：以学生为本

试卷讲评课是在学生完成考试之后，教师根据学生反馈的信息，对试卷进行剖析与点评.试卷讲评课要真正以学生为本，以学生的思维发展为本，带领学生厘清思考路径，完善知识结构，提高解题能力，掌握学习方法作为教学目标，更要充分挖掘试题的育人功能，将有序思考、突破困难、激发潜能、进阶思维作为重要的教学目标.

4.1 试卷讲评课要带领学生突破困难,提升能力

方法一无疑是最直接、最有效、最朴素的方法，是面向全体学生的方法，是每位同学必须尝试去用的方法.教学过程中，笔者要求所有学生必须亲历解题过程，最终真正算出点坐标，写出直线方程.解析几何就是用代数的方法解决几何问题，不能回避运算，所以作为老师更不能为了寻找更优解法，而将常规方法蜻蜓点水，一笔带过.常规方法不能只是用眼睛看看、用嘴巴说说，必须动手真正操作、真正算到底.当然，在运算过程中还是需要引导学生注意细节，如：联立方程之后如何减元，减掉哪个元；如何解系数较为复杂的一元二次方程，是求根公式，还是十字相乘，亦或是韦达定理；如何类比点B坐标准确得到点C的坐标等等.老师带领学生一起将最先想到、最易想到的常规方法的解题过程不断优化，才是在学生思维的最近发展区提高学生解题能力的关键所在.

4.2 试卷讲评课要带领学生探究方法，深度理解

试题讲评时遇到好的素材，必须好好把握，精心设计，挖掘试题的价值，充分发挥试题的作用，促进学生深度学习与思维进阶.本题就是难得一遇的“好题”，一方面，条件简单，学生上手容易，不畏惧；另一方面，思考的角度，理解的深度，又体现了学生思维层次的高度.讲评课引导学生从问题要求的结果入手，请学生思考如何确定直线方程，有序展开求解.选择两点式、点斜式、还是一般式，选定方程形式之后，教师顺势而为，继续引导学生发现:两点式需要利用方程组的思想求出点B,C坐标；点斜式关键是如何不解B、C两点坐标确定直线的斜率，借助B、C两点都在抛物线上的特点，将斜率用BC的中点坐标表达，从而将求两点的坐标简化为只求BC中点的坐标即可；一般式则是注意到直线不经过点A以及切线的斜率和、斜率积为定值，借助齐次式构造关于AB、AC斜率的一元二次方程，实现了不求点坐标的目的.三种方法，三个角度，三种方程形式，经历了从求两个点的坐标到求一个点的坐标，再到不求点的坐标这样的思维优化，学生亲历寻找直线方程的全过程.试题讲评课就是要教会学生如何寻找，如何转化，如何一步步实现条件与结果的对接，学会有序思考，找到解决问题的方法.

4.3 试卷讲评课要带领学生举一反三，生成智慧

如果某种方法只是为了解一道题而存在，那它一定不是最有意义、最有价值的方法.探究过程中呈现的方法应该能触类旁通，举一反三，解决一类问题.如果试题讲评课只是风干的教条、只采用记忆，只追求在特定的情境下回忆，是不可能促进智慧的生成与发展的，是低级的学习行为.做到触类旁通、举一反三能使知识理解得更为透彻，方法领悟得更为得心应手，能体会到方法背后深远的思想价值.方法四与方法五都是设而不求，利用“同构”的想法，回避繁琐的运算轻松解题的.本题“同构”的是方程、是等式，“同构”的思想方法能否运用到函数、不等式中呢？答案是肯定的.

比如，已知a<5且ae5=5ea，b<4且be4=4eb，c<3且ce3=3ec，则( ).

A.c

C.a

再比如(2020·新全国1山东)，已知函数f(x)=aex-1-lnx+lna．第2问中：若f(x)≥1，求a的取值范围．

利用指数对数的运算可将f(x)≥1转化为eln a+x-1+lna+x-1≥eln x+lnx,

令g(x)=ex+x,上述不等式等价于g(lna+x-1)≥g(lnx),注意到g(x)的单调性，进一步等价转化为lna≥lnx-x+1，令h(x)=lnx-x+1,利用导数求得h(x)max，进而根据不等式恒成立的意义得到关于a的对数不等式，解得a的取值范围.

试题讲评课通过这样的延伸与拓展，学生能更深入地理解何时可以“同构”、如何进行“同构”、“同构”之后怎样解决问题，如此，那些“别人家孩子的方法”才不是用来赏析的，才能真正为自己所有，成为自己的智慧.

4.4 试卷讲评课要带领学生有序思维，转层进阶

普通高中数学课程标准指出,让学生初步学会用数学的思维方法去观察、分析现实社会，去解决生活中和其他学科学习中的问题，增强应用数学的意识.学生有序思维能力的培养，对学生分析问题、解决问题能力的提高发挥至关重要的作用.有序思维，就是在数学问题的解决过程中，思维沿着由低到高、由浅入深、由远及近不断优化、逐步向前推进，直至更合理、更有效地解决问题的思维活动.这种思维活动能够使学生分析问题有条理，能够优化学生的思维过程，使学生在掌握基础知识、基本方法的同时理解知识发生、发展的具体过程，有利于促进学生思维品质的提升.

试题讲评要真正与学生思维层次、思维类型相匹配.教学中教师要寻求与学生思维水平匹配的讲评方式，这就要求我们把思维路径理清楚，把学生解题过程中思维层次理清楚，找到学生在思维转层时出现的障碍，进而贴近学生的思维层次与过程进行讲评.

对试题深入研判，根据学生的思维习惯确定讲评的先后顺序，为学生提供能够触类旁通的“解题路径”，使学生感受分析过程从“雾里看花”走向“剥茧抽丝”.讲评过程中教师适时进行方法的提炼与推广，这是一种复杂的思维活动，是一种有序思维的层层推进，这种思维活动能让抽象的“概括”变得具体可感、可观、可操作，解题路径更为清晰.有序思维调整和改善学生的思维方式，为数学行为的有序发展提供了潜在的加速度，在这样的有序思维训练中促使学生的高阶思维能力悄然生长.