数学解题需要套路吗

彭达浩 李 祎

(福建师范大学数学与统计学院 350108)

问题是数学的心脏，解题是数学的特点．“要学好数学，提高解题能力，那就必须要多做题”，这一点似乎已成为当代数学家与教育家的共识[1]．如今无论是教材还是教辅资料，均包含大量的数学习题，这些习题不仅能巩固知识，还能提高解题能力．同时也表明，学生解题能力的提高并非一蹴而就的，而是一个长期累积的过程．在此过程中，许多中学教师将目光锁定在解题“套路”上，试图在千变万化的解题方法中，寻求一把以不变应万变的钥匙．然而，数学解题存在套路吗？数学解题需要套路吗？解题套路一定威力无穷吗？

1 “套”以为优

“套路”是指在解题过程中，使用程序化的解题步骤进行数学表达的方法．单墫教授在《解题研究》一书中将数学问题分为两类，其中一类便是常规题，即有固定套路可循，可以借助套路模板解决的问题[1]．学生面对此类题目，并不需要有太多创造性的想法，只需在题目中找寻关键词，然后套入合适的模板即可解决问题．像这种固定化的数学套路在教学中屡见不鲜，如列方程解应用题的过程可简化为“审、设、列、解、验”的固定程序；又如基本不等式问题中“一正，二定，三相等”的口诀等．总体而言，借助这样的解题套路，学生可以快速获得问题的答案．

从斯根普的研究来看，上述程序性的解题模式就是将学生对知识的理解归于工具性层面[2]．从工具性理解的角度来看，解题套路易使学生对新知产生简单的记忆和应用，为学生解决问题提供了“易上手、易效仿、易记忆”的机会，为学生探索标准性问题的答案提供了捷径，促使学生逐步形成“理解-记忆-应用-再理解”的良性循环．此外，由于解题套路可以帮助学生快速获得问题答案，并逐步使学生建立起愈发稳固的自信心，故而能够在一定程度上提升学生的学习成绩，促使教学获得立竿见影的效果．

从行为主义的视角来看，学习是刺激与反应的联结，而联结的稳定程度和强弱程度又受训练次数的影响．因此，学生在“题海教学”下获得的解题套路训练，将使得自身的数学技能愈发强健，数学技能逐步由“自发执行”转向“自动执行”．学生对知识的理解将演变为具体的解题步骤．因此解题套路有助于引导学生踏上一条提高学习成绩的“正轨”，进而在学习成绩上获得立竿见影的效果．

2 熟能生“笨”

习惯使用解题套路的学生，往往已熟悉解题步骤．在思想上，学生会误认为“学习知识的目的在于获得一种在相似情境下，解决同类问题的技能”，自身的心理也会对解题套路产生强烈依赖．在行为上，学生会基于条件反射的作用，习惯性地将某种固定不变的方法应用于处理各式各样的情况．而这种方法是一种万能的良策吗？

所谓“万能”是指学生不论面对何种问题时，均可使用具体的解题套路解决问题．但在现实中，存在不少数学问题无规律可循，不能对其简单地套用原来的解决方法．这便是单墫教授提到的另一种问题类型，即非常规、结构不良的题型，这类题型往往没有固定的套路可循，需要解题者发挥自己的创造性思维[1]．此外，还有部分问题源自对常规题的合理变式，此类问题虽外形酷似常规题，但其解决方法却与常规题的解题套路大相径庭．

例如在基本不等式的最值问题中，学生会习惯性地对某类最值问题的解法产生较强的心理倾向，进而忽视问题变化所带来的解题策略变化，具体如图1所示．

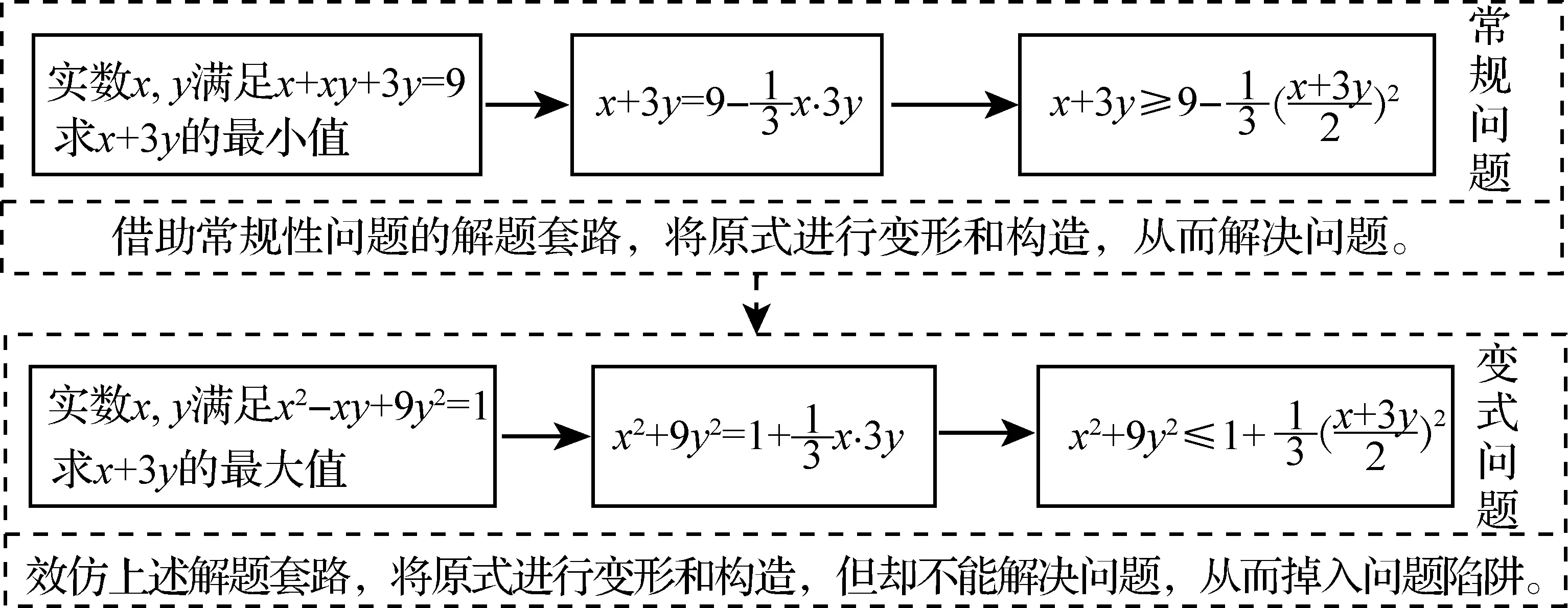
图1

上述变式题目在题型特点上并非以往的套路型问题，但学生普遍对此类问题形成了思维定势，习惯于不假思索地将解题方法进行生搬硬套．倘若常规性问题的解题套路成为了解决问题的习惯性方式，那么学生便难以跳脱解题套路的固有模板，去寻求新的思考方式．当然，对于更为一般的非常规性问题，学生在陌生的问题情境中更会感到无从下手．

根据格式塔心理学家的研究，用固定的程序解题与有意义的解题存在明显区别，后者旨在厘清问题本质的基础上解决问题．故学生一味地运用解题套路只是在强化自身所掌握的解题程序，忽视对问题本质的探索将会阻碍学生数学思维的锻炼与提高．此类现象表明套路虽可为学生的解题带来捷径，但学生对解题套路的过分熟悉，会使得自身在面对形形色色的问题时表现出笨拙的特点．

至于“良策”，即指在解决问题时所应用的好办法．就常规问题而言，虽然应用套路可以解决问题，但其一定是解决该问题的最佳方法吗？显然未必．但由于学生普遍能娴熟地应用解题套路，习惯于将数学解题视为无意识的、重复操作的过程，导致学生在面对许多可以一题多解的题目时，忽视了对最优解法的探寻．在此过程中，学生扮演着解题套路的搬运工，只知对解题步骤进行回忆和模仿，忽视对问题进行深层次的探究与创新．因此，学生对解题套路的熟悉致使其不知灵活变通，由此产生熟能生“笨”的情况[3]．

比如在解三角形问题时，学生会面临使用正弦定理或余弦定理的选择．学生通过对问题的观察，根据问题的表征，从而习惯性地作出判断．基于这样的解题套路，学生或许能够解决问题，但却无法获得更为简便的方法，具体如图2所示．

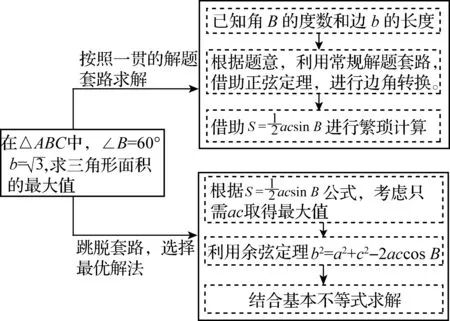
图2

在这一问题的解决中，学生若习惯于使用套路解题，则会将问题复杂化，从而不能将其迅速而精准地求解．久而久之，学生在解题的灵活性方面就会弱化，逐渐将自身局限于解题套路的思维半径之内．换句话说，学生盲目地使用解题套路，甚至会使学生走上解题“弯路”．其主要原因就在于，学生往往只关心用套路“怎么做”，常常忽略思考“为什么这样做”，以及套路之外“还可以怎么做”．这既不利于学生在陌生情境中开展知识迁移，更不利于发展学生的数学能力．

3 “思”则有路

针对以上对解题套路的优缺点分析，教师应辩证地看待套路教学，并贯彻因“题”施教的原则，从而有效提高学生的数学解题能力．以下从解题套路、思路及思想等三个层次进行分析．

3.1 探索套路，知其然

“套路”在数学教学中被定义为处理某一类问题的方法和技巧，这些方法与技巧往往被描述为一系列的操作步骤，其最大特点便是程序性和可操作性，因此易被学生所掌握和应用．在解题套路的引导下，学生能够对问题“知其然”，明确“如何做”，从而快速地解答某一类型的问题．

基于解题套路的优点，教师在日常教学中，应针对部分内容开展解题套路教学．根据建构主义学习理论，教师是教学过程的组织者，应充分发挥学生学习的主观能动性，因此在解题教学中，教师应转变自身角色，由“讲解套路”的传授者，转变为引导学生“探索套路”的组织者．在具体教学中，教师应围绕问题为学生创造观察、联想、抽象问题的机会，从而使学生在手脑并用的过程中，感悟解题魅力，提炼出解题套路．

如图3所示，在提炼出解题套路之后，教师还应为学生创造精熟套路和巩固套路的机会.为让学生精熟套路，教师需为学生设计丰富多样的同类问题，让学生从回忆套路的思维层面逐渐转向模仿套路的行为层面.记忆是要求学生能够流畅而完整地输出信息，为开展具体的实践活动提供前提保障，而模仿则是解决问题的开始．巩固套路则是基于“木桶效应”原理．由于解题套路是一系列的操作步骤，故解题的每一环节都十分重要．倘若学生在某一解题环节上薄弱，那么学生也不易借助套路而成功解决问题．因此，教师需在学生应用套路解题的过程中，对学生的行为进行及时纠正，以此帮助学生巩固解题套路．

图3

3.2 凝练思路，知其所以然

“授之以鱼，不如授之以渔”，其虽深深地影响着教师的日常教学，但教师绝不能将“渔”单一地视为“解题套路”．大量的解题套路虽可提高学生的解题能力，但其绝非学生解决问题的万能之策．根据以上对解题套路的不足与缺陷的分析，并考虑到学生需要面对形形色色的问题，故教师对学生解题能力的培养不能停留在套路水平，应让学生在“知其然”的基础上，做到“知其所以然”．一方面，教师在与学生共同提炼套路的过程中，应不断引导学生理清解题技巧与方法的缘由，明白相关解题套路的内在原理．另一方面，教师还应锻炼学生将问题与套路进行匹配的能力，学生能够基于问题做出精准判断与选择，从而凝练出解题思路．针对后者，举例分析如下．

本题要求学生首先要弄清不等式的性质，从而得出函数f(x)的最小值恒大于等于0，进而利用函数单调性求解最值．在此过程中，学生还应注意导函数在极值点处的导数为0，即发现a为极值点，从而开展分类讨论．因此，教师为帮助学生凝练解题思路，需在解题过程中层层设问，逐步引导学生根据问题选择正确的知识与方法，并对方法的可行性做出判断，进而在大脑中勾勒出解题思路．为让学生“知其所以然”，可设计如图4所示的教学过程．

图4

3.3 领悟思想，知其何以所以然

通过让学生亲历解题，探索解题套路，从而使学生在套路中生长出解题思路．这样的教学模式虽为学生提供了强化解题能力的途径，但其终究是一种以知识为基础，以方法为手段的教学，其并不能满足学生的发展需要．因此，学生解题的目的也不应局限于借助知识和方法获得答案，更应在问题解决的过程中，埋下套路的种子，生长出思路的茎叶，从而孕育出思想的花朵．数学思想是数学的灵魂[4]，是学生将知识融会贯通的基础，是学生提高自身数学素质的关键．因此，教师应注重数学思想在日常教学中的渗透，在引导学生探索解题套路、形成解题思路的同时，让学生领悟问题背后的数学思想，促进学生的思维由低阶向高阶发展，从而进一步促进学生的自身发展．

如问题1所示，教师通过层层设问启发学生思考，让学生亲身经历由存疑到解惑的解题过程，进而帮助学生总结其中的数学思想．从整体看，教师通过引导学生将单一的复杂问题逐步转化为多个较为简单的问题，即化未知为已知，化繁难为简单，向学生渗透化归与转化的思想．从局部看，教师为让学生找寻函数恒成立的关键点，通过借助图象来表示代数关系，向学生渗透数形结合的思想；教师应用方程思想，引导学生分析函数求导后的数量关系，让学生求出极值点；对参数a的取值范围的讨论，还渗透了分类讨论思想．可见，教师通过一题即可向学生渗透多种数学思想，从而使学生对问题有更加深入地理解．当然，教师还可从多个类型的题目中，总结提炼出同一数学思想，帮助学生对知识形成更加系统地理解．

总之，数学解题需要套路，但又不能止于套路，教师应在解题套路的探索中，引导学生提炼解题思路，在解题思路的提炼中，引导学生领悟解题思想，从而使学生的数学解题，从浅层走向深层，从自发走向自觉，以此提高数学解题教学的效率和效益．