各向异性地层中的偶极声波测井响应特性及反演

仵 杰，雪宇超，路 涛，李高仁，陈广识

(1.西安石油大学 电子工程学院，陕西 西安 710065； 2.光电油气测井与信息检测教育部重点实验室，陕西 西安710065；3.中国石油集团测井有限公司，陕西 西安 710077； 4.中国石油天然气集团 长庆油田勘探开发研究院，陕西 西安 710018)

引 言

在测井勘探中采集的井孔声波测量值会受到围岩影响，也会受到砂岩层、页岩层引起的各向异性、不平衡地层应力以及裂缝的影响，致使声波测井的解释变得复杂，并使岩层力学特性参数的估算产生偏差[1-2]。其中地层不平衡应力是造成储层油气运移的主要原因，确定地层应力参数及分布能有效预测储层方位[3]。地层油气运移会改变应力方向上地层的声学特性从而引起地层纵波、横波等声学各向异性[4-5]。关于地层纵波各向异性的研究，国内外已做了大量的工作[6-7]。目前,定量分析地层横波各向异性对声波测井阵列波形的影响方面的研究较少。偶极声波测井激发的弯曲波是描述不同方向、不同强度的地层异常应力的关键手段[8]。与均匀地层相比，横波各向异性地层情况下偶极子声源激发的声场更为复杂，无法采用解析的方法进行模拟，一般采用三维有限元方法对不同地层各向异性下的偶极声源激发的反射声场影响因素进行数值模拟[9]。

本文基于COMSOL仿真软件实现了各向异性地层下偶极声波测井阵列波形的数值模拟，研究不同应力方向角及地层横波各向异性强度对阵列波形的影响规律，并通过合适算法反演各向异性地层参数， 以期为横波各向异性地层下偶极声波测井工程应用解释提供理论依据。

1 各向异性地层及偶极声波测井模型的建立

某油田主要产油层段储层非均质性较强，单井产量普遍较低。为改善油气开发效果，需要采用人工压裂等措施。人工压裂会使储层及地层应力方位发生改变，同时可能会影响非均质储层产生地层各向异性，从而影响偶极声波测井数据，无法呈现真实储层信息。若能通过测井响应趋势特征判断偶极声波测井探测储层是否具有各向异性，可以避免不必要的工程损失，提高测井效率。

国内外岩石物理实验证实，当地层存在应力时，沿着应力方向的地层变得更致密，从而声速增大，而垂直方向地层声速则相应减小。为此本文利用COMSOL有限元软件建立图1(a)所示的各向异性地层模型，并进行网格剖分。将实际地层各向异性简化为在相互正交的2个方向上存在声速不同的地层，能够以较为简单的方式反映地层应力产生的各向异性特性。在声场有限元数值模拟中，网格对声场的解析受声场中声波波长控制，可知声波波长由波速与频率共同决定，本文确定声源频率为4 kHz，即模型网格疏密程度受其声速影响。图1(a)中可观察到模型网格由密到疏依次为井孔、低声速地层以及高声速地层，符合剖分规律。

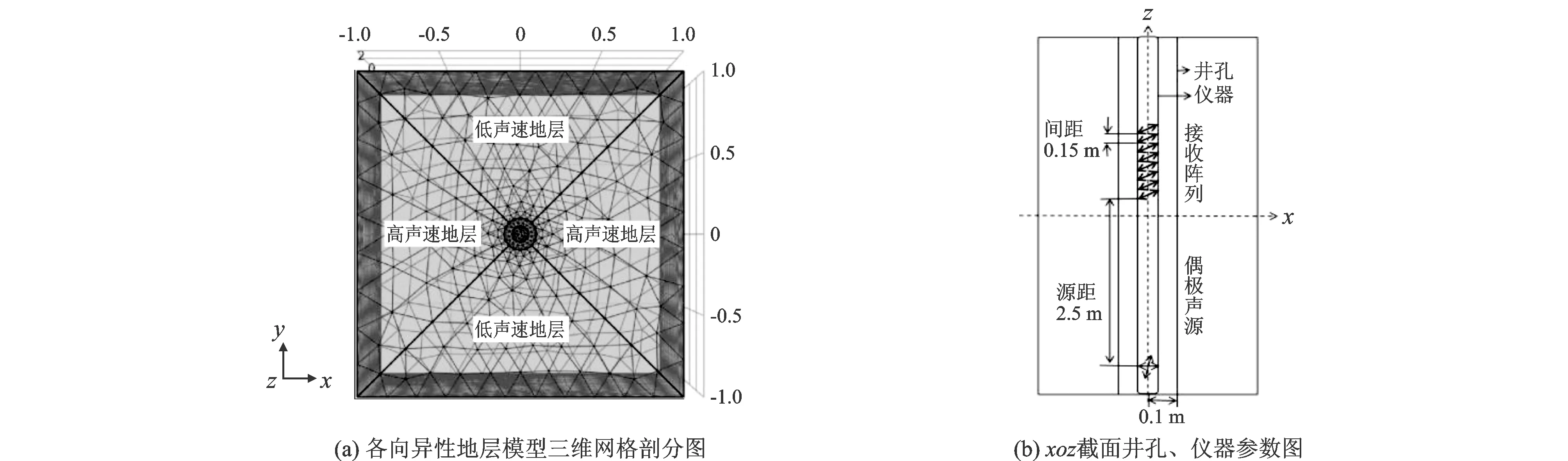
图1 正演模型剖分图及xoz截面示意图

图1(b)给出了xoz截面充液井孔计算模型。模型井眼与仪器同轴，沿垂直井轴方向从里到外的介质依次为仪器、泥浆滤液、地层，仪器源距(偶极声源到第一个接收换能器之间的距离)为2.5 m；仪器间距(z方向上相邻2个接收换能器阵列之间的距离)为0.15 m；井眼直径为标准8 in(1 in=25.4 mm)；数值模拟中不考虑隔声体，用正负偶极子作为横波声源。

为了使激励不易被噪声干扰，选取时域平滑、频谱信号分辨率高的高斯函数为偶极声源函数，在仪器外径处加载2个震动相位相反的点声源模拟偶极子声源，高斯声源函数时域表达式如下：

G(t)=-2π2f02(t-tp)e-π2f02(t-tp)2。

(1)

式中：t为时间；tp为初振相，tp=1/f0；f0为中心频率，4 kHz。

2 横波分裂原理及波形反演方法

2.1 横波分裂原理

偶极子声波测井仪器收集4分量的偶极子声波阵列信号，32个接收换能器对称分布在三维坐标系的X和Y方向。4分量波形数据中，存在2组同向分量(XX和YY)和2组交叉分量(XY和YX)，本文中分量的第一个字母代表发射偶极子的方向，第二个字母代表接收器的方向。

各向异性地层使沿不同方向传播的横波方位及速度产生差异。偶极声源激发的滑行横波穿过井壁进入各向异性地层，由于横波分裂理论，将分为分别沿快慢波面以不同速度传播的正交极化的快主横波(FP)和慢主横波(SP)，在实际地层勘探中，偶极声源偏振方向一般与快慢横波面有一定夹角θ，如图2所示。

图2 横波分裂：发射、接收横波与快慢横波分量关系

2.2 波形反演算法

2.2.1 波形匹配反演算法

本文的各向异性反演方法是以快慢主波波形相似的数值模拟理论为依据，考虑到4分量32个接收换能器接收到的阵列中快慢主波的各种可能组合建立反演目标函数，通过求其全局最优解得到各向异性参数。反演算法采用了快慢波匹配、方位角、各向异性值联合反演的方法，目的是能够较快地得到地层的各向异性参数及方位角。此算法具有高精度、高效率的优势，通过多次迭代抑制和消除波形数据的噪声干扰，最终求取全局最优解。本方法成为现今通过偶极声波测井响应波形信号反演各向异性参数应用最多的方法，其宗旨是通过优化算法最小化目标函数，即

(2)

式中：T积分时窗取整个波形时间跨度；s1和s2分别为声源到接收器阵列跨度内快、慢横波的慢度，慢度差δs=s2-s1；θ为方位角；m和n为决定进行波形相似匹配的任意2个接收器位置；zm是声源到第m个接收器之间的距离；δz是相邻接收换能器之间的距离；N为接收换能器的总数(N=8)；t为积分时间。

针对本文所研究的地层各向异性情况，依托目标函数式(2)所表示的快、慢波形间的数学相似性原理对响应波形进行解析。如图3所示，首先假设快、慢波相似，若慢波在时间上向前移动到快波位置与之匹配，两者应该基本重合。

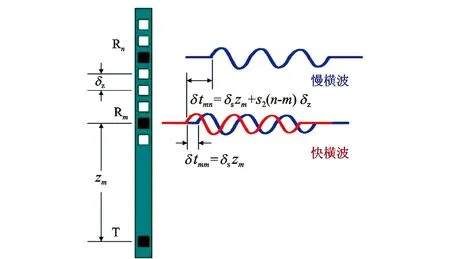
图3 波形匹配示意图

图3所示的是偶极声波测井仪器4个收发声系阵列的其中一个子阵列的排列情况，图中参数分别为：T表示发射声系；Rn、Rm分别为此子阵列接收声系中的任意2个，n、m分别表示第几个接收器；δtmm表示在Rm接收器处快慢横波的到时时差，δtmn表示Rm接收的快横波和Rn接收的慢横波之间的到时时差。

第m个接收器处，波形匹配的表达式为

(3)

将第m个接收器与第n个接收器处波形进行匹配

SPn(t+δtmn)=SPn(t+δszm+s2(n-m)δz)≈

FPm(t)

(4)

通过分析4分量32个接收换能器采集的波形信号，利用算法能够提取出快横波传播方向以及基于偶极声源偏振方向的偏移角θ和快慢横波慢度差，其结果可以表征应力方向以及各向异性强度。

2.2.2 能量各向异性算法

地层能量各向异性是表征地层各向异性强度的参数之一。此算法的内核是直接计算交叉分量相对于4分量波形总能量的能量占比，由于能量各向异性结果受计算误差的影响很小，其结果可靠性高，可以高精度地表征地层各向异性强度，同时可以校正经波形匹配反演算法计算的阵列各向异性结果(即经阵列波形结果进行波形匹配计算的各向异性强度)。

若某方位角θ上接收到4分量偶极波形分别为XX，XY，YX，YY，定义一个波形的能量为波形各个采样点值的绝对值之和

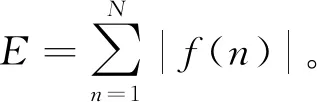
(5)

式中：f为波形函数，N为波形取样点数，E为波形能量。

定义交叉分量与波形总能量的百分比，即交叉分量相对能量为

(6)

定义交叉分量相对能量最大值和最小值，分别为

(7)

定义能量各向异性A为

(8)

3 数值模拟结果及分析

本文数值模拟主要研究基于地应力的地层各向异性对偶极声波测井全波波形的影响。快慢地层分别在应力与垂直于应力的方向。为清晰分析各向异性参数对模型的影响，定义引起地层各向异性方向与偶极声源X偏振方向之间的夹角为θ，定义地层各向异性强度系数

K=vl/vh。

(9)

式中：vh和vl分别为造成地层横波各向异性的快慢横波波速。K值大小与地层各向异性强度呈反比。

3.1 各向异性方向对偶极测井波形影响分析

数值模拟采用的井孔流体和各向异性地层快慢横波声速参数的确定既要符合本文正演研究假设，同时也要结合实际的合理的测井参数。考虑本文研究的井旁各向异性情况，给定井孔内流体和地层快慢声学参数，见表1。

表1 井孔流体及各向异性地层声学参数

拟定采用的地层各向异性强度为K=0.73，各向异性方位角分别为θ=30°和90°。数值模拟结果如图4、图5所示。

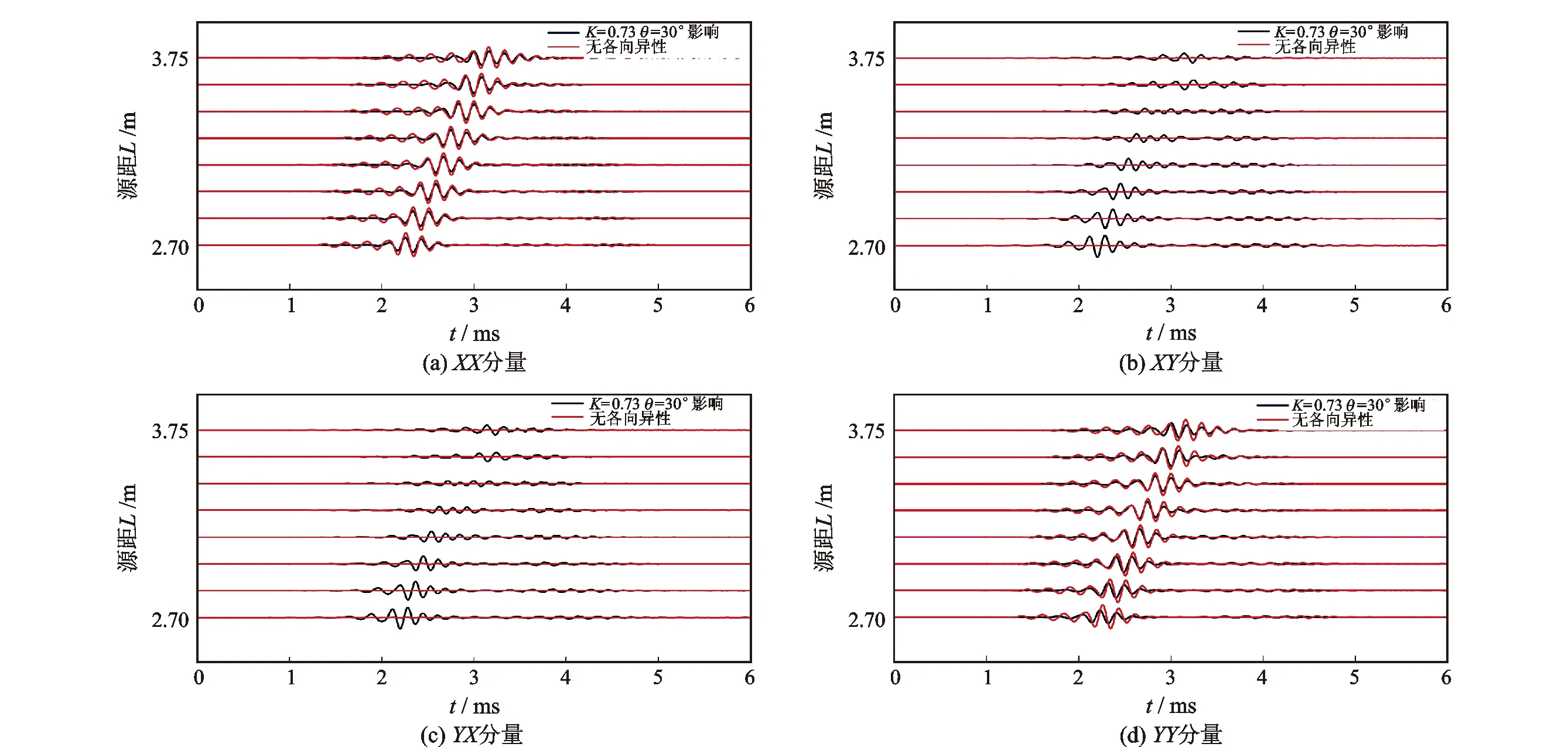
图4 K=0.73，θ=30°各向异性对偶极测井阵列波形的影响

图5 K=0.73，θ=90°各向异性对偶极测井阵列波形的影响

波形幅度分析：

(1)交叉分量：对于各向同性地层，其交叉分量波形信号强度很低；当地层存在各向异性且各向异性强度K=0.73，方位角θ分别为30°时，各向异性地层在介质分界面发生耦合作用，弯曲波发生分裂现象，致使交叉分量能量变高，阵列波形幅度变大。当各向异性方位角θ=90°时，主应力方向与Y发射方向一致，弯曲波分裂程度很低，其交叉分量波形能量与各向同性地层波形振幅在同一数量级。

(2)同向分量：各向异性强度相同条件下，2种不同各向异性方位角对同向分量波形的影响为首波波形振幅均衰减明显，且全波波形相位均向时间零刻度方向发生偏移，但各向异性方位角变化对同相分量阵列波形影响不大。

3.2 基于FFT变换能量谱的研究

FFT是离散傅里叶变换的简称。对声波数据流式信号的分析通常分为2个方面，一方面是其在时间域上连续的波形特征分析，例如振幅以及振型到时和结束等；另一方面是频谱分析，从频域角度解析波形得到更多有用的信息，例如可以得到波形在一个时间区段上的不同频率下的能量分布和幅值分布，进行波形解析后可以得到所研究波形的主要能量及其幅度所在频率范围。对上节不同各向异性方位角下偶极声波测井响应波形进行频谱变换得到频谱图，如图6—图7所示。

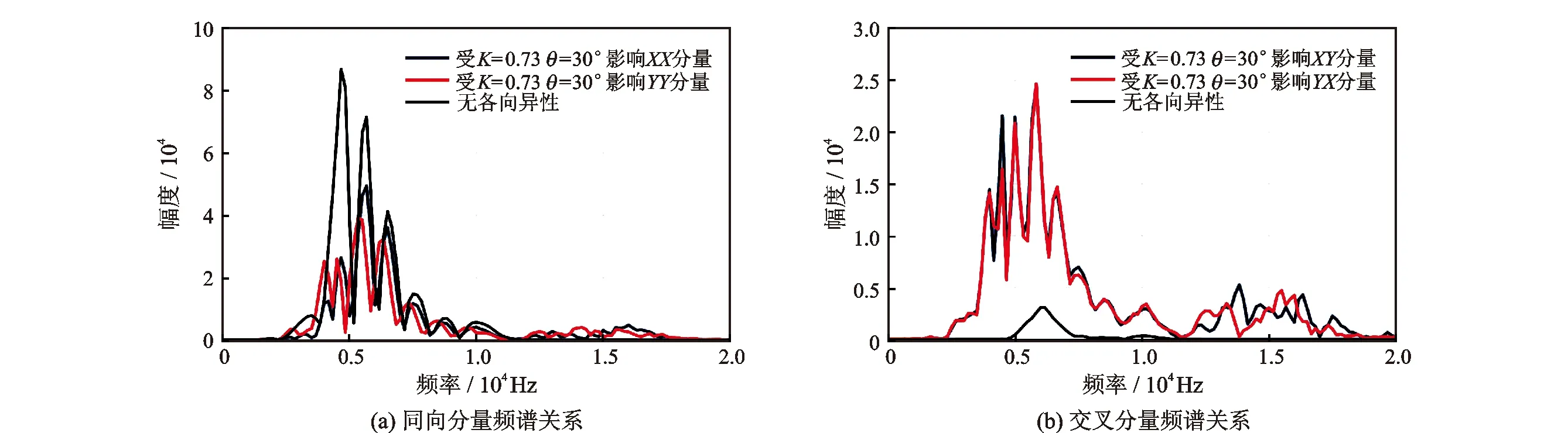
图6 θ=30°时频谱图

图7 θ=90°时频谱图

波形能量频谱分析：

(1)各向异性方位角θ=30°时：由图6(a)(b)可知，同相分量波形能量在声源中心频率处波形幅度衰减最大，同向分量波形能量衰减接近70%，结果与同向分量波形衰减趋势吻合，XX分量波形平均能量衰减接近43%，YY分量波形能量平均衰减近55%，表明各向异性方位角θ=30°造成横波分裂后，XX分量的能量大于YY分量，结论与各向异性地层横波分裂理论相符； 交叉分量波形能量受各向异性影响涨幅较大，波形平均能量增长近5倍。

(2)各向异性方位角θ=90°时：由图7(a)(b)可知，当主应力方向与Y发射方向同向，横向各向异性产生的快慢波面分别坐落于仪器的Y和X接收方向，此时横向各向异性造成横波分裂程度最低，同向分量波形能量衰减减少，XX分量平均能量衰减近41%，YY分量平均能量衰减近33%；交叉分量平均能量与各向同性地层中测得的波形的能量相近。

3.3 各向异性强度对偶极声波测井影响分析

各向异性地层所表示出声学特性的差异决定了各向异性强度。本节模拟分析3种各向异性方向情况下不同各向异性强度对偶极声波测井全波波形的影响。计算得到的波形如图8—图9所示。

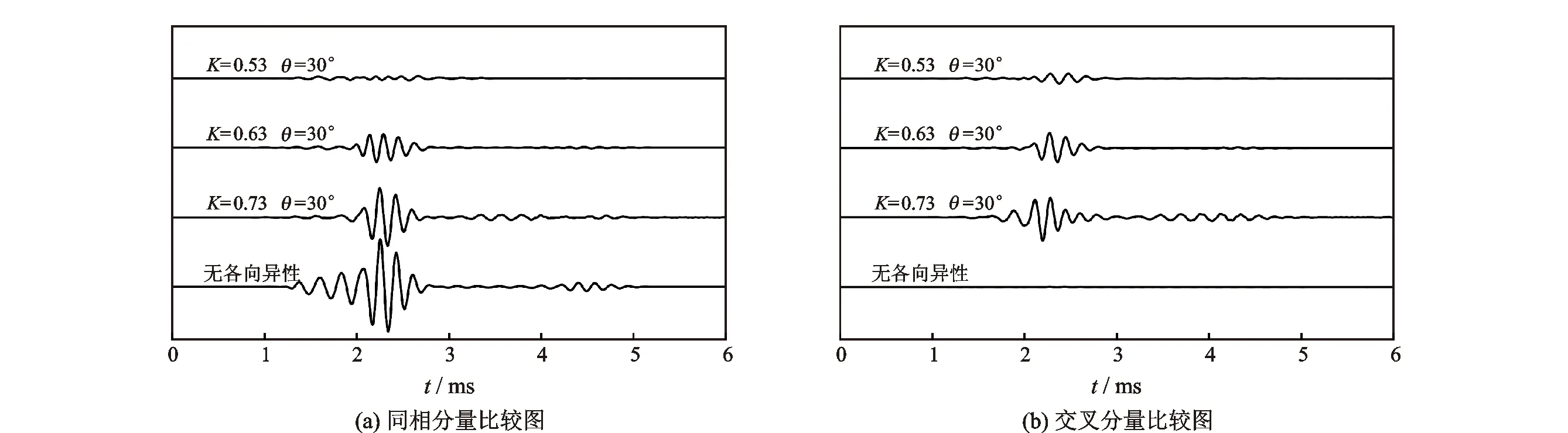
图8 θ=30°时3种各向异性强度对波形影响趋势

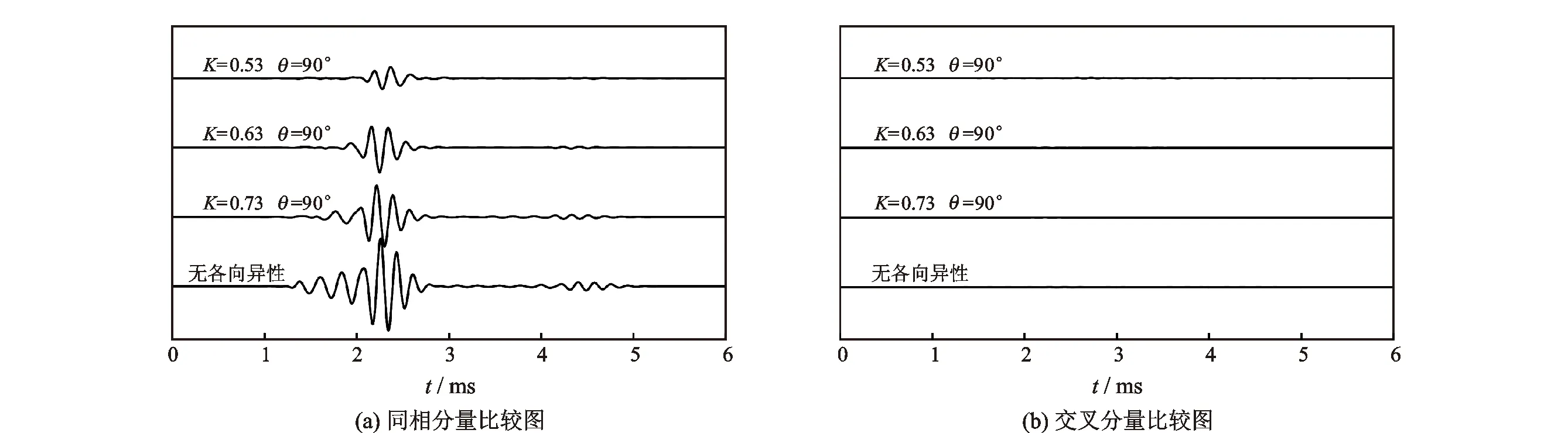
图9 θ=90°时3种各向异性强度对波形影响趋势

波形分析如下：

(1)同向分量：由图8(a)、图9(a)可知，各向异性地层对波形幅度影响显著，同向分量波形幅度明显减小，波形幅度减少程度随着各向异性强度系数K的变小而变大。

(2)交叉分量：交叉分量是各向异性地层不同横波波速地层分界面耦合的产物，通常分界面两边地层声学性质差异越大，其波形能量越强，如图8(b)所示。机理在于本文正演模型地层的特殊性，地层各向异性分界面始终处于交叉分量声波从发射到接收的途径中，声波通过2种不同声学特性介质分界面时发生反射与折射，导致交叉分量波形能量发生衰减，且声波衰减程度随分界面两边地层横波波速差异变大而变强。图9(b)中，3种横波各向异性强度造成交叉分量波形幅度很小且不随系数K变化，结果产生了逆常理性现象，原因在于此时快慢波面分别坐落于偶极声源偏振方向，造成弯曲波分裂程度很低，致使交叉分量波形振幅极低。而无各向异性的均匀地层则几乎不存在交叉分量信息，如图8(b)，图9(b)交叉分量第一道波形所示。

4 反演分析

本文将有限元数值模拟正演得到的4分量阵列波形响应数据作为式(2)的输入，以各向异性地层中横波分裂为具有相似特征的快、慢横波为理论基础，使用模拟退火算法得到目标函数在求解域中的全局最小值，反演出地层各向异性参数包括慢横波的慢度s2、快慢横波之间的差异δs以及最大应力方位角θ，此时快横波慢度s1=s2-δs。根据本文各向异性模型的正演计算阵列波形进行参数反演，反演目的是为了验证正演结果的正确性。 为了便于比较分析反演效果，选取预设模型参数，见表2。

表2 参与反演过程的正演横波各向异性参数

将各向异性方位角θ=30°、90°对应的正演阵列波形结果作为反演对象，设置内部迭代次数N=100进行迭代计算。由于模拟退火算法每次迭代在全局中搜寻最小值，其目标函数一般呈波动式逐步减小，缺点为收敛速度较慢；若给定合理反演参数范围，可以加速反演收敛速度，同时得到正确反演结果。本次给定反演角度范围为0～90°，得到反演结果见表3、表4。

表3 模型主应力方向角θ=30°时反演结果对比

表4 模型主应力方向角θ=90°时反演结果对比

反演结果分析如下：

(1)模拟退火优化算法实现了偶极声波测井模型各向异性参数的高精度反演，得到了与预设模型各向异性参数吻合的结果。

(2)各向异性参数变化的同时，对同一种各向异性方位角进行多次反演，其结果与正演参数基本一致，经计算反演相对误差小于5%，在数值计算误差允许范围内。

本文各向异性地层模型描述的地层状态较为复杂，造成地层不同深度处的各向异性描述困难，通过波形匹配反演算法输出快慢横波慢度s1和s2，已知接收器阵列各向异性强度计算公式为2(s2-s1)/(s1+s2)，计算主应力方向角θ=30°、90°下2种工况下的阵列各向异性与能量各向异性，对比结果见表5。

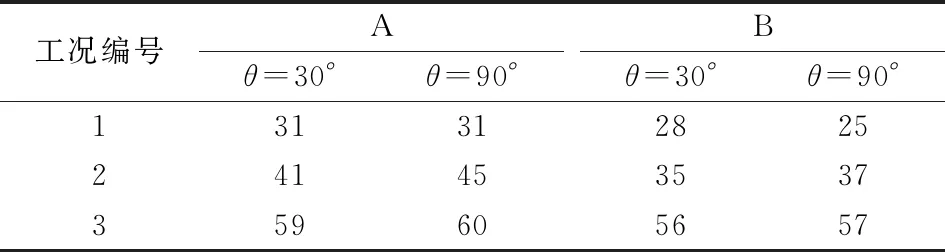
表5 阵列各向异性与能量各向异性对比

由波形匹配算法思想可知，阵列各向异性的结果由算法多次迭代产生，算法迭代存在误差的累积，其结果可能会发生偏差；而能量各向异性表征地层各向异性强度，因能量各向异性算法简洁高效，故结果可靠性更高。将3种各向异性结果进行对比，阵列各向异性结果略大于能量各向异性结果，数值上的差异可能是由于误差迭代产生的，其结果可以正确表征地层的各向异性强度。

5 结论及讨论

(1)地层各向异性方向角对偶极测井波形具有影响，地层各向异性使同相分量波形幅度及能量降低，各向异性方向角的改变对同相分量波形影响不显著；地层出现一定角度异常应力会使交叉分量波形振幅和能量产生明显增长，特殊情况下譬如各向异性方向与声源偏振方向一致，交叉分量波形振幅及能量达到最小。

(2)地层各向异性强度对偶极测井波形影响较大，同向分量波形振幅的变化程度随地层各向异性强度系数变大而显著减小；根据声波在介质分界面的反射定律和折射定律解释了交叉分量波形产生的逆常理性趋势。

(3)精确反演地层各向异性参数验证了正演模拟的正确性；相较于传统的阵列各向异性反演方法，能量各向异性反演方法能够更准确地反映储层各向异性强度。