基于改进NSGA-Ⅲ的多目标柔性车间调度研究*

孙 浩，刘环宇，赵柏栋，张玉嘉，杨 振，王德权

(大连工业大学机械工程与自动化学院，大连 116034)

0 引言

柔性生产调度问题(flexible job shop scheduling problem,FJSP)是复杂的NP-hard问题[1]，打破了传统刚性大批量生产对设备唯一性的约束，使车间调度变得更加复杂多变。从调度目标数量可将柔性作业车间调度分为：单目标和多目标调度。

相比于单目标调度问题[2-3]，多目标柔性作业车间调度问题更为复杂。首先，难以保证在调度过程中多个目标的优化平衡。其次，多个目标的参数和量纲存在差异。现阶段多目标调度的研究思路分为两种，其一，通过权重将多目标转化为单目标[4-5]；其二，非劣解生成法，利用帕累托原理生成最优解集[6-8]，此方法广泛应用于求解三目标及以上问题。在算法设计上需要对原始算法进行改进或者结合两种不同算法的优点，使算法能够发挥更好的寻优效果。DEB等[9]在NSGA基础上提出了NSGA-Ⅱ算法，提高算法搜索效果和计算效率。CHEN等[10]提出混合算法MGSA- NSGA-Ⅲ，采取混沌变异策略，提高解空间分布的均匀性。LI等[11]在传统NSGA-Ⅲ基础上改进了参考点生成策略和算子选择机制，提高了算法计算效率。求解高维多目标问题时，常见的全局智能算法均存在着种群多样性低、搜索效率差、容易陷入局部最优等缺陷。

综上所述，文章提出了一种改进NSGA-Ⅲ算法，采取4种不同编码方式共同生成初始化种群，并引入邻域搜索策略，解决单一算法种群多样性低、容易陷入局部最优等问题。

1 多目标柔性作业车间调度模型建立

柔性作业车间的柔性表现在加工顺序和设备选择上的不确定性，使多目标调度问题更为复杂。假设，车间共有m台设备和n个待加工工件，并且每个工件含有多道加工工序。工件必须按照工序的加工顺序依次加工，工件的每道工序的加工设备选取须在指定的设备集中，可选设备集中的机器加工能力存在差异。因此，柔性车间调度的两个主要任务：①确定工件的加工顺序；②确定每道工序选择的设备。参数符号含义如表1所示。

表1 参数符号含义

机器集合M={M1,M2,…,Mm}，共有m台设备；工件集合P={P1,P2,…,Pn}，共有n个工件；工序集合J={J1,J2,…,Jn}，Ji={Ji1,Ji2,…,Jik}，Ji表示第i个工件加工的工序数。

(1)目标函数。

①最大完工时间最小；

CM=min(max1≤i≤n(Ci))

(1)

②总设备负荷最小；

(2)

③车间总能耗最小；

(3)

(2)约束条件。

柔性作业车间调度问题可描述成，n个工件在m台设备上加工，且一个工件包含多道工序，每道工序可在一台或多台设备上加工，加工设备选择不同，加工时间及加工功率不同。

①所有设备初始化均为待加工状态。

(4)

②一个工件某一时刻只能加工一道工序。

(5)

式中，k′、k表示对应加工设备编号

③一个工件的某一时刻只能在一台设备上进行加工。

Li,j,t1≠Li,j,t2→t1≠t2

(6)

式中，Li,j,t1为t1时刻执行Oi,j的设备编号；Li,j,t2为t2时刻执行Oi,j的设备编号。

④任意工件只要选定设备开始加工，则过程中不能中断。

(7)

⑤每个工件的每道工序需在特定的设备集中选取。

mi,j∈Mi,j

(8)

2 改进NSGA-Ⅲ算法设计

遗传算法在求解调度优化问题时具备鲁棒性强特点。求解多目标问题时，NSGA-Ⅱ[12]和NSGA-Ⅲ被广泛使用，为了进一步提高算法的效率，避免陷入局部最优，对NSGA-Ⅲ算法做出如下改进。算法流程如图1所示。

图1 改进NSGA-Ⅲ算法流程图

基本步骤如下：

(1)种群初始化阶段，为保证种群分布均匀并且缩小搜索的解空间大小。采取4种不同编码的种群初始化方式；

(2)混合NSGA-Ⅱ基于拥挤度选择和锦标赛的方式，对初始化种群进行筛选，使具有良好基因的个体参与到进化当中；

(3)利用NSGA-Ⅲ的全局搜索能力，对种群进行搜索，选择出下一代优良个体；

(4)结合基于部分解的随机邻域搜索策略，对(3)选择出的优良个体进行邻域搜索，避免丢失更优的个体；

(5)判断算法是否终止，即算法是否迭代到指定代数，是则算法终止，否则继续迭代。

2.1 染色体编码设计

工件的加工工序顺序和每道工序的设备分配是柔性作业车间调度中最基本的两个方面。因此，在此类问题上采取两部分编码方式。第一部分基于工序编码，选取工件编号作为工序部分基因，第二部分基于设备编码，选取设备集中的设备顺序号作为基因。图2以3个工件在3台设备上加工为例来编码。

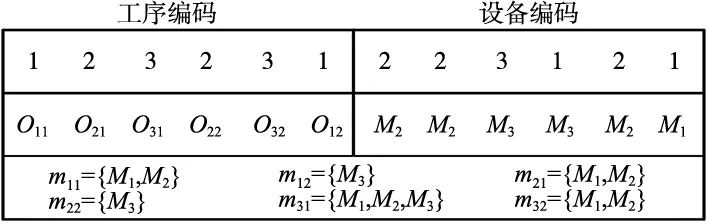
图2 染色体编码

工序编码表示为三个工件的加工顺序，第一个1出现表示O1,1工序，第二个1出现表示O1,2工序。设备编码表示完成某工序可用设备集中所选择设备的顺序号，例如，设备编码中第一个2表示为完成O1,1工序，在m1,1中选择第2个设备M2。

2.2 种群初始化设计

种群空间的均匀性是影响算法性能好坏的重要指标。越是均匀的种群空间，算法的搜索结果往往更优，不容易陷入局部最优等问题。因此，为使种群空间具有均匀性，采用4种不同的编码方式共同生成初始化种群。

(1)采取最长路径(即加工工序最多)加工时间最短原则编码。

(2)采取随机加工工序的加工时间最短原则编码。

(3)采取最长路径加工功率最小原则编码。

(4)采取随机加工工序的加工功率最小原则编码。

2.3 初始化种群个体的选择

锦标赛选择的方式是常见的选择手段之一，而在解决高维多目标问题时，单一的选择方式很难达到理想效果，需要更多的指标来保证选取的合理性。综合考虑算法的计算效率和选取结果的最优程度，提出结合NSGA-Ⅱ中的快速非支配等级和基于拥挤度的选择方式。

(1)计算种群个体的非支配等级和拥挤度大小。

(2)设置锦标赛参赛数量，选择出参赛的个体，再依据非支配排序等级，选出等级较高的个体。

(3)当选择的个体非支配排序等级一致时，选择拥挤度较大的个体。

2.4 交叉与变异

(1)交叉操作。采用模拟二进制交叉方式，分别对工序和设备进行交叉。工序交叉如图3所示，设备交叉如图4所示。

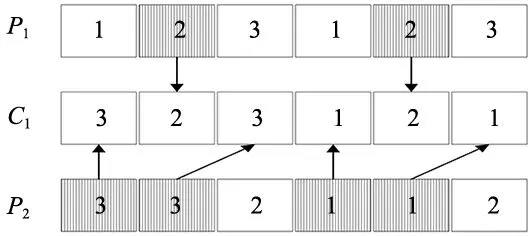
图3 工序交叉示意图

将P1中工序2位置保留，再将P2中不属于工序2 的位置顺序插入到P1中得到子代个体C1,同理，得到C2。

图4 设备交叉示意图

确定父代个体中设备交叉位置，进行交叉生成子代个体。再依据工序染色体对交叉后的设备染色体产生的非法基因按照设备加工时间最短原则进行修正。

(2)变异操作。变异操作采取基于工序交叉和设备交叉的变异方式，利用随机函数产生工序交叉位置，同时保证位置上点数值不同。交叉完成后，工序基因对应的不合理设备基因，按照工序加工时间最短原则进行修正，设备交叉与工序交叉同理。工序交叉变异过程如图5所示。

图5 基于工序交叉的变异图

2.5 基于部分解的随机邻域搜索策略

NSGA-Ⅲ具有良好的全局搜索能力，但其对局部的搜索能力较差，因此算法在迭代过程中往往会出现局部最优的问题。基于此，采取邻域搜索机制[13]与NSGA-Ⅲ算法混合的方式。

(1)首先，设置大小为K的邻域搜索空间。

(2)选择邻域搜索个体，并在该个体中随机选择两个工件的工序作为关键工序，对工件1中所有工序的设备进行重新选择：①当最短加工时间设备唯一，选择该设备加工。②当最短加工时间设备不唯一，选择所有设备中加工功率最小的设备。对工件2中所有工序的设备重新随机选择。

(3)满足初始设定的K值时，结束邻域搜索。

3 仿真验证

首先，验证改进算法目标迭代的收敛情况，再将所提出的改进NSGA-Ⅲ算法与原始NSGA-Ⅲ 算法进行对比验证，观察两个算法在相同实例下所得到的初始解空间的均匀性、大小和非支配解的数量。

算法基本参数如表2所示。

表2 算法基本参数

(1)初始化种群分布和最优解的分布对比。对比NSGA-Ⅲ算法与所提出的改进NSGA-Ⅲ算法在求解MK01算例时初始化种群的分布情况和最优解分布情况，如图6～图8所示。

图6 NSGA-Ⅲ初始 化种群分布图7 改进NSGA-Ⅲ 初始化种群分布

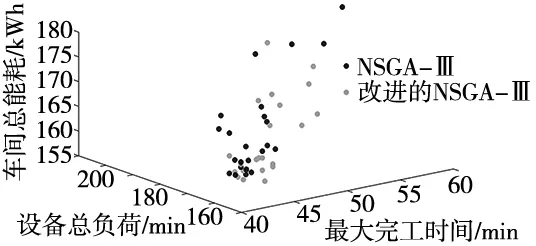
图8 两种算法最优解的分布图

由上述分布图可知，改进NSGA-Ⅲ算法的初始化种群分布更均匀，搜索的解空间更小，且搜索到的最优解收敛更好，求解结果更优。

(2)非支配解对比验证。对于非支配解的验证，采用10个BRdate[14]实例进行仿真。两种算法在10个BRdate实例上搜索到非支配解情况汇总如下：其中NSD表示两个算法搜索到的非支配解总数；～表示没有搜到非支配解；n1|n2中n1代表对应算法搜索到的非支配解数量，n2代表两个算法搜索的非支配解总数。具体非支配解信息汇总如表3所示。

表3 两种算法的非支配解

由上表可知，改进NSGA-Ⅲ在10组BRdate算例中搜索到非支配解数占76%，而NSGA-Ⅲ搜索到非支配解数占24%，改进NSGA-Ⅲ有效性得以验证。

4 总结

针对柔性作业车间调度问题，建立以最小化完工时间，设备总负荷和车间总能耗为目标的多目标调度模型，并对求解多目标问题具有良好鲁棒性的NSGA-Ⅲ算法做出改进。首先，采取4种不同编码方式的种群初始化策略，使得种群分布均匀的同时，缩小搜索的解空间大小。在进化阶段，混合了NSGA-Ⅱ基于拥挤度的父代种群选择和基于部分解的邻域搜索策略，防止算法在实现全局搜索时，陷入局部最优。

最终，通过10个BRdate标准算例对所提出的改进NSGA-Ⅲ算法与原始NSGA-Ⅲ算法进行对比验证。依据初始化种群的均匀性、搜索解空间的大小和非支配解的数量等指标来判断算法的优劣，证明所提出算法的有效性。