基于粒子群模糊神经网络的立方体机器人建模*
2022-07-27黄卫华何佳乐
陈 阳,黄卫华,何佳乐,章 政
(武汉科技大学信息科学与工程学院,武汉 430081)
0 引言
立方体机器人是一种具有全封闭或半封闭外壳的新型机器人[1],它通过安装在立方体内部某个面的动量轮的旋转产生重心偏移,基于动量守恒等原理实现立方体机器人以单点或者棱边为支点的自平衡与翻滚等运动。与传统的轮式、腿式、履带式等移动机器人相比,立方体机器人具有独特的机械结构和运动方式,是一种控制理论研究与应用的理想平台,在太空探索、编队表演、桥梁修补等领域具有广泛的应用前景。
目前,立方体机器人的结构设计大同小异[2-4],相关研究工作主要集中于立方体机器人的动力学建模与控制系统设计。关于立方体机器人动力学建模的研究一般是基于凯恩方程[5-6]或拉格朗日方程[7]建立立方体机器人的驱动力矩与速度、角速度等运动量之间的关系。然后对所建立的立方体机器人动力学模型,采用自抗扰控制[7]、PID控制[8]、模糊控制[9]及反馈线性化[10]等方法实现立方体机器人的自平衡稳定控制。然而,立方体机器人是一种非线性、强耦合、欠驱动及多变量的多自由度倒立摆系统,复杂的结构和特殊自平衡方式导致其机理模型存在动态不确定性。
已有研究表明,模糊神经网络已被广泛应用于处理非线性、模糊性等问题[11]。目前对于立方体机器人建模的研究均采用机理建模方法,因此难以获取立方体机器人精确的数学模型,从而影响了立方体机器人控制系统的性能。为了进一步提高立方体机器人建模精度,提出一种基于粒子群算法优化的T-S型模糊神经网络,通过模糊神经网络的训练学习,粒子群算法优化模型参数,建立立方体机器人的动力学模型。最后仿真与实测实验结果证明了所设计的基于粒子群模糊神经网络模型的可行性和有效性。
1 立方体机器人结构设计
棱边自平衡的立方体机器人机械结构如图1所示。外框由2个0.144×0.144 m2、2个0.142×0.144 m2和2个0.144×0.144 m2的环氧树脂材料组装而成;惯性轮独立安装在立方体的一面上,内部集成了姿态传感器模块、主控模块、电源模块和电机驱动模块;电机自带AB相编码器,可以有效避免安装外部编码器造成不对称问题。

1.自平衡立方体框架 2.主控板 3.永磁直流电机4.12 V锂电池 5.电机固定件 6.法兰联轴器 7.惯性轮
立方体机器人的主要参数以及数据如表1所示。

表1 立方体机器人的主要参数表
2 动力学建模及分析
立方体机器人系统为可等效为一个典型的多变量、高阶、非线性、不稳定的多自由度空间动量轮倒立摆系统。建立如图2所示系统坐标系。

图2 自平衡立方体机器人坐标系定义
图中,机体坐标系为O-XYZ,Y轴为立方体机器人以棱边为支点的所在边,坐标原点O为动量轮所在面与Y轴相交处。立方体机器人的重心为G,立方体与地面接触点等效为坐标系原点进行转动;惯性轮转过的角度为θ,惯性轮绕重心G;立方体相对于纵轴的偏转角为α。
为了方便在数学上推导和处理问题,作出如下假设:①立方体框架在运动中是不变形的刚体;②忽略空气阻力。
立方体机器人系统的拉格朗日方程为:
(1)
式中,L为拉格朗日算子;q为系统的广义坐标;T为系统的总动能;V为系统的总势能。
由此可得,立方体机器人的拉格朗日算子为:
(2)
立方体机器人系统的广义力矩为:
(3)
式中,U为惯性轮的驱动力矩。将式(2)、式(3)带入拉格朗日方程中,则有:
(4)
由此可得,立方体机器人系统的动力学方程为:
(5)
由此可得立方体机器人在俯仰方向上的动力学模型的状态方程为:
(6)

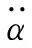
3 基于模糊神经网络的立方体机器人建模
3.1 T-S型模糊神经网络结构设计


图3 立方体机器人的模糊神经网络
立方体机器人的模糊神经网络结构描述如下:


(7)
式中,Ai、Bi、Ci为模糊子集;(Pj,Qj)是第j个立方体子系统相应维数矩阵;xj为系统的第j个状态变量。
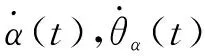
(8)
式中,cij和σij分别是高斯隶属度函数的中心和宽度;μAi就是Ai的隶属函数值,表示α(t)属于Ai的程度。
第2层计算每条规则的隶属度:
ωj=μAi*μBi*μCi
(9)
第3层输出为每条模糊规则推理所占的权重。其中第j个节点计算第j条规则的归一化:
(10)
第4层计算模糊规则的输出结果,其中每个节点都是一个自适应节点。第j个节点具有输出:
(11)
第5层输出所有输入信号之和,也就是模糊推理的结果:
M=∑iZjj=1,2,...,27
(12)
3.2 基于粒子群的模糊神经网络参数辨识
对于所建立的立方体机器人模糊神经网络的学习过程而言,主要是第二层的各模糊子集的隶属函数中心、宽度和后件网络连接权值的更新过程。通常采用误差反向传播算法实现模糊神经网络的参数辨识[12],易导致收敛速度会减慢以及陷入参数局部优化,从而影响了模糊神经网络的泛化能力。粒子群算法(particle swarm optimization,PS0)是一种通过模拟鸟群捕食行为来进行群体迭代的全局随机搜索算法,具有收敛速度快、易于实现、易于理解并且仅有少量参数需要调整等优点[13]。针对此种问题,采用粒子群算法优化模糊神经网络中的参数。
设机器人模糊神经网络的粒子群由N维向量组成,用种群中微粒的坐标矢量F表示模糊神经网络模型的高斯隶属度的中心cij,宽度σij和后件网络的连接权值。以每个粒子对应的网络参数在训练集上产生的均方差作为粒子的适应度的目标函数,适应度越小,E就越小,网络对数据的拟合程度就越高。模糊神经网络的性能指标为:
(13)
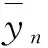
粒子群体的最佳位置对应的便是立方体机器人模糊神经网络中各规则层节点最优的隶属度函数的中心值,宽度以及后件网络的连接权值。粒子群算法中粒子速度和位置按式(14)进行更新:
(14)

3.3 粒子群模糊神经网络模型实现步骤
基于粒子群的模糊神经网络的算法步骤如下:
步骤1:首先初始化粒子群的起始参数,粒子维度d等于立方体模糊神经网络中所有需要训练的参数数量,惯性权重λ,设其最大值为1,最小值为0,最大速度设为1,学习因子c1c2均设为2。然后再依据输入数据集的特征搭建模糊神经网络模型,初始化模糊神经网络初始参数,利用模糊聚类方法获得最优的隐层节点数目 ,并选择合适的样本输入作为初始的数据中心cij,取聚类半径为初始宽度σij;
步骤2:使学习训练样本经过模糊神经网络计算每条规则的适用度和每条模糊规则推理所占的权重。再计算模糊规则的输出结果,其中每个节点都是一个自适应节点。最后输出所有输入信号之和,也就是模糊推理的结果。以模糊神经网络模型的均方差表示粒子群算法的适应度函数值,当适应度函数值在给定范围之内,就停止计算,此时模糊神经网络可得最优;
步骤3:更新粒子位置和速度。随机生成n个粒子个体,每个个体均由群体的位置矩阵和对应粒子的速度矩阵两部分组成,假设pbnd为第n个个体的最佳位置,那么初始化时便将第n个个体的当前位置定义为该个体的最佳位置pbnd;
步骤4:确定适应度函数,计算每个粒子的适应度值。选择均方误差最小作为粒子群算法的寻优目标,因此将式(14)设置为粒子群算法的适应度函数,并由此计算出每个粒子的适应度,并对其进行评价;
步骤5:判读是否满足终止条件,如果达到最大迭代次数或者适应度达到预设精度,则停止寻优迭代;否则返回步骤3,直到达到要求为止;
步骤6:迭代停止后,种群所经历的最佳位置pbnd的值就是全局最优解,将其值赋予立方体模糊神经网络隶属函数的中心和宽度以及连接权值。将更新后的最优参数传回到步骤2中,得到最优的模糊神经网络模型。
4 仿真与实测实验
4.1 仿真实验及结果分析
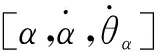
分别采用T-S型模糊神经网络与基于粒子群优化的T-S型模糊神经网络对立方体机器人系统的输入、输出数据进行训练,系统的均方误差曲线如图4所示。通过表2可以看出粒子群模糊神经网络相较于模糊神经网络均方误差值小,训练时间短,迭代次数少。
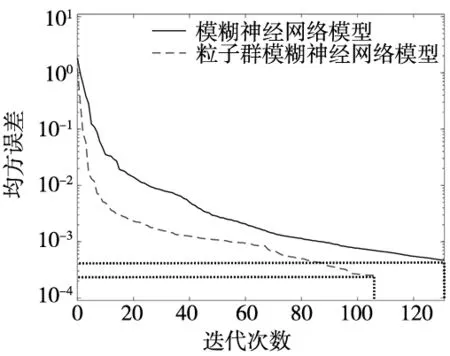
图4 立方体机器人模糊神经网络均方误差仿真图

表2 模糊神经网络与粒子群模糊神经网络对比
取测试样本中的200组数据用以测试粒子群模糊神经网络模型与立方体机理模型的预测输出,如图5~图7所示,对比两条曲线可以得出粒子群模糊神经网络模型预测输出相较于机理模型预测输出的立方体角度值,立方体角速度值和惯性轮的角速度值数据输出误差小,精度高。图8~图10分别为粒子群模糊神经网络模型与机理模型的机体角度、机体角速度和惯性轮角速度的误差输出值,可以明显看出粒子群模糊神经网络模型的输出误差均小于机理模型的输出误差。

图5 立方体角度值输出对比图6 立方体角速度值输出对比

图7 惯性轮角速度值输出对比图8 立方体角度输出误差值
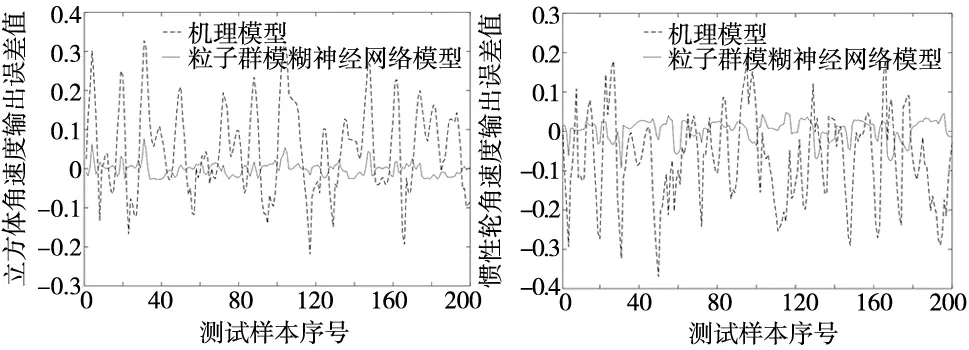
图9 立方体角速度输出误差值图10 惯性轮角速度输出误差值
对比结果如表3所示,立方体机器人粒子群模糊神经网络模型的机体角度输出误差、机体角速度输出误差和惯性轮角速度输出误差均小于立方体机理模型的输出误差。由此可见,粒子群模糊神经网络模型所得到的输出数据相较于常规机理模型的精度更高。

表3 粒子群模糊神经网络模型与机理模型对比
4.2 实测实验及结果分析
为了验证所设计建模方法的实用性,将粒子群模糊神经网络模型和机理模型应用到立方体机器人实物中对比,选用PID控制器进行稳定性控制,得到如图11所示的实物运行状态。

图11 实物运行图
当立方体机器人处于稳定状态,在T=0 s时采用两种不同模型的立方体机器人同时工作在稳定状态;T=3 s时,给立方体机器人一个相同的风力干扰;T=4 s时,立方体机器人同时进行稳态调整;T=5 s时,粒子群模糊神经网络模型的立方体机器人达到稳定状态;T=7 s时,采用机理模型的立方体机器人达到稳定状态。由表4可知,在相同大小的扰动下,采用粒子群模糊神经网络模型的立方体机器人相较于机理模型的立方体机器人摆动角度更小,回到稳定状态更快。实验证明了基于粒子群模糊神经网络模型的立方体机器人相较于机理模型的立方体机器人抗扰性更好,回到稳态的时间更短,控制精度更高。

表4 粒子群模糊神经网络模型与机理模型实物运行对比
5 结论
以立方体棱边为支点的立方体机器人,针对其具有非线性、欠驱动、强耦合、多变量等复杂特性,设计并实现了一种基于粒子群模糊神经网络模型的立方体机器人系统。通过对立方体机器人机体的输入输出数据进行学习,由此建立立方体机器人的粒子群模糊神经网络模型。引入粒子群优化模糊神经网络参数,增强了立方体机器人模型的泛化能力、提高网络的收敛速度并避免出现局部优化的问题;使误差收敛到设定值的速度更快。最后仿真与实物实验结果表明:针对立方体机器人具有非线性、欠驱动、强耦合、多变量等复杂特性所设计的粒子群模糊神经网络模型,相较于基于机理模型的立方体机器人系统具有良好的稳定性、抗干扰能力。
