线激光传感器测量系统的安装姿态标定方法*

叶柳康，叶文华，杨高杰，肖 晓

(1.南京航空航天大学机电学院，南京 210016；2.航空工业济南特种结构研究所，济南 250023)

0 引言

激光三角测量技术因精度高、效率高、测量无损伤等优点，被广泛用于加工检测中[1-3]。相对于点激光，线激光测量效率更高，应用更广。

线激光传感器只含X、Z轴数据，无法完成零件特征检测，一般与运动机构组成系统实现三维测量[4-5]，系统测量精度受运动机构精度、传感器分辨率、安装姿态、测量环境等影响，其中安装姿态可在传感器安装完成后对其标定，以此提高系统精度。国内外对激光传感器系统标定问题展开了许多研究，主要研究方向是机器人测量系统的手眼标定[6-9]，常用方法为定点变位姿法。黄佳等[10]令机器人变位姿测量固定球心，由球心位置不变原则解算机器人与传感器位姿关系。吴聊等[11]以平面为靶标，以平面在机器人不同位姿下的测点求解标定参数。定点变位姿法虽然方法简单，但对几何误差敏感[12]，另外，载体为移动机构的测量系统姿态无法任意变化，以该方法标定误差较大。机床测量系统中，徐舒婷[13]提出了一种方向标定方法，以阶梯面标定三个方向偏角并进行角度校正，方法简单，但需要额外的调整机构，且对阶梯面精度要求高。相对其他特征，球面具有各向同性且定位准确的特点，但受传感器测量特性影响[14]，线激光测量球面的Z向误差较大，直接以球面标定会影响精度。虽然平面定位效果与标定精度均不如球面[15]，但平面比球面的线激光测量Z向误差小。

为了实现准确标定，本文提出一种线激光传感器测量系统的安装姿态标定方法。建立了测量系统标定模型，并以欧拉角描述安装姿态，以平面和球面为靶标分析绕X、Y、Z轴转动的姿态角，最后解算姿态矩阵。该方法结合了平面与球面的线激光测量特性，减小测量误差对标定的影响，可有效提高标定精度。

1 线激光传感器测量系统建模

系统由X、Y、Z三轴移动机构，线激光传感器，数据传输线和上位机等组成，其中线激光传感器采用了激光三角测量技术。在移动机构末端安装线激光传感器，使其按指定路径对零件扫描，传感器数据与机构数据以数据线传输到上位机构成三维数据，经过数据分析得到测量结果。实现精密测量的关键在于传感器X、Z轴数据与机构数据的融合，传感器姿态是影响最大的因素之一，因此测量系统的安装姿态标定十分必要。

图1 测量系统介绍

为了描述坐标系之间的关系，定义ObXbYbZb表示测量系统的基坐标系，OLXLYLZL表示末端坐标系，OsXsYsZs表示传感器坐标系。由于载体是移动机构，可定义末端坐标系与基坐标系的坐标轴同向，传感器坐标系与基坐标系的关系由安装姿态决定，如图1所示。

根据运动学关系，被测点应满足坐标转换关系：

xb=RL(Rsxs+Ts)+TL

(1)

式中，xb、xs分别为被测点在基坐标系、传感器坐标系下的坐标；RL、TL为末端坐标系相对基坐标系的变换矩阵；Rs、Ts为传感器坐标系相对末端坐标系的变换矩阵。由坐标系定义知RL=I3×3，可将式(1)简化为：

xb=Rsxs+Ts+TL

(2)

平移矩阵Ts与传感器安装位置、末端坐标系定义有关。为了简化过程，定义此次安装标定的末端坐标系原点OL与传感器坐标系原点Os重合，即Ts=(0,0,0)T，并设一固定参考点。若需重新安装标定时，以参考点为基准校正Ts即可。平移矩阵TL由移动机构的运动学关系得到，因此只需求解线激光传感器姿态即可得到旋转矩阵Rs完成标定。

2 测量系统标定方法

2.1 定点变位姿法

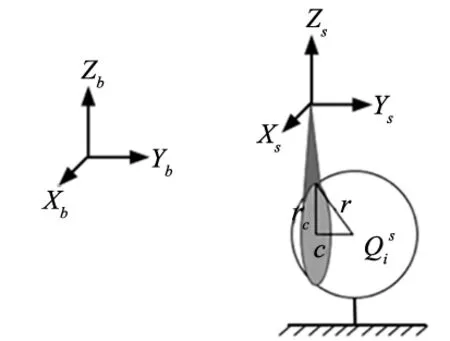
图2 定点变位姿法原理

设机器人基坐标系下的球心坐标为Qi(i=1,2,…,q)，由基坐标系下球心位置不变原则，得到以下关系：

Q1=Q2=…=Qq

(3)

(4)

2.2 安装姿态标定法

在描述物体姿态的方法中，除方向余弦矩阵外，还有一种“角度给定法”[16]。角度给定法可分成RPY角和欧拉角两类，其中后者更常用。欧拉角有12种组合，安装姿态标定法以其中一种组合描述姿态，完成测量系统的安装姿态标定。

2.2.1 安装姿态描述

根据传感器坐标系相对末端坐标系的转动顺序，安装姿态以z-x-y欧拉角描述。令绕Zs轴转动的欧拉角为θ，绕Xs轴转动的欧拉角为β，绕Ys轴转动的欧拉角为α，如图3所示。

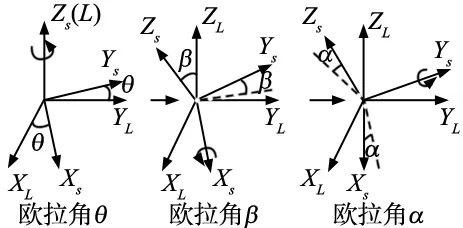
图3 安装姿态描述

2.2.2 安装姿态分析

(1)欧拉角α：以平面为对象，将高精度平面放置与末端坐标系OLXLYLZL的XLOYL平面平行。为了保证平面满足平行的要求，令机构沿Xb轴或Yb轴运动，调节高精度平面使其在传感器坐标系的x=0处测点始终满足Z向差值|z2-z1|≤ε(ε为波动范围，根据实际平面条件设置)，如图4所示。

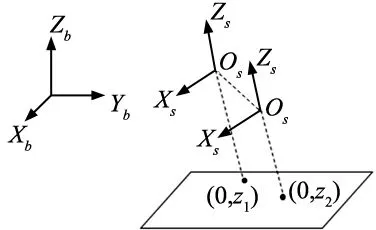
图4 平面调节过程

线激光传感器测量该平面得到由数据点(xi,zi)构成的轮廓线(i=1,2,…,n1)，如图5a所示。

设直线拟合方程为z=a1+b1x，根据最小二乘法，得到目标函数为：

(5)

由此求出直线参数a1、b1的大小，再根据图5b所示的直线斜率b1与欧拉角α的关系，得到α的大小为：

α=|arctan(b1)|

(6)

欧拉角α的正负判断方法是直线上偏为正，下偏为负。

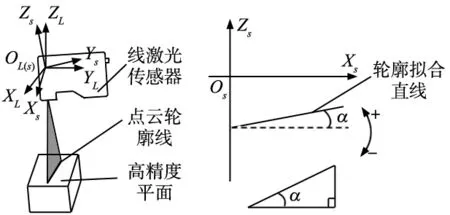
(a) 平面测量(b) 直线与α的关系

(2)欧拉角β：在欧拉角α标定的基础上，传感器坐标系的Xs轴与末端坐标系的XLOLYL面共面。在基坐标系Zb轴方向上选择位置1、2，将位置2处传感器坐标系的Zs2轴延长至位置1处传感器坐标系的Xs1O1Ys1平面交于A0得到ΔO1O2A0，则欧拉角β的大小可由∠O1O2A0表示，如图6a所示。欧拉角β的正负判断方法是传感器Zs轴左偏为正，右偏为负，如图6b所示。

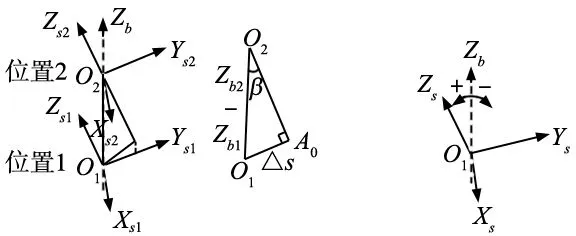
(a) 欧拉角β大小(b) 欧拉角方向判断

O1O2长度等于位置1、2的基坐标系Zb轴的坐标差Zb2-Zb1，O1A0长度Δs由交点A0到Ys1轴的距离ΔXs与到Xs1轴的距离ΔYs确定，即：

(7)

因此，得到以下关系：

(8)

Zb1与Zb2可直接从机构坐标获取，分析出ΔXs与ΔYs的值即可得到欧拉角β的大小。首先，分析ΔXs的大小。将标准球放置合适并固定，在位置1处测量球面得到在传感器坐标系下的截面圆轮廓点数据，圆拟合得到圆心坐标C1；将传感器移动到位置2，同理可得圆心坐标C2，如图7a所示。

截面圆轮廓数据拟合采用最小二乘法，设拟合圆方程为：

(9)

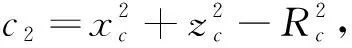
(10)

F分别对a2、b2、c2求偏导数并令其等于0得到偏导数方程组f2，求解方程组f2可得F的最小值，若令：

(11)

则方程组f2的解为：

(12)

则圆心坐标(xc,zc)与半径Rc可表示为：

(13)

由最小二乘圆拟合方法得到位置1的圆心坐标C1(xc1,zc1)和半径Rc1，位置2的圆心坐标C2(xc2,zc2)和半径Rc2，则ΔXs的大小为：

ΔXs=|xc2-xc1|

(14)

其次，分析ΔYs的大小。ΔYs可由球心在位置1、2传感器坐标系的Ys轴坐标差值表示。但截面圆拟合半径误差较大，以半径Rc1、Rc2与球基准半径R0计算球心坐标[10]不准确，从而难以得到准确的ΔYs值。由于线激光传感器安装姿态的欧拉角通常较小，可由球心在机构Yb轴坐标的差值近似替代ΔYs值。在位置1处通过机构Yb轴运动使传感器扫描球面，将Yb轴坐标与传感器Xs、Zs轴坐标结合构成球面轮廓数据(xsk,ybk,zsk)，k=1,2,…,n2，如图7b所示。

(a) 截面圆测量 (b) 球心测量

采用最小二乘法进行球面拟合，原理与最小二乘圆拟合方法类似，由此得到位置1处的拟合球心为(xQ1,yQ1,zQ1)，半径为RQ1。在位置2处同理得到拟合球心为(xQ2,yQ2,zQ2)，半径为RQ2。则可以得到ΔYs的大小为：

ΔYs≈|yQ2-yQ1|

(15)

从而欧拉角β大小为：

(16)

实际标定过程中，可以多次改变位置1、2测量球心来计算欧拉角β，剔除其中的粗大误差并几何平均计算得到最优值，能够有效减小机构几何误差影响。

(3)欧拉角θ：在欧拉角α，β标定的基础上，末端坐标系OLXLYLZL与传感器坐标系OsXsYsZs之间仅存在欧拉角θ。在位置3处使线激光传感器测量球面得到截面圆轮廓数据(xm,zm)与当前位置基坐标系的Yb轴坐标yc3(m=1,2,…,n3)。对数据点(xm,zm)进行最小二乘圆拟合，得到圆心坐标C3(xc3,zc3)；位置4同理可得圆心坐标C4(xc4,zc4)与该位置基坐标系的Yb轴坐标yc4，如图8a所示。

根据末端坐标系与传感器坐标系的几何关系构建ΔC3C4B0，如图8b所示。欧拉角θ大小为：

θ=sin-1(|xc4-xc3|/|yc4-yc3|)

(17)

欧拉角θ正负判断方法是Ys轴上偏为正，下偏为负。为减小机构几何误差的影响，多次改变位置3、4测量计算欧拉角θ求解最优值。

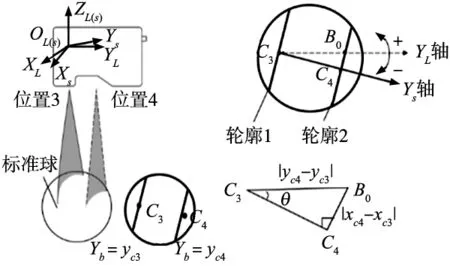
(a) 截面圆测量 (b) 坐标系的几何关系

2.3 安装姿态标定

根据“从左到右”的原则排列三次旋转对应的矩阵R(z,θ)、R(x,β)、R(y,α)，从而表示安装姿态的旋转矩阵Rs为：

(18)

式中，R(z,θ)、R(x,β)、R(y,α)分别为：

将上述分析得到的欧拉角α、β、θ代入式(18)解算旋转矩阵Rs，根据式(2)完成线激光传感器测量系统的安装姿态标定。

3 实验验证与分析

3.1 系统标定试验

标定实验中，运动载体为X、Y、Z三轴移动机构，其单轴重复定位精度≤5 μm、线激光传感器型号为GOcator2420，其技术指标有：测量范围为25 mm，X向分辨率为0.014 mm，Z向分辨率为0.001 8 mm、标定靶标为φ30 mm且圆度≤1 μm的哑光陶瓷球和1级精度的哑光量块，装置如图9所示。

图9 标定实验装置

采用定点变位姿法进行标定实验。分别改变移动机构的X、Y、Z轴坐标值6次，然后对固定的标准球测量，得到18组机构坐标与传感器坐标系下的球截面圆心坐标与半径，由此求出传感器坐标系下的球心坐标，其中的6组数据如表1所示。

表1 定点变姿法实验数据 (mm)

由18组数据求出表示传感器安装姿态的旋转矩阵Rs1为：

采用安装姿态标定法进行标定实验。实验得到表示传感器安装姿态的欧拉角α、β、θ具体数值，如表2所示。

表2 安装姿态角数据 (°)

由三个欧拉角得到表示传感器安装姿态的旋转矩阵Rs2为：

3.2 误差验证实验

测量系统坐标系中的坐标点绝对位置较难确定，为了验证标定精度，线激光传感器测量系统分别以上述两种方法标定后，对一组数据点之间的空间距离进行测量，并与基准距离比较得到测量误差，以此评价标定效果。

图10 验证实验装置

数据点通过行程为25×25×10 mm的X、Y、Z三轴微调平台与直径为12.01 mm的基准孔工件实现，其中微调平台X、Y、Z轴的分辨率均为0.01 mm、精度<0.03 mm。将基准孔工件固定在微调机构上，如图10所示。

通过微调平台的X、Y、Z轴构建坐标系，以初始位置的基准孔坐标为参考点，依次沿坐标系X轴方向改变10次位置、Y轴方向改变10次位置、Z轴方向改变4次位置及X、Y、Z轴同时改变3次位置得到27个全局坐标系下的圆心数据点，数据点到参考点的基准距离由微调平台坐标计算得到。为了减小基准孔测量误差影响，每次测量圆孔的区域基本保持不变，并以相同的数据处理算法进行去噪处理、圆孔轮廓提取及圆拟合。

由上述两种方法分别标定后的测量系统对27个位置的基准孔测量，得到各位置的基准孔测量半径及其与参考点的测量距离，与基准距离比较得到两种方法标定后的距离测量误差，如图11和图12所示。

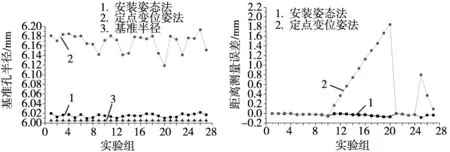
图11 基准孔测量半径图12 距离测量误差图

对数据进一步处理分别得到定点变位姿法M1与安装姿态标定法M2的数据点距离测量误差绝对值的最大值Emax、最小值Emin和均方根误差Erms_d，以及27次基准孔测量半径的均值Rave及其均方根误差Erms_r，如表3所示。

表3 测量结果分析 (mm)

根据图11、图12和表3可知，定点变位姿法标定后的距离测量误差不稳定，存在误差敏感方向且误差较大，而安装姿态标定法标定后的距离测量误差较稳定且误差较小；安装姿态标定法的距离测量均方根误差为0.039 mm、圆孔测量半径均方根误差为0.011 mm，比定点变位姿法的0.803 mm与0.162 mm减少了0.764和0.151。结果表明，安装姿态标定法精度优于定点变位姿法，且基本达到现有研究[4]标准偏差在0.065 mm以内的精度水平，可满足零件加工检测需求。

另外，测量结果误差来源除了标定误差，还有X、Y、Z三轴移动机构与微调平台的几何误差、圆孔测量误差以及环境噪声等。可通过机构误差补偿等措施，减小这些因素对测量结果的影响，进一步提高测量精度。

4 结论

本文针对多轴移动机构与线激光传感器构建的测量系统提出了一种安装姿态标定方法，解决了标定精度不足的问题。以欧拉角描述了测量系统的安装姿态，以平面和球面为靶标分析了欧拉角大小，并构建了姿态矩阵完成标定。测量结果表明，该方法标定精度较高，达到了现有研究的精度水平，可满足相关需求。