光纤光栅传感器在柔性机械臂位姿检测的应用*

于志宏，张 巧

(1.衡水职业技术学院计算机系，衡水 053000；2.河北工程技术学院计算机系，石家庄 050091)

0 引言

柔性传感器是对柔性机械臂实现闭环控制具有重要作用，现有的位姿检测方法有磁场检测、电检测、视觉检测和FBG检测。相对于高刚度的电检测，电磁干扰的磁场检测，以及视觉检测，简便轻巧且可嵌入的FBG具有高灵敏度和快速响应，具有广泛的应用前景[1-2]。

基于光纤光栅的形状传感器在工业领域的应用是目前研究的重点。卢团良等[3]利用光纤光栅传感器搭建了机床主轴轴承预紧力的监测系统，通过仿真和实验表明了光栅传感器监测能力的有效性。何为等[4]通过光纤光栅传感器实现了轴瓦温度的监控，提高了温度监控的准确性。胡娜等[5]针对梁式龙门机床的受力特点，采用光纤光栅传感器实时监测了其结构的变形，通过监控的数据重构了变形量，并通过实验验证了该测量方法的有效性。因此，光纤光栅在位姿检测中的应用前景广阔。

由于大多数柔性机械手都是仿生机器人，一些学者采用实验方法建模。陈志勇等[6]针对柔性机械臂的控制问题，通过奇异摄动法提出了自适应优化控制算法，该算法具有较强的自适应性和鲁棒性能，仿真结果验证了柔性机械臂在运动控制方面具有合理性。周晟等[7]针对柔性机械臂在外界干扰的情况下，利用拉格朗日法构建了机械臂运动学模型，提出了高阶滑模控制策略，并通过实验仿真表明了所提方法在控制过程中能有效消除系统的抖振现象。刘晓敏等[8]针对仿人手柔性机械臂的物体抓取控制，进行了不同压力下的柔性机械手的运动过程控制实验，通过实验表明柔性机械臂能够在一定尺寸范围内完成物体的抓取。

本文的重点是分析非线性柔性材料对姿态的影响，基于光纤光栅传感器，提出了柔性机械臂位姿检测优化模型，并通过实验仿真验证了优化模型对大变形柔性机械臂空间姿态检测的正确性。

1 螺旋光纤光栅传感原理

图1 螺旋型光纤光栅的传感原理

轴向伸长率/压缩率的变化包括拉伸变形和弯曲变形。将εij分为轴向拉伸应变εij1和弯曲应变εij2，可以通过式(1)～式(5)计算得到：

(1)

(2)

εij=(1+εij1)(1+εij2)-1

(3)

(4)

(5)

式中，pe表示光弹性系数；a是螺旋角；μ是泊松比。在截面i中，挠度角φi，曲率ki，以及弯曲角度θi等变形参数，可由式(6)～式(8)计算：

(6)

(7)

(8)

2 计入轴向变形的运动学模型

基于常规分段恒定曲率(CPCC)的运动学模型的截面坐标变化如图2所示，(XA,YA,ZA)表示基准坐标，与FBG坐标一致。(x0,y0,z0)为第一截面的初始坐标，(XB,YB,ZB)表示弯曲面的坐标，(xi,yi,zi)为截面i的终点坐标，(XA′,YA′,ZA′)表示末端中心的实际坐标。变换矩阵T表示(XA,YA,ZA)转换到(XA′,YA′,ZA′)，可以描述各截面的形状和末端中心的位姿关系，由式(9)～式(10)计算：

(9)

(10)

图2 基于CPCC的运动学模型示意图

非线性柔性材料通过末端的运动和变形影响第一截面的被动变形，以XBOZB弯曲面任意位置为例，分别采用仿真和视觉进行位姿检测，如图3所示，同样其他坐标的结果相同。

(a) 检测偏转角度的仿真 (b) 检测偏转角度的视觉

可以看出(x0,y0,z0)和(XB,YB,ZB)并不一致，两者在不同位置上有不同的偏转角度δ，这是由于材料的变形是不均匀的，使得第一截面因末端变形而引起被动变形。然而，现有文献[9-11]研究了基于CPCC的运动学模型，但并没有考虑δ的影响。基于此，本研究的改进型分段恒定曲率运动学模型如图4所示。

图4中的坐标(XA,YA,ZA)、(xi,yi,zi)和(XA′,YA′,ZA′)与图2相同，截面i的变形信息如图5所示。

图4 改进后的运动学模型坐标 图5 第i截面的变形图

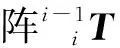
(11)

柔性机械手的变形参数(x,y,z,α,β,γ)可以通过式(12)～式(14)计算得到：

(12)

x=px,y=py,z=pz

(13)

(14)

式中，

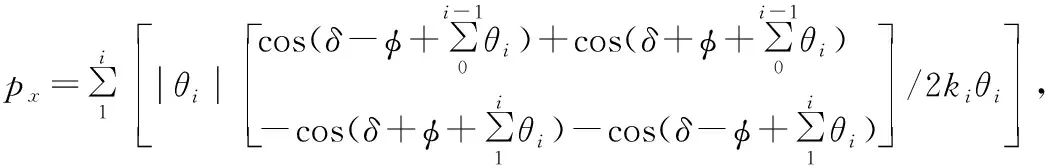
图6 柔性机械臂示意图

螺旋槽可以有效降低FBG布置的难度，在3D打印技术的帮助下，柔性机械手可以使用橡胶类材料制成，柔性机械手的相关参数如表1所示。图6所示为柔性机械手的物理图像，柔性机械手的末端由三向导轨驱动，能够到达空间中的任意位姿。FBG询问器(JT-2017-01)在USB通信模式下工作，其采样频率为1000 Hz。从采集FBG数据到获得各截面变形参数的时间小于5 ms。此外通过开发基于机器视觉的标定检测装置和算法[12-13]，以实现相应的检测。通过CPCC和IPCC两种模型检测同一位姿，将其结果与视觉结果进行比较，在此基础上根据优化信息对柔性机械臂进行位姿重构。

表1 柔性机械手的相关参数

3 改进模型的实验分析

为了证明IPCC的正确性，设计了一种表面具有0.86 mm深度双向螺旋槽的柔性机械手。由于δ不能从图4的几何关系直接计算出来，δ和θ1的关系可以通过标定过程中的视觉检测获得，如图7所示。

图7 δ和θ1的关系

将柔性机械手根据控制指令到达期望位置，获取图像，根据相应的时间确定每个截面的FBG数据。根据柔性机械臂的变形特点，开发了相应的图像处理算法来提取中心轴线。以某位姿为例，提取中心轴线的步骤如图8所示。

(a) 原始图像(b) 提取目标 (c) 提取中心线

两种模型和视觉检测到的端点坐标如图9所示，其中中间的虚线代表视觉、左侧的实线代表CPCC的结果，与虚线几乎重合的实线代表IPCC的结果。

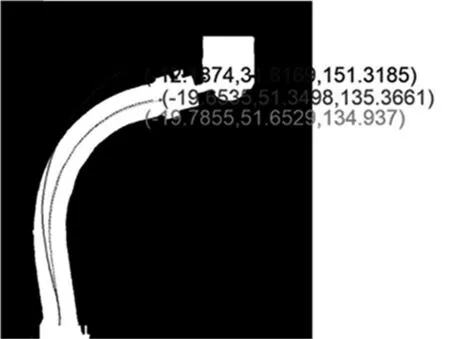
图9 两种模型的视觉效果比较

比较两种模型检测到的实验结果，表2描述了两个模型和视觉检测到的末端坐标值情况，两种模型检测的10个端点坐标的误差比较如图10所示。

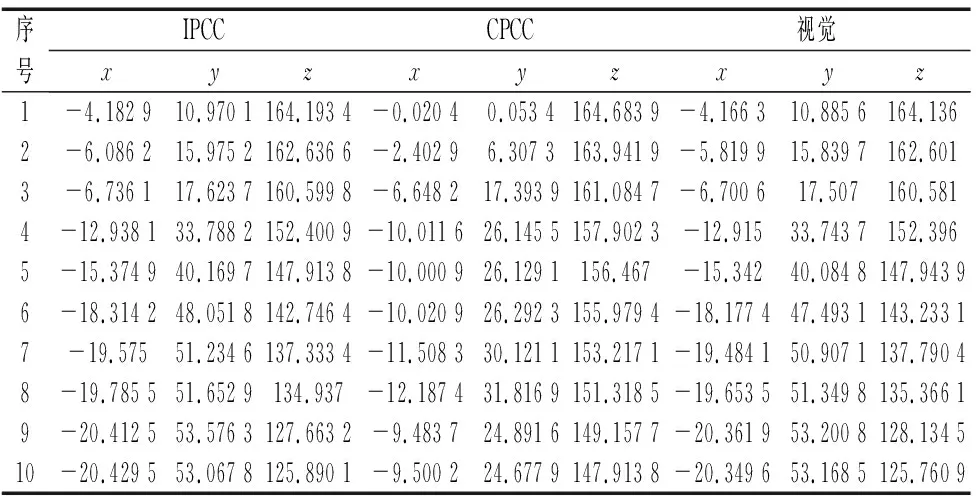
表2 坐标值检测值的对比 (mm)

表3 欧拉角检测误差对比 (%)

从图10可以看出，使用IPCC的末端坐标误差约为0，其最大值为0.753 5 mm，比CPCC减小了98%。实验的下一部分是关于末端的欧拉角的比较，表3分别描述了两种模型与视觉之间的欧拉角误差情况，欧拉角的比较如图11～图13所示。

图10 末端坐标位置 误差比较图11 不同模式下欧拉角 α的比较

图12 不同模式下欧拉角 β的比较图13 不同模式下欧拉角 γ的比较

从图11～图13可以看出，CPCC和IPCC两个模型检测到的欧拉角α和γ结果基本相同，其绝对值相等，误差小于0.11%。这是因为对于Z-Y-Z中的欧拉角α和γ，仅与表2中的φ有关。与α和γ相比，IPCC对β的影响更大。IPCC 对β的结果更接近于图12，β的误差不超过1%，除6号端点外，最大误差的绝对值约为CPCC的1/37。

在这个实验中，一个可能影响β测量的误差来源是柔性机械手的第三截面，第三截面在变形过程中被拉伸，使得半径变小，波长减小。但是最大变形位置到末端的距离比光栅到末端的距离更近。压缩光栅的位置，使得半径和波长增大，从而使该截面的弯曲角度增大，从而欧拉角β更大。为了进一步解决实验中出现的问题，将光栅的位置向上移动或增加第三截面部分的光栅数量，以提高检测精度。

实验结果表明，IPCC检测的变形参数具有较高的精度，利用获取的各部分变形参数重建柔性机械臂的空间位姿，部分结果如图14所示，可以看出重建的柔性机械臂空间位姿具有较高的精度，能为实现反馈控制提供可靠的反馈数据。

(a) 弯曲平面(视觉)

4 结论

针对大变形柔性机械手的姿态检测问题，在传统的分段恒定曲率运动学模型(CPCC)模型的基础上，提出了改进型分段恒定曲率运动学模型(IPCC)的姿态检测方法。该方法适用于轴向伸长/压缩的光纤光栅传感原理，考虑了非线性柔性材料变形而引起的附加变形。实验结果表明，改进型分段恒定曲率运动学模型(IPCC)可以提高姿态检测的精度。本研究为今后对柔性机械手的建模和柔性传感器的研究奠定了基础。然而，由于模型中缺乏扭转应变数据的获取，研究受到了限制。下一步的建模工作需要通过优化扭力标定装置来验证，包括拉伸、弯曲和扭转应变，从而更好地描述柔性机械臂的实际运动。