基于时序混合密度网络的超短期风电功率概率预测

2022-07-26董骁翀孙英云蒲天骄王新迎

电力系统自动化 2022年14期

董骁翀，孙英云，蒲天骄，王新迎，李烨

（1. 华北电力大学电气与电子工程学院，北京市 102206；2. 中国电力科学研究院有限公司，北京市 100192）

0 引言

随着中国“碳达峰·碳中和”目标的提出，风力发电将成为绿色低碳能源结构转型的重要支撑。由于风力发电受一次能源风能的影响，其出力存在不确定性。因此，精确可靠的概率预测是量化风电出力不确定性的必要工具，也是推动新型电力系统发展的重要技术［1］。

概率预测方法根据表达形式可分为预测区间（prediction interval，PI）、分位数回归（quantile regression，QR）和概率密度函数（probability density function，PDF）。PI 预测包含对应置信区间的上下边界［2-3］。QR 预测采用分位数信息描述预测概率分布信息［4-5］。PI 和QR 预测仅提供区间信息，不能连续描述概率预测信息。PDF 预测可使用参数法对预测值的概率分布进行建模，也可通过非参数法的核密度估计或混合分布模型建立PDF［6-7］。

依据建模方法，风电概率预测可分为统计学方法和人工智能方法。统计学方法对历史信息与预测概率分布之间的函数关系进行显式建模，主要包含高斯过程模型［8］、马尔可夫链模型［9］、时间序列模型［10］、Copula 函数模型［11］等。随着风电概率预测中影响因素的多元复杂化，传统统计学方法难以有效量化相关因素。而深度神经网络具有良好的高维非线性映射能力，基于人工智能方法的概率预测近年来得到了广泛关注［12］。通过最大后验估计（maximum a posteriori estimation，MAP）或最大似然估计（maximum likelihood estimation，MLE）对神经网络进行训练可以实现PDF 预测［13］。贝叶斯神经网络在给定先验分布后通过变分推理训练实现MAP，但先验分布参数较难确定［14］。MLE 可作为神经网络损失函数引导网络拟合PDF 的参数［15］。

为了有效解决参数法适用性较差的缺点，混合密度网络（mixture density network，MDN）被提出用于拟合混合分布，灵活描述预测PDF［16］。MDN 能够有效结合各类网络结构实现风电概率预测。文献［17］融合卷积神经网络和门控循环单元提取时空特征，使用MDN 拟合混合高斯分布实现短期风电功率概率预测。文献［18］使用MDN 拟合混合Beta 分布，相比混合高斯分布能有效防止密度泄漏。文献［19］采用包含注意力机制的MDN 模型融合多元气象信息进行概率预测。现有研究中MDN 对子分布参数的提取依靠对网络输出参数的直接拆分，难以说明混合分布中参数提取的原理及在风电概率预测中的意义，缺乏可解释性。另外，风电功率的概率特征存在持续性，能为概率预测提供可靠信息，而现有风电概率预测研究中缺少对多时间尺度概率特征的提取与融合［20］。

针对以上问题，本文提出了一种基于时序混合密度网络（temporal mixture density network，TMDN）的超短期风电概率预测模型。TMDN 在输入层采用局部矩通道的预处理方法，从风电时序数据中提取局部概率特征作为网络的输入信息。并且TMDN 采用多层时序卷积结构提取多时间尺度的概率特征，通过混合Beta 分布推演概率预测，有效提高了模型的可解释性。算例将本文所提方法与现有方法进行了对比，表明TMDN 具有更高的预测精度。

1 混合密度网络

MDN 采用神经网络映射输入数据与混合分布参数之间的关系，从而实现对条件概率分布的拟合［21］。MDN 融合了人工智能与非参数估计方法的优势，混合分布通过多个子分布参数的灵活组合具有更强的拟合能力，并且神经网络可以映射高维非线性关系。

MDN 的基本结构如附录A 图A1 所示，以混合Beta 分布为例，采用全连接网络映射混合分布参数。输入层输入条件信息，输出层输出混合Beta 分布的权重参数ω与形状参数α、β。混合Beta 分布的概率密度函数为:

式中:xt=[xt-L+1，xt-L+2，…，xt]T，其中，xt为风电在t时刻的出力实测值；yt+K为风电在K步后的出力预测值；θ为MDN 中的网络参数；f(·)为MDN 的映射函数。

假设有n组风电实测数据作为MDN 训练数据，由输入值X=[x1，x2，…，xj，…，xn] 以及目标值Y=[y1，y2，…，yj，…，yn]构成训练集，是典型的监督学习问题。概率预测模型以X作为MDN 的输入，希望由MDN 输出参数构成的混合Beta 分布在目标值Y处概率值最大。设Y中的目标值均为独立分布，MDN 的损失函数l(θ|X，Y)可由对数似然函数lnP(Y|θ，X)表示，即

2 时序混合密度网络

2.1 时序数据局部矩通道

卷积神经网络的多通道具有提取不同特征的作用，但特征意义较为模糊。本文通过局部矩计算对时序数据进行预处理，提取概率特征明确的局部矩信息构建通道，为MDN 拟合预测概率分布提供有效的数据支撑。

局部矩信息可以反映局部数据的概率特征，通过局部矩信息的变化特征能够有效推演概率预测。定义时序数据的局部n阶矩为在一个长度为k的窗口内计算n阶矩。并通过窗口在时序数据上滑动，计算不同时刻点的局部矩。时序数据局部矩的计算过程如图1 所示。图中:xˉ为窗口内x的均值；μ1和μ2分别为局部一阶矩与局部二阶中心矩。

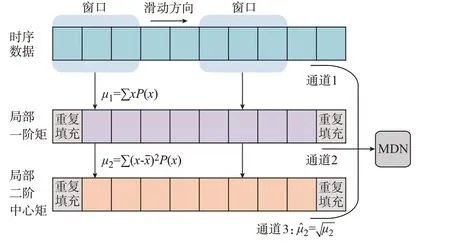
图1 时序数据局部矩通道Fig.1 Local moment channel of time sequential data

由图1 可知，时序数据经过局部矩计算后将得到一组新的时序数据。为了保证数据维度的一致性，在求解时需对时序数据两端进行重复填充，即使用时序数据的边缘值扩张数据尺寸。局部矩的求解与卷积的不同之处在于:局部矩的滑动窗口计算是固定的解析运算，不包含可学习的参数，具有明确的概率特征意义。不同局部矩信息表征着不同的概率特征作为MDN 的输入通道。为了保障输入数据的量纲一致性，取局部二阶中心矩的算数平方根μ̂2作为输入数据。

时序数据的局部矩反映了时序数据在概率特征上的变化情况。局部一阶矩描述的是时序数据在窗口内的平均值，其可以刻画非平稳时间序列的均值变化趋势。而局部二阶中心矩描述的是非平稳时序数据在窗口内的方差，可以刻画波动变化趋势。

2.2 时序卷积网络

时序卷积网络（temporal convolutional network，TCN）融合传统卷积网络结构提取时序数据特征［22］。相较于循环神经网络，TCN 能够以非循环形式处理时序数据，在避免梯度消失/爆炸问题的同时有着良好的并行计算能力。TCN 可以依据学习问题的形式灵活地设计网络结构，提取出针对目标的时序特征。本文模型设计中采用因果卷积运算:

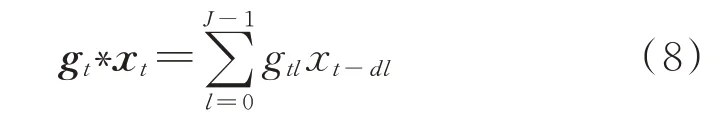
式中:gt为滤波器的输出，gtl表示其步长为l时的元素；“*”表示卷积运算；J为卷积核的长度；d为膨胀系数。从式（8）中可知，因果卷积的输出仅依赖之前的时序数据，具有严格的因果关系。

风电出力的概率特征具有持续性，因此未来风电出力的概率特征与历史特征存在相关性。若风电出力在短时间内存在较大波动，该波动特性在未来出力中具有一定持续性。但短时间内得到的概率特征难以表征更长时间尺度上的稳定性及趋势变化。因此，风电功率概率预测需要综合考虑多时间尺度的概率特征对预测点带来的影响。本文在结构设计中采用融合多层TCN 输出信息的结构，见图2。

从图2 中可知，顶层TCN 能够提取[t-7，t]时段内的概率特征，而底层TCN 仅能感知[t-1，t]时段内的概率特征。堆叠多层TCN 可以扩大网络在时序数据上的感受野，提取时间尺度更长的概率特征。为了融合多时间尺度的概率特征，模型将每层TCN 输出的尾部特征值作为一个子分布的参数特征。不同Beta 分布的参数特征来源于不同的TCN 层，从而MDN 的预测结果可以融合多时间尺度的概率特征构成混合Beta 分布。

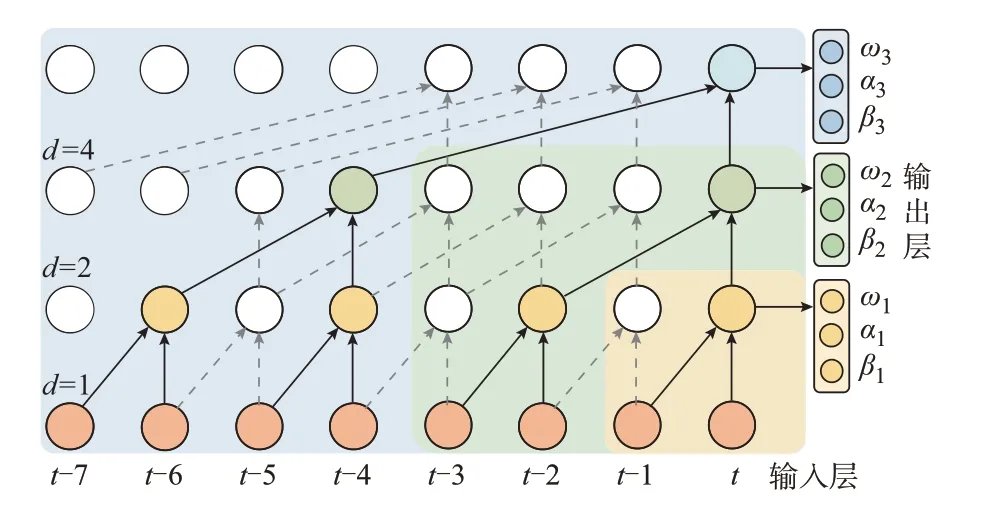
图2 TCN 示意图Fig.2 Schematic diagram of TCN

2.3 TMDN 结构

结合时序数据局部矩通道与TCN，本文提出了基于TMDN 的风电超短期概率预测模型，网络结构如图3 所示。

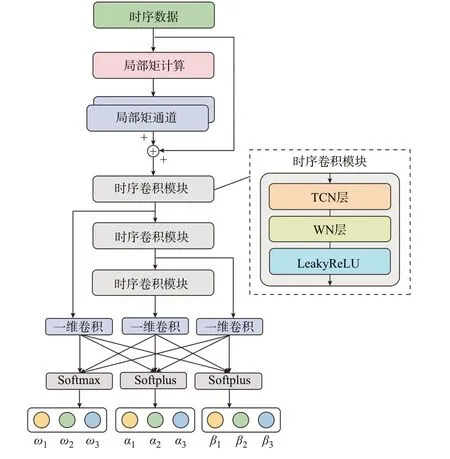
图3 TMDN 结构Fig.3 Structure of TMDN

首先，时序数据经过局部矩计算构建局部矩通道，结合原始时序数据作为TMDN 的输入信息。其次，TMDN 结构整合TCN 层、权重正则化（weight normalization，WN）层、激活函数LeakyReLU 作为时序卷积模块提取概率特征。TCN 层用于压缩时序维度并提取概率特征。WN 层将网络权重分解为标量和向量进行更新，加速收敛［23］。LeakyReLU 激活函数被用于提高网络的非线性拟合能力。最后，多个时序卷积模块提取的输出信息作为多时间尺度的概率特征被提取至输出层。经过一维卷积网络压缩至3 个通道，并将相应通道的权重和形态参数输入对应的激活函数获得满足条件的混合Beta 分布参数。

MDN 将以最大似然估计为目标进行训练。训练MDN 时取负对数似然（negative log-likelihood，NLL）函数作为损失函数。

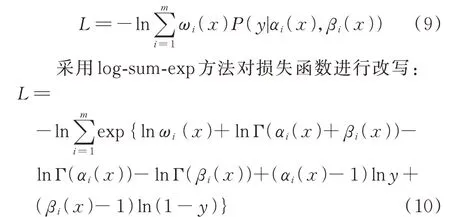
2.4 评价指标

本文采用平均绝对误差（mean absolute error，MAE）IMAE和均方根误差（root mean square error，RMSE）IRMSE作为确定性预测评价指标。并采用平均覆盖误差（average coverage error，ACE）和预测区间平均宽度（predict interval average width，PIAW）分析概率预测的可靠性和锐度性能，连续等级概率分数（continuous ranked probability score，CRPS）ICRPS被用于综合评价概率预测精度［1］。

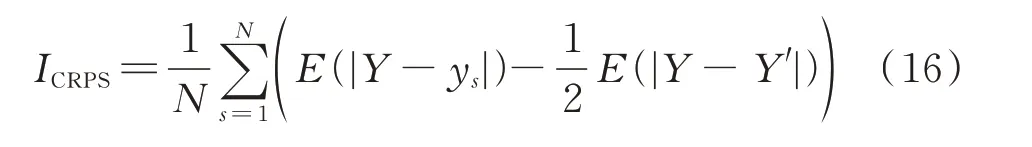
式中:Y和Y′为从概率密度函数P(y)中采样得到的独立随机变量；E(·)表示求期望值。ICRPS越小表明概率预测综合性能越好。

3 算例分析

3.1 算例概况

算例采用澳大利亚White Rock 风电场实测数据进行验证分析，风电场额定容量为175 MW，数据分辨率为15 min［24］。取2019 年1 月1 日至2020 年12 月31 日数据作为训练集，2021 年1 月1 日至2021 年6 月30 日数据作为测试集。

算例中的模型通过深度学习框架Pytorch 1.8.0搭建。计算机CPU为Intel Core i9 7900X（3.30 GHz），内存128 GB，显卡为NVIDIA TITAN V（显存12 GB）。算例将TMDN 模型与4 种概率预测模型从确定性预测与概率预测两个方面进行对比。

对比模型包括基于Gaussian 分布和Beta 分布的两种深度自回归（deep autoregressive recurrent，DeepAR）模型、基于混合高斯分布的MDN 模型（用FCN-GMM 模型表示）和基于混合Beta 分布的MDN 模型（用FCN-BMM 模型表示）。

3.2 模型训练分析

算例采用4 h 风电实测数据作为输入，单步预测未来15 min 至4 h 的风电功率。TMDN 模型中3 层TCN 的卷积核大小分别为1×2、1×2 与1×4，局部矩窗口宽度为3。模型训练参数设置训练次数为500 次，批数量（batch size）为500，学习率为0.001。为了对比模型的训练效率，5 种模型的训练时间见附录A 表A1。

算例在训练中设置了局部矩通道的对比模型。模型1 不附加局部矩通道，将原始数据直接输入模型训练。模型2 附加局部一阶矩通道和局部二阶矩通道。两种模型在20 次训练中损失函数的置信区间与均值见附录A 图A2。从图A2 可知，模型2 在训练中损失函数的置信区间更窄，且训练收敛后模型2 的损失函数均值更小。因此，局部矩通道能够有效提高网络的收敛性。

为了说明TMDN 模型结构提取多时间尺度概率特征的有效性，算例将TMDN 模型与FCNBMM 模型的混合Beta 分布权重进行对比，取[t-2，t]时段的局部二阶矩信息表征短时间尺度内风电功率波动情况，测试集分布权重与局部二阶矩信息的关系见附录A 图A3。依据TMDN 模型设置的卷积核大小和分布权重ω1(x)、ω2(x)、ω3(x)分别对应前30 min、1 h 和4 h 内的概率特征。从图A3（a）中可知，ω1(x)与风电功率波动呈现明显的正相关，当风电波动较大时，概率预测偏向于30 min内的概率特征。ω2(x)与风电功率波动呈现负相关，当风电功率波动较小时，风电概率预测更偏向于1 h 内的概率特征。而当风电功率较为平稳时，ω3(x)权重较大，风电概率预测偏向于更长时间尺度的概率特征。从图A3（b）可知，FCN-BMM 模型提取的权重与风电波动特征关系较为模糊，且不同权重对应的时间尺度在模型中也无法有效对应。因此，TMDN 模型在风电概率预测中能够提取并融合多时间尺度的概率特征，有效引导风电概率预测，具有更好的可解释性。

3.3 预测结果对比

概率预测模型经过训练后，采用测试集进行验证。基于5 种模型的概率预测方法在2021 年1 月12 日06:00 至12:00 未来15 min 的概率预测结果如图4 所示，展示了置信度为10%至90%的置信区间与实测值。从图中可知，基于5 种模型的概率预测方法均能较好地描述风电出力的不确定性。预测时段内风电场出力呈现上爬坡状态，06:00 时风电场出力为3.14 MW，09:00 时风电场出力为71.40 MW。

图4 概率预测置信区间Fig.4 Confidence interval of probabilistic forecasting

为了分析概率预测模型在不同风电出力情形中的预测效果，06:00 和09:00 时刻的预测概率分布图见图5，图中每张子图的上、下小图分别表示06:00和09:00 时刻的预测概率分布图。06:00 时刻风电出力较小，由于Gaussian 分布是无界分布，DeepARGaussian 模型和FCN-GMM 模型预测的PDF 存在密度泄漏。而09:00 时刻5 种模型预测的PDF 能够较好地包含在有效区间内。独立的Gaussian 分布在期望逼近0 时，其PDF 出现更为明显的密度泄漏。而Beta 分布是严格定义在区间（0，1）中的有界分布，能够在有效区防止密度泄漏现象。因此，在概率分布描述的范围上，Beta 分布相比Gaussian 分布具有一定优势。

图5 预测概率密度分布Fig.5 Probability density distribution of forecasting

为了定量对比预测模型，对比5 种模型在超短期内多个时间尺度的MAE、RMSE 及CRPS 来衡量确定性预测与概率预测的精度，如附录A 表A2 所示。从表A2 中可知，MDN 模型相比DeepAR 模型在概率预测上更为准确，其中TMDN 模型在各个时间尺度中各项指标均达到了最优值，在确定性预测与概率预测中均有着更好的精度。

本文进一步验证了概率预测模型的可靠性与锐度性能。5 种预测模型未来1 h 预测的ACE 指标及PIAW 指标见附录A 表A3 和表A4。从表A3 中可知，DeepAR-Gaussian 模型、DeepAR-Beta 模型的ACE 指标均大于0，表明其PICP 指标大于对应的置信度。MDN 模型相比DeepAR 模型有着更低的ACE 指标，可靠性更高。TMDN 模型的ACE 指标最贴近于0，在置信度为40%至90%时均获得了最小值。TMDN 模型的ACE 指标在30%置信度下达到最大负值（-2.23%），在40%置信度下达到最大正值（0.74%）。

从附录A 表A4 中可以看出，5 种预测模型的PIAW 指标随着置信度的升高均呈现上升趋势。DeepAR 模型的PIAW 指标高于MDN 模型。混合分布相比独立分布有着更强的灵活性，给概率预测结果带来更好的锐度性能。TMDN 模型的PIAW指标在20%至90%置信度下均达到了最小值。从ACE 和PIAW 两个指标综合分析可知，TMDN 模型有着更高的可靠性与锐度性能，能够更精确地反映概率预测信息。