气隙轴向静偏心对发电机定子-绕组受载及振动的影响

何玉灵，孙 凯，孙悦欣，唐贵基，白 洁

（华北电力大学机械工程系暨河北省电力机械设备健康维护与失效预防重点实验室，河北保定 071003）

引言

气隙偏心故障是发电机和电动机常见的一种机械故障，是指定转子间气隙不均匀，存在一边气隙多，另一边气隙少的现象［1］。根据气隙最小位置是否随转子转动而变化，气隙偏心可分为静态偏心、动态偏心，以及动静混合偏心三类［2］。气隙偏心会使气隙磁场畸变，引发定子和转子振动，加剧绕组的绝缘磨损［1-2］。当偏心量达到10%时，则认定偏心达到故障级别，须进行即时处理，防止其恶化并带来严重后果［3］。在实际中，动偏心大多由表面圆度不齐或转子受热弯曲所致［4］，其偏心程度相对较小，较难达到10%的故障阈值。而静偏心大多由导轴承偏移、定子铁芯变形等因素所造成，相对而言较容易达到10%的阈值门槛。

已有研究成果中关于气隙偏心的研究大多是针对气隙径向偏心。目前，学者们已对气隙径向静偏心故障下的气隙磁场变化，以及磁场畸变引发的二次参数变化进行了研究［5-10］。例如，文献［5-7］研究了气隙静偏心故障对于气隙磁场的频率和空间特性的影响；文献［8］则研究了气隙静偏心及定子匝间短路复合作用下的气隙磁场变化规律。这些文献的研究表明，在气隙径向静偏心故障下，气隙磁密曲线将呈现出类似平移的效果，使磁密的最大值增加，从而导致与磁密密切相关的二次参量发生变化。文献［9-10］研究了气隙静偏心故障对定子损耗、转子损耗的影响，发现偏心后定转子损耗将有所增加；文献［11］发现在气隙径向静偏心故障下转子的二倍频不平衡磁拉力及其径向振动将显著增加。

目前对气隙静态偏心的诊断大多基于转子振动特性［12］和基于安装在气隙内部的探测线圈感应电势变化［13］。由于对已投运机组安装探测线圈较为麻烦，现场技术人员更倾向于采用基于振动的方式来对该类故障进行监测。除了转子振动外，定子振动也包含有丰富的故障信息，有时甚至比转子振动更加有效［14］。文献［15］对在正常状态以及气隙静偏心故障下的定子受力进行了理论分析和实验验证；文献［16］对定子支路不对称发电机在气隙静偏心、转子匝间短路单故障及复合故障下产生的定子电磁力进行了研究；文献［17-19］研究了永磁同步电机在气隙偏心故障下的定子径向受力；文献［20］发现开关磁阻电机转子偏心时出现的单边磁拉力会使振动和噪声更加恶化。

事实上，除了径向偏心外，发电机还可能存在轴向偏心。例如水轮发电机由于水流的长期冲击致使转子产生一定的轴向位移，在轴向上形成一侧气隙多、另一侧气隙少的现象，即轴向气隙偏心。汽轮发电机和风力发电机转子由于也会受到轴向推力，在长期作用下也可能形成气隙轴向偏心，但其偏心量相对水轮发电机而言较小。

现有报道中关于发电机气隙轴向偏心的研究要比径向偏心少很多，已有的关于气隙轴向偏心的研究多集中在转子受力部分。例如，文献［21］通过三维有限元仿真与模拟实验，研究了无刷直流电机中轴向不平衡磁拉力的特性，表明永磁体相对于定子的轴向不对称是产生轴向不平衡磁拉力的主要原因；文献［22］利用保角变换对发电机端部电磁场进行解析，最后推出轴向电磁力与气隙轴向偏心的关系式；文献［23］研究了感应电机端部及通风槽的轴向不对称引起的轴向不平衡磁拉力，并利用电导纸模型模拟通风槽的电磁场；文献［24］研究了永磁步进电机在长时间运行过程中转子发生轴向偏移后产生的轴向不平衡磁拉力；文献［25-26］分析了不同气隙偏心故障对转子多向受力的影响；文献［27-28］提出了同步发电机的三维气隙偏心模型，计算了三维气隙偏心下发电机电磁转矩的变化规律与转子的振动特性。但以上文献均未对轴向偏心下定子和电枢绕组的受载及其振动响应进行分析。

由于力的相互作用，当气隙轴向偏心发生时，除转子会受到轴向磁拉力外，定子铁芯也将受到轴向磁拉力作用，安装于定子铁芯中的电枢绕组所受的电磁力也将发生变化而呈现出不同于正常工况的振动特性。作为补充，本文将分析气隙轴向静偏心下的同步发电机定子和绕组受载及振动特性，剖析绕组绝缘同时在定子振动变形挤压和自身振动响应下的磨损危险位置，并提出相应的处理建议。

1 理论解析

1.1 气隙轴向静偏心对磁密的影响

发电机的气隙磁密由气隙磁势和单位面积气隙磁导构成。轴向气隙静偏心主要通过改变气隙磁势来影响磁密。正常及气隙轴向静偏心下的定转子气隙如图1所示。轴向静偏心下电机径向气隙与正常相同，其单位面积的气隙磁导可写为：

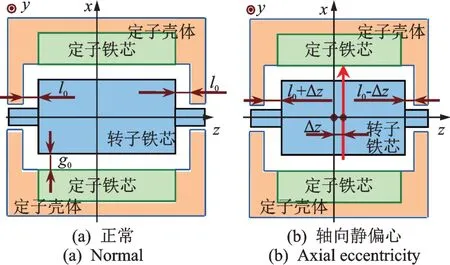
图1 轴向气隙静偏心前后的发电机气隙Fig.1 Air-gap of generator before and after axial eccentricity

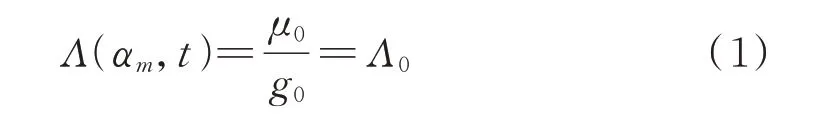
式中t为时间，αm为用于表征气隙周向位置的机械角度，μ0为真空磁导率，g0为径向气隙长度。可见轴向静偏心前后单位面积的气隙磁导为一常量。

气隙轴向静偏心下，气隙磁势将由图2（a）变化为图2（b），磁势的有效值减小。这也可以通过图1（a），（b）进行定性说明：轴向静偏心将使转子磁力线切割导体的有效长度减小，主磁势有一部分外漏于端部变为漏磁场。这种情况下，相当于发电机的定转子有效磁势均减小，从而使得气隙合成磁势也有所减小。

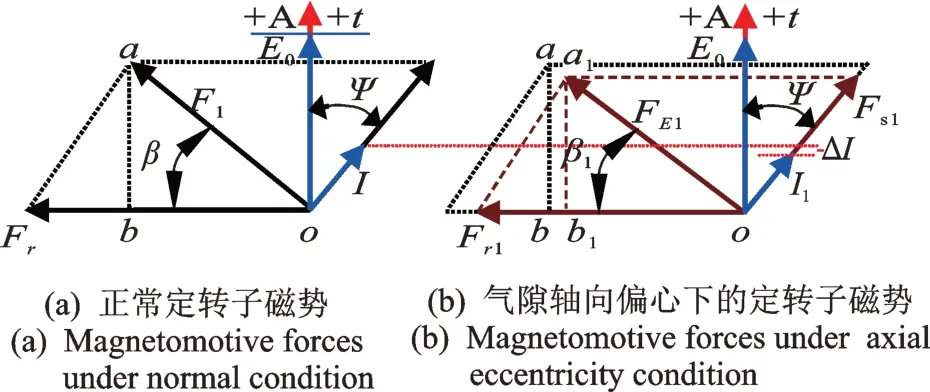
图2 轴向静偏心前后的同步发电机气隙磁势Fig.2 Magnetomotive forces before and after axial eccentricity

根据平行四边形法则，发电机气隙磁势可由主磁势与电枢反应磁势求得：

其中，

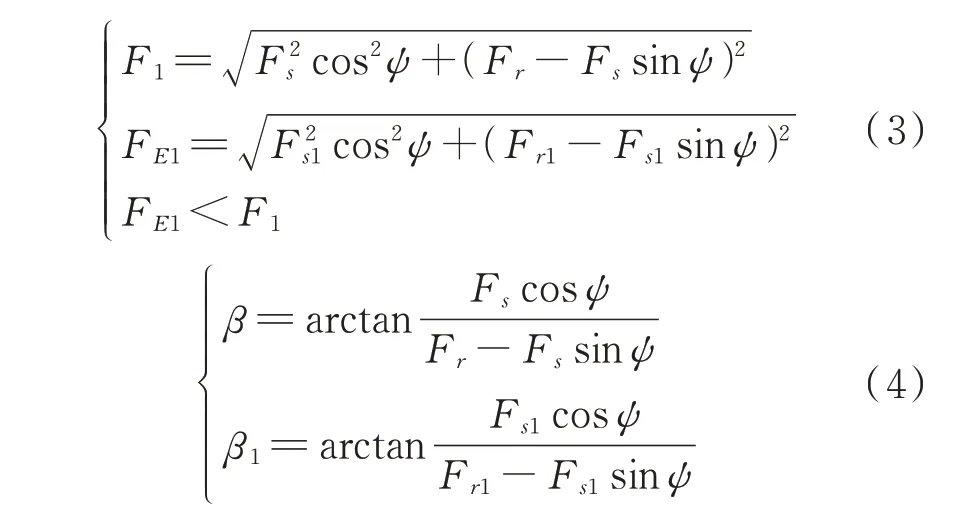
式中Fs，Fs1分别为故障前后电枢反应磁势，Fr，Fr1分别为故障前后主磁势，ω为转子角频率，ψ为发电机内功角，p为极对数。

由式（1）与式（2）相乘可得气隙磁密为：

式中FE1＜F1，相应对比结果如图3（a）所示，轴向静偏心下的气隙磁密呈现压缩态势，幅值降低。

发电机两端的端部磁密Be（αm，t）对称分布；而在轴向气隙偏心下，转子伸出端一侧的磁场将加强，而抽空端一侧的磁场将削弱，如图3（b）所示。

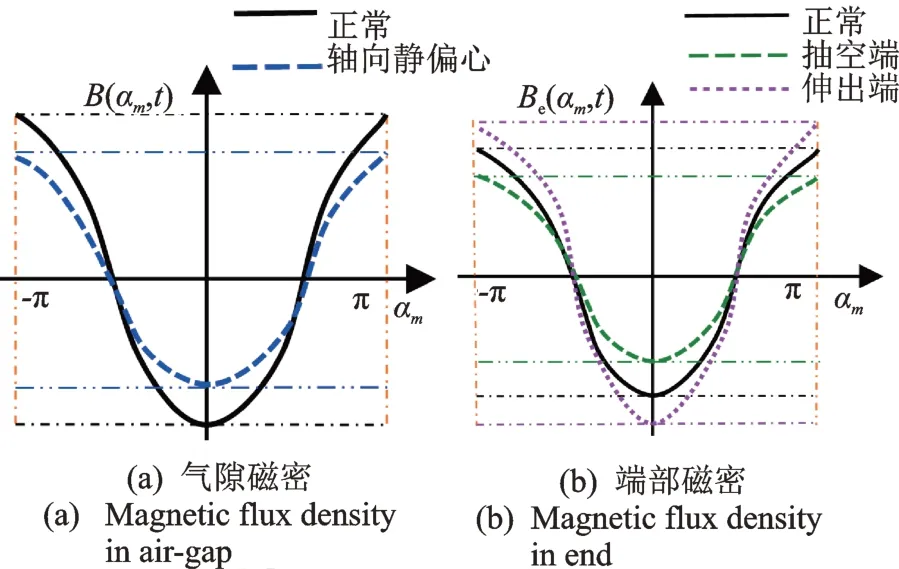
图3 轴向静偏心前后磁密变化Fig.3 The magnetic flux density variations

1.2 轴向静偏心前后定子受载及振动响应

1.2.1 轴向静偏心前后定子径向及轴向受载

（1） 径向受载

发电机定子铁芯在物理结构上是一个空心壳体，在径向方向的刚度较低，如图4（a），（b）所示。其振动响应的本质激励力为作用于定子内圆面的单位面积磁拉力，而非作用于整个铁芯的径向合力。这可以由图4（c）进行解释：图中单位面积磁拉力合力为零，但由于该单位面积磁拉力具有脉动性质，其幅值呈周期性变化，会导致铁芯做与单位面积力同频率的伸缩-扩张响应，即径向振动。可见，对于这种径向刚度较小的空心壳体结构，其本质激励源应为单位面积力。

图4 定子铁芯结构及其受载示意图Fig.4 Structure and load of stator core

气隙轴向偏心前后定子径向单位面积磁拉力为：

由式（6）可知，两种运行状态下定子均受到一个直流力和一个二倍频交流力作用。所不同的是，当气隙轴向静偏心发生时，由于FE1＜F1，径向单位面积磁拉力将减小；且随着轴向偏心程度的加剧，其单位面积磁拉力幅值也将逐渐削减，如图5所示。

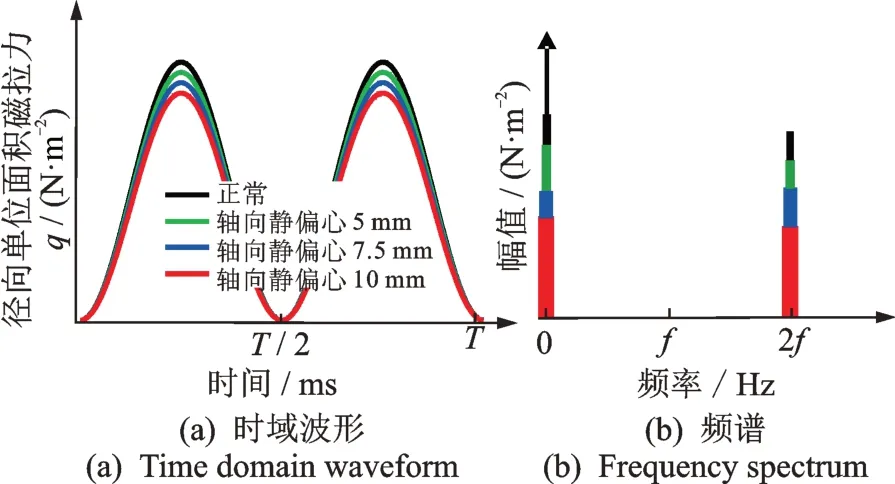
图5 单位面积磁拉力理论曲线Fig.5 Model result of magnetic pull per unit area on stator

（2） 轴向受载

由于定子铁芯在轴向上的刚度较大，故与径向振动有所不同，轴向上的单位面积磁拉力不足以使铁芯产生周期性的变形（即轴向振动）。因此，铁芯在轴向上的本质激振力为轴向不平衡磁拉力，如图4（d）所示。

定子轴向不平衡磁拉力应与转子轴向不平衡磁拉力大小相同、方向相反，根据文献［29］，定子轴向不平衡磁拉力可用转子轴向不平衡磁拉力公式表示：

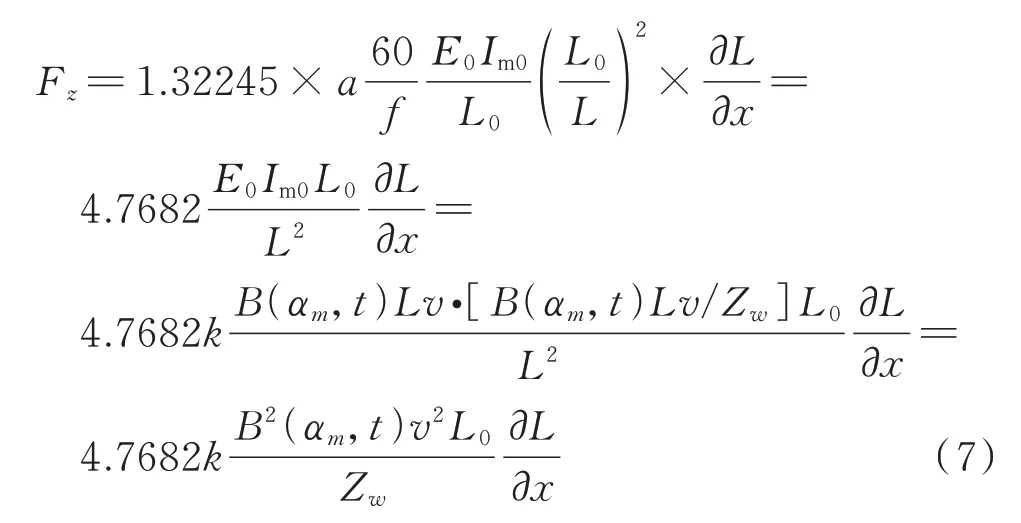
式中a为相数，f为电频率，L为转子的有效作用长度，L0为转子铁芯长度，E0和Im0分别为相电压和相电流的有效值，v为磁场旋转的线速度，Zw为绕组电抗，k为一个系数，表示通过B（αm，t）计算的瞬态电压电流与E0和Im0之间的关系，∂L/∂x为定转子有效长度比上定转子实际轴向长度的变化率，表达式如下：

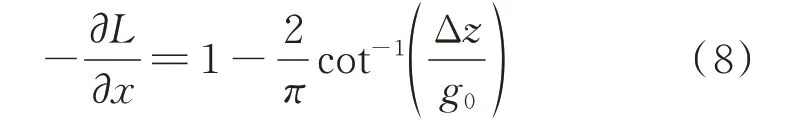
式中 Δz为轴向静偏心量。将式（5），（8）代入式（7），可得：

由式（9）可知，正常状态下的定子轴向不平衡磁拉力为零。发生气隙轴向静偏心后，定子铁芯在轴向上的不平衡磁拉力主要包含直流和二倍频分量，且随着轴向偏心程度加剧，这一轴向不平衡磁拉力幅值将逐渐增大，如图6所示。

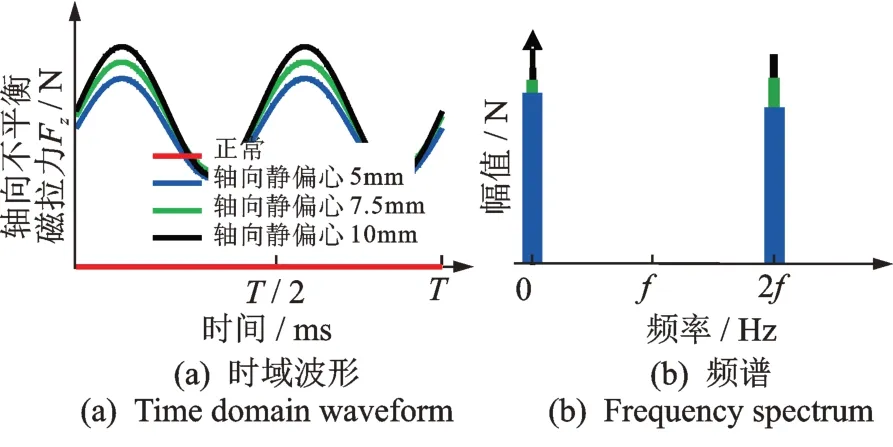
图6 轴向不平衡磁拉力理论曲线Fig.6 Model result of axial unbalanced magnetic force

1.2.2 轴向静偏心下定子振动响应解析

定子系统在径向上的力学模型如图4（c）所示，在轴向上的力学模型如图4（d）所示。针对两个方向的受力及振动响应关系，可列出其动力学方程为：

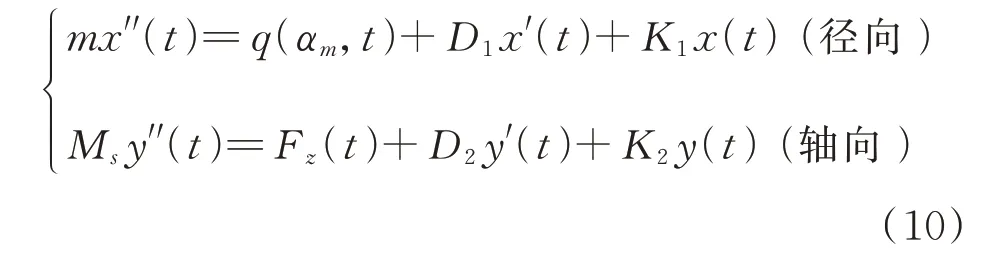
式中m为定子铁芯单位质点的质量，x（t）为单位质点的径向位移，x′（t）为径向位移的一次求导，即径向速度；x"（t）为位移的二次求导，即径向加速度；D1和K1分别为径向方向作用于单位质点的等效弹性系数及阻尼系数。Ms为定子铁芯的整体质量，y（t）为定子铁芯整体在轴向的位移，y′（t）为轴向位移的一次求导，即轴向速度；y"（t）为轴向位移的二次求导，即轴向加速度；D2和K2分别为轴向方向作用于铁芯整体的等效弹性系数及阻尼系数。

具体到磁拉力激励与一次强迫振动响应，径向的单位面积磁拉力为铁芯的径向激励，径向位移x（t）即为其振动幅值。由于单位面积磁拉力具有周期性，其对应的径向位移响应也会具有周期性，这种周期性位移即为径向振动。类似地，轴向不平衡磁拉力为激励，轴向位移y（t）反映其振动幅值。所不同的是，径向上的位移为铁芯单位质点的位移（不同周向位置对应的位移有可能不同），轴向上的位移则为铁芯的整体位移。在工程实际中，通常采用加速度传感器进行振动测试，其所测量反映的是位移的二次导数。

由式（6）与式（9）可知，径向单位面积磁拉力和轴向不平衡磁拉力同时包含直流和二倍频分量。根据激励与响应同频对应关系，直流力由于不具备脉动性质不会引发定子铁芯产生振动，但长期作用下可能导致铁芯产生一定的变形；二倍频交流力将使铁芯产生与其相同频率的振动，即二倍频振动。随着轴向静偏心量的增大，径向的二倍频振动幅值将有所降低，而轴向的二倍频振动幅值则将增大。

1.3 轴向静偏心前后定子绕组受载及振动响应

1.3.1 轴向静偏心前后定子绕组受载

将中心线位于y轴的绕组定义为1 号绕组，按照逆时针旋转的顺序对所有绕组进行编号，如图7所示，则各绕组的周向位置αmi可表示为：

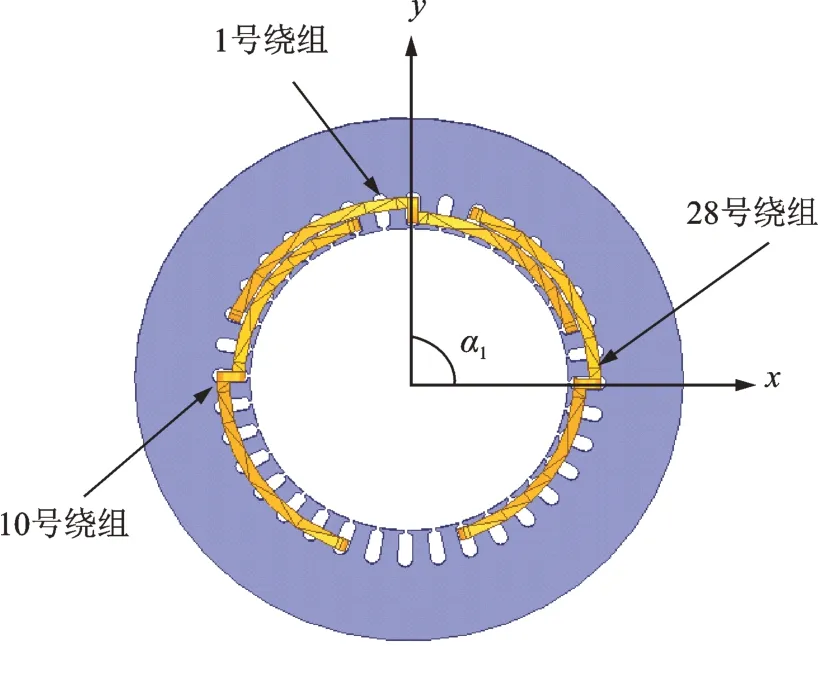
图7 定子绕组分布位置Fig.7 Distribution of stator windings

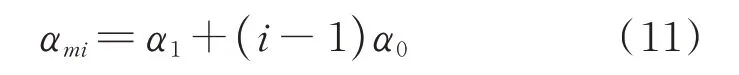
式中α1为1 号绕组中心线与x轴的夹角（本例为90°），α0为相邻定子两槽之间的夹角，i为绕组标号。

假设定子绕组中的电流分布均匀，且绕组截面处的磁场密度相同，不考虑定子绕组内部相互之间的磁密影响，则定子绕组的电磁力Fw为：

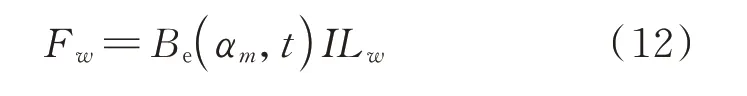
式中I为定子绕组的电流，Lw表示在垂直于磁场方向上定子绕组长度，由于绕组的实际变形量较小，可认为Lw为常值。

由欧姆定律和电磁感应定律，结合式（5）与（12），可得正常状态下第i个定子绕组的电磁力Fwi为：

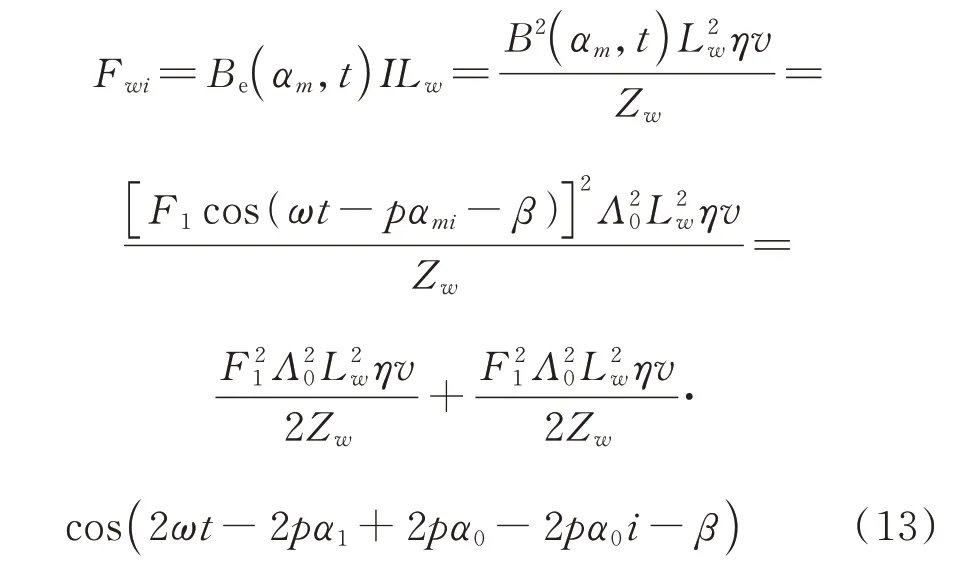
式中η为一个小于1 的系数，用于表征Be（αm，t）和B（αm，t）沿轴向积分结果之间的比例关系。

由式（13）可以发现，正常情况下定子绕组电磁力包含直流成分与二倍频成分，并且同一时刻定子绕组的电磁力和空间位置密切相关。

在气隙轴向静偏心下，由于两侧的端部磁场不对称，导致两侧的绕组受力不同。转子抽空侧的绕组受力FLsi与转子伸出侧的绕组受力FRsi可分别表示为：

式中BR为转子伸出侧端部磁密，FER为转子伸出侧端部磁势；BL为转子抽空侧端部磁密，FEL为转子抽空侧端部磁势。

由式（13），（14）可知，正常情况和气隙轴向偏心下的绕组电磁力均包含直流与二倍频分量。在气隙轴向静偏心下，由于转子抽空侧的端部磁密减小，导致其绕组受力也减小，且减小幅度随轴向静偏心程度加剧而增大。反之，转子伸长侧绕组受到的电磁力将增大，如图8所示。

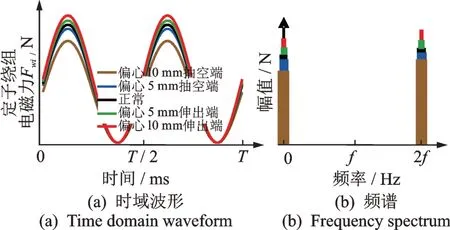
图8 定子绕组电磁力理论曲线Fig.8 Model result of stator winding electromagnetic force

1.3.2 轴向静偏心下定子绕组振动响应解析

由于定子端部绕组伸出于定子铁芯外部，在结构上相当于是悬臂梁，如图9（a）所示，其刚度较小，易在电磁力激励下产生振动并引发绝缘的磨损破坏，影响发电机的运行安全。将铁芯视为基础，绕组的等效力学模型如图9（b）所示，其对应的激励与响应方程为：

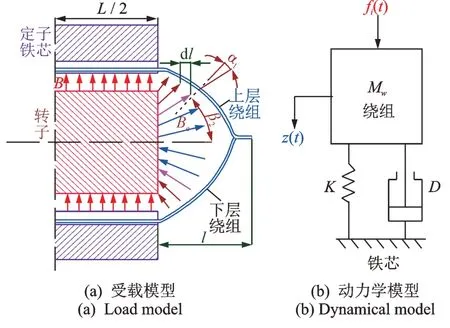
图9 定子绕组端部结构及其受载示意图Fig.9 Structure and load of stator end winding

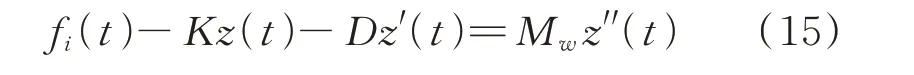
式中fi（t）为定子绕组受到的电磁力，K为刚度矩，z（t）为绕组振动位移，z′（t）为位移一次求导，即速度，z"（t）为位移二次求导，即加速度；D为阻尼（由绑扎带等部件提供），Mw为绕组质量。

根据激励与响应同频对应关系，由式（13），（14）可知，轴向静偏心作用下定子绕组将产生二倍频振动。随着轴向静偏心的增大，转子抽空侧绕组振动幅值将减小，但转子伸出侧的振幅将增大。

2 有限元计算与实验验证

2.1 有限元仿真计算

2.1.1 仿真模型设置

以新能源电力系统国家重点实验室CS-5 型故障模拟发电机为分析对象，发电机的关键参数如表1所示，建立的有限元物理模型如图10（a）所示，外部耦合电路模型如图10（b）所示。通过在物理模型中将转子沿轴向平移不同的距离来模拟不同程度的气隙轴向静偏心状态。仿真过程中设置励磁电流为2.5 A，每相负载为100 Ω 电阻和0.2 H 电感（功率因数为0.8）。通过在场计算器中依照式（6）对磁密取平方除以2μ0来获得定子单位面积磁拉力；绕组电磁力则直接从计算结果中获取。

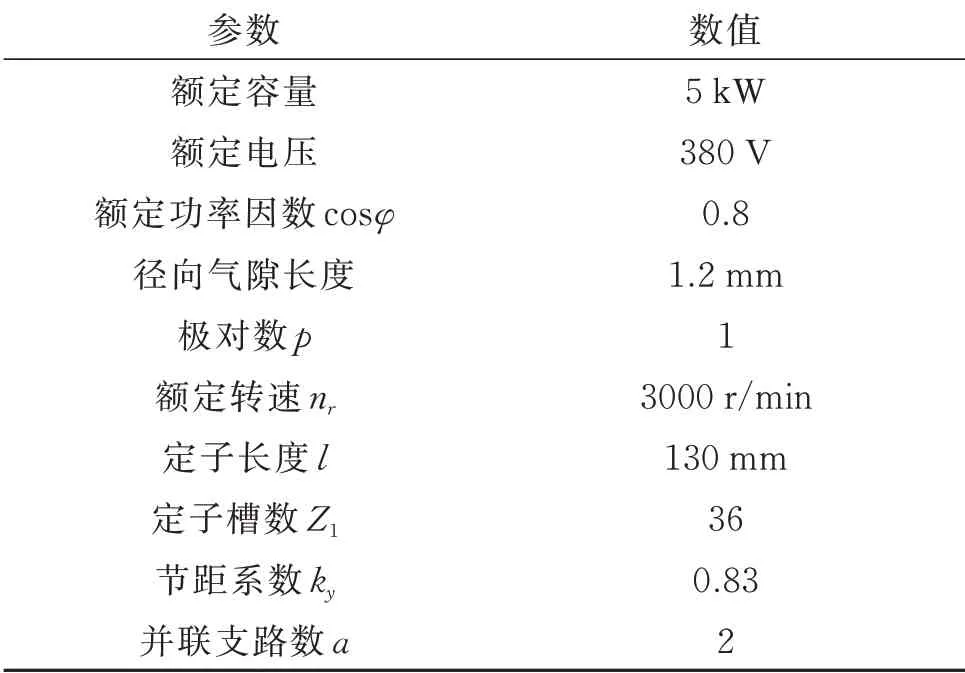
表1 CS-5 型发电机主要参数Tab.1 Main parameters of CS-5 prototype generator

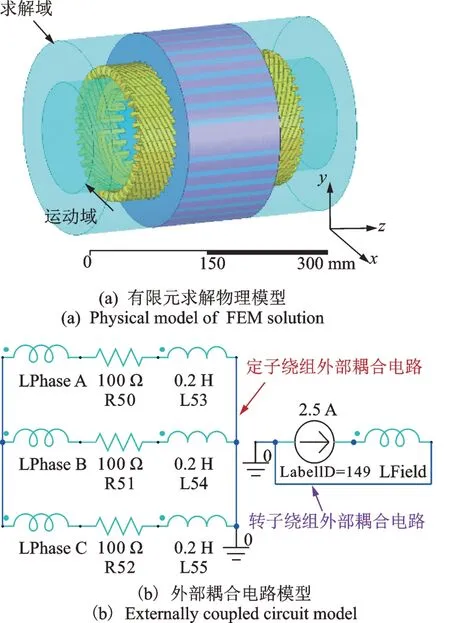
图10 仿真模型及电路Fig.10 Simulation model and coupled circuit

2.1.2 定子受载仿真结果分析

气隙轴向静偏心前后的径向单位面积磁拉力结果如图11 及表2所示。图11 中Normal 表示正常工况；Z5，Z7.5，Z10 分别表示轴向偏心5 mm，轴向偏心7.5 mm 和轴向偏心10 mm。MPPUA 表示定子铁芯受到的单位面积磁拉力。可看出单位面积磁拉力主要以直流和二倍频为主，另含有较小的四倍频成分；随着轴向静偏心的加剧，单位面积磁拉力减小，这与式（6）所得到的定性结论一致。

图11 中存在四倍频的原因是式（6）在对磁密的平方操作中只计及了主要的基波而忽略了高次谐波。若考虑高次谐波（如3次、5次等），则式（6）结果中还应含有其他各偶倍频成分，且它们的幅值变化趋势与二倍频一致。鉴于次数较高的谐波其幅值要小很多，故其单位面积磁拉力主要以直流和二倍频为主。

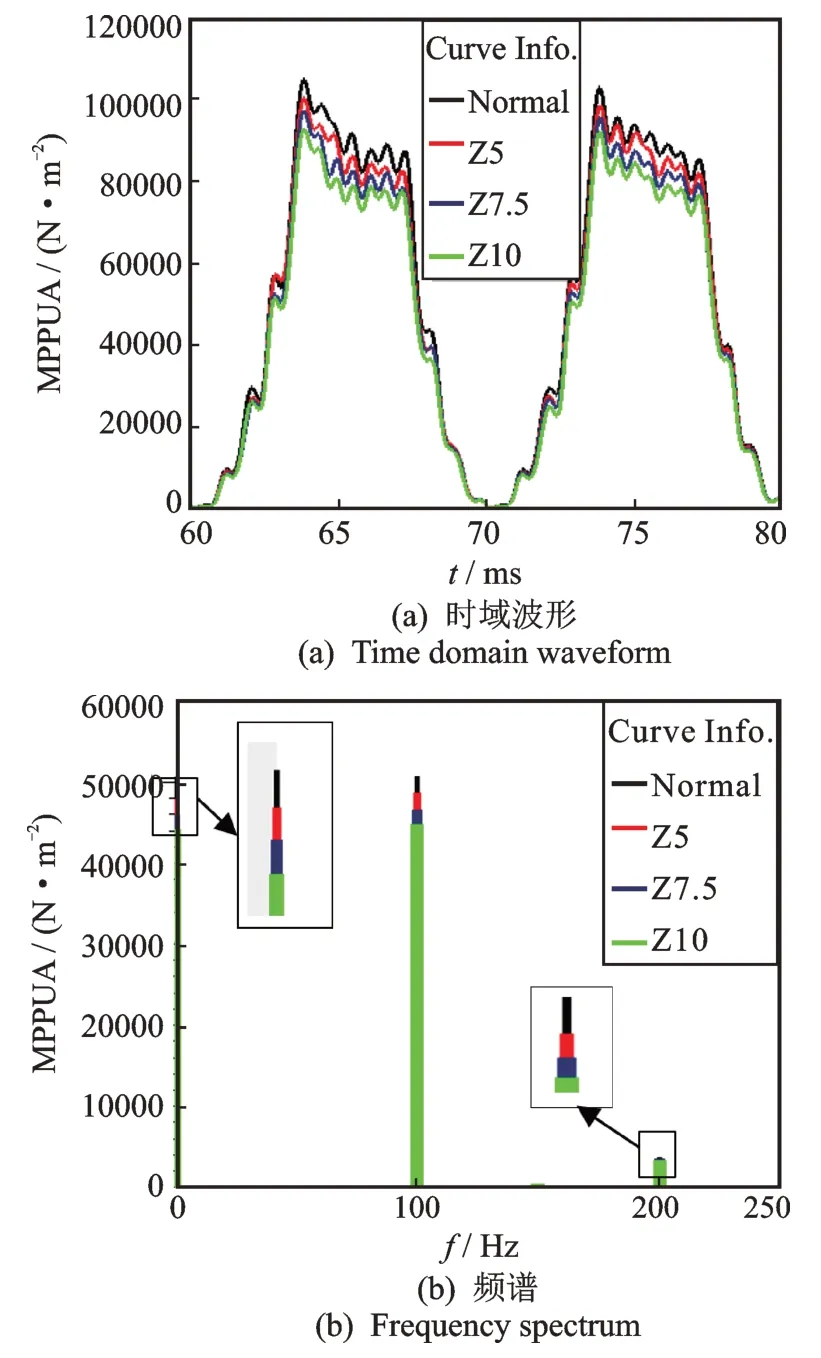
图11 气隙轴向静偏心前后的定子径向单位面积磁拉力Fig.11 Radial unit magnetic pull of stator before & after axial eccentricity

图12 及表3 为气隙轴向静偏心前后的定子轴向不平衡磁拉力仿真结果，图12 中，UMP-z 表示在z方向上的不平衡磁拉力。正常情况下轴向不平衡磁拉力基本接近于零，随着气隙轴向静偏心的发生，轴向不平衡磁拉力时域波形幅值、直流和二倍频幅值均有明显增长；轴向静偏心程度越大，其增幅越明显，这与式（9）的定性结论相一致。

表3 轴向静偏心前后定子轴向不平衡磁拉力幅值/NTab.3 Axial UMP amplitudes of stator before and after axial eccentricity/N

图12 气隙轴向静偏心前后的定子轴向不平衡磁拉力Fig.12 Axial magnetic pull of stator before & after axial eccentricity

2.1.3 定子绕组受载仿真结果分析

由于轴向静偏心下电机的径向气隙仍然均匀，同侧绕组在同一周期内的受力变化规律相同，故只取1 号绕组进行分析。图13，14 为气隙轴向静偏心前后1 号绕组电磁力仿真结果，各频率成分的幅值如表4所示。图中Normal 代表正常状态，Z5-L 代表气隙轴向静偏心5 mm 转子抽空侧的绕组电磁力，Z5-R 代表气隙轴向静偏心5 mm 转子伸出侧的绕组电磁力，Z10-L 和Z10-R 代表的意义类似。

由图13，14 可知，气隙轴向静偏心前后的绕组电磁力均为余弦分布，主要频率成分为直流与二倍频，同时含有较小的四倍频分量。这一结果与式（13）和（14）的定性结论相同，额外出现四倍频分量的原因与前面定子单位面积磁拉力的情况相同，为磁密高次谐波所致。

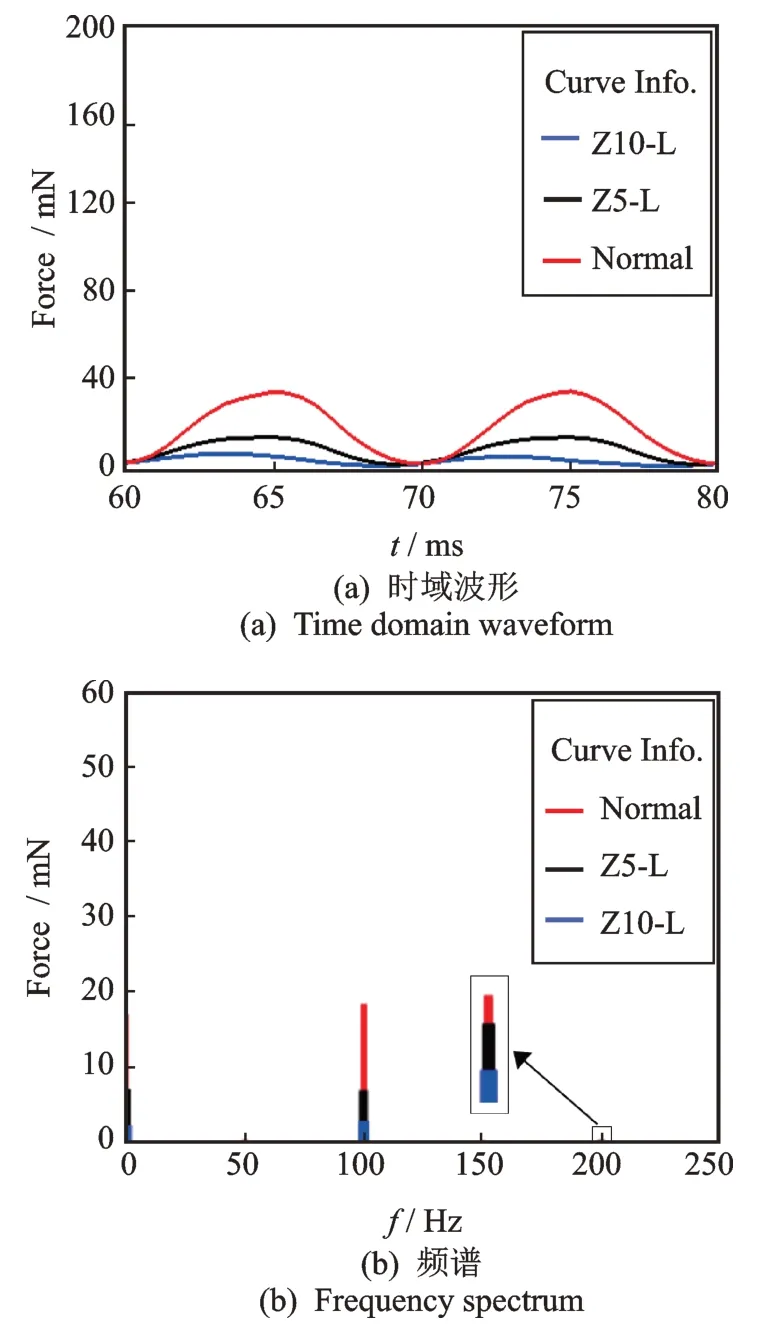
图13 气隙轴向静偏心前后转子抽空侧的绕组电磁力Fig.13 Electromagnetic force of windings before and after axially static air gap eccentricity at the exhaust end of rotor

由表4 可知，相同偏心程度下不同侧的绕组受力不同；而同侧的绕组在不同的轴向偏心下受力也不同。与正常情况相比，轴向偏心下转子抽空侧绕组电磁力较小，而转子伸出侧的绕组电磁力较大；随着轴向偏心程度的加剧，转子抽空侧的绕组电磁力将减小，而转子伸出侧的绕组电磁力则将增大，这与式（14）所呈现的变化规律一致。

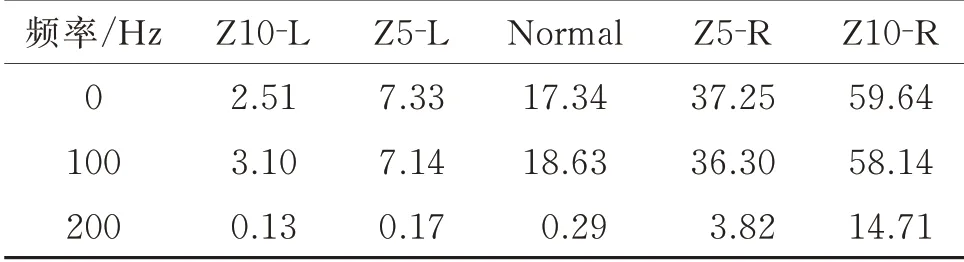
表4 气隙轴向静偏心前后不同侧绕组受力幅值/mNTab.4 Electromagnetic force of windings at different ends under varied axial air-gap eccentricity /mN

2.2 实验验证

2.2.1 实验设置

实验机组与有限元计算的分析对象一致，为CS-5型故障模拟发电机组，如图15（a）所示。该机组的转子通过轴承座固定在基础上保持不动，定子则可通过调节两侧的四枚调节螺钉实现轴向移动，从而模拟轴向静偏心故障，如图15（b）所示。轴向偏移量通过两侧的千分表来进行控制。

实验过程中发电机励磁电流、外接负载均与仿真一致。在定子铁芯轴向与径向分别安装PCB 加速度传感器，分别测取定子轴向和径向振动，如图15（c）所示；同时在定子绕组端部安装PCB 加速度传感器，测量绕组振动，如图15（d）所示。

图15 CS-5 型故障模拟发电机实验设置Fig.15 Experimental setup on CS-5 prototype generator

2.2.2 定子振动响应结果分析

气隙轴向偏心前后的定子径向振动结果如图16 与表5所示。

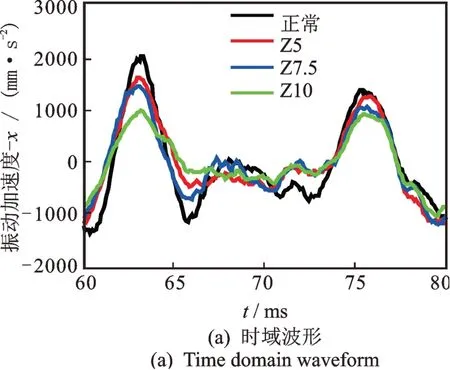
图16 轴向静偏心前后径向振动加速度Fig.16 Radial acceleration of stator before & after axial eccentricity

图16 频谱中的基频成分是转子振动经基础传递至定子的，除基频外主要振动成分为二倍频和四倍频，与仿真分析一致。此外，由于是通过加速度参量来反映振动大小，加速度是位移的二次导数，其直流成分经二次求导后为零，因此在0 Hz 处直流成分为零。结合图16 与表5 可看出，随着轴向静偏心程度的加剧，定子径向振动的时域波形幅值、二倍频与四倍频幅值均减小，这一结果与图11 和表2 的激励数据，以及式（6）的定性结论相一致。

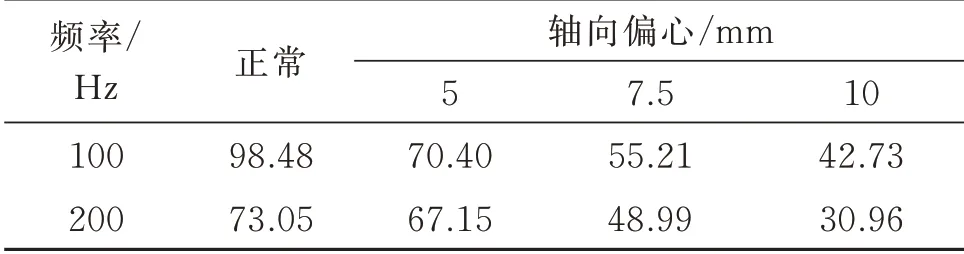
表5 轴向静偏心前后定子径向振动加速度幅值/（mm·s-2）Tab.5 Radial acceleration amplitudes of stator before &after axial eccentricity/（mm·s-2）

轴向偏心前后的定子轴向振动结果如图17 和表6所示。理论上，正常情况下发电机定子轴向不平衡磁拉力为零，应无振动，但由于电机内部的不对称和系统非故障环境因素影响，定子仍会产生以基频及其倍频为主的轴向振动，如图17（b）所示。此外，除偶次频率成分外，所有工况下的频谱在三倍频（150 Hz）处幅值突出，但在理论分析和有限元仿真中轴向不平衡磁拉力并不包含此频率。经多方查找原因，最终发现轴承座在轴向上的一阶固有频率处于150 Hz 附近，图11 中三倍频处的突出振幅由轴承座振动传递至定子铁芯。

由图17 及表6 可看出，除转子和轴承座传递过来的一倍频和三倍频振动外，二倍频和四倍振动幅值加成较为明显，表明轴向静偏心将主要引发定子产生以二倍频和四倍频为主的轴向振动。随着偏心量增大，二倍频和四倍频的幅值也逐渐增大。与径向振动类似，实验中出现四倍频成分并与式（9）激励成分存在差异的根源仍然为磁密高次谐波，此处不再赘述。图17 中二、四倍频成分的振动增幅趋势与图12 有限元结果一致，和理论解析的定性结论也基本相符。

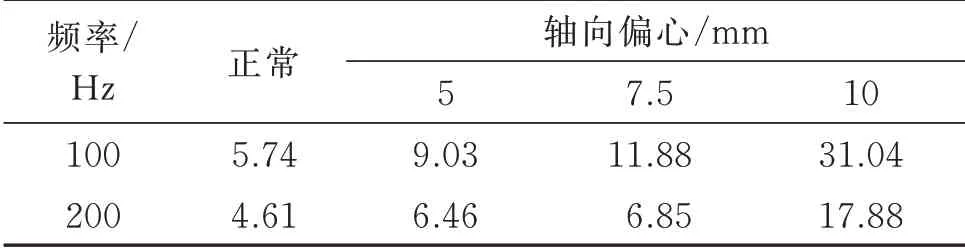
表6 气隙轴向静偏心前后定子轴向振动幅值/（mm·s-2）Tab.6 Axial vibration amplitudes of stator before & after axial eccentricity/（mm·s-2）

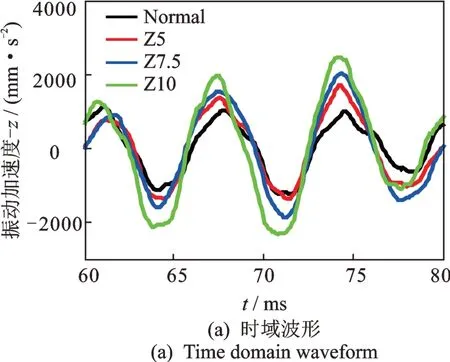
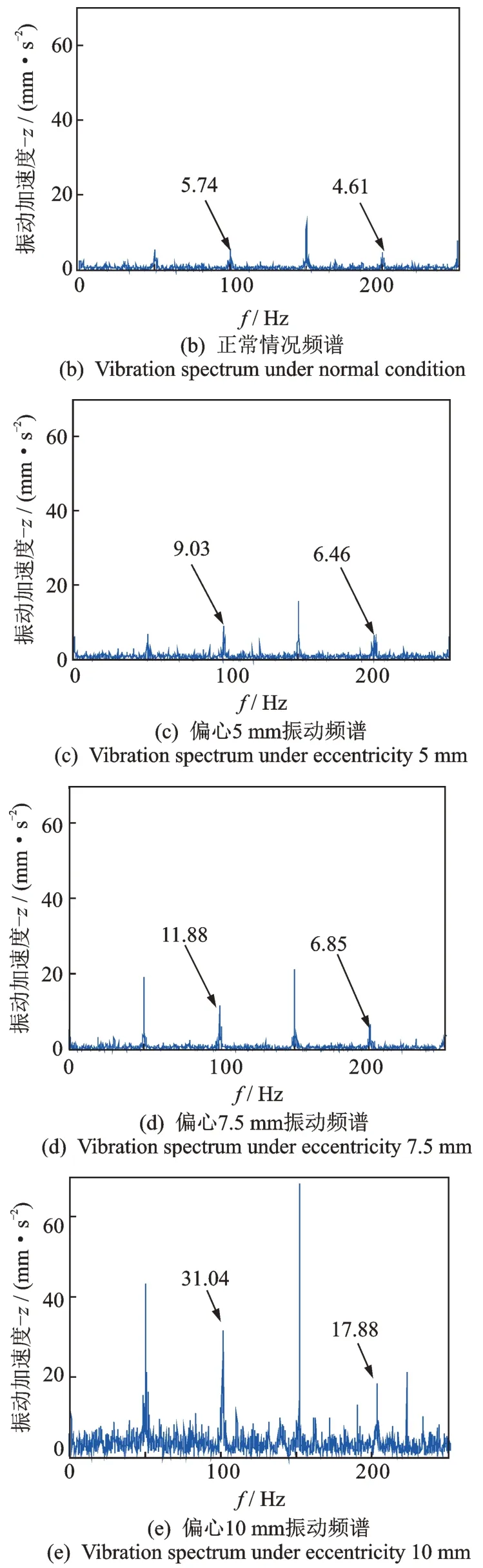
图17 气隙轴向静偏心前后定子轴向振动Fig.17 Axial vibration of stator before & after static axial eccentricity

2.2.3 定子绕组振动响应结果分析

气隙轴向偏心前后的绕组振动如图18，19 及表7所示。由图18,19 可知，定子绕组的振动仍然包含相对突出的二倍频和四倍频成分，尤其是二倍频成分，且这两个成分的幅值在偏心量的变化下均有相对直观的变化，说明轴向偏心将主要对以二倍频为主的偶次倍频振动产生影响；基频和三倍频成分存在的原因与定子振动相同，仍是转子和轴承座振动所传递的二次强迫振动响应。

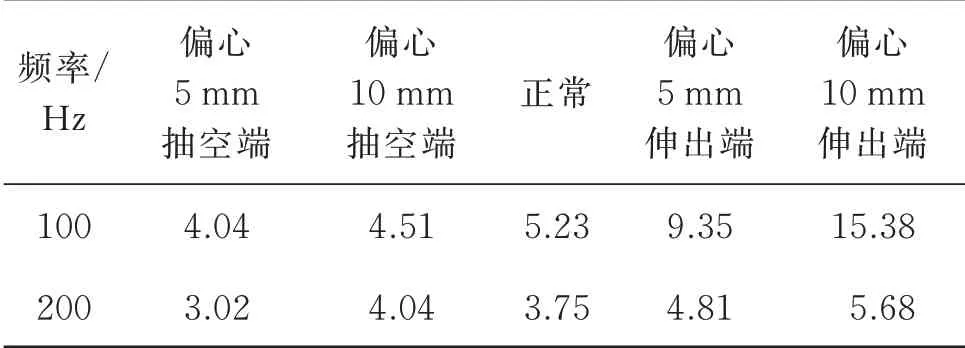
表7 气隙轴向静偏心及正常状态定子绕组振动加速度/（mm·s-2）Tab.7 Acceleration ofstator winding vibration under axially static air gap eccentricity and normalstate/（mm·s-2）

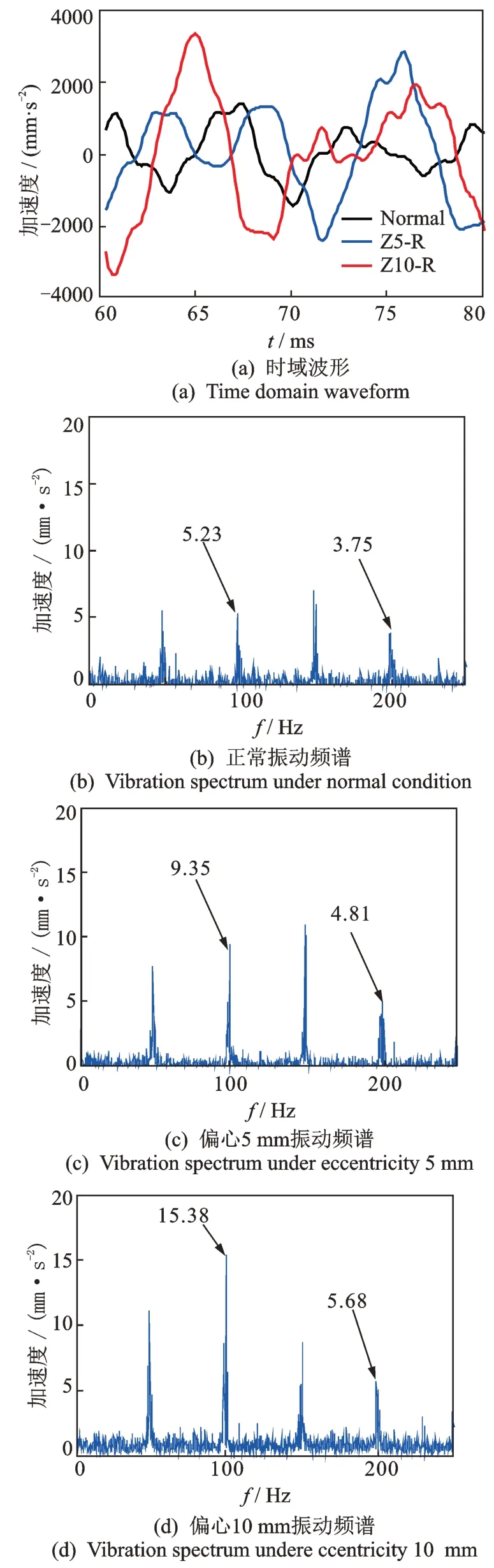
图18 转子伸出端定子绕组振动响应Fig.18 Vibration response of stator winding vibration at the extended end of rotor

与正常状态相比，轴向偏心下转子伸出侧的绕组振动较大，而转子抽空侧的绕组振动较小；随着偏心程度的加剧，转子伸出侧绕组的二、四倍频振动幅值增大，但转子抽空侧绕组的二、四倍频幅值减小。这与理论分析中式（14）、有限元仿真中的图13，14及表4 呈现的变化规律一致。

3 力学响应分析

为进一步分析轴向静偏心前后定子铁芯在磁拉力作用下的铁芯变形以及绕组在电磁力作用下的力学响应，为绕组的磨损监测和维护提供有用信息，在ANSYS Workbench 平台中进行了磁固耦合仿真计算，相应的耦合框图如图20所示，先在Electromagnetic 电磁模块中计算得到铁芯和绕组的力学数据，并将其导入至Transient Structural 瞬态力学分析模块中，得到其变形、应变等力学响应。

图20 ANSYS Workbench 中磁固耦合Fig.20 Magnetic-structural coupling in ANSYS Workbench

3.1 定子铁芯响应分析

计算得到的定子铁芯总体变形情况如图21所示。由图21 可知，不论是正常运行还是气隙轴向静偏心，铁芯总体变形在径向呈对称趋势，长期作用下会使铁芯往椭圆方向拉伸，这与电机学中通过磁场解析得到的结论一致。

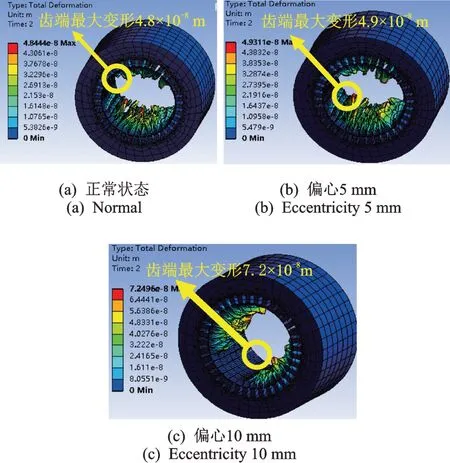
图21 气隙轴向静偏心前后定子铁芯的力学变形Fig.21 Stator deformation before and after axial eccentricity

3.2 定子绕组力学响应分析

正常状态下绕组的力学响应如图22所示。由图22 可知，在电磁力作用下端部绕组鼻端处总体变形最大，渐开线中部也发生了明显的变形。最大应变则发生在端部和直线段的连接部分，这是由于绕组的电磁力对此处的矩最大，所以应变明显，对应的应力也最大，易出现应力疲劳和受铁芯变形挤压而产生磨损。

图22 正常状态下绕组力学响应Fig.22 Mechanical response under normal condition

气隙轴向偏心后的定子绕组力学响应如图23～26所示。由图23～26 可看出，气隙轴向偏心下绕组总体变形的最大处依然位于鼻端，同时渐开线的中部也有明显变形；应变最大处依然出现在端部和直线段的连接部分。从数值方面看，总体变形及应变的峰值从小到大的排序依次为：轴向偏心10 mm 转子抽空侧、轴向偏心5 mm 转子抽空侧、正常状态、轴向偏心5 mm 转子伸出侧、轴向偏心10 mm 转子伸出侧，说明气隙轴向偏心将加剧转子伸出侧绕组的应变和变形，但同时也会减小转子抽空侧绕组的应变和变形，这一结果与式（14）、图13 和图14，图18和图19、表4，7 所呈现的规律一致。

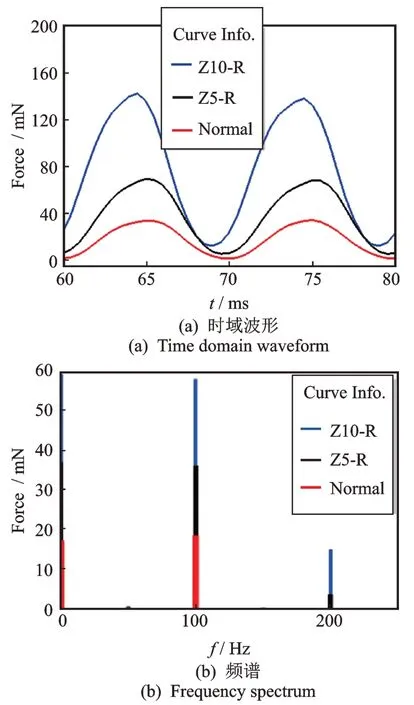
图14 气隙轴向静偏心前后转子伸出侧的绕组电磁力Fig.14 Electromagnetic force ofwindings before and afteraxially static airgap eccentricity atthe extended end ofrotor

图19 转子抽空端定子绕组振动响应Fig.19 Vibration response of stator winding vibration at the exhaust end of rotor

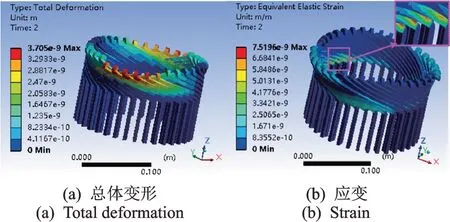
图23 偏心10 mm 状态下转子抽空侧绕组力学响应Fig.23 Mechanical response on the rotor-extraction end under 10 mm axial eccentricity

此外，由图21 可看出定子铁芯的最大变形量均出现在齿槽端部，而由图22～26 可看出定子绕组最大应变位于绕组端部和直线段的连接部分，该部位正好位于铁芯的最大变形位置，在铁芯变形挤压和自身所受应力的综合作用下易产生绝缘损伤。这也很好地解释了大型发电机定子绕组为何经常在直线段与端部连接处发生绝缘损坏的现象，图27 显示了两台实际机组的绕组损坏现场照片，损坏位置均位于直线段与端部的连接部位。

图24 偏心5 mm 状态下转子抽空侧绕组力学响应Fig.24 Mechanical response on the rotor-extraction end under 5 mm axial eccentricity

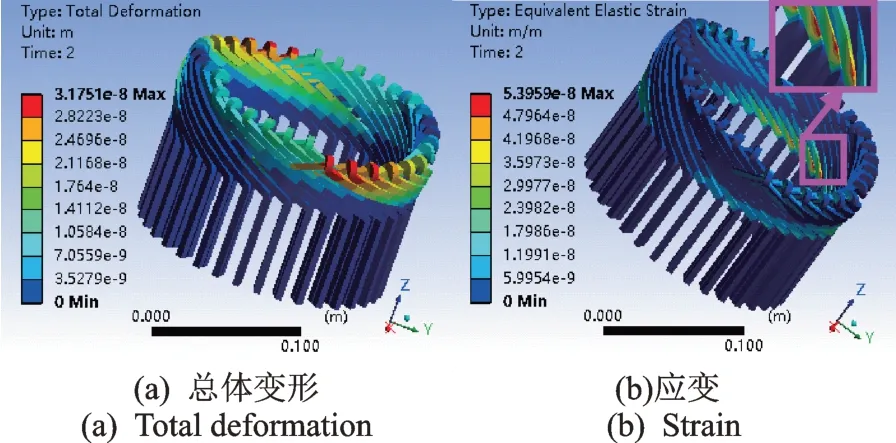
图25 偏心5 mm 状态下转子伸出侧绕组力学响应Fig.25 Mechanical response on the rotor-extension end under 5 mm axial eccentricity

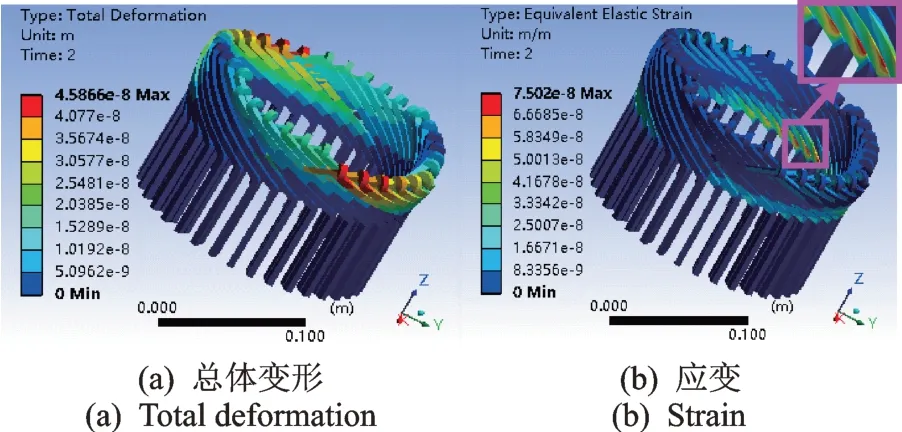
图26 偏心10 mm 状态下转子伸出侧绕组力学响应Fig.26 Mechanical response on the rotor-extension end under 10 mm axial eccentricity

图27 定子绕组直线段与端部连接处绝缘磨损照片Fig.27 Pictures of insulation wear at connection between straight segment and end of stator winding

4 结论

本文对同步发电机气隙轴向静偏心前后的定子-绕组受载及振动进行了分析，结论如下：

（1）提出了定子径向及轴向受载的力学分析模型，推导得到了气隙轴向静偏心前后定子径向及轴向的磁拉力解析表达式，发现轴向静偏心会使定子径向单位面积磁拉力减小，但同时使轴向不平衡磁拉力增大，径向力和轴向力除直流外均以二倍频为主；

（2）建立了定子绕组受载的力学分析模型，推导得到了气隙轴向静偏心前后定子绕组的电磁力表达式，发现轴向静偏心会使转子抽空侧绕组的电磁力减小，但同时会使转子伸出侧绕组的电磁力增大；

（3）以CS-5 型故障模拟发电机为对象进行了有限元仿真计算和实验验证，结果表明在气隙轴向静偏心下，定子径向振动将减小，但轴向振动将增大；转子抽空侧的绕组振动减小，但转子伸出侧的绕组振动增大。定子铁芯在轴、径向力复合作用下齿槽端部的变形最大，此位置正好是绕组直线段与端部的连接位置，同时也是绕组的应变最大位置；绕组该部位易发生磨损，可考虑在制造过程中在该位置涂覆耐磨涂层。

本文工作是对现有气隙偏心成果体系的补充，对于水轮发电机组等易发生气隙轴向偏心的电机绕组安全监测和失效预防具有参考价值和积极意义。