不同类型欧拉屈曲梁非线性吸振器动态特性的影响研究

刘海平，申大山，王 添

（北京科技大学机械工程学院，北京 100083）

引言

非线性动力吸振器（Nonlinear Dynamic Vibration Absorber，NDVA），又可称为非线性吸振器，作为一类典型的非线性振动抑制装置，以其减振频带宽、鲁棒性好、未对主振系的动态响应引入新的谐振峰等优点受到持续广泛的关注，其非线性特征多以非线性刚度形式呈现。研究发现，非线性吸振器能够在较宽频率范围内有效吸收主振系的振动能量，且利用阻尼元件将其耗散［1-3］。

Roberson［4］采用具有线性和立方耦合刚度的非线性吸振器构成的弹簧元件，并将其附加于单自由度结构，通过与线性吸振器相比，在正弦激励下，上述非线性吸振器具有更宽的减振频带。Vakakis［5］将含有本质非线性刚度，可以将振动能量从主振系单向不可逆地传递至耗能元件的非线性吸振器命名为非线性能量阱（Nonlinear Energy Sink，NES）。Zhang 等［6］在非线性能量阱中加入惯容器，通过对比主振系的频响特性和能量传递性能，发现其振动控制效果得到显著提升。Zang 等［7］在非线性吸振器中加入杠杆放大机构，系统传递率得到明显降低。Gendelman 等［8］将多个非线性吸振器串联安装，在保证非线性吸振器总质量不变的条件下，相比单个非线性吸振器呈现更优的抑振效果。上述研究重点是从理论角度讨论非线性吸振器的振动控制效果，仅将非线性吸振器的弹簧元件简化为理想非线性刚度，未考虑非线性吸振器的具体实现形式。

考虑工程实际，非线性吸振器的非线性弹簧元件有多种可行的实现形式，例如：柔性索［9］、弹性薄片梁［10-12］、斜置螺旋弹簧［13］等。其中，弹性薄片梁作为非线性弹簧元件，因其性能稳定，不存在材料蠕变等问题而得到关注与研究。Nayfeh 等［14］对屈曲梁线性模态振动进行了理论分析和实验研究。Winter等［15］设计了由两个叶片组成的欧拉弹簧隔振器，通过调整其弯曲刚度比，可以使隔振系统实现极低的动刚度。充分利用欧拉屈曲梁显著的非线性特征，刘兴天等［10］提出一种具备“高静低动”特征的准零刚度隔振器，理论分析和实验验证均表明其具备极佳的低频减隔振性能。在此基础上，刘兴天等［11］利用上述准零刚度结构，首先提出欧拉屈曲梁非线性吸振器的设想，并初步完成稳态激励条件下的频响特性分析。刘海平等［16］分别考虑稳态载荷和瞬态载荷激励条件下欧拉屈曲梁非线性吸振器的响应特性，较为全面地研究了此类非线性吸振器的振动抑制效果。相比线性吸振器，欧拉屈曲梁非线性吸振器在有效抑制主频振动响应的同时，在其他频段不会引起新的谐振峰，并且有效抑振频带更宽。

实际使用中，针对具备本质非线性特征的非线性吸振器，为了克服重力场影响产生的静态变形，可以采用水平安装或者引入弹性补偿元件有效抵消重力场对非线性吸振器的影响。从上述观点出发，楼京俊等［17］考虑非线性吸振器垂向安装条件下，通过引入弱线性弹簧元件作为弹性支撑，提出改进非线性吸振器的模型。研究表明，相比本质非线性吸振器，含弱线性刚度的非线性吸振器的有效工作频带更宽，抑振效果更好。其他关于安装方式对非线性吸振器抑振性能的影响研究报道较少。综上，经过多年的发展，针对非线性吸振器的理论研究已经获得丰富的成果，为实际应用奠定了很好的基础。但是，从工程实际出发，非线性吸振器的具体实现形式以及可能的影响因素研究尚显不足。

本文在前期研究基础上，以欧拉屈曲梁非线性吸振器为研究对象，考虑实际安装约束分别建立非线性吸振器弹性支撑未接地、弹性支撑接地以及仅弹性支撑中弹簧元件接地三类动力学模型，采用复变量-平均法分别给出上述三类模型的频能方程和频响函数表达式。通过对比研究，确定较优的安装方式，并评估其振动抑制效果。

1 欧拉屈曲梁非线性吸振器建模

仅由欧拉屈曲梁构建的非线性吸振器模型如图1所示。初始状态下，每根欧拉屈曲梁长度为L，设在水平位置时，模型处于平衡状态。由于欧拉屈曲梁含有负刚度和非线性刚度，属于一类典型的非线性吸振器。

图1 欧拉屈曲梁非线性吸振器Fig.1 Schematic of the NVDA with Euler-buckled beams

考虑研究内容的完整性，首先，建立单根欧拉屈曲梁模型如图2所示。初始状态下，单根欧拉屈曲梁中间初始挠度为q0，在轴向载荷P作用下，其轴向末端位移为y。

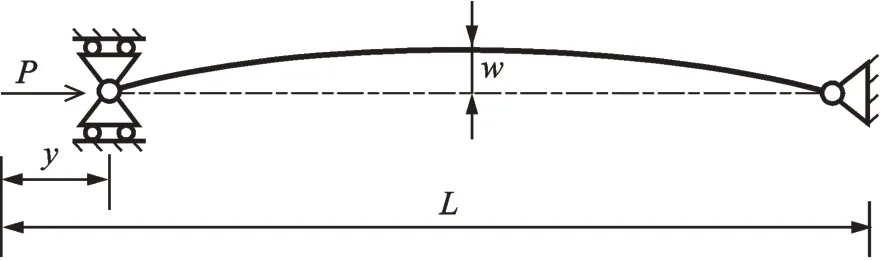
图2 单根欧拉屈曲梁模型Fig.2 Schematic of single Euler-buckled beam model

轴向载荷P与轴向末端位移y之间的关系为：

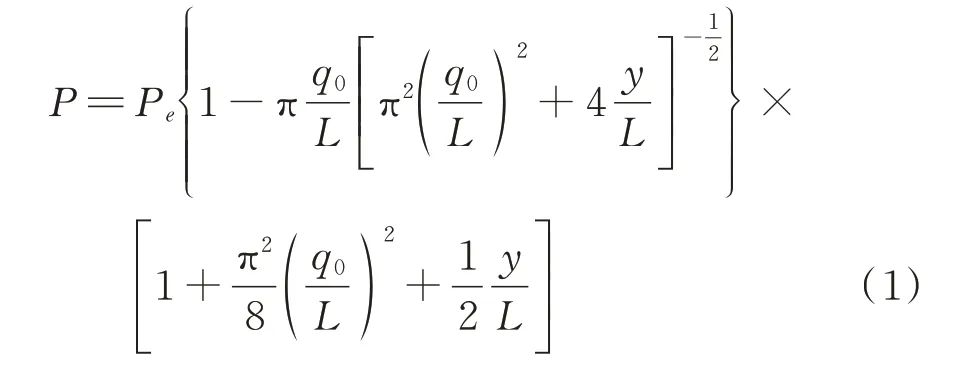
式中Pe=EI(π/L)2为欧拉屈曲梁临界载荷；L，E，I分别为欧拉屈曲梁未变形时的长度、材料弹性模量和梁截面惯性矩。

根据单根欧拉屈曲梁的轴向力-位移关系式（1），可以得到由欧拉屈曲梁构建的非线性吸振器（参见图1）的垂向力-位移关系式。为了简化计算，采用泰勒级数展开可得到力-位移关系的近似表达式［10］：

2 含非线性吸振器耦合动力系统建模

欧拉屈曲梁属于双稳定状态结构，在两个稳定状态之间存在非稳定状态，因此，需要增加辅助弹性支撑保证非线性吸振器的工作稳定性并补偿重力引起的位移。为了系统研究弹性支撑及安装方式对非线性吸振器有效性的影响。本部分分别提出并建立三类非线性吸振器模型：（1）弹性支撑未接地；（2）弹性支撑接地；（3）仅弹簧元件接地，如图3所示。由图可见，M为主振系惯性质量，K为主振系弹性系数，c1为主振系阻尼系数；m为非线性吸振器的惯性质量，k为弹性支撑的弹性系数，c2为弹性支撑的阻尼系数；f=f0cos(ωt)为外部激励力。

根据牛顿第二定理，分别给出图3 不同耦合动力系统的运动微分方程：

图3 不同安装方式的非线性吸振器耦合系统模型Fig.3 Schematic of the NDVA coupling system models with different installation methods

模型1：弹性支撑未接地：

模型2：弹性支撑接地：

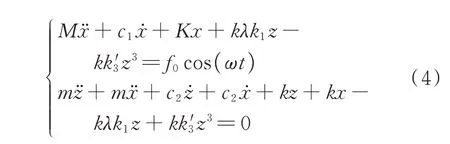
模型3：仅弹簧元件接地：

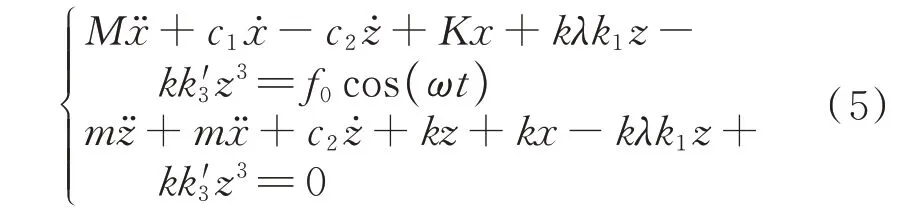
为了便于分析，引入无量纲化参数：

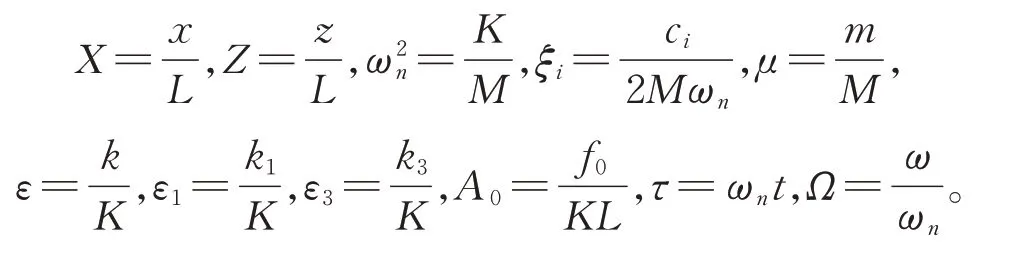
通过无量纲化处理，公式（3）～（5）对应不同模型的运动微分方程变换为：

模型1：弹性支撑未接地：

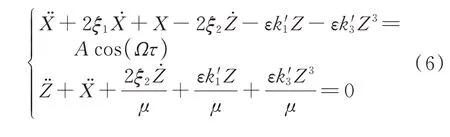
模型2：弹性支撑接地：

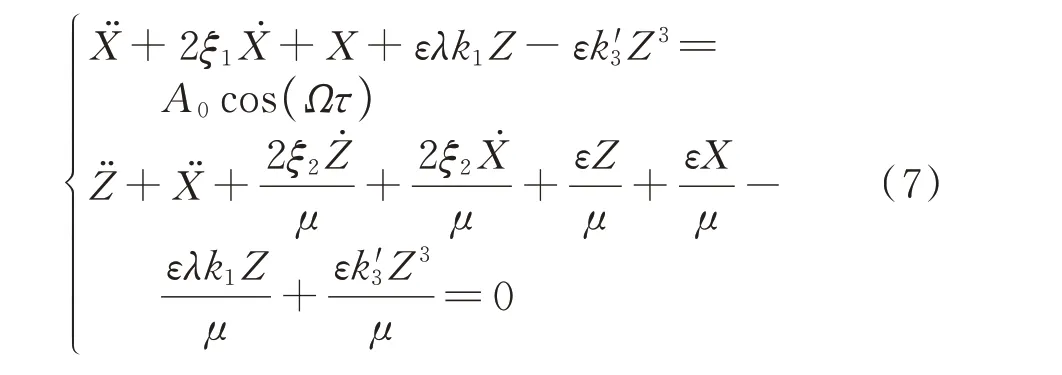
模型3：仅弹簧元件接地：

3 稳态解析解

3.1 频率能量方程

非线性吸振器对线性主振系的振动控制主要通过耦合系统发生内共振的方式实现。上述内共振形式共分为主共振、亚谐共振和拍振三种类型，且各类型共振形式随着系统能量水平变化而被激发。其中，最常见且控制效果最明显的为主共振。目前，频能图作为有效的分析工具被广泛应用于研究非线性吸振器的振动控制效果。非线性振动系统的频能图在一定程度上可以看作是线性振动系统中的幅频特性曲线在非线性振动系统中的一个拓展，它反映了非线性系统内各阶非线性模态之间的耦合作用，同时也反映了非线性系统的各种内共振分布规律［18-19］。

本部分使用复变量-平均法［20-22］，重点研究非线性吸振器与主振系之间发生1∶1主共振时的动态特性。

首先，定义复变量：

频能图仅适用于保守系统，故需将方程中阻尼项和外部激励项忽略掉；然后，引入复变量。通过化简，可得主振系惯性质量的振幅和主振系惯性质量与非线性吸振器间的相对运动幅值，分别采用A和B表示。对应图3 给出不同耦合动力系统模型的响应幅值，分别得到：

模型1：弹性支撑未接地：

模型2：弹性支撑接地：

模型3：仅弹簧元件接地，该工况与模型2 对应频能曲线的表达式相同，故不再赘述。保守系统的能量与频率之间的关系如下式所示：

3.2 频响方程

使用复变量-平均法求解频响函数［23-28］，以弹性支撑未接地模型为例，将第3.1 节定义的复变量引入式（3），得到：

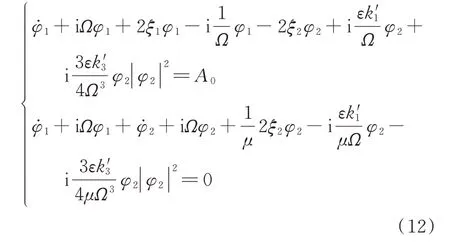
引入变量φ1=a1+ib1，φ2=a2+ib2，其中a1，b1，a2，b2均为时间t的函数。分离实部和虚部，求出a1，b1，a2，b2后代入式（12）可求出频响方程［29-31］：

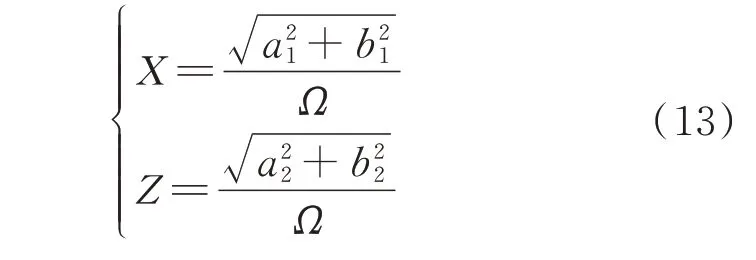
采用其他安装方式时的非线性吸振器耦合系统动力学模型相应的频响方程详见文后附录。为了验证解析解的正确性，采用四阶龙格-库塔法计算得到的数值解进行对比验证，如图4所示。由图可见，计算结果一致性较好，满足精度要求。

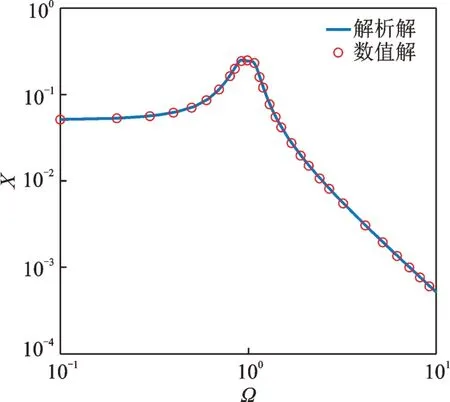
图4 解析解与数值解对比Fig.4 Comparison of analytical and numerical solutions

4 动力学特性及抑振效果

本文研究重点在于分析不同安装方式对欧拉屈曲梁非线性吸振器有效性的影响，故具体设计参数参考文献［16-17］，如表1所示。需要说明，文献中所列参数均为优化后结果，故本论文不涉及最优化设计相关工作。结合第3 节已给出不同耦合系统频率能量方程和频响函数，对上述三种不同安装方式的欧拉屈曲梁非线性吸振器的动态响应特性及抑振效果展开讨论。

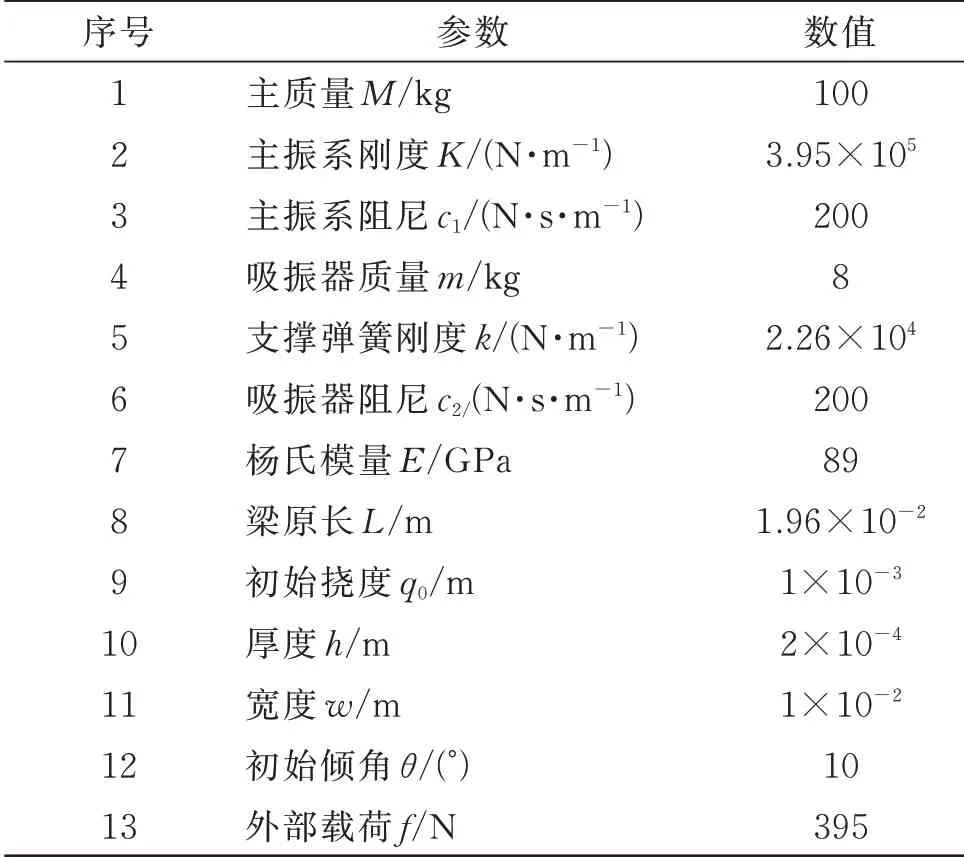
表1 设计参数值Tab.1 Design parameter values

4.1 频能图

图5 给出不同安装方式非线性吸振器耦合系统对应的频能图。由图可见，在定义的频率范围内对系统模型进行遍历计算，可以得到两条不同的脊线。考虑非线性吸振器稳定性，引入弹性支撑导致非线性吸振器的刚度出现线性项，对应耦合系统频能曲线呈现两个互不相交的分支。其中，上分支对应一阶非线性模态，代表主振系与非线性吸振器之间的反向运动；下分支对应二阶非线性模态，代表主振系与非线性吸振器之间的同向运动。可以看出，一阶非线性模态的振动频率出现下饱和现象，随着能量的减小，振动频率收敛于固定值。对比发现，受安装方式影响，弹性支撑未接地情况频率变化范围较宽，弹性支撑接地情况频率变化范围较窄。

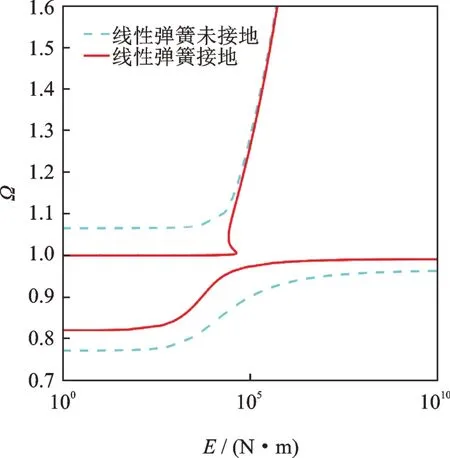
图5 不同模型对应的频能图Fig.5 Frequency-energy plots for different models

4.2 频响曲线

本部分给出不同安装方式非线性吸振器对应耦合系统主振系的频响曲线，进而重点讨论安装方式变化对其抑振效果的影响。

图6 给出欧拉屈曲梁非线性吸振器采用不同安装方式对应的主振系频响曲线。通过安装弹性支撑，欧拉屈曲梁非线性吸振器工作状态保持稳定，故主振系频响曲线未出现跳跃现象等典型的非稳态响应特征。其中，弹性支撑未接地时，欧拉屈曲梁非线性吸振器抑振效果最好。此外，引入弹性支撑的欧拉屈曲梁非线性吸振器不仅可以有效抑制主振系的频响幅值；而且，未在其他频点引入新的谐振峰。这也是此类非线性吸振器的突出优势。

图6 不同模型对应的主振系频响曲线Fig.6 Frequency response curves of the main vibrational system for different models

根据上述分析结果，后面内容重点针对弹性支撑未接地对应的欧拉屈曲梁非线性吸振器动力耦合系统展开讨论。

4.3 与线性吸振器对比

本部分重点讨论安装传统线性吸振器和欧拉屈曲梁非线性吸振器对主振系振动响应的抑制效果。根据第4.2 节计算结果，弹性支撑未接地时，欧拉屈曲梁非线性吸振器抑振效果最好。本部分选择该方案作为研究对象。

图7 给出不同类型吸振器对应的主振系频响曲线。可见，两类吸振器均可在主振系谐振频率实现有效抑制响应峰值的目标。但是，传统线性吸振器在原系统谐振频率两侧引入新的谐振峰；欧拉屈曲梁非线性吸振器除了可以有效抑制谐振频率主振系的响应峰值，在其他频段则未产生任何负面影响。

图7 不同类型吸振器对应的频响曲线Fig.7 Frequency response curves for different types of dynamic vibration absorbers

4.4 时域响应

根据第4.3 节研究内容，欧拉屈曲梁非线性吸振器可以显著抑制主振系谐振峰值，并且在谐振频率附近未引入新共振峰，拓宽了工作频带；而且，在其他频段未产生负面影响，即未在低频段引入新的谐振峰，在高频段振动响应未被放大。

实际中，环境激励呈现多频宽频特征，为了全面了解欧拉屈曲梁非线性吸振器的抑振效果，以下重点在时间域讨论其受多频稳态激励的振动控制效果。

具体计算过程：针对安装不同类型非线性吸振器耦合系统的运动微分方程，采用四阶龙格-库塔法进行数值计算，得到各部分的时域响应位移曲线。

假设系统所受外激励F=∑cos（ωt），ω=21，32，42，52，63，71，84 rad/s 为多频力激励对应圆频率。计算得到在时间域多频力激励条件下安装不同类型非线性吸振器耦合系统各部分位移响应曲线如图8所示。由图可见，非线性吸振器振动抑制效果优于线性吸振器。

图8 时域位移曲线Fig.8 Displacement curves in time domain

5 影响因素分析

相比传统线性吸振器，欧拉屈曲梁非线性吸振器设计参数众多，其中，初始挠度q0、长度L以及斜置倾角θ为新增设计变量，故本部分重点针对上述三个新增参数对安装欧拉屈曲梁非线性吸振器耦合系统动态响应的影响进行分析。

5.1 初始挠度q0的影响

其他参数保持不变（参见表1），初始挠度q0在［1×10-4m，3.5×10-3m］区间内变化，得到主振系幅频特性云图如图9所示。q0在7×10-4～2.1×10-3m 范围内变化时，主振系谐振峰对应频率比位于0.90～0.95 之间，且q0约为1.3×10-3m 时，主振系频响峰值最大。当q0小于7×10-4m 或大于2.1×10-3m 时，主振系谐振峰会出现在频率比1～1.05 之间。此外，初始挠度q0在［5×10-4m，7×10-4m］和［2.1×10-3m，2.3×10-3m］区间取值，主振系谐振峰存在较小值，即初始挠度q0存在最优值。

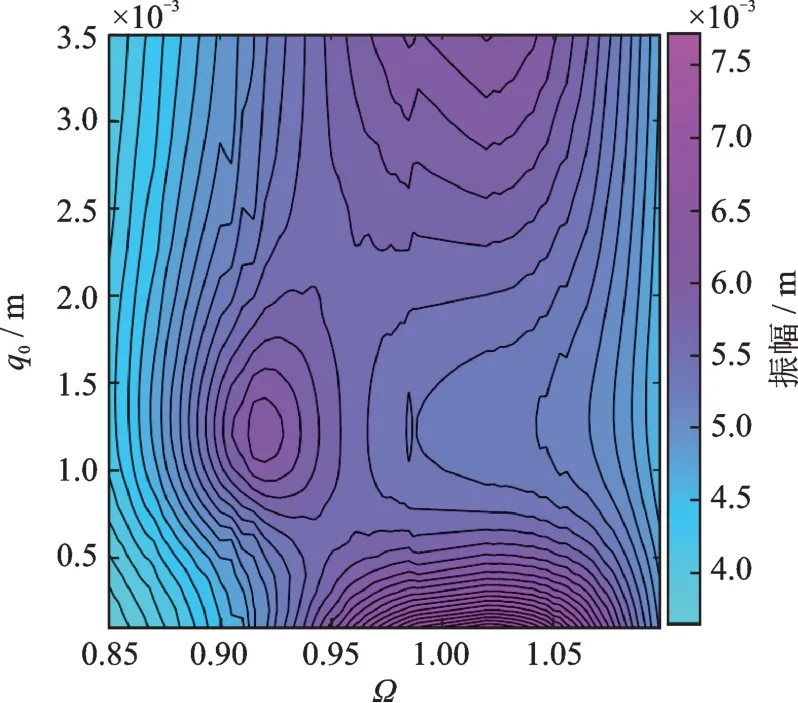
图9 不同q0值对应主振系频响曲线Fig.9 Frequency response curves of the main vibrational system for different q0

5.2 长度L 的影响

其他参数保持不变（参见表1），仅在区间［0.01 m，0.06 m］内改变L值，得到主振系幅频特性云图如图10所示。当L在0.019～0.06 m 范围内变化时，在频率比1～1.05 内出现共振峰，且随L的减小共振峰呈现“先减小后增大”的变化趋势；而且，当L约为0.019 m 时，主振系频响幅值最小；如果L继续减小，共振峰频率比移向0.92～0.96 区间；随着L继续减小，主振系频响幅值急剧上升。对比可见，长度L的最优值位于区间［0.019 m，0.022 m］，相应系统谐振峰值最小。

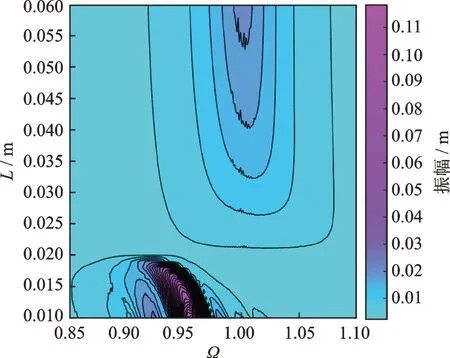
图10 不同L 值对应主振系频响曲线Fig.10 Frequency response curves of the main vibrational system for different L

5.3 斜置倾角θ 的影响

其他参数保持不变（参见表1），当斜置倾角θ在区间［5°，25°］变化，主振系幅频特性云图如图11所示。当斜置倾角大于10°时，主振系谐振峰频率比位于1～1.05 区间；随斜置倾角的减小而呈现“先减小后增大”的变化趋势；当斜置倾角约为10°时，主振系频响幅值最小；随着斜置倾角继续减小，主振系谐振峰值急剧增大且向低频发生移动。对比可见，斜置倾角也存在最优值位于区间［10°，14°］，对应主振系谐振峰值最小。

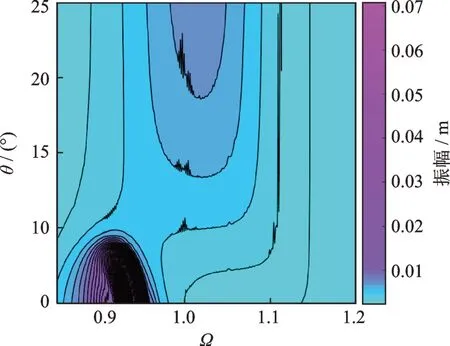
图11 不同θ 值对应主振系频响曲线Fig.11 Frequency response curve of the main vibrational system for different θ

6 总 结

为了研究基于欧拉屈曲梁非线性吸振器安装方式对其振动抑制效果的影响，本文分别提出弹性支撑未接地、弹性支撑接地和仅弹簧元件接地三类耦合系统模型。采用复变量-平均法，获得不同模型对应频响函数，进而得到系统的频能方程。通过与传统线性吸振器对比，以及主要设计参数的影响分析，综合分析并评价欧拉屈曲梁非线性吸振器振动抑制效果。根据计算结果，具体得出以下结论：

（1）在三类非线性吸振器模型中，采用弹性支撑未接地方式安装的欧拉屈曲梁非线性吸振器的振动抑制效果最好；

（2）相比于传统线性吸振器，欧拉屈曲梁非线性吸振器不仅可以有效抑制主振系的谐振峰值，且对其他频段的振动响应未产生负面影响；

（3）对比主振系频响幅值，欧拉屈曲梁非线性吸振器的主要设计参数初始挠度q0，长度L和斜置倾角θ均存在最优值。

附 录：

模型1：弹性支撑未接地：

模型2：弹性支撑接地：

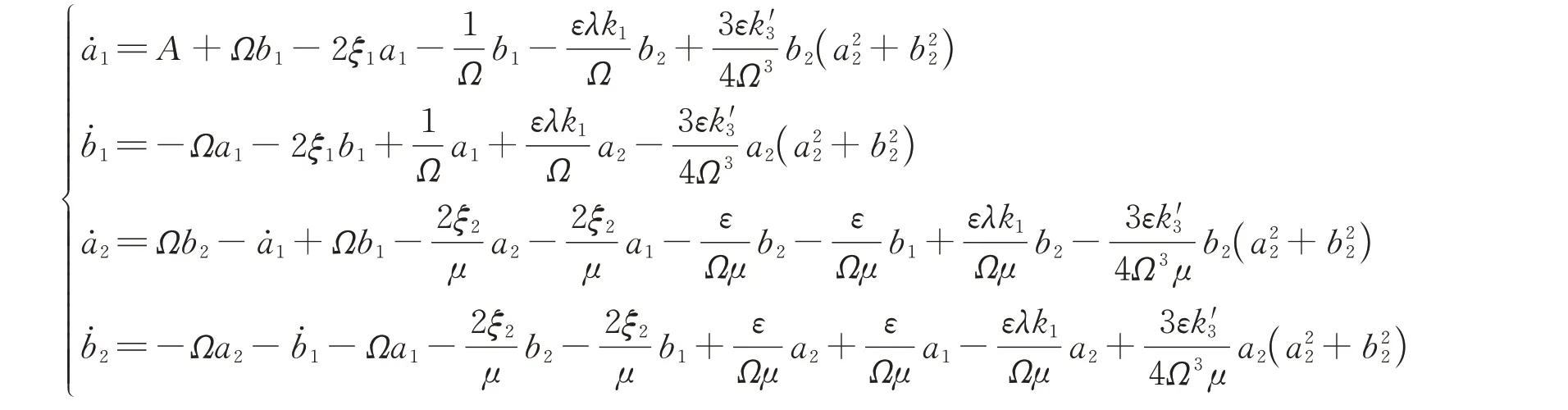
模型3：仅弹簧元件接地：