采用PCA/D-S方法及FUKL融合算法的主轴系统弱故障动态判别与辨识

2022-07-26王伟平

振动工程学报 2022年3期

王伟平，王琦，2，于洋，李宁

（1.沈阳工业大学信息科学与工程学院，辽宁沈阳 110870；2.辽宁工业大学，辽宁锦州 121001；3.大连理工大学机械工程学院，辽宁大连 116024）

引言

智能机床作为复杂、精密、智能化的加工装备，影响其加工的故障因素有多种。对于刀具、装卡等外在影响因素通常可以较为直观地判定，但对于机内主要部件的弱故障（即故障损伤特征不明显，常用的故障诊断方法难以准确判别）所产生的动态刚度不足因素，往往难以辨识、追溯故障源。

对于机床及其组件的刚度及加工性能的研究较多。王磊等［1］通过研究机床结合面刚度矩阵，提出了机床固定结合面形状的拓扑设计方法。赵兴玉等［2］通过提出并联机床整机动力学建模方法研究了动刚度预估与设计的理论。Chen 等［3］通过研究滚珠丝杠副的动刚度，提出了无传感器刚度估计方法。姜晓飞等［4］通过有限元仿真分析研究了机床在不同频段下的动态特性。Kondo 等［5］从材料和热位移的角度研究了主轴动刚度性能。Kono 等［6］从薄壁件加工的角度研究了切削中影响振动的动刚度问题。Živkovic′等［7］通过建立三维有限元热模型研究了主轴系统的加工动态性能的提升。Su 等［8］利用激励模型分析了动刚度对加工零件表面质量的影响。

上述对机床刚度的研究主要从机械固有特性的角度进行理论、仿真、热位移研究，而从负载加工角度，对机床动刚度不足引起的加工精度下降等切削故障问题的相关研究很少。实际应用中，对出现加工问题的故障机床，在排除多种外在故障因素后，如何深入研究其表现的动刚度不足特征，并能量化建模分析特征，成为解决该类问题的有益探索。

对于机床这类由多部件系统构成的复杂非线性组合体，进行其动刚度研究不仅要关注整体，同时更要关注主要部件的变化特征。

在机床的众多部件系统中，主轴系统是机床最重要的动力、承载部件，对其故障的辨识以及故障界定是实际中判定机床故障的重要环节。Wang 等［9］利用粒子群优化和BP 神经网络研究了主轴热误差引起的机床加工精度问题。Yue 等［10］使用模糊聚类和灰度相关算法进行了关于减少主轴热误差载荷对加工精度影响的研究。Chen 等［11］研究通过转子摆动轴承刚度来辨识主轴系统刚度。Nam 等［12］通过建立电主轴鲁棒控制器研究了电主轴系统的扰动故障。

上述对主轴系统的研究集中在热误差、零件刚度、干扰等方面。机床是一种加工工具，对故障主轴系统在负载加工状态下的动刚度研究更具实际意义。

对故障机床动刚度的研究，应以切削状态为研究背景，相关故障诊断与建模研究应以特征分析和机理研究为途径。从故障机理角度进行故障诊断的研究较多。郭磊等［13］基于小波核主元特征约简方法研究了转子故障模式。Hwang 等［14］基于PCA 进行了主风机故障特征方面的研究。李元等［15］基于PCA 的改进方法进行了基于多模态数据全信息概率的故障研究。Cheng 等［16］基于改进的D-S 证据理论进行了风力机齿轮箱故障的智能化诊断。Qiu等［17］将D-S 证据理论应用于风电场智能化管理以实现报警分析。

综上，为解决机床装备及其主轴系统等主要固有部件因其内在弱故障所引起的动态刚度不足，进而产生加工问题判别和溯源难度大的问题，本文以含颤振故障的机床为研究对象，以故障溯源为主线，在工程实际中对引起颤振故障相关因素逐一排查仍未解决问题的前提下，从机床自身主要部件刚度（含动刚度、静刚度）角度，以动刚度不足为判别内容，通过分析故障特点，研究算法特点，提出了基于粗、精维度的故障判别与辨识算法，实现了对于故障机床及其主轴系统内在组件弱故障所产生的动刚度不足问题的判别与辨识溯源的方法研究。

1 机床动刚度不足相关故障的特点及研究难点

1.1 相关故障的特点

机床的动刚度是指机床面对交变载荷作用时抵抗变形的能力，是评估机床抵抗振动变形的主要特征。机床在非共振频率区间内工作时，动刚度越大，则机床在动态作用力的影响下振动幅度越小，抵抗振动的能力越强，加工特性越好。

机床的静刚度，是在静载荷作用下抵抗变形的能力，由其内在零部件的接触刚度决定。工程实际中，如构成机床主要部件的零部件因弱故障而产生静刚度异常，则机床在加工中会表现出动刚度异常。

实际中，机床因自身动刚度不足会在加工零件表面产生颤振振纹（如图1（b），图1（a）为与之对比的无振纹零件）。颤振振纹是一类较常见但成因复杂的加工问题。其成因包含机外因素，如工件材质、切削参数、切削轨迹、装卡、刀具因素等。此外，机床自身的机内因素是另一个主要方向，如结构件明显损伤、主轴系统动刚度不足、刀具进给系统动刚度不足、床身动刚度不足、主电机动态特征异常等。工程实际中，机外因素一般通过同类更换能够直接确定，而机内因素一般通过对明显损伤进行故障诊断及拆解机床判定。

图1 加工零件对比Fig.1 Comparison of machined parts

1.2 相关故障研究的难点

机床的主轴系统、刀具进给系统、床身组件等在加工中受力后，这些部件中原有静刚度薄弱的环节会出现不同程度的刚度不足特征加剧，表现为局部内在接触面的微观变形，运行的轻微振动、共振，甚至运行抖动。实际中，这些可能的故障因素都会带来颤振振纹。但这些静刚度不足的弱特征故障通常难以在整机装配完整后的非加工空载条件下被直接检出，往往通过某些加工过程中的动刚度不足问题在加工件表面被反映出来。出现该类故障后，在排除机外因素及对机内故障诊断未发现明显故障特征的条件下，缺乏有效的算法和数据分析手段再具体定位参与加工的哪个主要部件出现问题。在实际中，靠逐一拆卸更换主轴系统、刀具进给轴系统以及调整床身支撑点的稳定性等方法尝试解决，效果往往不明显或无法溯源到故障的本质，这一方面体现出该类问题解决的难度，同时另一方面也对相关研究提出了需求。

2 数据处理及算法建模

2.1 整体-局部的研究架构

基于上述分析，本文主要针对机床装备及其主要部件系统因其内在组件弱故障所引起的动刚度不足，进而产生的加工件颤振振纹问题展开溯源算法研究，提出了由PCA/D-S 组成的故障特征部件粗定位判别算法研究维度，及由FUKL 融合算法（FU：模糊集；KL：相对熵）构成的细粒度辨识算法研究维度所共同组成的整体-局部研究架构，如图2所示。

2.2 特征数据的选取

由图2 可知，根据从主要部件层面溯源故障机床颤振振纹故障的研究需要，结合动刚度判别研究中对于时频域特征提取的需要，在粗定位维度，选取反映振动波形变化的时频特征量进行研究，并以这些特征量的数值变化幅度均值特征作为判定特征。

图2 整体-局部研究架构Fig.2 Overall-local research framework

在细粒度维度，对主轴系统，根据其特点，从周期性特征与发散性特征等区分角度选取幅值最大的前20 个点对应的变化特点作为特征量展开研究。

2.2.1 振动波形的时域特征选取

在时域范围内，通过对振动传感器的检测数据分析比较，本文选用振动波形的时域特征参数包括：时域波形的最大值、最小值、峰差值、绝对平均值、方差、标准差、峭度、偏度、均方根、均方根因子、峰值因子、脉冲因子，共12 项时域波形特征。

2.2.2 振动波形的频域特征选取

加工切削振动波形包含大量的高频特征，频域频谱特征是分析高频特征的有效手段。本文采用FFT 算法（快速傅里叶变换）进行时-频域变换。

频谱能够精确地反映每种工况下机床部件对应位置及方向的振动特征。频谱幅值反映的是不同频率点的振动强度，其数值的大小可以反映对应机械结构在受外力激励下的响应程度，即动态刚度的实际情况。并且，同一方向同一工况下，相邻切削条件的频谱幅值的整体均值具有明确、各异的变化特征。其在相邻切削条件下的变化幅度可以反映动态刚度的变化。据此，结合研究中实际采集到的相关频谱数据的变化特点，本文选取频谱振幅中位数、频谱振幅平均值、频谱幅值最大值几个能够体现频谱幅值的中位特征、平均特征、最大特征的典型特征量作为特征值。同时将体现单位频带内信号功率平均值特征的功率谱平均值也作为特征量，力求从频域角度全面提取输入的振动信号数据的振动强弱特征，尽可能多地获取动刚度的变化趋势特征。

2.3 算法相关理论基础

2.3.1 PCA 主成分分析的特点

PCA 主成分分析，是一种数据降维算法。其原理是将原数据的m维高维特征映射成n维低维特征（m＞n），新产生的具有正交特点的n维特征即为主成分。最初3 维特征含有原数据99% 以上的可变性。

2.3.2 D-S 证据理论的核心

D-S 证据理论是一种人工智能领域的数据推理理论，其理论核心如下：

（1）Dempster 识别架构：

这里，mi是识别架构Ω的某一随机值。识别架构Ω的所有子集，通常标识为2Ω，则有：

如式（1），识别架构Ω的任一子集B能够被理解为问题的答案。

（2）信任配比函数：

识别架构Ω上的基本信任配比函数n，被定义为2Ω到［0，1］的某个映射，其满足：

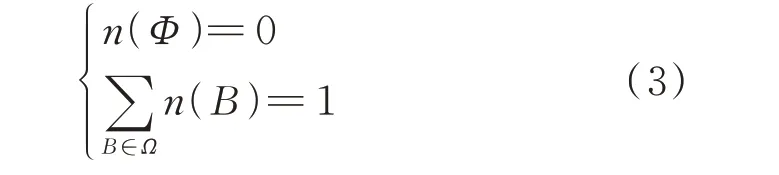
n(B)可以表述证据信息对B的信任程度，即基本的信任配比数值。空集为零，余下的全部B的信任配比数值累加为1。当n(B)＞0，B被定义为焦元。

（3）合成标准：

如识别架构Ω存在证据E1和E2，对应的信任配比为n1和n2，Ci和Dj为焦元，可得D-S 的合成标准：

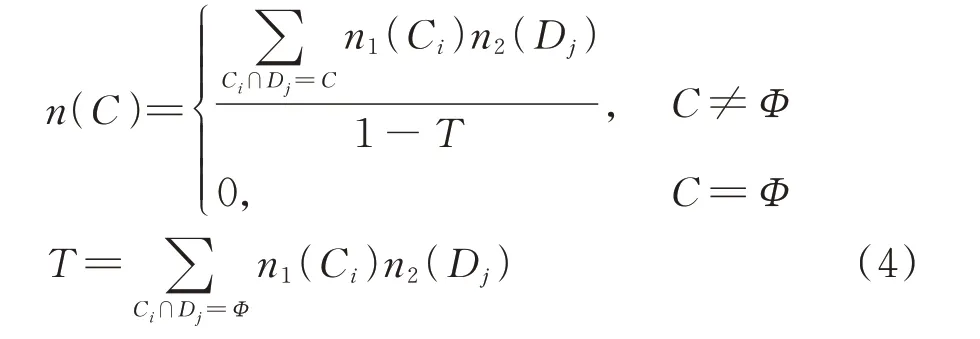
式（4）中T为冲击系数，越大表明证据间冲击越大。

2.3.3 模糊集理论的含义

模糊理论（Fuzzy Theory）涉及模糊集理论和隶属度函数理论。模糊集是一种数据信息分析方法。其理论含义为：设X是元素集，x是X的一个元素分类，即X=｛x｝，则将X命名为论域。X内的模糊子集C可依赖于隶属度函数C(x)来定义。C(x)的取值范围为［0，1］。

当C(x)=1 时，x被认为完全隶属于C；

当C(x)=0 时，x被认为不属于C；

当0＜C(x)＜1 时，x被认为部分隶属于C。

所以，可以认为模糊集合的实质是定义了一类关于x及与其配合的隶属度函数所构造的序列。即：

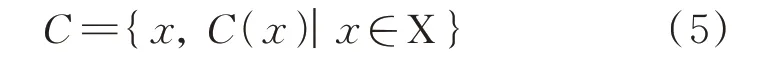
2.3.4 相对熵理论的特点

相对熵又称KL 散度，用来衡量由随机变量x构成的2 组独立分布特征P（x）及Q（x）之间的差别。如果用P（x）表示理想的概率分布，用Q（x）表示实际概率分布，当Q（x）越接近P（x），说明Q（x）与P（x）的差异越小。这种接近程度用相对熵标准公式来表示：

式中n为随机事件的全部概率，DKL的结果越小，说明Q（x）与P（x）的概率分布越接近。

2.4 本文提出的算法模型

2.4.1 PCA/D-S 算法模型的提出

为研究颤振故障机床各主要部件的动刚度变化特征，实现粗定位出动刚度薄弱环节，即针对故障机床在排除其他因素后从机床主要部件动刚度角度溯源故障部件，本文针对粗定位维度的研究，提出了PCA/D-S 算法模型（如图3所示）。

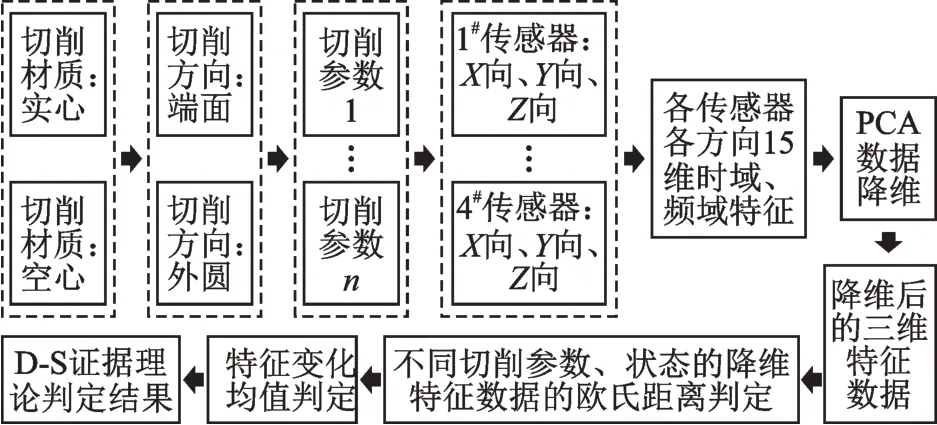
图3 PCA/D-S 算法结构Fig.3 The structure of PCA/D-S algorithm

图3 中使用欧氏距离作为PCA 降维数据的变化特征衡量，其意义在于衡量经PCA 降维聚类后的三维数据（放在由3 个PCA 降维维度构成的三维空间内）在数值层面变化量的大小程度。以空间三维欧式距离表示这种变化程度，距离的远、近表示变化程度的大、小。另在研究中，使用小波包软阈值降噪对研究数据进行了滤波降噪预处理。

2.4.2 FUKL 融合算法模型的提出

在实现对机床整机动刚度薄弱部件判别研究后，可展开对主要功能部件动刚度不足相关故障的细粒度辨识研究。机床的主轴系统作为机床参与加工的核心部件，对其负载加工状态下动刚度不足相关故障的进一步辨识具有重要意义。

在研究模糊集数据信息分析优势与相对熵差异分布比较优势的基础上，本文提出了FUKL 融合算法模型（如图4所示），有效解决了负载加工态下主轴系统动刚度不足相关故障的辨识问题。算法原理如下：

（1）如图4所示，A，D分别是论域X指向［0，1］值域的映射，被定义为模糊子集。设定x的元素以二维向量（F，R）表示，则A，D隶属度判别函数如下：

式（7）和（8）中的f0为主轴的回转周期频率。F为特征点的频率值。R为特征点对应的幅度值。i为i-1 在单一变量变化下的邻近下一状态。Ri＞Ri-1表示临近状态下幅度值增强。FRi为当幅度为Ri时的频率值，FRi-1同理。KLPA表示TOP20 中特征点的轴向隶属度概率，即为依据下文的相对熵进行分析计算比较后所获得的隶属度分析结果（非DKL的直接数值结果）。同理KLPD表示径向结果。

（2）定义故障判别向量K：

判别向量K中各分量被定义为：按照提出的隶属度函数式（7）和（8），对选定的频谱特征值进行判定、归一化后得到的占比概率值。实际中以第一种加工状态下的某一方向（轴向或径向）相关参数为基准，得到K1。以第二种加工状态下的同一方向相关参数为比较值，得到K2。通过K1 到K2 的变化获得K中各分量。“周期特性，频率分布发散特性，强化特性”各分量的获取：周期特性是对回转周期求余后获得的，频率分布发散特性、强化特性是从TOP20 点对频率的聚集分布特征中获得的。文中将结合实际问题，对各分量的获取方式及研究数据的数值分布特点进行详细的研究。

根据图4 定义的模糊子集，结合判别向量K（式（9）），设定理想故障分布向量P为：

图4 FUKL 融合算法结构Fig.4 The structure of FUKL fusion algorithm

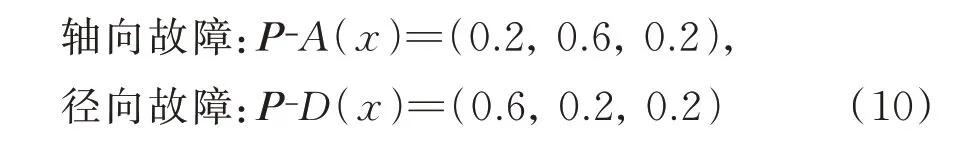
式（10）充分考虑“频率分布发散特性”（表现为轴向的发散特性）和“周期特性”（表现为径向规律性的摆动）分别作为A（x）（轴向故障）与D（x）（径向故障）的主要辨识特征占比较大，并根据与本文所研究故障机床同系列的多台机床连续3年相关售后维修历史数据中的故障特点及最终拆解维修结果的统计情况，对于此处基于式（9）建立的式（10），经综合分析后，将式（10）中P-A（x）内与式（9）“频率分布发散特性”分量对应的位置和式（10）中P-D（x）内与式（9）“周期特性”分量对应的位置的数值分别设定为0.6。“振幅强化特性”因其为辅助判定的共有特性，分析时设定占比较小，在式（10）的P-A（x）内，P-D（x）内，将与式（9）对应该分量的位置的数值设定为0.2。

（3）结果判定

依据故障判别向量K的形式，分别求取轴向、径向的实际特征判别向量Q与“轴向故障”、“径向故障”理想故障分布向量P的相对熵，相对熵小的即为故障倾向方向。进而可以量化出故障主轴系统在轴向或径向存在动刚度不足的相关故障倾向。

3 实验验证

3.1 验证对象及传感器布置

（1）验证对象

为验证所提算法的实用性、有效性、正确性，本文对存在加工颤振振纹故障的某台4075 系列型单主轴智能卧式车床进行相关验证研究。

如图5所示，经调整切削参数，更换刀具，排查装卡方式，修改加工走刀路径等，振纹没有变化。进行主要部件常规故障诊断也未发现明显损伤特征。根据第1 节对振纹成因的分析，考虑是由于加工过程中参与切削的机床相关主要部件存在动刚度不足相关故障所致。这些可能因素为：主轴系统动刚度不足、刀具进给系统动刚度不足、床身地脚动刚度不足，主电机异常振动。但无法确定究竟是哪一因素。

图5 故障机床所加工零件表面出现的振纹Fig.5 Chatter marks on the surface of parts machined by the faulty machine tool

（2）振动传感器布置

根据工程实际中行业内常用的、共识的检测切削验证效果的核心关注部位，结合对象机床的特点，设计选取如图6 和7所示的四个位置布置振动传感器，具体传感器的位置、用途与作用参阅表1。

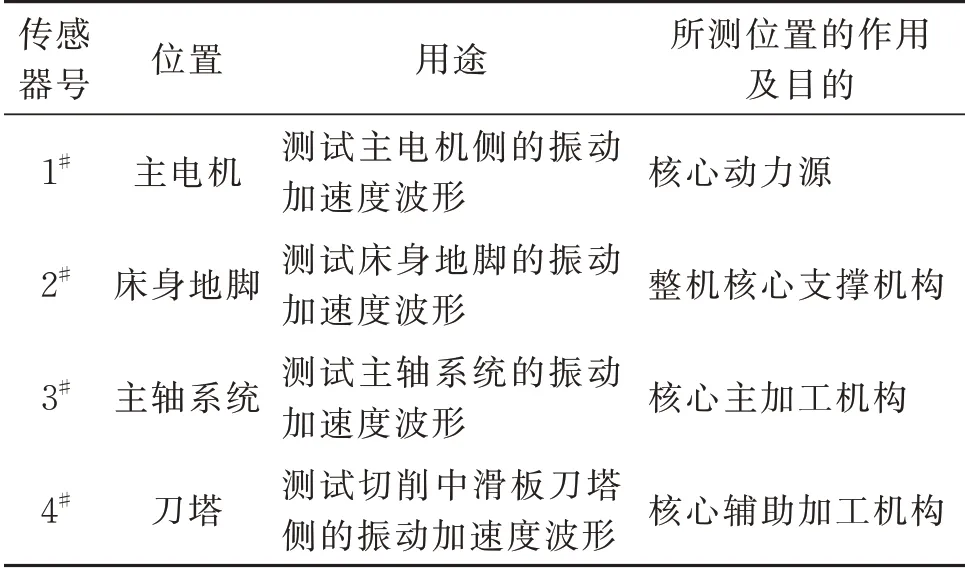
表1 传感器的布置与用途Tab.1 Arrangement and application of sensors

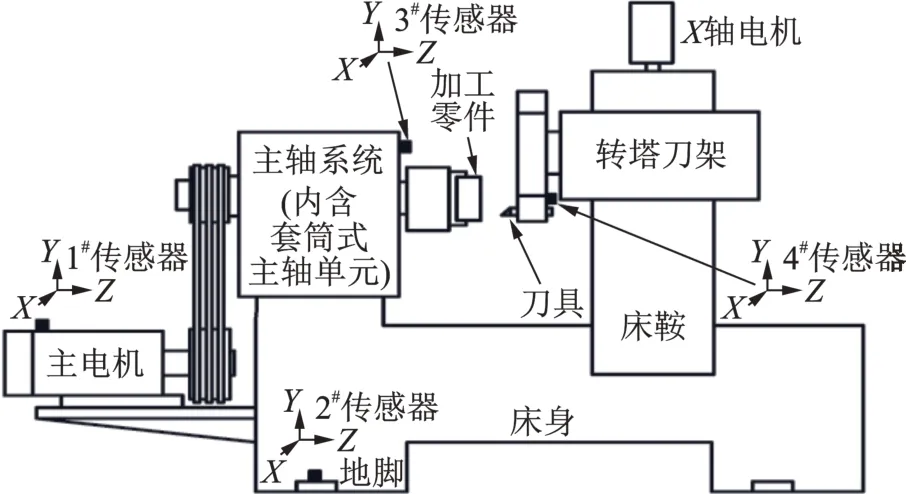
图6 振动传感器测试点布置方案Fig.6 Layout scheme of vibration sensor test points

图7 测试点的传感器安装位置图Fig.7 Sensor installation location map of test point

（3）实验切削参数

机床切削参数设置：主轴转速SP=500 r/min。实验用切削材料：45#钢，空心端面直径为150 mm，实心端面和外圆直径均为98 mm。

3.2 测试数据

测试数据包括：实心端面（0.5，0.75，1.0，1.25，1.5 mm 切深）、实心外圆（0.5，0.75，1.0，1.25，1.5 mm 切深）、空心端面（0.5，1.0 mm 切深）12 种加工参数下1#，2#，3#，4#传感器各3 个方向（X，Y，Z）的振动加速度波形数据。

3.3 基于PCA/D-S 的动刚度薄弱部件粗判别验证

3.3.1 实验过程

（1）数据的预处理及特征值提取

此处选择基于小波基sym8 的自适应软阈值重构滤波的方式，对于待研究的波形进行预处理，以滤除干扰噪声。在研究中为便于比较分析，选取实心材料的120 组数据进行比较，空心材料类同。

①时域波形特征值提取

对预处理后的波形，按照2.2.1 节的论述，选取各组数据的12 项时域波形特征。

②频域频谱特征值提取

采用FFT 变换方法，依次对120 组数据进行时频变换（如图8所示）（采样时长为14 s，采样频率65536 Hz）。结合PCA/D-S 算法的研究需要及2.2.2 节的分析，确定选取“频谱振幅中位数”、“频谱振幅平均值”、“功率谱平均值”作为频谱特征值。与本节（1）①中的12 项时域特征数一起共15 维时频特征数据，构成算法的输入特征数据，如表2所示。

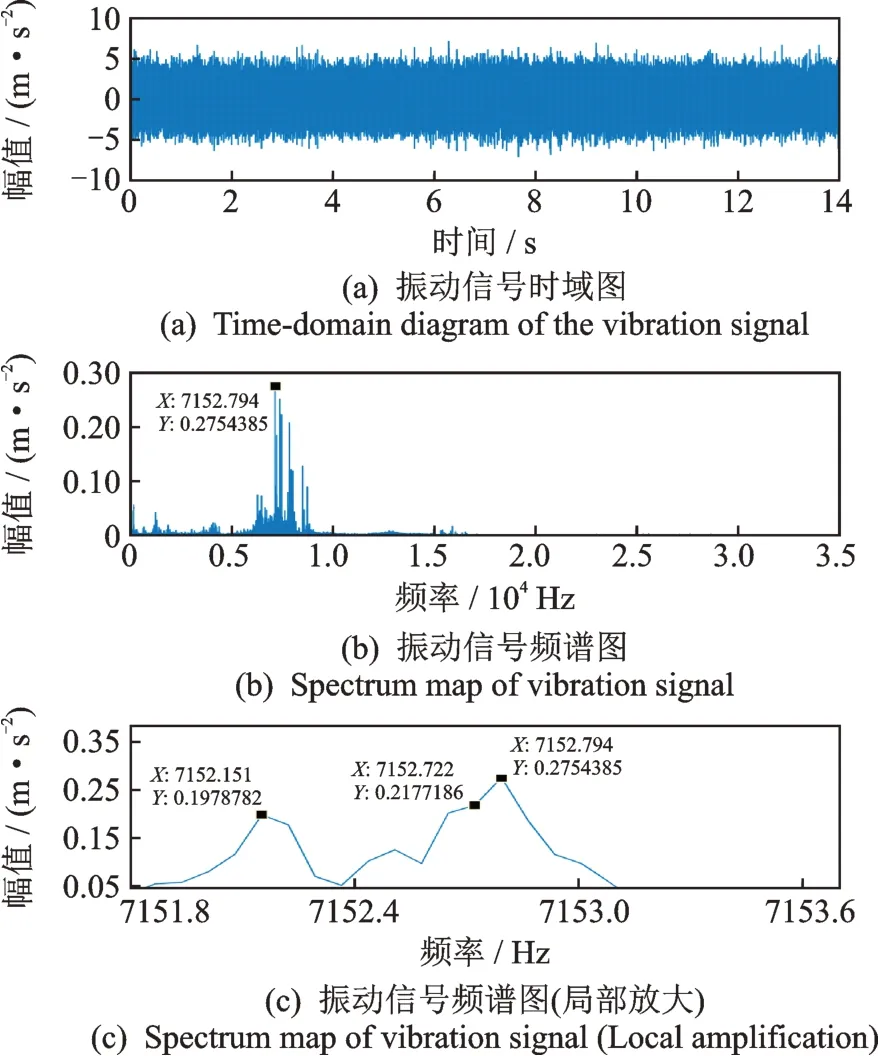
图8 3#传感器X 向在实心端面0.5 mm 切削时的频域频谱Fig.8 Frequency domain spectrum of 3# sensor when cutting 0.5 mm solid end face in X direction

（2）PCA 数据降维和数据变化均值可视化

使用PCA 降维的目的：将表2 的15 维时频高维数据降为三维，获得低维主成分特征，构成三维空间内的一个点，便于对特征变化的进一步研究。

表2 输入特征数据Tab.2 Input characteristic data

使用PCA 降维的原因：PCA 降维较同类方法能在较小的误差损失下，获得数据的主要特征，PCA 降维的最初三维特征含有原数据99%以上的可变性。

使用PCA 降维后的结论：很好地融合了15 维时频特征数据，获得了1#～4#传感器在5 种工况条件下的三维特征数据集。

这里对PCA 的数据降维效果及数据均值变化情况进行可视化对比分析（如图9～14所示）。设定：“EXD，EYD，EZD，EXW，EYW，EZW”分别为1#～4#传感器X向、Y向、Z向实心端面、实心外圆切削时的数据分析判定视角（“D”代表端面，“W”代表外圆）。

以图9 为例（其他类同），图上展示了1#～4#传感器各自5 种工况参数的PCA 降维数据在三维空间的分布结果。每类图标相邻点之间的连线（欧氏距离）表示临近工况之间的时频数据变化。根据2.2节的分析，这种变化包含时域、频域的有效特征数据的变化幅度，这些变化幅度从多个角度比较全面地表征了机床相应部件对于外部切削工况变化所产生的规律性、渐变性扰动的反映情况。图9 中红色三角形图标相邻点间连线长度均值明显大于其他三种颜色图标的。其他图类同。故可从图9～14 内的各传感器对应距离大小获得对应部件动力响应特性变化的直观表征。具体数值汇总如表3所示（表3 中特征变化均值为：对应5 种工况参数下相邻点之间的欧氏距离的均值）。

图9 实心端面X 向4 传感器5 工况降维数据可视化比较Fig.9 Visual comparison of dimension reduction data of solid end face X direction 4 sensors under 5 working conditions

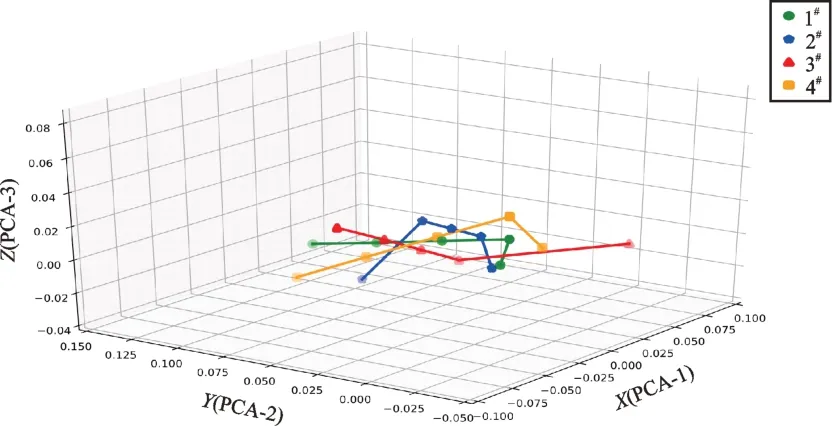
图10 实心端面Y 向4 传感器5 工况降维数据可视化比较Fig.10 Visual comparison of dimension reduction data of solid end face Y direction 4 sensors under 5 working conditions

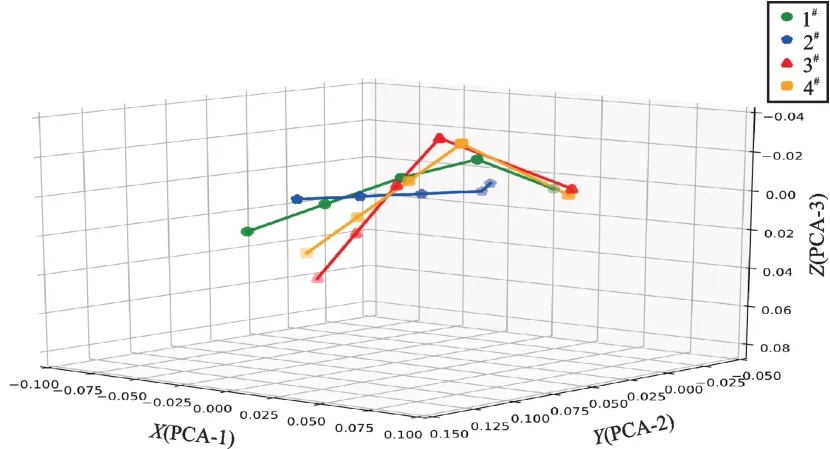
图11 实心端面Z 向4 传感器5 工况降维数据可视化比较Fig.11 Visual comparison of dimension reduction data of solid end face Z direction 4-sensors under 5 working conditions

图12 实心外圆X 向4 传感器5 工况降维数据可视化比较Fig.12 Visual comparison of dimension reduction data of solid excircle X direction 4 sensors under 5 working conditions

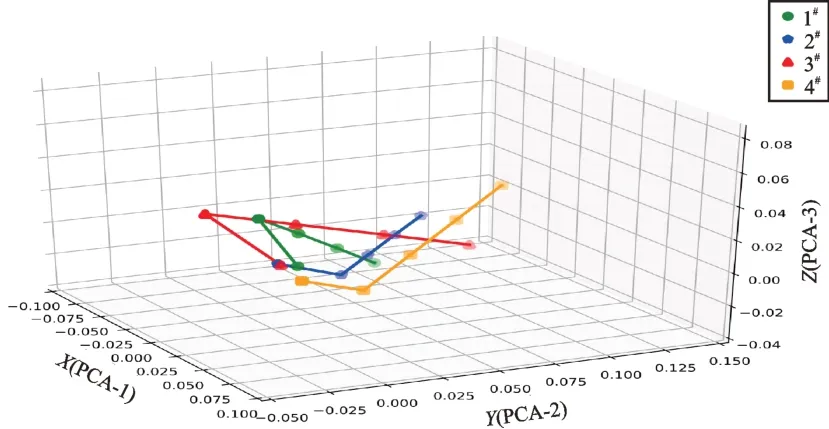
图13 实心外圆Y 向4 传感器5 工况降维数据可视化比较Fig.13 Visual comparison of dimension reduction data of solid excircle Y direction 4 sensors under 5 working conditions

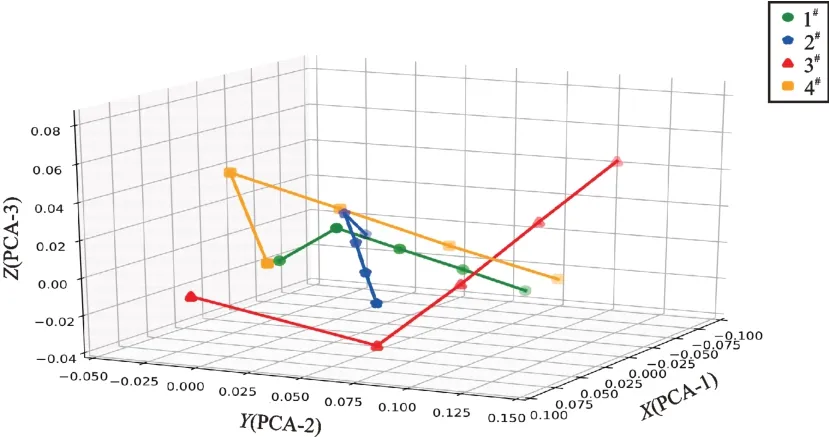
图14 实心外圆Z 向4 传感器5 工况降维数据可视化比较Fig.14 Visual comparison of dimension reduction data of solid excircle Z direction 4 sensors under 5 working conditions

（3）基于D-S 理论的多传感器信息特征辨识

①基于D-S 证据理论的模型建立

根据3.3.1 节（2），已建立“EXD，EYD，EZD，EXW，EYW，EZW”6 个判定视角。

②特征数据的选取

选表3 中“特征变化均值”作为判别特征数据。

③建立信任配比函数

对表3 中“特征变化均值”列内的数据，进行特征变化均值的对应判定视角组内占比计算，范围设定为［0，0.95］，取不确定度为N**({ω})=0.05（此处不确定度0.05 数值的确定，是考虑在3.1 节（1）中分析主要故障部件时可能存在的误差影响），计算数据，得到对应证据信息见表3 倒数第二列。

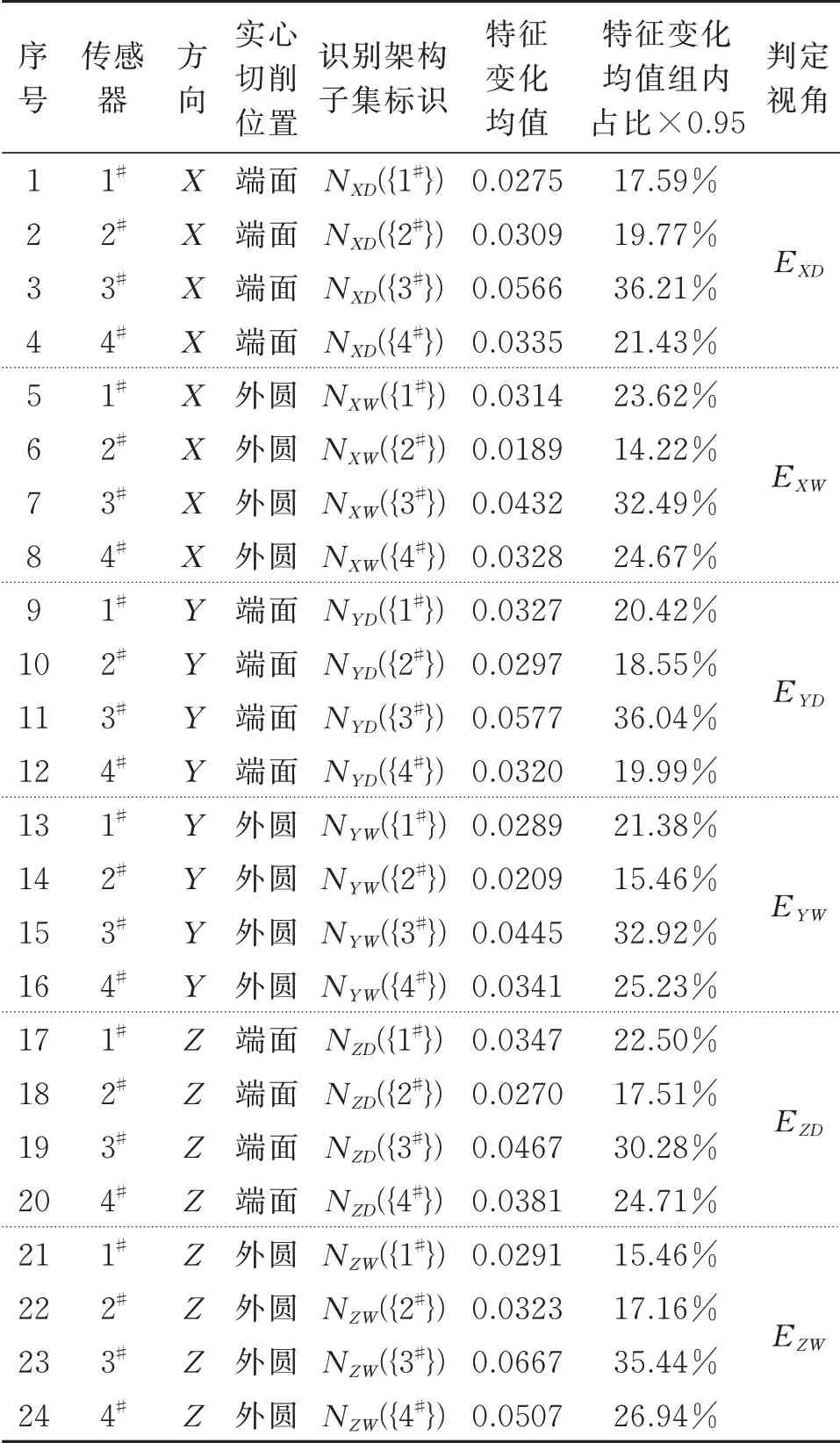
表3 特征变化均值汇总Tab.3 Summary of mean value of characteristic change

3.3.2 实验结果

（1）计算新融合的N（｛1#｝）合成证据概率，等价于求6 项证据合成的交集｛1#｝的可信度的和，即：

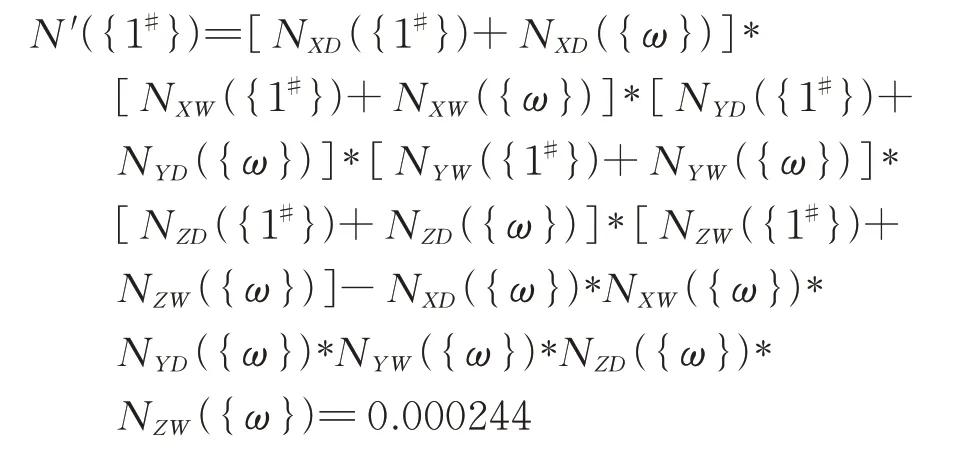
同理：N′（｛2#｝）=0.000114；N′（｛3#｝）=0.0034；N′（｛4#｝）=0.000562；N′（｛ω｝）=0.000001

（2）进行归一化处理

根据D-S 合成规则，结合式（4），可得：

1-T=N′（｛1#｝）+N′（｛2#｝）+N′（｛3#｝）+N′（｛4#｝）+N′（｛ω｝）=0.004321；所以D-S 运算结果为：

N({1#})=0.000244/0.004321=0.0565；

N({2#})=0.0264；N({3#})=0.7869；

N({4#})=0.1301

3.3.3 实验小结

上述N（｛1#｝）～N（｛4#｝）结果中，N（｛3#｝）的合成证据概率78.69%明显高于其他3 个传感器对应的数据，故对于该故障机床，主轴系统是动态切削条件下的薄弱环节，动刚度相对薄弱，需做溯源研究，以最终确定故障本质。

合成证据概率是依据提出的PCA/D-S 算法，对4 个传感器在5 种工况下的振动变化特征值（见表3的“特征变化均值”）进行数据合成的结果，是以数值形式表示不同判定视角内同一传感器的全部特征变化占4 个传感器总体变化的百分比。数值界定的根据是在4 个传感器中，单一传感器的合成证据概率是4 个传感器各自概率均值25%的2 倍以上，即占据总体1 的多数概率比例，即可进行最大倾向判定。

由于本文的研究主旨是在存在加工颤振故障的机床范围内，验证所提出的能够量化溯源该机床动刚度薄弱部件的方法，所比较的是故障机床各部件间的差异，以便进一步溯源故障源部件，并且不同机床的同部件因不同机床装备整体的配合不同，在切削过程中所表现出的动刚度会存在差异，故不进行不同机床之间的比较，仅研究选定的故障机床。

3.4 基于FUKL 的细粒度故障溯源验证

3.4.1 实验过程

通过3.3 节的研究，已从该台故障机床的多个部件中辨识出主轴系统动态刚度薄弱，为进一步溯源故障，这里基于2.4.2 节提出的FUKL 融合算法，对主轴系统内部的故障特征做进一步辨识研究。

对图6 中主轴系统侧3#传感器所测的数据进行频域频谱幅值特征提取。特征提取的目标是根据式（9）向量K获得实际特征判别向量Q的3 个特征分量：周期特性，频率分布发散特性，振幅强化特性。

（1）发散特性与强化特性研究

选取对应频谱的幅度值最大的20 个点（TOP20）作为研究判定对象。图8（c）展示了3#传感器X向对应切削条件的部分TOP20 点。图8（c）是对图8（b）X向放大18000 余倍获得的幅值最大点附近的单个数据点间隔的局部放大图示。图8（b）的TOP20 点的获取是基于图8（b）对应频谱的所有点逐点比较后获取的，图8（b）为分辨率（X轴）较低的频谱粗线条轮廓图示。

图15 和16 是关于对应切削方向（X向，Z向）的TOP20点的频率、幅值的散点图。以图15为例，7400 Hz处对应切深0.5 mm 的散点数量为4个，对应切深1 mm 的散点数量也为4 个，这8 个点纵向基本在1 列上，即在TOP20 点中基于对应切深0.5 mm 的4 个散点，该对应切深1 mm 的4个散点表现为强化特性。而8600～8800 Hz 内的1 个切深1 mm 散点，由于没有切深为0.5 mm 的同频率同样数量的散点与其对应，故切深1 mm 的TOP20 中该点表现为发散特性。依此方法，图15 上强化特性的点的数量总计为16 个，发散特性的点的数量为4 个。同理，图16 上强化特性的点的数量为12个，发散特性的点的数量为8个。

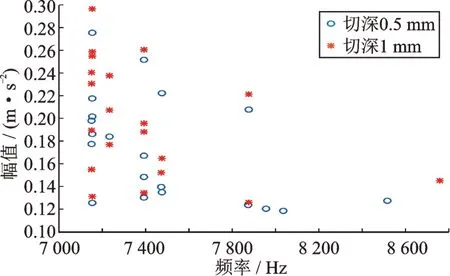
图15 3#传感器的X 向在实心端面0.5 mm，1 mm 切削时测得的频域频谱的TOP20 数据分布差异对比Fig.15 Comparison of TOP20 data distribution difference of frequency domain spectrum measured by X-direction of 3# sensor when cutting 0.5 mm and 1 mm solid end face

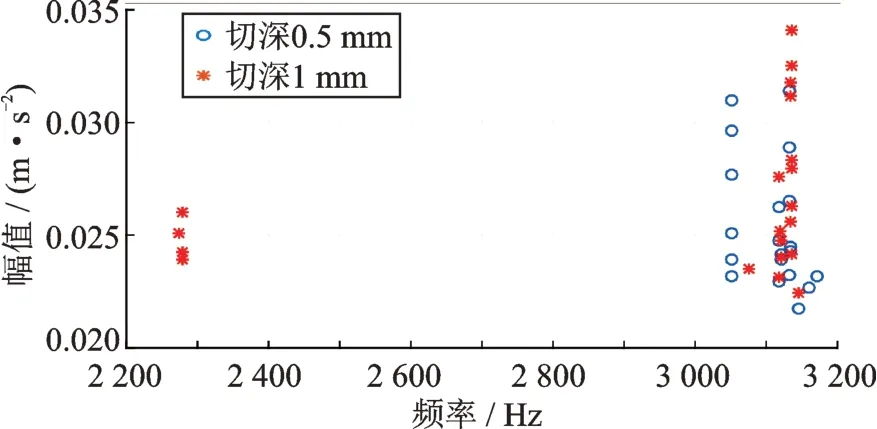
图16 3#传感器的Z 向在实心外圆0.5 mm，1 mm 切削时测得的频域频谱TOP20 数据分布差异对比Fig.16 Comparison of TOP20 data distribution difference of frequency domain spectrum measured by Z-direction of 3# sensor when cutting 0.5 mm and 1 mm solid excircle

（2）周期特性研究

关于周期特性，本文提出的确定方法：将切深0.5 mm（此处选择0.5 mm 的目的是尽量减少切削力对于主轴系统故障诊断的冲击影响）的TOP20 的频谱点的对应频率值对该切削状态的回转频率进行求余数比较。采用的机理是：如果存在主轴系统径向不对中故障，会在外部施加切削力的情况下放大这种固有故障，幅值TOP20 的频率点的频率值如果与该回转频率呈现整数倍关系，即求余余数越小，这种关系越近，即可反映回转径向不平衡故障的影响。本文切削条件中SP=500 r/min，对应回转状态变化周期频率为8.33 Hz。上述TOP20 的频谱点对应的频率对周期求余后，余数小于1 Hz 的个数，即余数小于周期频率8.33 Hz 的12%（1/8.33）的点的个数，认为和周期性密切相关。此研究的目的是满足特征横向对比研究的需要。相关结果如图17 和18所示。

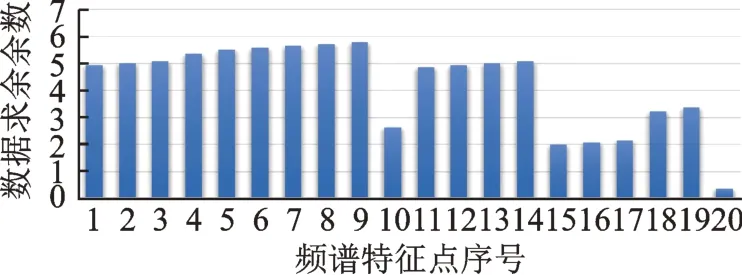
图17 3#传感器X 向在实心端面0.5 mm 切削时的频率求余分布Fig.17 3# sensor frequency complementary distribution of X direction when cutting 0.5 mm solid end face

图18 3# 传感器Z 向在实心外圆0.5 mm 切削时的频率求余分布Fig.18 3# sensor frequency complementary distribution of Z direction when cutting solid excircle 0.5 mm

3.4.2 实验结果

对图15～18 的数据进行汇总，如表4所示。表4中“TOP 20 的周期性占比”表示符合周期特性的点数/20。“TOP 20 的发散性占比”表示符合发散特性的点数/20。“TOP 20 的强化性占比”表示强化特性的点数/20。

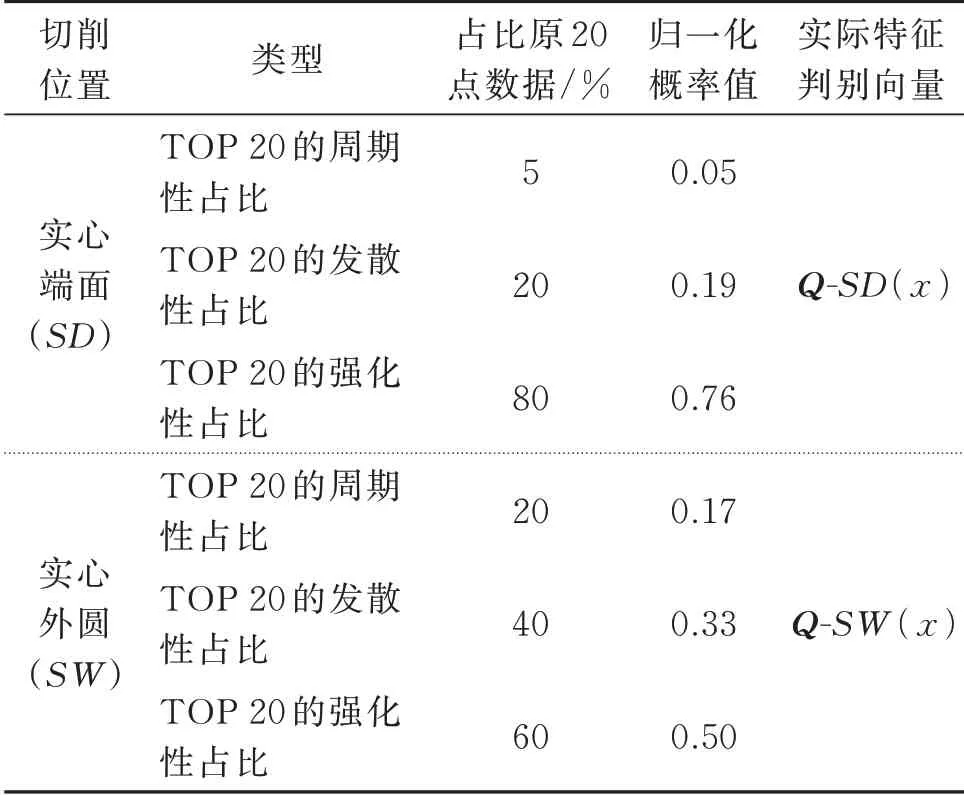
表4 数据占比统计Tab.4 Statistics of data proportion

采用2.3.4 节中的相对熵计算公式（6），分别计算实际特征判别向量Q-SD(x)，Q-SW(x)与理想故障分布向量P-A(x)，P-D(x)（式（10））的相对熵：

DKL(P-A(x)‖Q-SD(x))=0.7002

DKL(P-A(x)‖Q-SW(x))=0.2079

DKL(P-D(x)‖Q-SD(x))=1.2342

DKL(P-D(x)‖Q-SW(x))=0.4733

3.4.3 实验小结

经过计算，发现上述4 种实验结果中无论是在进行实心端面还是实心外圆的切削中，针对振动频谱信号TOP20 的幅度值，采用基于故障判别向量K的形式获得的实际特征判别向量Q，与各自理想故障分布向量P的相对熵的计算结果比较中，都是轴向比径向的相对熵要小。所以，通过提出的FUKL融合算法的研究结果，可以确定该故障机床的主轴系统在轴向存在引起动刚度不足相关故障的特征。从而量化判定出该机床加工颤振问题产生的根源。

3.5 算法优势分析

（1）多维数据研究与单一数据研究的优势对比

在很多研究中，对于机床多组件的检测数据提取往往基于单一特征，如峭度等，这会人为带来对研究问题特征选取时的片面性。本文提取的时频域多维有效特征能全面、客观地反映不同状态特征的变化，并通过结果验证了方法的有效性与正确性。

（2）PCA/D-S 算法的优势

对于机床的故障诊断，往往面临“贫数据集”问题。在对于受加工状态切削高频振动影响较大的动刚度问题的研究中，要辨识出多位置动刚度的薄弱环节，得出有力的量化结果，使用本文提出的PCA/D-S 算法效果突出，数理特征明显。表5 中方法1～4 对应的“方法的准确性”是基于本文的120 组数据，以最终拆解后得到的客观故障根源为正确结果，使用每种方法各进行20 次研究，统计正确研究结果次数的占比。“方法的耗时”为单次研究耗时。

表5 算法效果比较Tab.5 Comparison of algorithm effect

（3）FUKL 融合算法的优势

本文提出的FUKL 算法不仅针对研究问题融合了算法本身的特征，同时在故障判别向量K的构建上，充分融合了主轴系统径向、轴向的故障特征。与多种方法、算法相比，其优势明显（如表6所示）。

表6 算法特点比较Tab.6 Comparison of algorithm characteristics

3.6 拆解故障部件溯源结果

因本文所研究的主轴系统为由单根套筒式主轴单元直接构成，无齿轮传动，且在实验验证前已排除卡具等其他因素（见3.1 节（1）及图6），根据第1 节的分析，为进一步追溯故障根源及验证所提方法，对上述问题机床的主轴系统进行拆卸，将主轴系统内的套筒式主轴单元拆下，放在机床主轴综合加载检测试验台上进行检测，如图19 和20所示。

如表7所示，该故障机床适配的主轴单元的轴向、径向刚度合格标准分别为350 N/μm 和560 N/μm。从表7 可知，该机床的轴向静刚度低于合格标准，出现故障。即最终溯源出产生故障的根源为静刚度不足。在更换合格的主轴单元后，该机床的切削颤振故障消失。该结果一方面说明了由于该套筒式主轴单元自身存在静刚度不足的弱故障，进而产生了由该主轴单元构成的主轴系统在切削中所表现出来的动刚度不足问题。另一方面，也从实际检测的角度验证了使用本文所提算法通过判别动刚度不足，进而溯源辨识机床主轴系统动刚度不足相关弱故障问题的有效性及轴向方向判别的正确性。