交互偏移支持矩阵机及其在滚动轴承故障诊断中的应用

徐海锋，潘海洋，郑近德，童靳于

（安徽工业大学机械工程学院，安徽马鞍山 243002）

引言

滚动轴承作为机械设备中的一类重要零部件，其工作时往往处于高速旋转的运行状态，长时间工作会致使滚动轴承等部件出现一定的疲劳损伤。因此，如何对滚动轴承的健康状况进行智能监测和诊断，已成为众多学者研究的热点内容与方向。

随着人工智能的发展，基于模式识别的滚动轴承智能故障诊断方法得到了广泛的研究和应用，如人 工 神 经 网 络（Artificial Neural Networks，ANN）［1］、K-最近邻（K-nearest Neighbor，KNN）［2］和支持向量机（Support Vector Machine，SVM）［3］等。上述方法通过不断完善，已被应用于故障诊断、文本分类、图像识别等领域。SVM 作为其中最稳定的一种分类方法，拥有良好的泛化能力和稀疏性。在解决二分类问题时，传统的SVM 通过将原始数据映射到一定维度特征空间，构造两个平行超平面来分割不同类型样本。当原始数据线性不可分时，如异或（Exclusive OR，XOR）问题，SVM 很难找到一对线性超平面对数据样本进行有效分割。针对该类问题，Li 等［4］提出多目标近似支持向量机（Multi-task Proximal Support Vector Machine，MPSVM），其通过求解两个广义特征值问题，构造出两个非平行的分类面对不同数据进行分割，能够较好应对异或问题；Chen 等［5］以经验风险最小化作为基本框架提出了孪生支持向量机（Twin Support Vector Machine，TWSVM），其将SVM 的优化问题转变为求解两个较小的线性规划问题，构造一对非平行的分类面，实现了分类效率的提升。为提高TWSVM 算法的泛化能力，Wang 等［6］在构造目标函数的过程中引入正则项，提出孪生有界支持向量机（Twin Bounded Support Vector Machine，TBSVM），其使用连续过度松弛技术（Successive Over-Relaxation，SOR）［7］和正则项解决模型凸优化和鲁棒性问题。

上述方法本质上都是基于向量进行建模和分类，当处理微弱故障信号的诊断问题时，仅提取若干故障可能无法完成故障的有效识别。为了解决该问题，Luo 等［8］受核范数的启发提出支持矩阵机（Support Matrix Machine，SMM），以矩阵样本作为直接输入，充分挖掘了矩阵行列间的结构信息，这为后续研究提供了新的思路，如鲁棒支持矩阵机（Robust Support Matrix Machine，RSMM）［9］、稀疏支持矩阵机（Sparse Support Matrix Machine，SSMM）［10］、多分类支持矩阵机（Multiclass Support Matrix Machine，MSMM）［11］等。但这类矩阵分类器通常是线性的，无法解决矩阵数据线性不可分的问题，同时，还存在训练误差大、过拟合等不足。鉴于此，Gao等［12］基于矩阵数据构造非平行分类器的思想，利用左右奇异值向量构造目标函数提出了一种孪生多秩支持矩阵机（Twin Multiple Rank Support Matrix Machine，TMRSMM）；Jiang 等［13］利用多秩左右投影矩阵替换左右投影向量来构造目标函数，提出了多秩多线性孪生支持矩阵机（Multiple Rank Multi-Linear Twin Support Matrix Machine，MRMLTSMM）。TMRSMM 和MRMLTSMM 利用左右投影思想解决了非线性矩阵数据的分类问题，且作为非平行超平面分类器（Nonparallel Hyperplane Classifier，NHC）的一类方法，它们在构造分类超平面时，遵循“寻找一对非平行的超平面，使得每一类样本聚集在相应超平面的附近，同时，另一类样本尽可能地远离该平面”的思想，提高了模型的分类精度。但是，当数据样本存在XOR 问题时，仅依靠非平行超平面和难以完成复杂数据的有效分割。

基于上述研究，考虑矩阵拥有保持数据结构信息完整的优势以及提高模型泛化能力的问题，本文提出一种新的矩阵数据分类方法——交互偏移支持矩阵机（Interactive Deviation Support Matrix Machine，IDSMM）。IDSMM 以矩阵作为输入与建模元素，通过构造一对交互超平面将两类复杂样本分割开来，使得正类样本靠近超平面b1=1，负类样本尽可能远离此平面。同时，引入多秩左右投影矩阵构造目标函数，使IDSMM 具有更好 的 数 据 拟 合 能 力 。 与 TMRSMM 和MRMLTSMM 方法相比，IDSMM 构造两个交互偏移超平面和，从几何学上看，两平面间的“间隔”将变大，每一个超平面距离异类样本更远，提高了模型的泛化能力。最后，为了验证所提方法的性能，采用两种不同的滚动轴承故障数据集进行验证，实验结果表明，与其他分类器相比，IDSMM 在滚动轴承故障诊断中具有更优异的分类性能。

1 交互偏移支持矩阵机原理

1.1 支持矩阵机

支持矩阵机是一种基于经验风险最小化的矩阵分类器，其利用铰链损失和正则项组合解决一个凸优化问题。同时，SMM 的核心思想是寻找两个平行超平面，将正负两类样本分割开来。为了得到两个超平面，构造目标函数如下式所示：

式中W∈Rm×m为权重矩阵，{Xi∣i=1，…，n}∈Rm×n为矩阵样本，yi=(-1，1)为对应类别标签，b为偏移量，为正则项，τ为正则项系数，为铰链损失函数，C为损失参数。

利用交替方向乘子法ADMM 可以解决目标函数（1）的求解问题，得到权重矩阵W和偏移量b。然后构建如下决策函数，对于新的未知样本，有：

SMM 是一种可以充分利用输入矩阵样本结构特征的分类器，其核心思想还是寻找两个平行的分类面，面对一些复杂数据时，很难有效地找到两个平行分类超平面去划分两类样本。

1.2 交互偏移支持矩阵机

SMM 方法的核心在于寻找一个最优分类面Tr(WTX)+b=0 对不同数据进行划分，根据VC间隔理论，在距离超平面处，分别存在上下边界Tr(WTX)+b=1 和Tr(WTX)+b=-1，两个边界间的距离称为最大间隔。由于这种平行超平面的构造形式，使得SMM 无法有效处理一些复杂数据。为了解决这个问题，IDSMM 采用一对交互偏移超平面，同时，不同于以往NHC 方法的超平面构造形式，IDSMM 拟将交互偏移超平面构造为和为了实现这个目标，尽可能使目标函数中的和最小。这两项在目标函数中表示每一类样本与相应超平面的平方距离的和。通过最小化这两项，使得正类样本尽可能地接近并远离，同时，负类样本尽可能的接近并远离b1=1。IDSMM 方法的详细步骤如下：

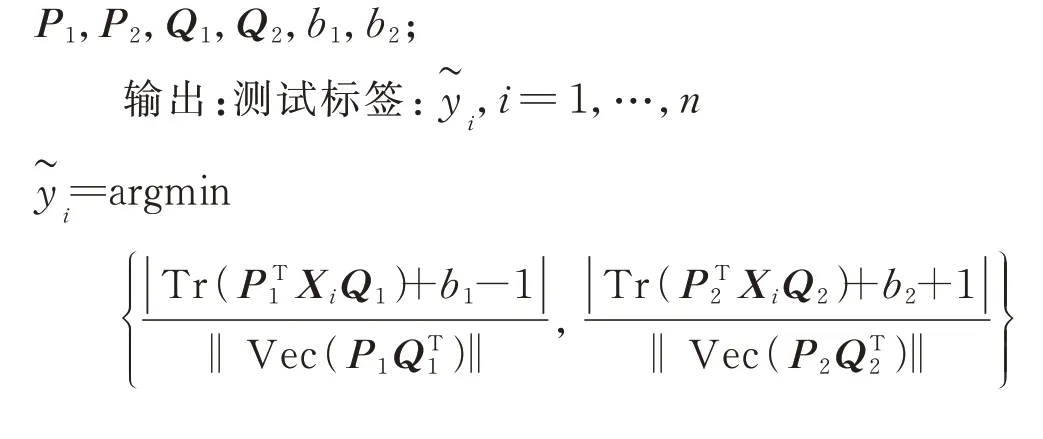
2 实验分析

为了验证本文提出的IDSMM 的分类性能，本节分别使用安徽工业大学滚动轴承故障振动信号数据集和湖南大学锥齿轮-滚动轴承故障振动信号数据集对其进行测试和分析，采用Accuracy，Recall，Precision，F1-score 和Kappa 作为模型评价指标。Accuracy 为正确率，是最常用的分类性能衡量指标，表示所有测试样本中分类器能正确分类的占比；Recall 表示召回率，指在实际的测试样本中，被分类器正确识别出来的正类样本占比；Precision 表示精确率，指测试的正类样本中，真正能被模型识别出来的属于正类的样本占比；F1-score 为精确率和召回率的调和值；Kappa 系数常用于一致性检验，用于判断模型的分类精度。以上五种指标在一定范围内，值越大，表示模型的分类性能越好。

同时，为了验证所提方法的优越性，选择SMM，SSMM，RSMM 和MRMLTSMM 作为对比（所有实验均在Intel（R）Core（TM）i5（2.20 GHz），RAM 8 GB 计算机上的Matlab2019b 运行）。由于SMM，RSMM，SSMM，MRMLTSMM 和IDSMM 等方法的输入元素为矩阵，需要构造输入矩阵来完成分类和建模。辛几何相似变换方法［15］作为一种新的信号降噪与分析方法，已被证明具有良好的特征提取能力，因此，本文拟采用辛几何相似变换分析原始信号，以获得可以保存完整结构信息的辛几何系数矩阵。

IDSMM 的分类流程结构如图1所示：1）将不同状态的数据作为训练集，通过辛几何相空间重构后输入到主程序，得到决策函数（30）；2）将不同状态的数据作为测试集输入到决策函数（30）；3）对不同的模型采取同样的方法完成测试，并进行对比分析。

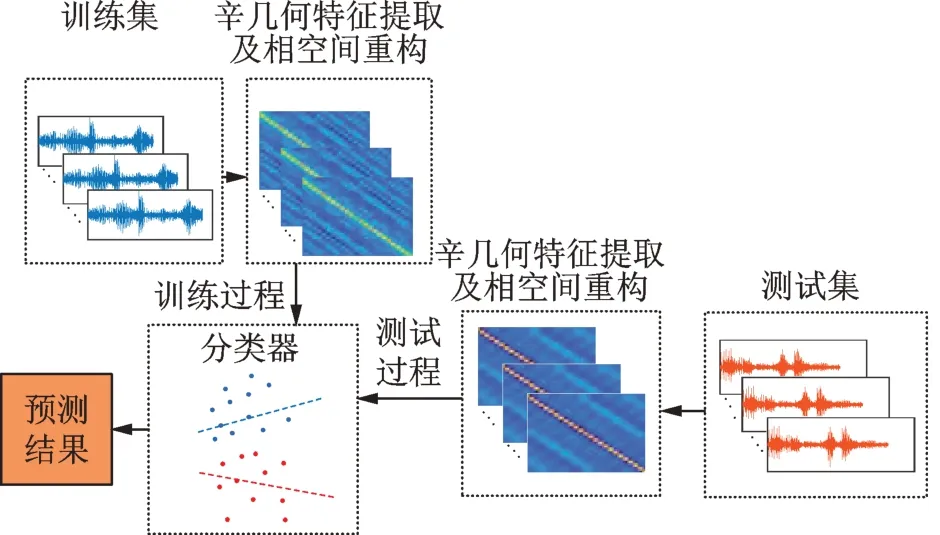
图1 分类流程图Fig.1 Classification flow chart

2.1 实验1

为了验证本文所提方法的分类性能，选择安徽工业大学滚动轴承故障振动信号数据集进行分类测试。滚动轴承故障模拟试验台如图2所示。试验所用轴承型号为SKF 6205 深沟球轴承，使用电火花加工技术分别在轴承上布置出内圈故障、外圈故障和滚动体故障。试验过程中，设置负载为5 kN，主轴转速为900 r/min，采样频率为10240 Hz。同时，利用加速度传感器分别采集滚动轴承在正常状态、内圈故障状态、外圈故障状态及滚动体故障状态下的加速度信号，详细试验滚动轴承状态和试验参数见表1（实验选择260 组训练和测试样本）。

图2 滚动轴承故障模拟试验台Fig.2 Roller bearing fault simulation test bench

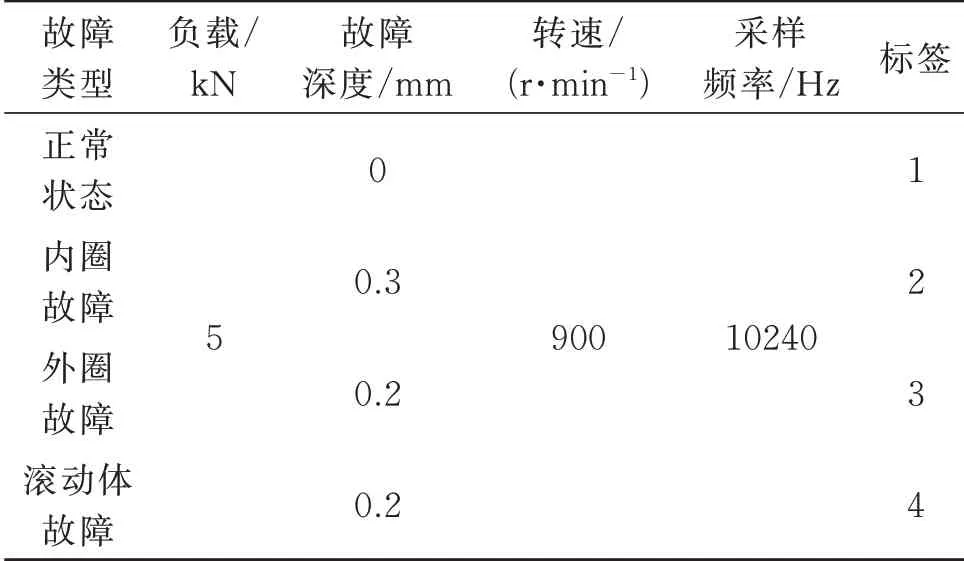
表1 滚动轴承试验参数Tab.1 Experimental parameters of rolling bearings

IDSMM 的性能与参数K，C1，C2，C3和C4相关，因此需要在训练前选择最优值。首先，根据文献［6，13］相关取值方法，通过实验取C1=0.1，C2=0.1，C3=0.01 和C4=0.01。此外，对于参数K，设置K的取值范围为1～10，选取180 组训练和测试样本并采用5 折交叉验证进行实验。图3 为IDSMM 在K为1～10 范围内得到的五种指标对比，表2 为训练时间。

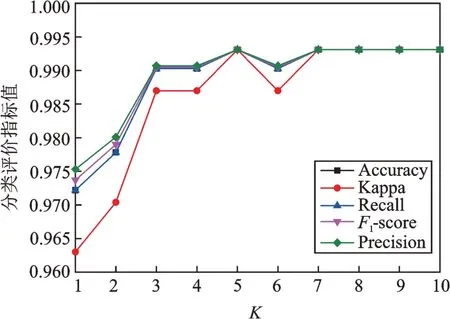
图3 不同K 的IDSMM 五种指标对比Fig.3 Comparison of five indicators of IDSMM in different K

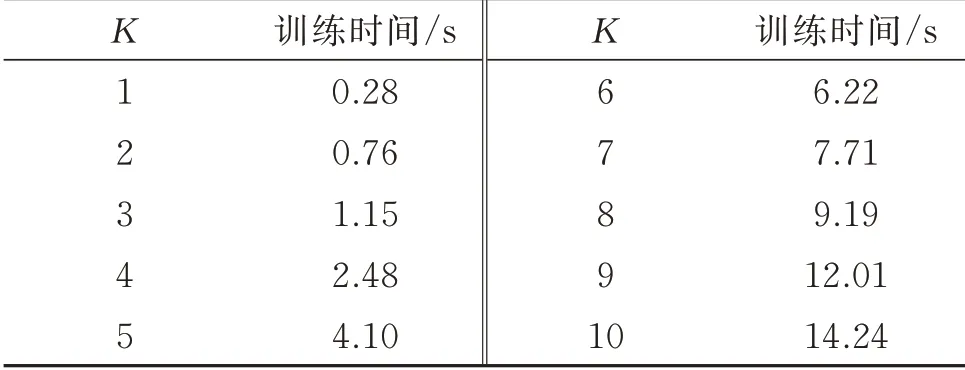
表2 不同K 的IDSMM 训练时间Tab.2 IDSMM training time in different K

从图3 中可以看出，IDSMM 分类器在不同的K下均能够保持较高的准确率。总体上，随着K的增大，各个指标逐渐增大，最终保持平稳状态，且K=5或K≥6 时分类准确率最高。IDSMM 采用交替迭代求解左右投影矩阵，随着K值的增大，P1，P2，Q1和Q2的矩阵尺寸增大，模型计算的复杂度增大，从而使得耗时越来越长。因此，为了使IDSMM 分类性能达到最佳的同时缩短训练时间，选择K=5 作为模型的输入参数，此时五种指标均处于较高水平，训练用时相对较短。

IDSMM 采用SOR 方法求解对偶问题，通过交替迭代求解最优P1，P2，Q1和Q2。图4 展示了该模型在训练过程中交替求解P1，P2，Q1和Q2的收敛过程曲线。由于P1，Q1和P2，Q2分别求解，所以会有两条不同的收敛曲线，其中，P1和Q1表示求解P1和Q1过程中目标函数（5）的收敛曲线，P2和Q2表示求解P2和Q2过程中目标函数（6）的收敛曲线。从图4 可以看出，IDSMM 经过较少的迭代次数可以快速达到收敛状态。

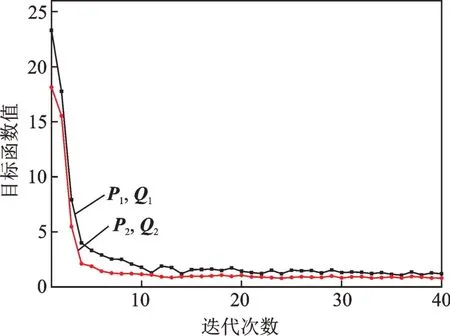
图4 IDSMM 收敛曲线Fig.4 IDSMM convergence curve

SMM，RSMM，SSMM 和MRMLTSMM 模型中均具有不同的参数，为了保障测试的客观性，采用5 折交叉选择各个参数，五种分类器的最终参数选择如表3所示。然后，分别使用IDSMM，SMM，RSMM，SSMM 和MRMLTSMM 对100 个样本进行训练，得到五种预测模型，再用160 个样本进行测试，识别结果如图5所示，从图中可以看出，IDSMM将第1 类和第4 类的样本错分，其他类别全部被正确分类。SMM，RSMM 和SSMM 存在较多第4 类错分给第3 类的样本，MRMLTSMM 方法错分率较低。表4 为五种分类器的五种指标对比，从表中可以看出，IDSMM 五个指标均最高，表示IDSMM 模型有着最好的分类性能。

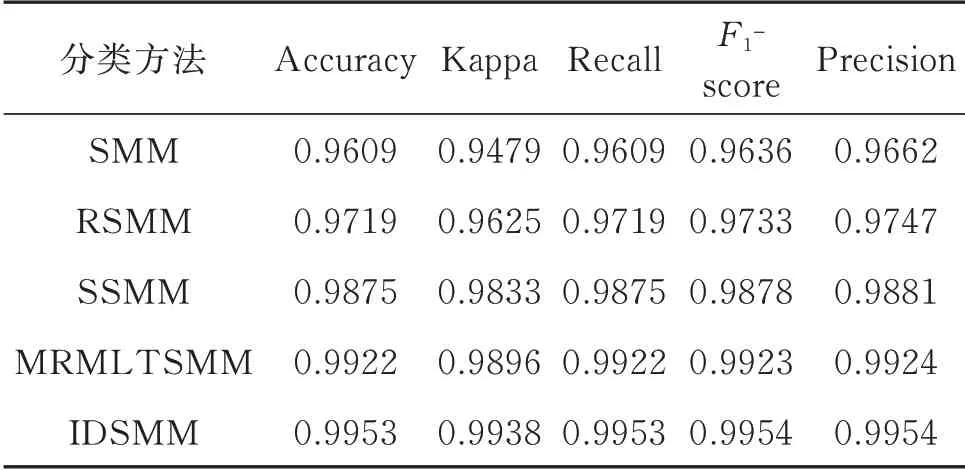
表4 五种方法的分类性能对比Tab.4 Comparison of classification performance of five methods

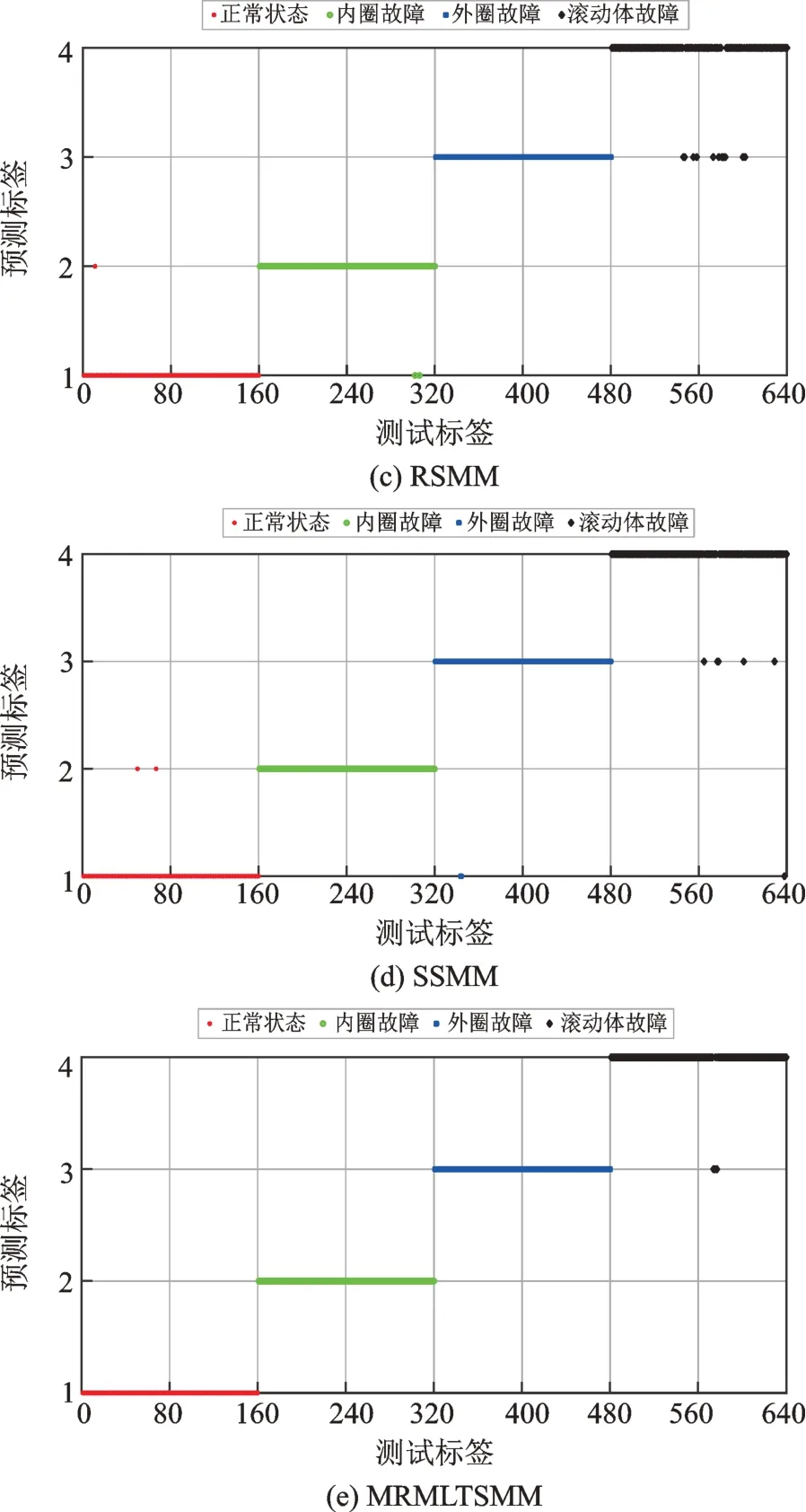
图5 五种方法分类结果Fig.5 Classification results of five methods

表3 五种方法的参数Tab.3 Parameters of five methods

为避免偶然因素的发生，得到更好的测试结果，选择260 个样本采用5 折交叉验证方法再次进行测试。图6 展示了五种分类器分别在5 折交叉验证下得到的结果（1～5表示每次的分类准确率）。从图6中可以看出，IDSMM 分类性能最好，平均分类正确率达到99.62%，SMM，RSMM，SSMM 和MRMLTSMM的平均分类正确率分别为96.25%，97.89%，98.56%和99.04%。IDSMM 方法在构造分类面时，其为不同的样本分别构造对应的分类面，得到一对交互偏移分类超平面，能够更有效地处理复杂数据，同时，IDSMM 采用左右投影矩阵方法，降低了过拟合的影响。其次，相比MRMLTSMM，IDSMM 的分类面间的间隔增大，从而使分类性能提高。SSMM 方法同样采用构造一对交互超平面进行分类，同时其模型本身具有稀疏属性，也实现了较为出色的分类性能。尽管RSMM 在建构模型时提高了鲁棒性，但在此复杂数据下未表现出良好的分类性能。SMM是一种基于经验风险最小化的分类器，其使用常规的方法来构造两个平行的分类超平面，模型的泛化能力较差，因此分类结果不佳。

图6 5 折交叉验证下五种方法的结果Fig.6 Results of five methods in 5-CV

综上所述，IDSMM 分类方法具有良好的分类性能，其模型参数在一定范围内，对整体模型的影响有限。同时，实验验证了其收敛的有效性，在较短的时间内，该方法能够得到最优解并完成训练和测试。

2.2 实验2

IDSMM 在安徽工业大学滚动轴承故障振动信号数据集上展示了良好的分类性能，为了进一步验证论文提出方法的性能，选择湖南大学锥齿轮-滚动轴承故障振动信号数据集再次进行分类测试。试验采用的轴承为型号SKF 6206。试验过程中，设置载荷为4 kN，电机转速为900 r/min，采样频率为8192 Hz。轴承故障信息和试验参数如表5所示（选择350 组训练和测试样本）。

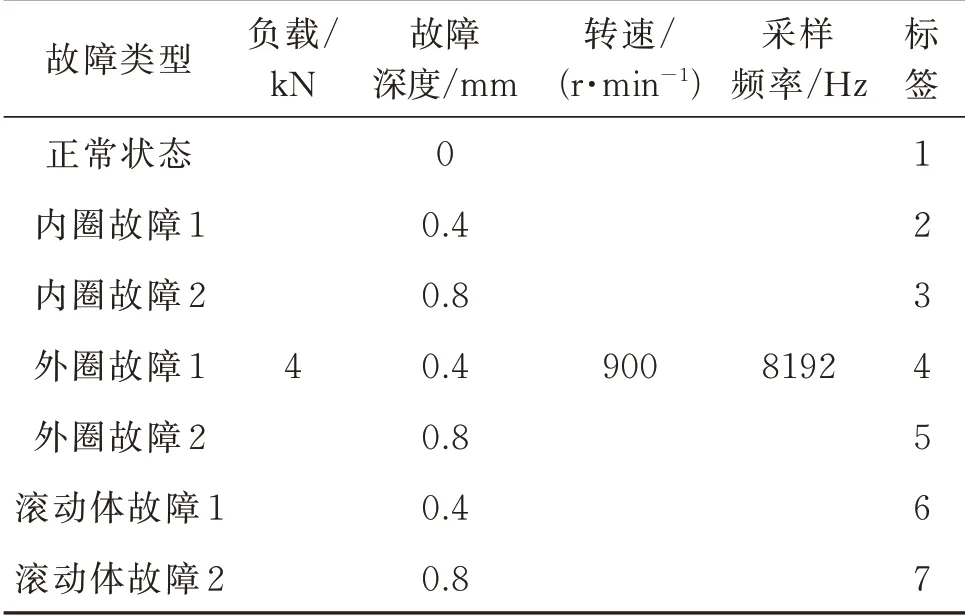
表5 滚动轴承试验参数Tab.5 Experimental parameters of rolling bearings

图7 展示了IDSMM 方法在K为1～10 范围内选择180 组训练和测试样本进行实验得到的五种指标对比，表6 为训练时间。从图7 中可以看出，当K=4，模型分类正确率达到100%。随着K增大，IDSMM 分类性能明显提升，K≥3 以后，分类准确率、召回率、F1-score 和Kappa 均处于较高水平。说明该模型在K≥4 的情况下能达到最佳的分类性能，但K值越大，训练用时越久。基于以上分析，选择K=4 作为模型的输入参数。

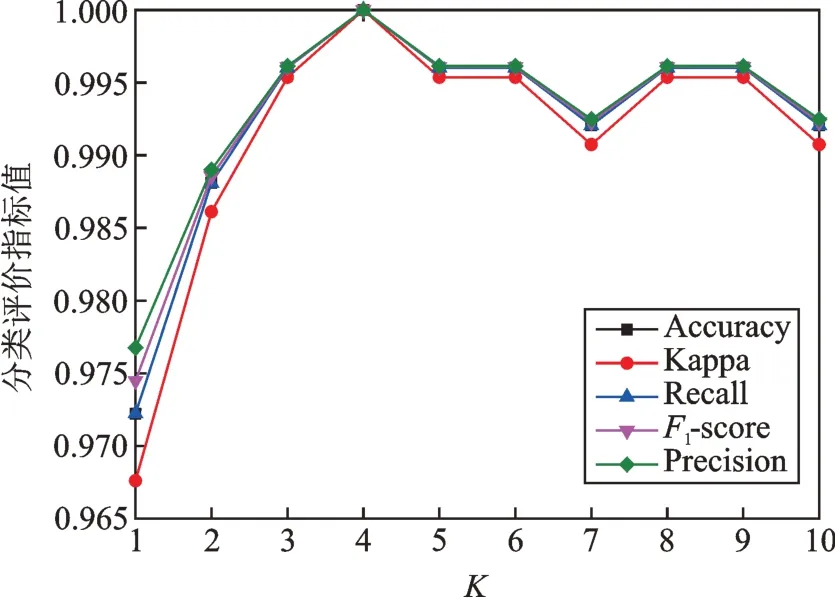
图7 不同K 的IDSMM 的五种指标对比Fig.7 Comparison of five indicators of IDSMM in different K

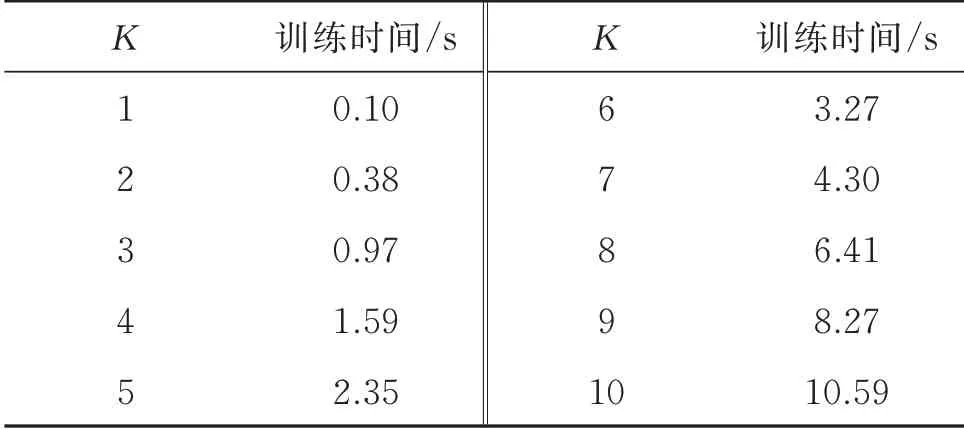
表6 不同K 的IDSMM 训练时间Tab.6 IDSMM training time in different K

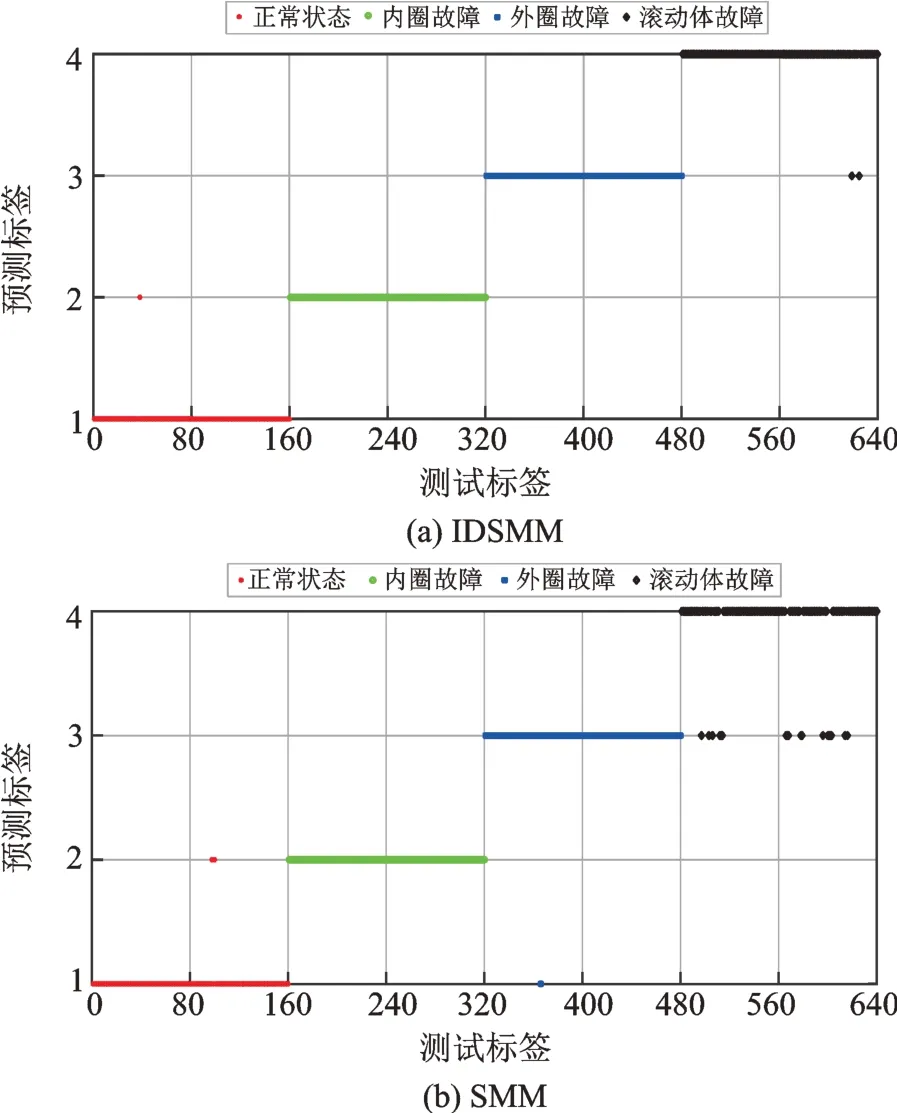
选择150 组样本作为训练集，剩余200 组作为测试集，分别使用五种方法进行实验，实验结果如表7、图8 和9所示。从表7 和图8 中可以看出，IDSMM 五种指标均高于SMM，RSMM，SSMM 和MRMLTSMM，再次证明了该方法有着良好的分类性能。图9 为根据分类结果得到的混淆矩阵。从图中可以清楚看出，在增加故障类别，提高数据复杂度后，IDSMM 存在较少的错分现象，但第1 类和第5类仍被全部正确区分。考虑到偶然因素的存在，再次选择350 组样本进行5 折交叉验证测试，图10 展示了五种方法在5 折交叉验证下的测试结果。从图中可以看出，IDSMM 方法具有较高的分类正确率，平均正确率可以达到99.80%，SMM，RSMM，SSMM 和MRMLTSMM 的平均分类正确率分别为97.43%，98.53%，99.14%和99.63%。相比其他四种方法，IDSMM 方法在5 次分类中的正确率均稳定在99%以上，识别效果最佳。究其原因在于，SMM利用输入的特征样本构建目标函数，特征数的增加对其模型的影响较大，使得分类准确率波动较大。SSMM 和RSMM 通过增加稀疏属性和约束使得模型具有鲁棒性以及冗余特征的抗干扰能力，但是，SSMM 和RSMM 本质上还是构造平行超平面，对复杂数据难以完成有效的样本分割。

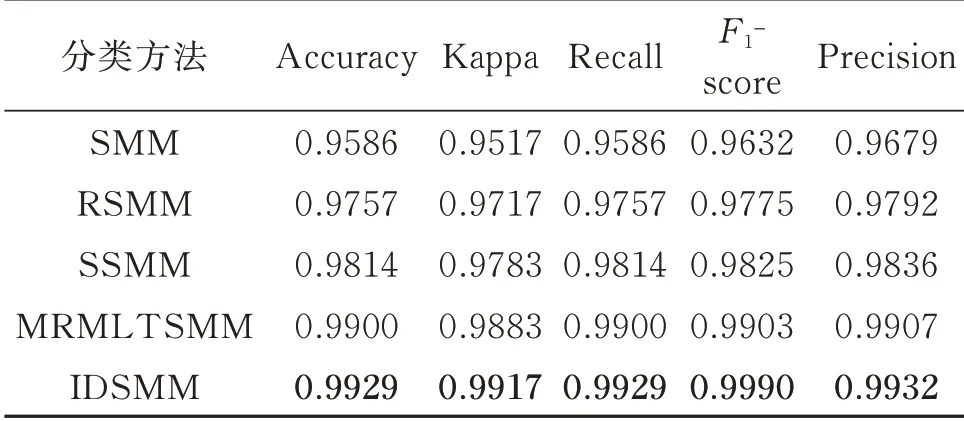
表7 五种方法的分类性能对比Tab.7 Comparison of classification performance of five methods

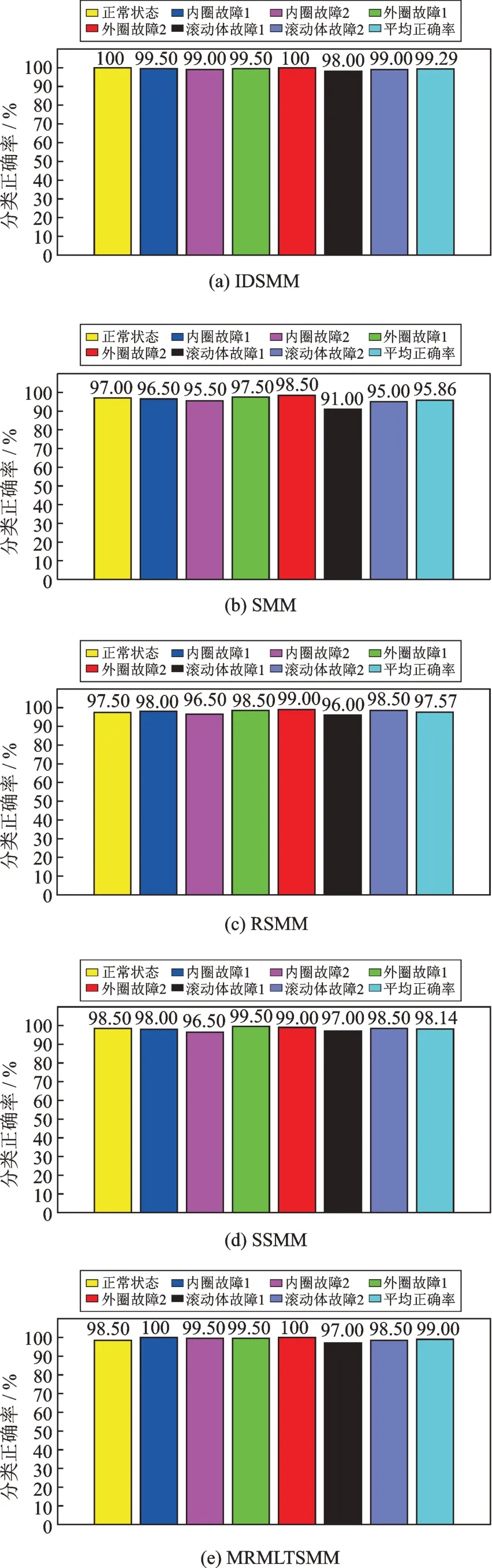
图8 五种方法的分类结果Fig.8 Classification results of the five methods

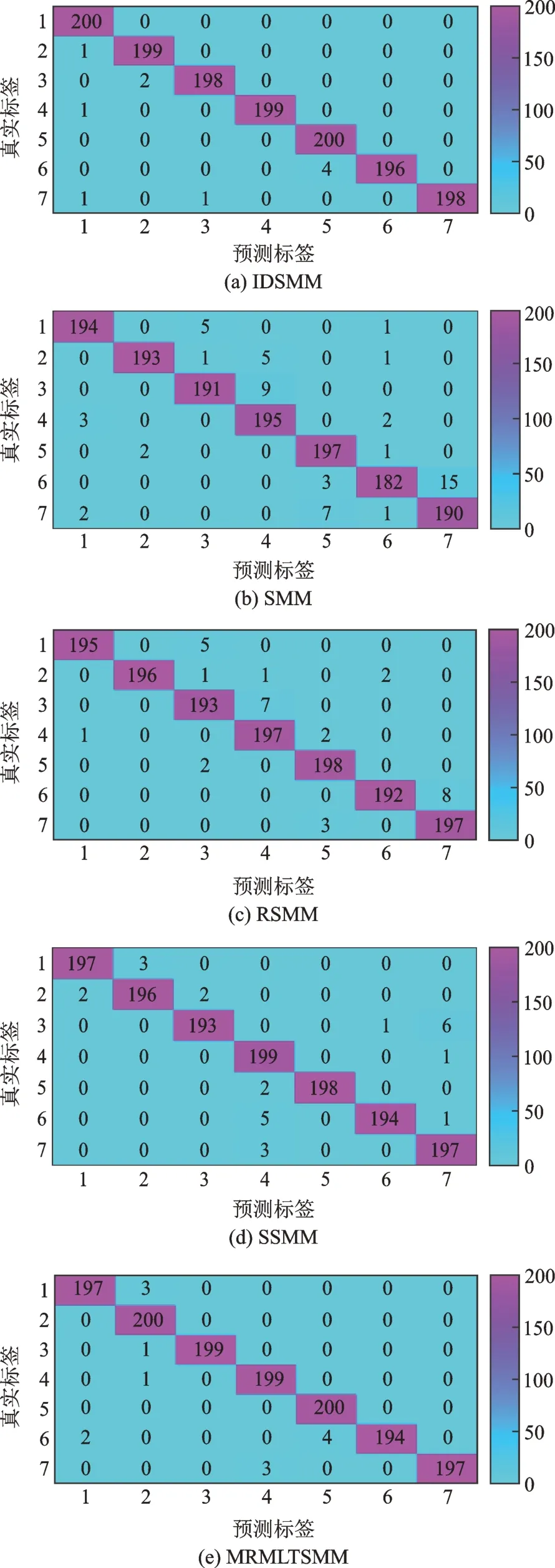
图9 五种方法的混淆矩阵Fig.9 Confusion matrix of five methods

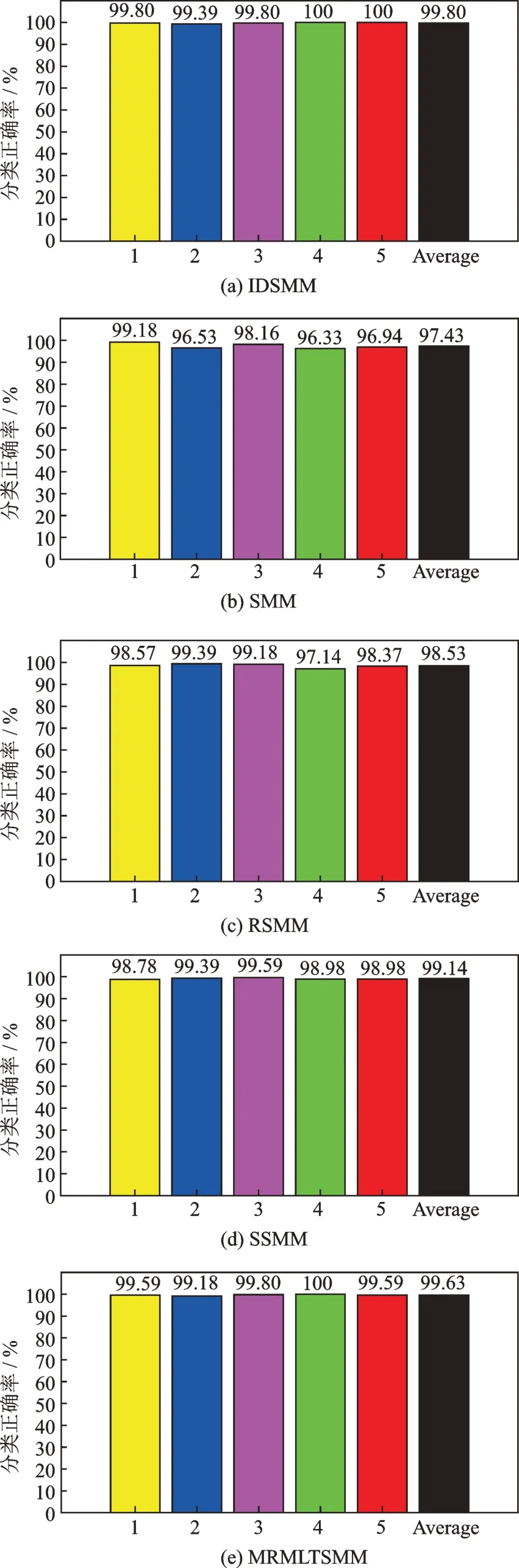
图10 5 折交叉验证五种方法的结果Fig.10 Results of five methods in 5-CV

为了判断IDSMM 方法的小样本分析能力，随机抽取10，20，30，40，50，60，70，80，90，100 个样本作为训练样本，150 个测试样本。IDSMM，SMM，RSMM，SSMM 和MRMLTSMM 五种方法得分类结果如图11所示。从图11 中可以看出，IDSMM 和MRMLTSMM 方法都具有优异的小样本数据分析能力，当训练样本数为10～40 时，IDSMM 分类正确率比MRMLTSMM 略高。总的来说，无论训练样本数多少，IDSMM 和MRMLTSMM 分类准确率都高于其他三种方法。SSMM 和RSMM 的识别性能低于IDSMM，但也表现出了良好的小样本分析能力。由于SMM 模型具有较差的鲁棒性和泛化能力，其在任一训练样本数下的分类正确率都比其他四种方法低，表明SMM 小样本分类性能最差。

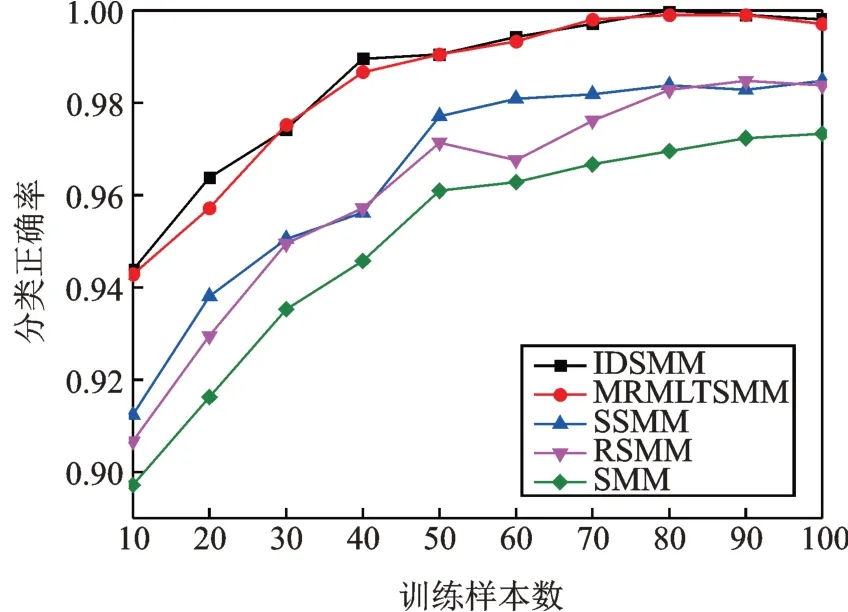
图11 不同训练样本数的分类正确率Fig.11 Classification accuracy of different numbers of training samples

综上所述，根据五种方法在5 种衡量指标下的对比结果可知，IDSMM 的诊断性能明显优于SMM，RSMM，SSMM 和MRMLTSMM。IDSMM采用一种交互偏移超平面的方式构造两个超平面，当数据较为复杂时，可以为每一类特征样本构造一类超平面。同时，由于本类样本所属平面与异类样本的距离被拉大，因此具有更好的分类性能。SMM作为一种平行超平面分类器，当输入数据包含多种特征信息时，其无法有效构造合适的超平面。SSMM 构建模型的前提是回归矩阵具有低秩特性，因此在面对大多数矩阵是多秩的情况下很难发挥模型本身的优势，而IDSMM 引入了左右多秩投影矩阵，可以更好地解决该问题。相比其他平行超平面分类器，IDSMM 因其借助NHC 思想构造超平面的方式，在处理二分类问题尤其是复杂问题时具有明显的优势。

3 结论

本文提出一种交互偏移支持矩阵机（IDSMM）的矩阵分类方法。不同于传统非平行超平面的构造形式，IDSMM 在建模过程中，在每个目标函数中加入偏移参数，以改变约束，构造出一对交互偏移超平面Tr(WT1X(1))+b1=1 和Tr(WT2X(2))+b2=-1。交互偏移超平面克服了复杂数据间的有效分割问题，并且每一个超平面距离异类样本更远，提高了模型的泛化能力。同时，IDSMM 使用左右投影矩阵构造目标函数，避免了数据过拟合问题。通过对两个滚动轴承数据集进行实验验证，实验结果表明，与SMM，RSMM，SSMM 和MRMLTSMM 相比，IDSMM 在滚动轴承故障诊断中具有更优异的性能。