双马达伺服系统改进PSO和ECF相结合同步控制

王飞飞，张 明，王 强3，

（1.新乡职业技术学院智能制造学院，河南新乡 453000；2.河南理工大学机械工程学院，河南郑州 451460；3.洛阳市华冠齿轮股份有限公司设计部，河南洛阳 471131）

随着电液伺服系统应用领域的不断推广，要求仿真转台进一步提升控制性能，双马达控制可实现同步驱动效果［1-4］。考虑到在系统中同时设置两组阀控马达系统时难以实现对运动参数的同步协调控制功能，极大增加了液压马达输出结果的偏差。在承受负载作用下运行时，不能实现同步对称控制的效果，会造成同步控制精度的明显下降［5-6］。

王晓晶等［7］通过分析电液伺服系统的运行控制过程，加入预测函数滑模变结构控制方法，有效提升了伺服系统的运行控制精度。粒子群算法可以实现良好的鲁棒性，且该算法计算过程简单以及能够满足快速收敛的要求［8-9］。Wu 等［10］以粒子群算法与遗传算法相结合的方式实现交叉运算，根据验证分析结果判断，采用改进粒子群算法处理非线性系统之后能够准确整定PID 参数。郑宇等［11］通过构建仿真模型测试了转台外框在双马达结构下的同步控制性能，在此基础上开发出了一种具备变惯量自适应的鲁棒同步控制方法，实现了对双马达精确位置控制与跟踪的效果；之后结合仿真测试数据，可以判断以上方法可以实现理想控制性能。郭治富等［12］研究了双液压马达进行同步驱动过程中依然会出现不同步现象，并开展了深入分析，根据同步控制效果可知，按照上述方式设计的控制器能够满足多种复杂工况下的高精度同步控制要求并获得良好鲁棒性。

根据上述文献报道可知，到目前为止对双液压马达开展同步控制都是按照马达形成的角度位移信号进行过程控制，并对各项参数进行调整。为达到更高精度，本文运用改进粒子群算法和反馈误差校共同实现的控制方法，最后通过测试发现该方法可以达到理想控制性能。

1 系统设计

1.1 双马达伺服系统

本文设计的仿真转台由机械结构、油源结构、电气结构、控制结构4 部分组成，属于立式结构的液压驱动平台系统。系统共包含了3 个框架，能够按照特定的运动形式控制负载所在的位置。系统动力通过双液压马达伺服系统提供，图1 给出了双伺服马达的结构示意图。本次设计的液压马达同步控制系统内共由2 组阀控马达组成［13］，阀芯位置利用设置相应输入电压的过程进行控制。按照以上控制模式来实现对电液伺服阀流量与油压的调节功能，确保液压马达输出轴能够实现角位置的精确调控功能。

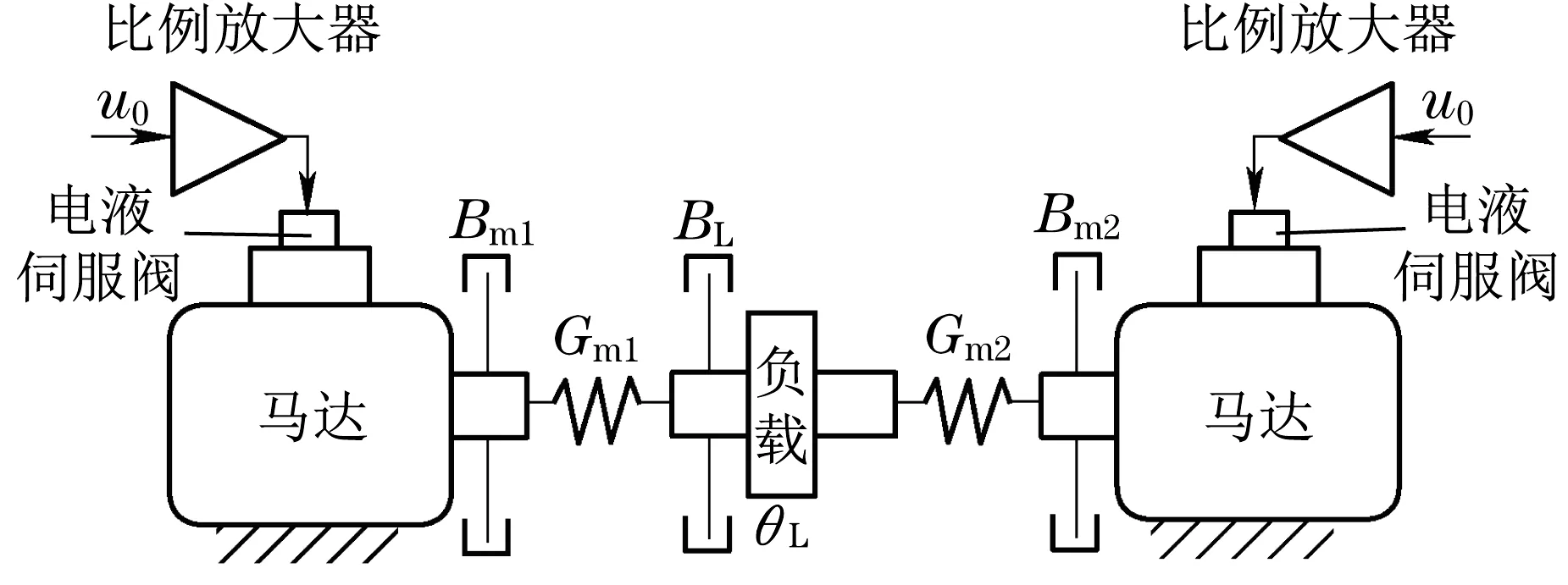
图1 双马达伺服系统结构Fig.1 Dual motor servo system structure drawing

1.2 数学方程

以下给出了电液伺服阀进行流量控制的线性方程［14］：

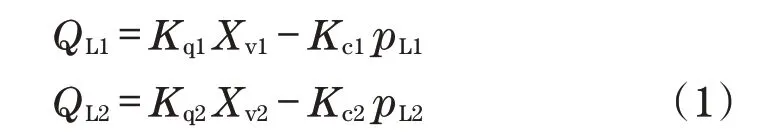
式中：QL1、QL2为两个液压马达对应的负载流量；Kq1、Kq2为伺服阀流量增益，可以通过控制阀芯在阀体的不同部位来获得相应的流量增益；Kc1、Kc2为伺服阀的流量压力系数；pL1、pL2为液压马达承受的负载。

为实现系统调控功能，采用液压伺服阀进行功率放大并对信号实施转换。结合本实验中设置的电液伺服阀条件，可将其作为2 阶振荡结构的形式。在不同流量下对应的伺服阀线圈电流计算式为

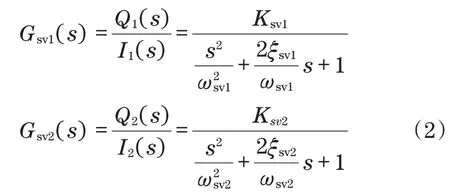
式中：ξsν1、ξsν2为伺服阀的阻尼系数。

考虑到电液伺服阀是以电流信号作为输入信号，在构建液压系统模型的时候，通过伺服放大器实现比例控制，传递表达式为

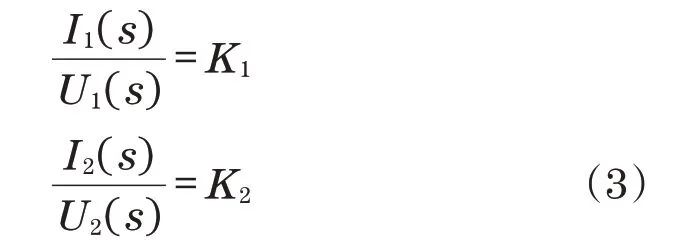
利用位移探测器采集负载转动角参数，再将角度信号传递到输入端，由此达到精确跟踪指令信号的效果。

2 控制设计

2.1 同步控制

液压同步闭环控制包括同等与主从控制两种模式，此外还可以同时利用以上两种同步控制方式组成新控制模式。例如，共反馈同步误差校正模式需要先计算主反馈误差，以此实现对跟踪误差进行调节的效果，同时利用同步误差补偿液压马达的控制偏差，使前后两个马达保持基本接近的输出结果，由此获得更精确的同步控制结果，最终实现运动控制效果的大幅提升。根据液压马达两腔压差为本文同步控制系统提供同步反馈信号，同步误差流程如图2所示。

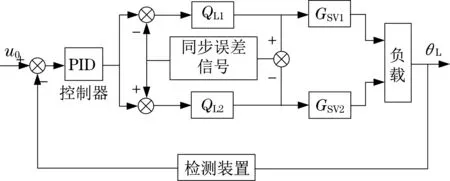
图2 同步误差流程Fig.2 Flow chart of synchronization error

2.2 改进粒子群优化算法

粒子群优化（particle swarm optimization，PSO）算法是根据鸟类捕食进行模拟得到的群体优化算法［15］。利用上述算法进行控制时，粒子往最优目标发生转移并进入最佳的适应值区间内。经过上述处理后，再按照个体和群体极值参数，对粒子运动速度与位置进行数据更新，具体计算式为

利用改进粒子群算法进行处理时，先计算粒子适应值，并根据该值优劣实施排序。去除低于平均适应值的粒子，再经过交叉计算获得优化粒子，经过扩展后粒子群达到最初的数量，对应的位置计算如下：

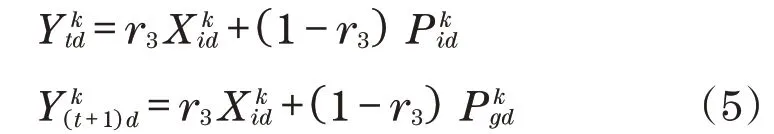
式中：Ytd为以交叉操作方式获得的新粒子d维位置；r3取值位于［0，1］之间。

对粒子进行变异计算时，持续优化粒子适应值的过程中，形成了更小的变异概率。再为粒子各维位置从［0，1］区间中选择一个随机数。对于粒子第d维Xid随机数小于粒子变异概率时，则按照以下式子完成Xid的变异操作：

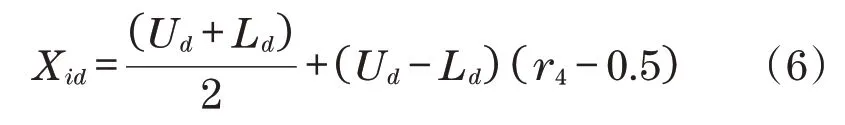
式中：r4为［0，1］区间中的一个随机数。

以改进粒子群算法得到最优PID 参数，实现了系统动态控制性能优化的效果并显著提升同步控制精度。以下为PID控制器表达式：

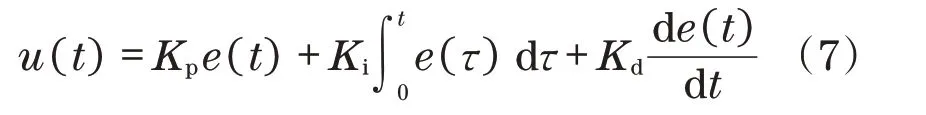
粒子位置维度都被包含在PID 内。以下给出了按照ITAE指标进行粒子适应度计算的过程：

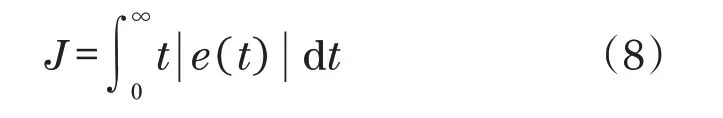
3 仿真结果分析

为实现液压马达控制系统性能进行综合评价，设定左、右马达的黏性阻尼系数后，同时使左电液伺服阀的偏差设定在+0.008。液压马达、伺服放大器、电液伺服阀的具体参数见表1。

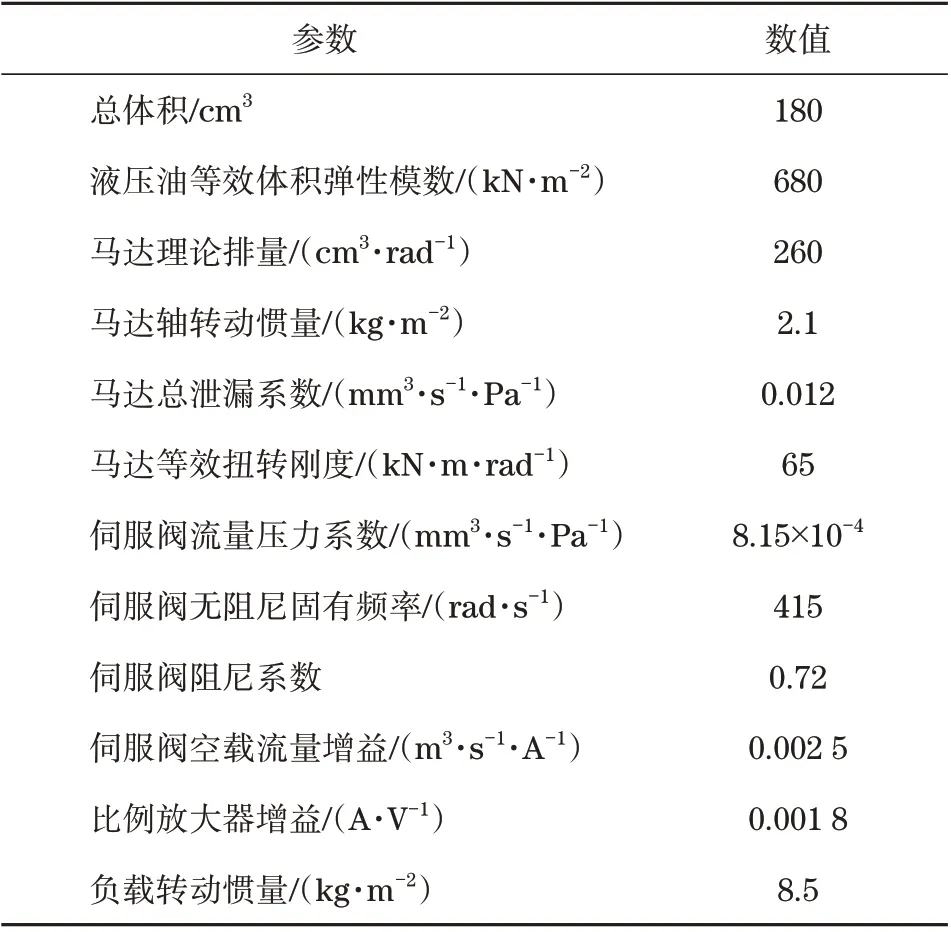
表1 模型参数Tab.1 Model parameters

先以粒子群算法调用Simulink模型，同时完成粒子所有维度位置的参数设置，再设置Ki、Kp、Kd评价指标判断模型控制效果。改进粒子群算法具体参数见表2。

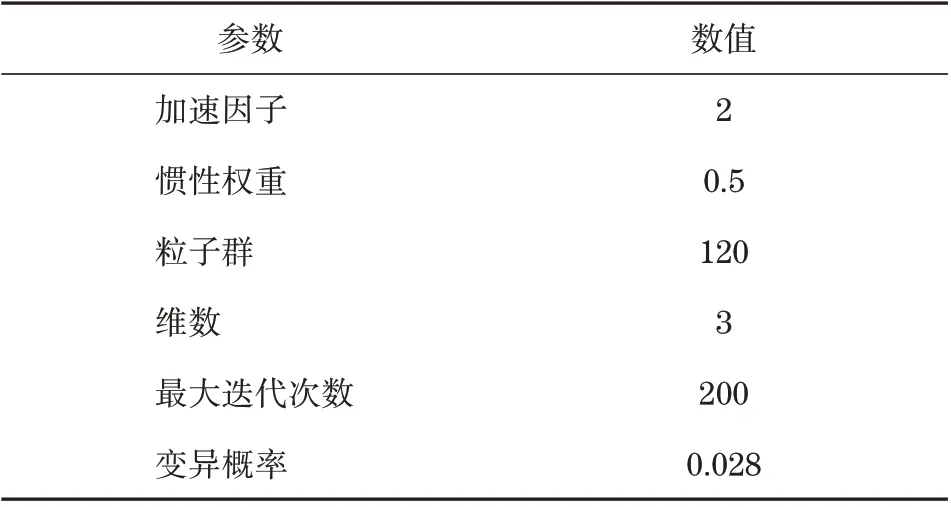
表2 算法参数表Tab.2 Parameter table of algorithm

在系统中输入阶跃信号后再对其瞬态响应性能进行测试。将系统同步反馈通道增益设置成0.001，通过仿真测试得到结果如图3所示。

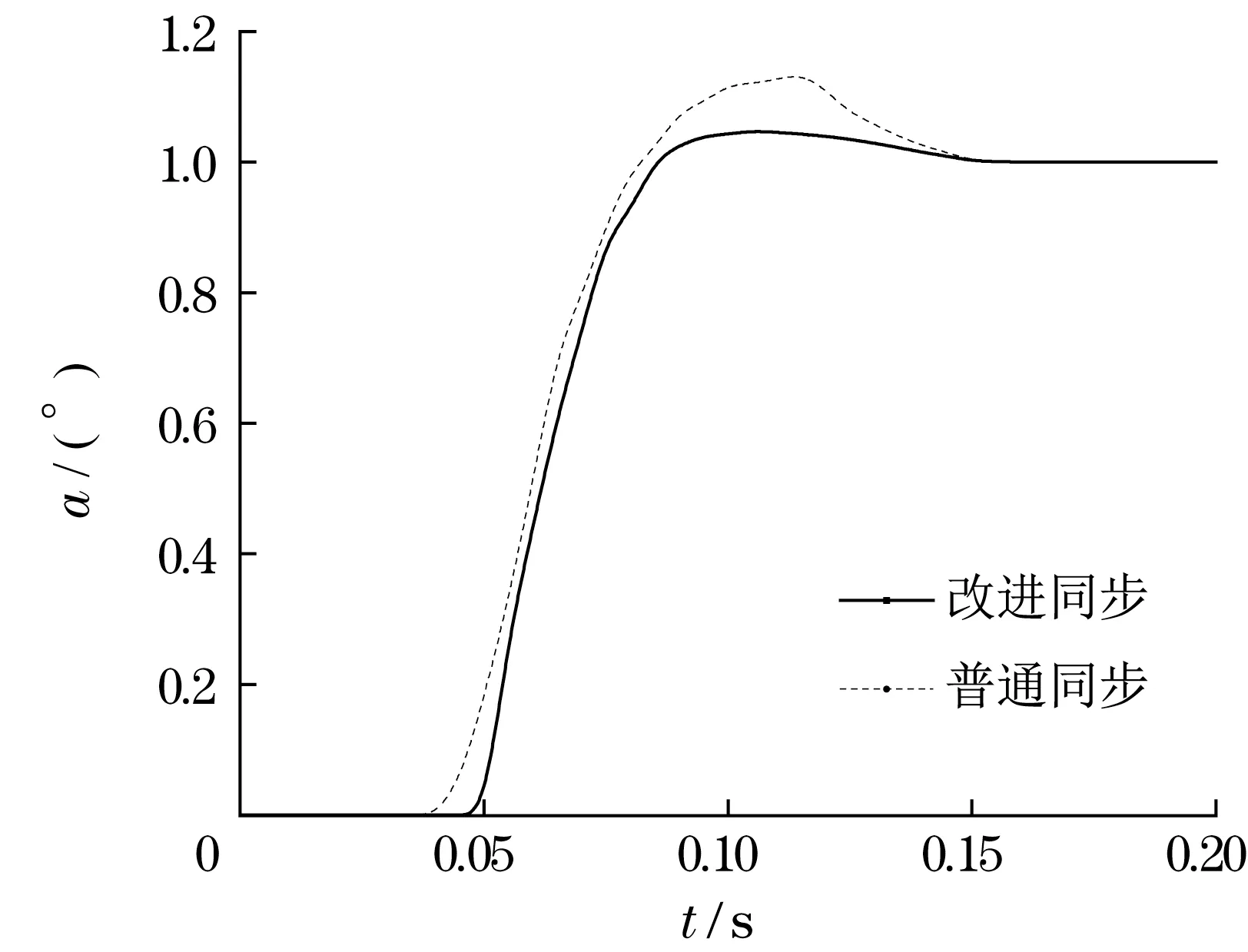
图3 系统阶跃响应曲线Fig.3 Step response curve of the system

系统响应性能的各项评价指标见表3。同步控制策略PID 依次为341.5、10.72 与45.32。融合了PSO 算法以及共反馈同步误差校正的PID 参数为301.3、0.107 2、41.04。采用改进后的PSO算法与共反馈同步误差校正得到的PID 参数分别为349.2、0.844 6、55.15。以上测试结果显示，利用改进后的复合控制方法可以显著降低系统超调幅度，并获得更小稳态误差。

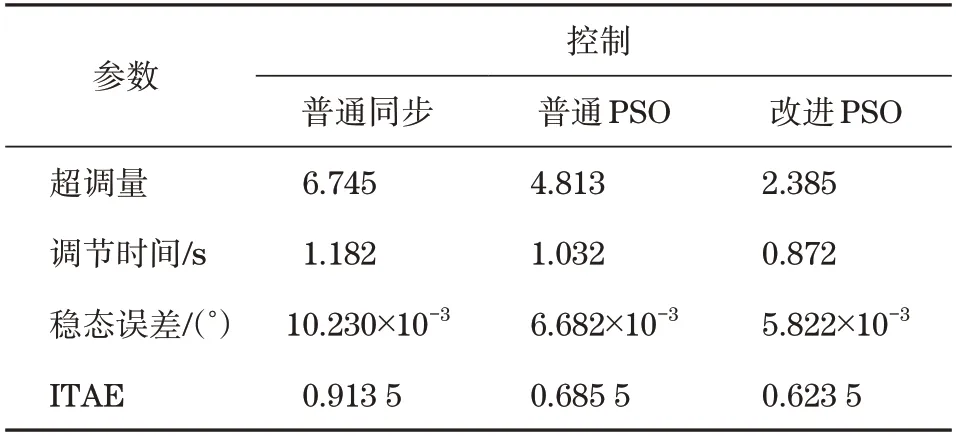
表3 系统响应指标Tab.3 System response index

图4 给出了设置正弦输入信号的情况下，以合适控制方案测试获得系统信号响应过程的角位移与跟踪误差。

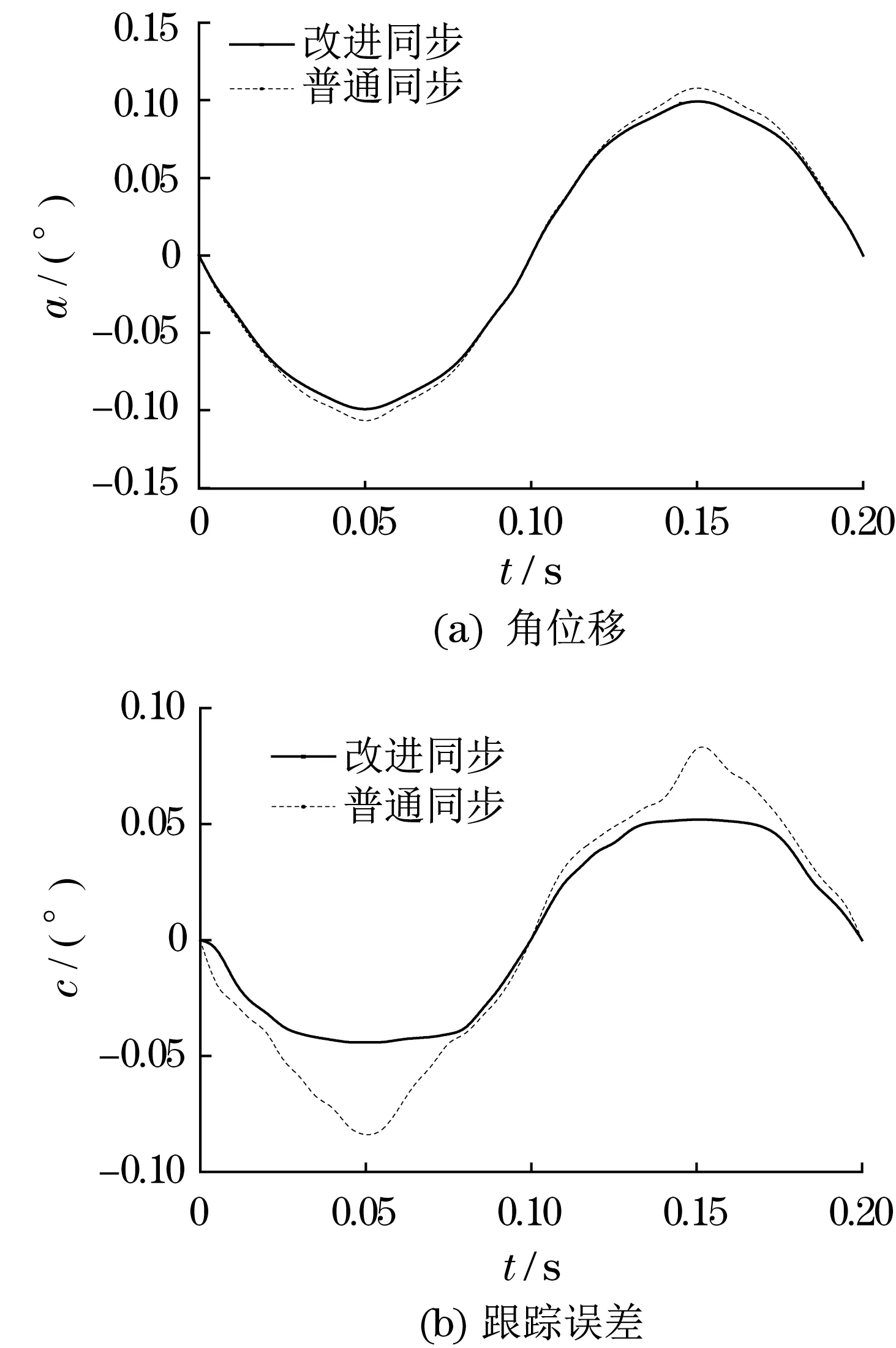
图4 正弦系统响应曲线Fig.4 Sinusoidal system response curve

利用系统处理正弦信号之后，再通过复合同步控制的方法使跟踪误差被控制在±0.1°范围内；经过优化处理的复合同步控制方式获得不超过±0.05°的跟踪误差。根据以上系统响应测试结果可以发现，经过共反馈同步误差校正，引入改进粒子群算法后使系统超调显著减小，并大幅降低了波动性，最终优化了系统控制性能。

4 结论

（1）在系统中输入阶跃信号后再对其瞬态响应性能进行测试。通过系统响应性能的各项评价指标得到：利用改进后的复合控制方法，可以显著降低系统超调幅度，并获得更小稳态误差。

（2）经过优化同步控制获得不超过±0.05°的跟踪误差。经过共反馈同步误差校正，引入改进粒子群算法后，使系统超调显著减小，并大幅降低了波动性，最终优化了系统控制性能。