基于DBN-PSO算法的钢板热轧轧机实时振动预测

钱素娟，张 伟，李 强

（1.郑州财经学院信息工程学院，河南郑州 450044；2.河南理工大学机械与动力工程学院，河南焦作 454000；3.河南富源机器制造有限公司设计部，河南郑州 450000）

对钢板进行轧制时，当热轧轧机发生剧烈振动时会引起轧件厚度偏差并形成表面微观裂痕。当产生瞬时剧烈振动时还会造成轧机零部件的损坏，因此需对轧机产生振动的原理与预防方案开展深入分析，这已经成为板带轧制领域的一项重点研究内容［1-3］。

轧机系统存在复杂的输入与输出关系，当其中一个输入量改变时可能引起多个输出发生改变，因此难以通过相同的振动理论对上述参数耦合关系进行分析，从而造成“幽灵式”振动的现象［4-6］。钢铁企业生产期间采集得到大量监测参数（real-time monitoring data，RMD），同时包含了轧机振动机理方面的运行规律，但会形成大量数据，并且参数和热轧轧机振动间存在复杂变化的关系，已经无法利用传统处理方式来处理这些庞大的数据，再挖掘得到可以准确反映轧机振动特征的特征参数［7-8］。孙明翰等［9］在轧机振动与非振动状态下进行7075铝合金板带铸轧的对比实验。基于振频、振幅对熔池区流场及温度场影响的不同规律，得出了振动铸轧工艺最优的振动参数为振幅0.56 mm、振频20 Hz。彭荣荣等［10］通过分析连轧时轧件受弹塑性形变的影响，且考虑相关振动参数和工艺参数，给出了一种具有滞后特性的轧制力表达式。分析了滞后振动系统的分岔行为，发现系统会随外扰力的变化在倍周期和混沌运动之间变换，有可能造成系统发生共振现象。

深度置信网络（deep belief networks，DBN）属于一类深度学习框架，可以有效满足数据分类与预测需求［12］。采用误差反向传播（BP）算法进行处理数据时，涉及信号正向传递以及误差反向传递过程，由此实现深度学习的功能［13］。本文利用RMD参数分析热轧轧机振动状态，综合运用DBN 与粒子群优化（particle swarm optimization，PSO）算法构建热轧轧机振动仿真模型，实现RMD 参数的深度挖掘，并达到热轧轧机振动的预测效果。采用现场测试得到结果对模型精度进行训练，同时利用该模型构建热轧轧机振动强度与轧制工艺参数定量关系，从而为优化轧制制度与轧制阶段达到快速减弱与去除热轧轧机振动的效果。

1 热轧轧机振动机理分析

1.1 热轧轧机振动模型建立

选择目前使用最普遍的集中质量法构建热轧轧机的振动仿真模型。根据热轧轧机特征与计算要求来设置简化热轧轧机系统，如图1 所示。图中：M1表示上横梁、机架立柱、压下装置等效质量；M2与M5依次表示上、下支撑辊系等效质量；M3与M4表示上、下工作辊等效质量；M6表示下横梁与垫块对应的等效质量；K1、C1、K7、C7依次为上部与下部支撑辊轴承座与上横梁间等效刚度与阻尼。

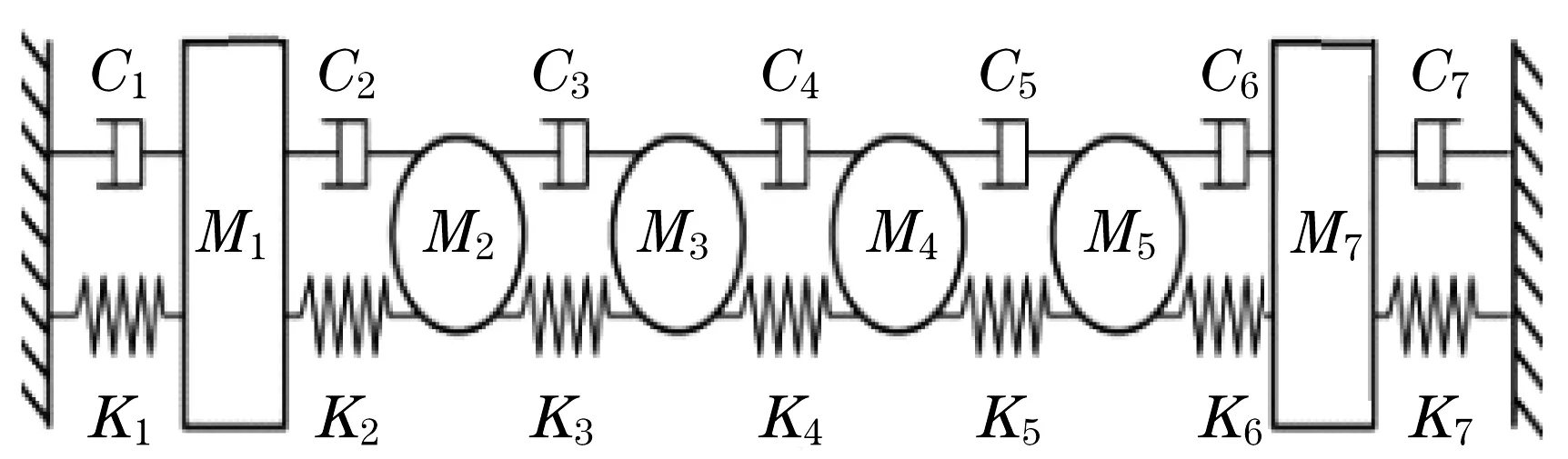
图1 热轧轧机振动模型Fig.1 Schematic diagram of vibration model of hot rolling mill

1.2 热轧轧机等效刚度和等效质量计算

本实验热轧轧机的各项性能参数指标见表1。当轧制阶段出现热轧轧机振动的情况时，可以认为此时动能与势能相等，把轧辊与机架按照梁结构进行处理，在全长范围内进行积分得到系统动能与势能最大值［14］。由此计算出系统各组成结构等效质量与刚度。

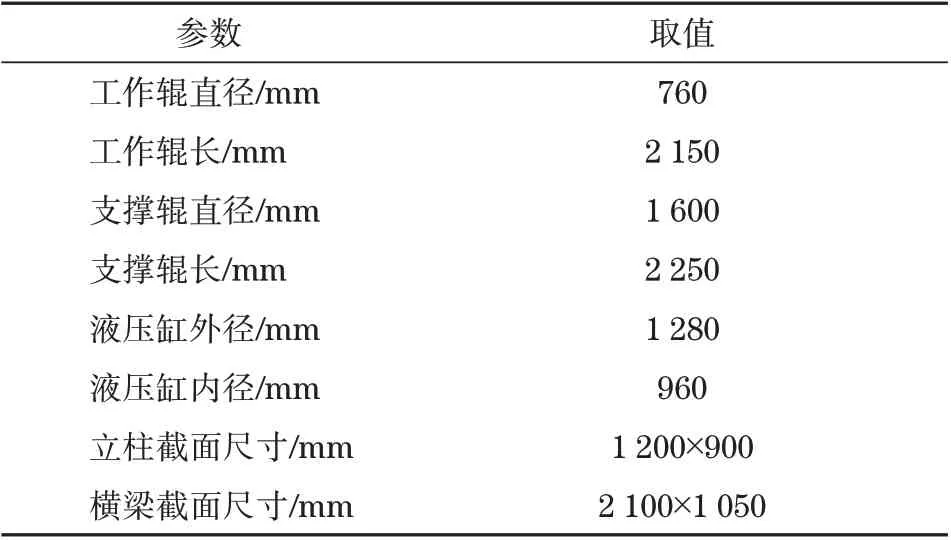
表1 热轧轧机主参数Tab.1 Main parameters of hot rolling mill

根据能量守恒原理，以Ki、Mi表示梁上i点的等效刚度与等效质量，Vmi、Ymi表示梁上i点的振动阶段速度与位移最大值，Tmi表示梁上i点的最大动能，ω表示振动圆频率，根据以下公式计算等效刚度Ki与等效质量Mi：

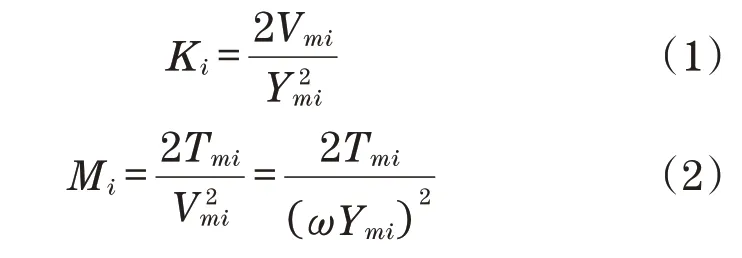
Ki与Mi计算结果见表2和表3。

表2 Ki值Tab.2 Ki valueGN/m

表3 Mi值Tab.3 Mi valuekg

采用ICP 压电加速度计测试热轧轧机机架沿垂直与水平方向的振动状态，结果显示当频率为160 Hz时沿垂直方向形成了最大幅度的振动，这跟本文分析结果相符，此频率属于3 倍频以内，对高速板带轧制过程造成了明显危害。

2 热轧轧机振动预测模型设计

2.1 DBN算法

热轧轧机振动过程属于多参数强耦合作用结果，需通过DBN 算法来实现数据样本的降维效果，由此提取得到本质特征参数，再将其输入PSO 算法中。

（1）采集原始数据。对轧制过程的轧制力、压下率、振动加速度、入口厚度、轧制速度、出口张力、入口张力、轧件宽度进行采集，以此作为输入量，同时输出热轧轧机振动加速度。

（2）输入数据归一化。通过prem 函数来完成对各项原始输入参数的归一化，得到原始数据区间为［-1，1］，如下所示：

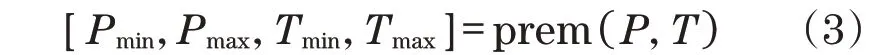
式中：P为初始输入数据；T为归一化处理所得结果。

（3）对样本进行聚类处理。聚类计算流程如图2 所示，聚类结束后再分析有效性，由此得到最优聚类数，本文选择离散型随机变量DB 指标进行分析［15］，根据如下公式计算得到DB：

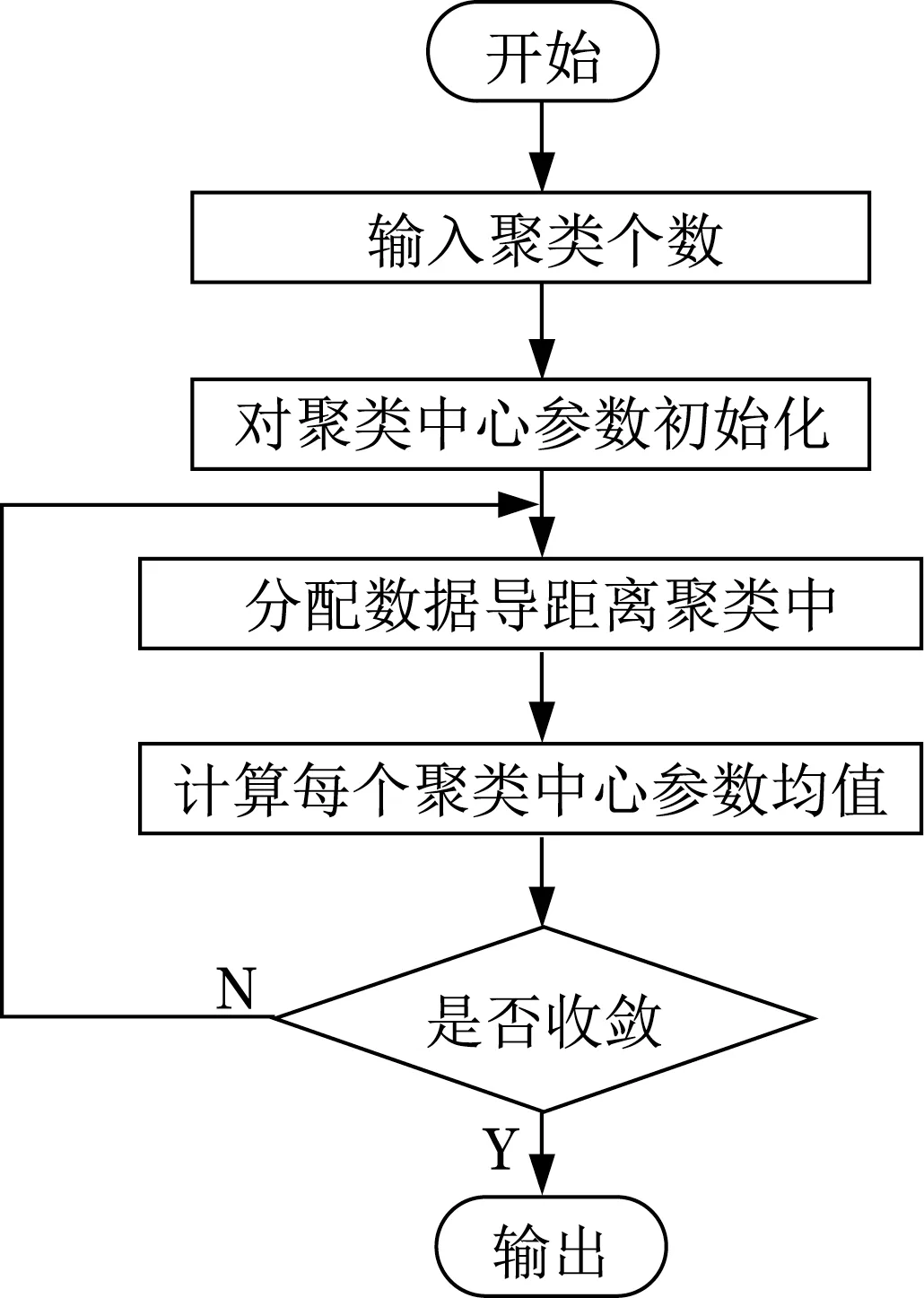
图2 聚类算法流程Fig.2 Flow chart of clustering algorithm

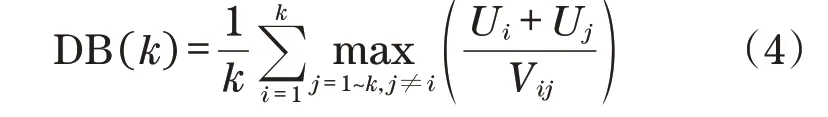
式中：K为聚类数，进行初始化处理时，为kmin、kmax；Ui作为Vi类离散数据均值；Vij为Vi类与Vj类中心均值；Uj为Vj类离散数据与聚类中心均值。

（4）对DBN 算法实施降维。按照DBN 算法原理实施调整优化，本文降维的处理过程见表4。

表4 降维处理参数选取Tab.4 Dimension reduction processing parameters selection

2.2 DBN算法相关性程度评价

为防止降维阶段造成数据特征丢失的问题，选择DBN 算法提取数据特征进行相关性评价，以P代表Pearson 相关系数，当P绝对值越大时说明相关性更强，结果见表5。

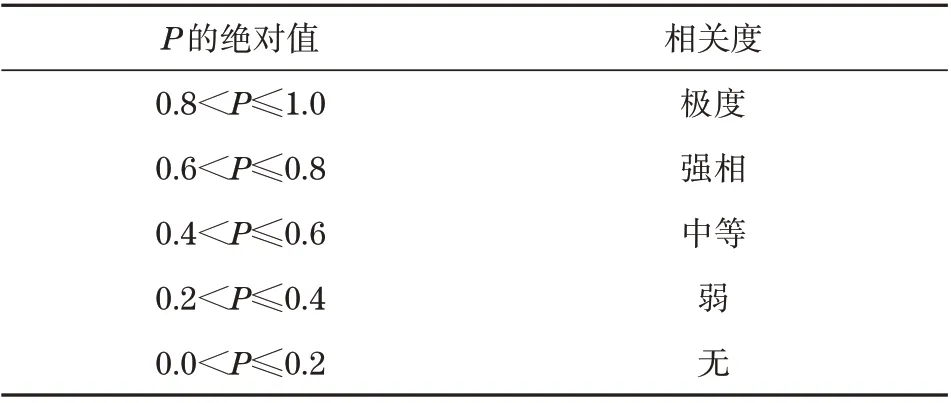
表5 相关性程度评价表Tab.5 Evaluation table of degree of correlation

从各类原始特征的每维特征中开展相关性分析，结果见表6。对第1 类数据样本进行分析，在1～5 维范围内，当维数增大后，形成了更高的相关性，1、6、9维属于极弱相关与无相关特征，其他各维达到中等程度或更高的状态；对于第2 类数据样本，介于1～5维范围内，当维数增大后，形成了更高的相关性，6、9 维属于无相关，1、2、7、8 属于弱相关，其余各维数据都达到中等或以上的相关程度；对第3 类数据样本进行分析，5～9 维属于极弱相关性或呈现无相关的特征，1、4 维属于弱相关性，2、3维属于中等相关程度。

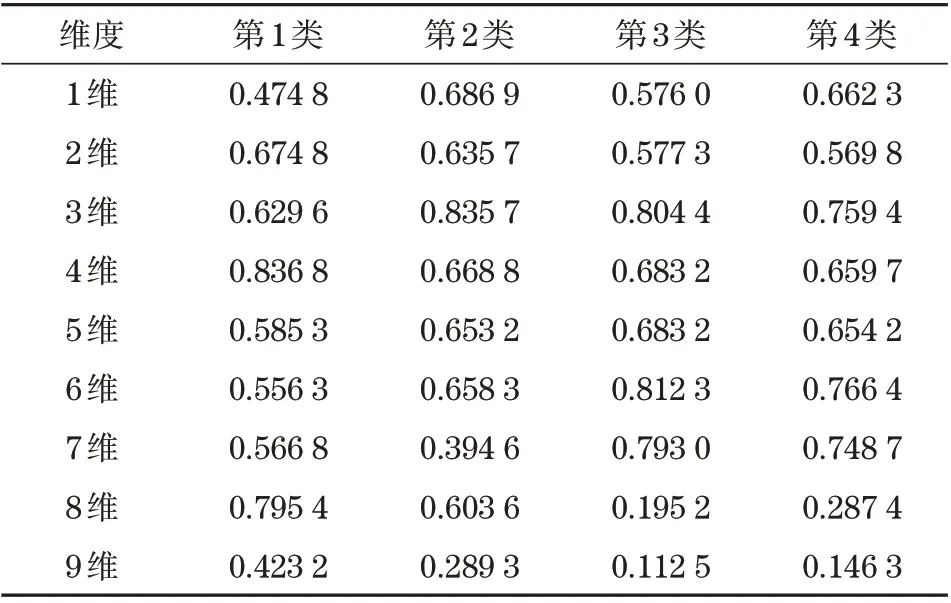
表6 4类原始特征相关性表Tab.6 Correlation table of fore types of original features

3 应用分析

以某热连轧生产线作为研究对象。当热连热轧轧机运行时，会引起热轧轧机机架的大幅振动，此外还会进一步造成热轧轧机轧辊以及分速箱齿轮发生表面结构磨损的问题。

利用本实验热轧轧机进行1.6 mm 厚度钢薄板轧制时引起的振动，从中采集得到轧制参数作为分析样本，总共包含200 组初始数据，本实验从中选择100 组数据样本训练预测模型，从而达到更高的振动预测精度，之后再对其他100 组数据实施预测，由此得到预测误差变化规律，根据以上结果构建不同轧制工艺参数下的振动强度关系。

3.1 振动预测模型诊断

选择预测值融合的方式对各隐层预测值进行初步处理，从而实现对DBN中包含的3个隐层降维特征通过PSO算法进行预测。结合对比所得结果，对本预测模型修正，经过多次处理直到预测结果形成与原始数据良好吻合状态。本模型预测结果如图3 所示。通过分析预测结果可知，第3 隐层则跟真实振动状态存在一定的差异性，经过融合可以使预测结果与实际振动状态达到相近结果。第2 与第3 类预测结果的隐层形成了与实际振动状态相近的预测结果，表现出了良好的预测性能。

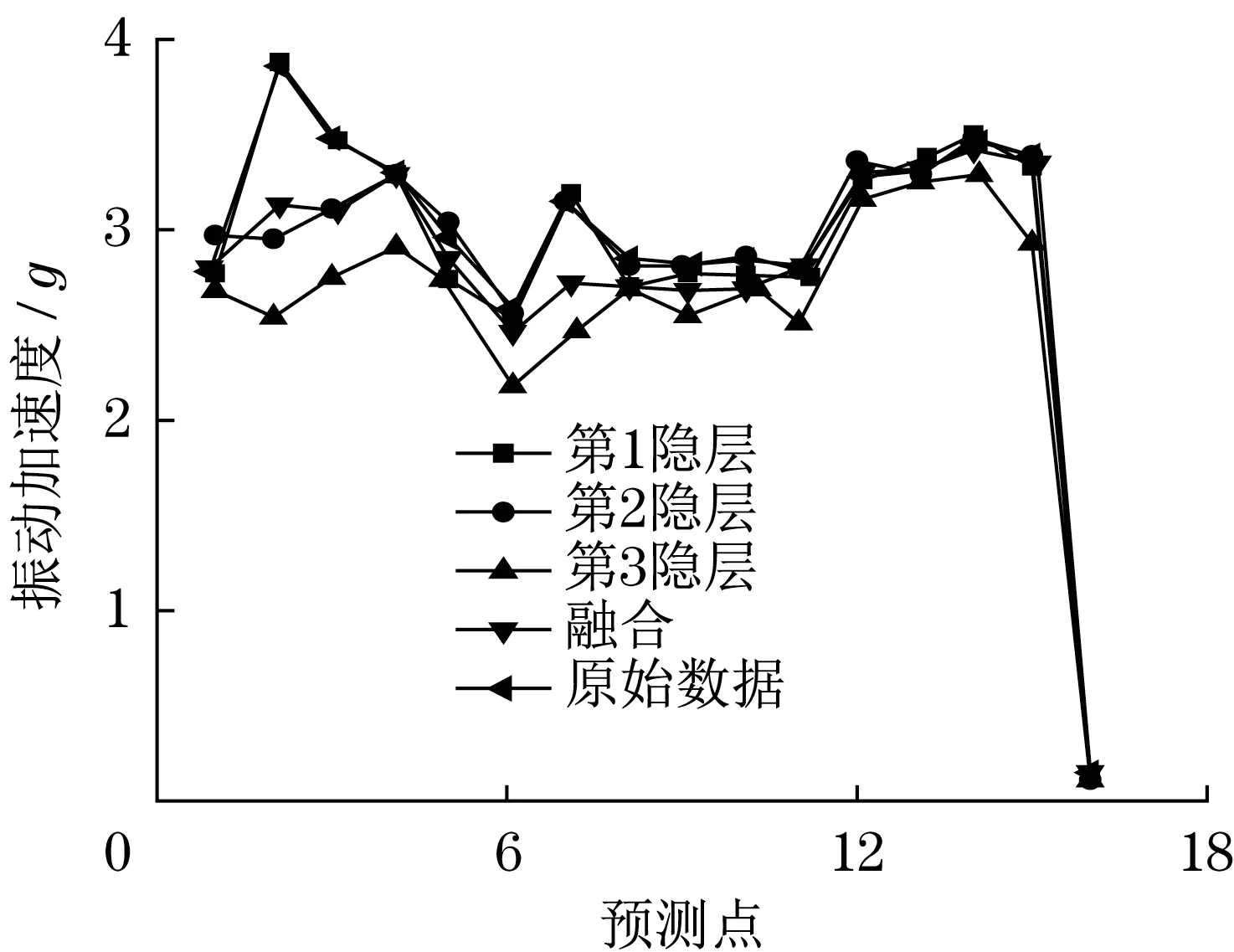
图3 振动预测模型诊断结果Fig.3 Diagnosis results of vibration prediction model

3.2 预测误差结果

为验证振动预测模型的预测准确程度，各项参数见表7。通过对比发现，预测误差不超过3.7%，达到了和热轧轧机振动状态良好吻合的状态。

表7 预测误差结果Tab.7 Prediction error result

3.3 不用轧制工艺下振动加速度预测

本文利用构建得到的振动预测模型研究了热轧轧机振动与各轧制工艺条件的关系。轧制工艺参数见表8。以本文振动预测模型进行分析时，设定各变量的单次变化幅度为5%，并控制其他各项变量恒定，以此研究轧制工艺参数和热轧轧机振动程度的定量变化过程，结果如图4所示。

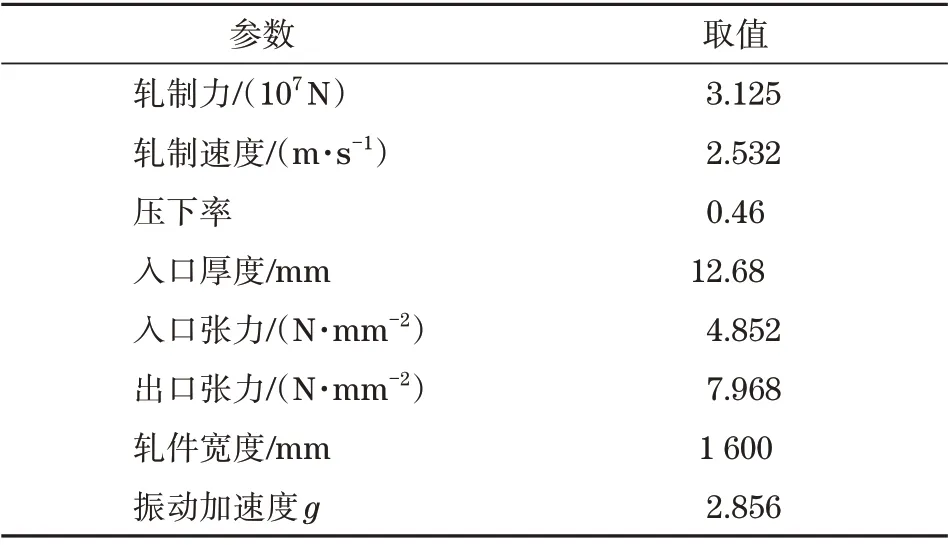
表8 轧制工艺参数Tab.8 Rolling process parameter

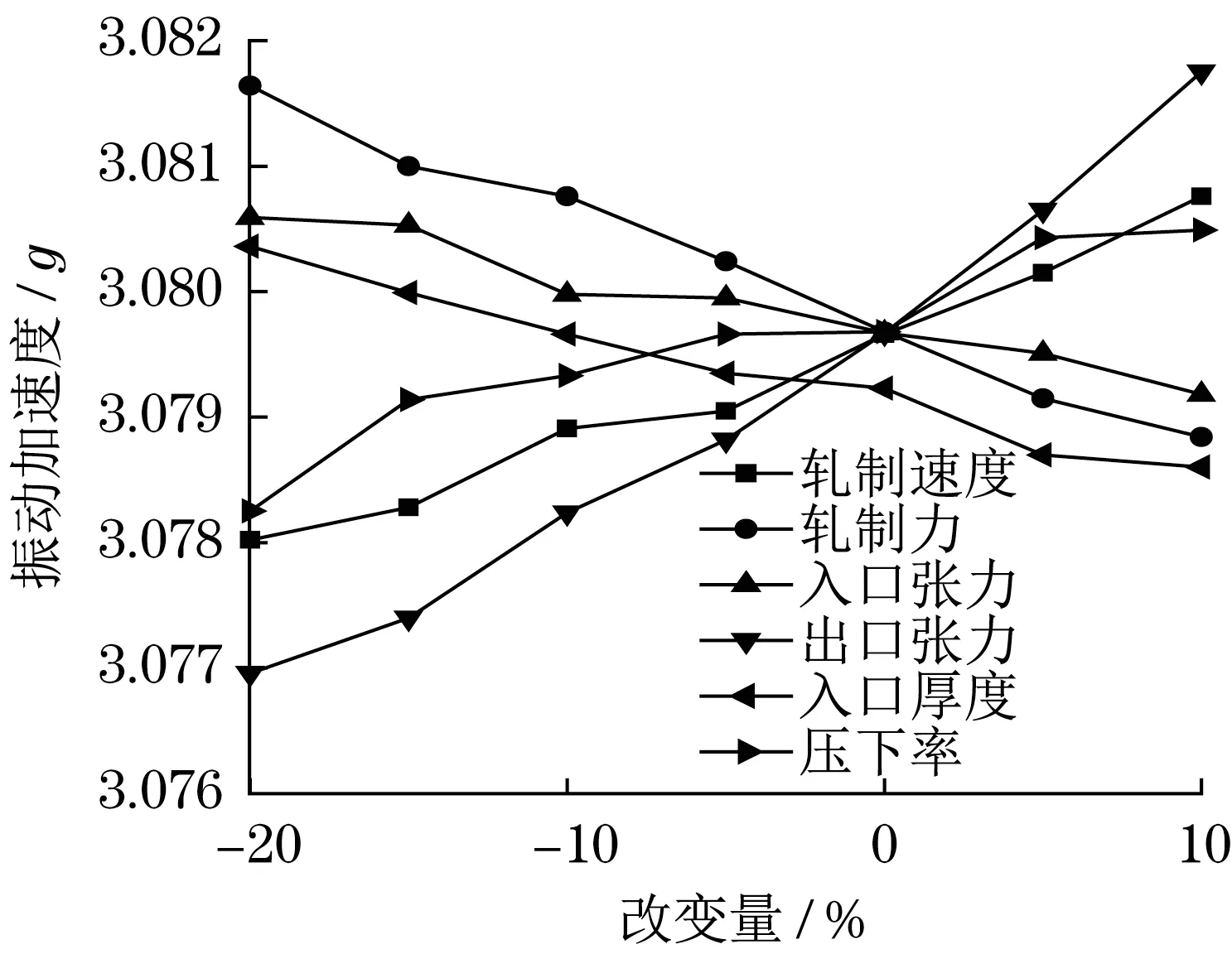
图4 不用轧制工艺下振动加速度预测结果Fig.4 Prediction results of vibration acceleration without rolling process

由图4 可知：逐渐降低轧制速度后，发生了热轧轧机振动加速度持续减小的趋势，当轧制速度降低比例达到20%时，对应的热轧轧机振动加速度降低了1.58×10-3g；当提高10%的轧制速度条件下，振动加速度升高了1.08×10-3g。不断降低轧制力的过程中，热轧轧机发生了振动加速度的持续升高，当轧制力降低比例达到20%时，振动加速度提高了2.02×10-3g；当轧制力提高10%时，振动加速度降低了0.93×10-3g。同时发现，当降低入口张力时，引起热轧轧机振动加速度的明显增大现象，入口张力降低20%后，引起热轧轧机振动加速度提高0.92×10-3g；当入口张力提高10%时，对应的振动加速度下降了0.48×10-3g。热轧轧机振动加速度与出口张力之间呈正相关变化特征，当出口张力降低20%时，对应的振动加速度降低2.74×10-3g；当出口张力提高10%时，振动加速度升高了2.09×10-3g。轧件宽度并不会引起热轧轧机振动加速度的明显改变，随着轧件宽度由1 100 mm 增大至1 700 mm 时，热轧轧机振动加速度最大与最小值相差1.3×10-3g。降低入口厚度后，发生了热轧轧机振动加速度的持续增大，当入口厚度降低20%后，振动加速度提高了0.71×10-3g。

结果显示，振动加速度主要受到轧制速度、出口张力、轧制力、压下率的明显影响。

4 结论

（1）通过对比发现，热轧轧机振动预测模型预测误差不超过3.7%，达到了和热轧轧机振动状态良好吻合的状态。

（2）逐渐降低轧制速度后，热轧轧机振动加速度持续减小，当轧制速度降低达到20%时，热轧轧机振动加速度降低了1.58×10-3g。热轧轧机振动加速度与出口张力之间呈正相关变化特征，当出口张力降低20%时，对应的振动加速度降低2.74×10-3g。降低入口厚度后，发生了热轧轧机振动加速度的持续增大，当入口厚度降低20%后，振动加速度提高0.71×10-3g。