基于运动学、刚度和动力学性能的并联机构有序递进三级优化设计及其应用
2022-07-25王一熙沈惠平吴广磊
王一熙 沈惠平 陈 谱 吴广磊
1.常州大学现代机构学研究中心,常州,2131642.大连理工大学机械工程学院,大连,116024
0 引言
并联机构的拓扑结构优化是指在满足机构基本功能(自由度、输出运动类型和数目)的情况下,优化机构的拓扑结构[1-5],但目前对并联机构拓扑结构优化的研究还较少,检索到的关于拓扑优化的论文大多是关于连续体的柔顺机构结构件的形状优化设计[6-7]。并联机构的尺度参数优化一直作为提高并联机构性能的主要手段[8-9],而目前并联机构的性能评价主要有三类性能指标,即机构的运动学性能、静态性能和动态性能[10-11]。
运动学性能评价主要依据基于工作空间、基于无奇异、基于转动能力的方向工作空间和灵巧度工作空间的性能指标来分别评价机构的运动/力传递性能、灵巧度和奇异性能[11];而静态和动态性能评价主要依据全局刚度、动力学灵巧度指标来分别评价并联机构的刚度、动力学方面的性能[3,10]。车林仙[12]利用带修复策略可行性规则的差分进化算法,对球面四杆机构函数进行综合,提出处理优化约束条件的可行性规则,其可靠性和稳健性指标优于对比算法;池腾腾[13]利用Isight和MATLAB软件的耦合分析,对2-RPU/SPR并联机构进行优化设计,并结合商用软件中的一些数值工具,较好地提高了优化过程的可重复性和稳健性;WU[1]运用NSGA-Ⅱ算法对3-RRR球面机构的运动学和动力学进行了多目标优化,通过Pareto前沿优化结果得到了两目标下球面机构的优化性能;吴超宇[14]采用权重系数,将Tripod并联机器人的运动学、动力学、刚度三者的多目标问题转化为单目标问题进行了优化;刘平松[15]基于工作空间大小、速度灵巧度和静刚度指标,对I4R型并联机器人全域性能进行了多目标优化;ALTUZARRA等[16]将线性驱动的四自由度并联操作手的工作空间体积和灵活性作为目标函数进行多目标优化设计;TAGHVAEIPOUR等[17]提出了McGill SMG并联机器人的多目标优化设计,旨在最大化机器人的工作空间和刚度,但使用的刚度指标无法充分代表刚度性能;WU等[18]通过预先确定的工作空间,对Ragar机器人运动学、静力学和动力学同时进行多目标优化,利用遗传算法给出了三目标下的Pareto前沿优化结果。CHE[19]用输入传递和输出传递两个指标来评价4-RUPaR并联机构的运动和力传递性能,并使其传递位置空间最大。
上述研究中还存在以下问题:机构优化设计的参数较单一,无法涵盖并联机器人运动学、刚度、动力学的全部设计参数;多目标优化时,较多的综合性能指标无法清晰地判断各自参数对整个优化过程的效果。
本文主要研究机构的综合参数优化,包括机构的尺度、截面及质量参数,即从并联机构产品设计的视角出发,在其初期设计阶段,提出基于运动学、刚度和动力学性能的有序递进三级优化设计策略和方法,也就是说为满足运动学层面的性能,首先优化机构的尺度参数以满足机构的工作空间体积、转动能力和运动/力传递性能;然后在已优化的尺度参数上,优化杆件的截面参数,使机构的刚度性能达到优化;最后,在已优化的尺度参数和截面参数的基础上,再优化杆件的质量(分布)参数,使机构的动力学性能达到优化。以文献[20]提出的零耦合度且运动解耦的2-(RPa3R)3R机构的并联操作为例,阐述上述综合优化方法及其求解过程。
1 2-(RPa3R)3R并联操作手
零耦合度且运动解耦的四自由度三平移一转动(3T1R)2-(RPa3R)3R并联操作手[20]如图1所示。该机构的动平台1及静平台0由两条相同的混合支链(HSOC)相连,每条混合支链由一个子并联机构和子串SOC{-R∥R⊥R-}(例:R22∥R23∥R24)串联得到,子并联机构是由与静平台0通过R11副相连的子串SOC{-R11∥R12⊥R13-}和子串SOC{-R21-Pa4s-}并联得到,其中,Pa4s为由4个球副(如S1、S2、S3、S4)组成的平行四边形(Pa)结构,子串SOC{-R22∥R23⊥R24-}的R22副串接在Pa4s结构的短边上,两条混合支链通过R24、R34与动平台1相连,且R24∥R34。
2 运动学尺度参数的优化
2.1 参数化建模
图1c为2-(RPa3R)3R并联机构的运动建模简图。静坐标系OXYZ的原点O为静平台重心,X轴正向垂直于转动副R41(A4)的轴线并指向其运动副中心,而Y轴正向平行于转动副R41的轴线并指向转动副R11(A1)的中心;在动平台1上建立动坐标系PX′Y′Z′,P为动平台中心,Y′轴正向垂直于转动副R24的轴线并指向其运动副中心,Z′轴和Z轴姿态相同,X′轴由右手法则确定。

(a)机构三维CAD图
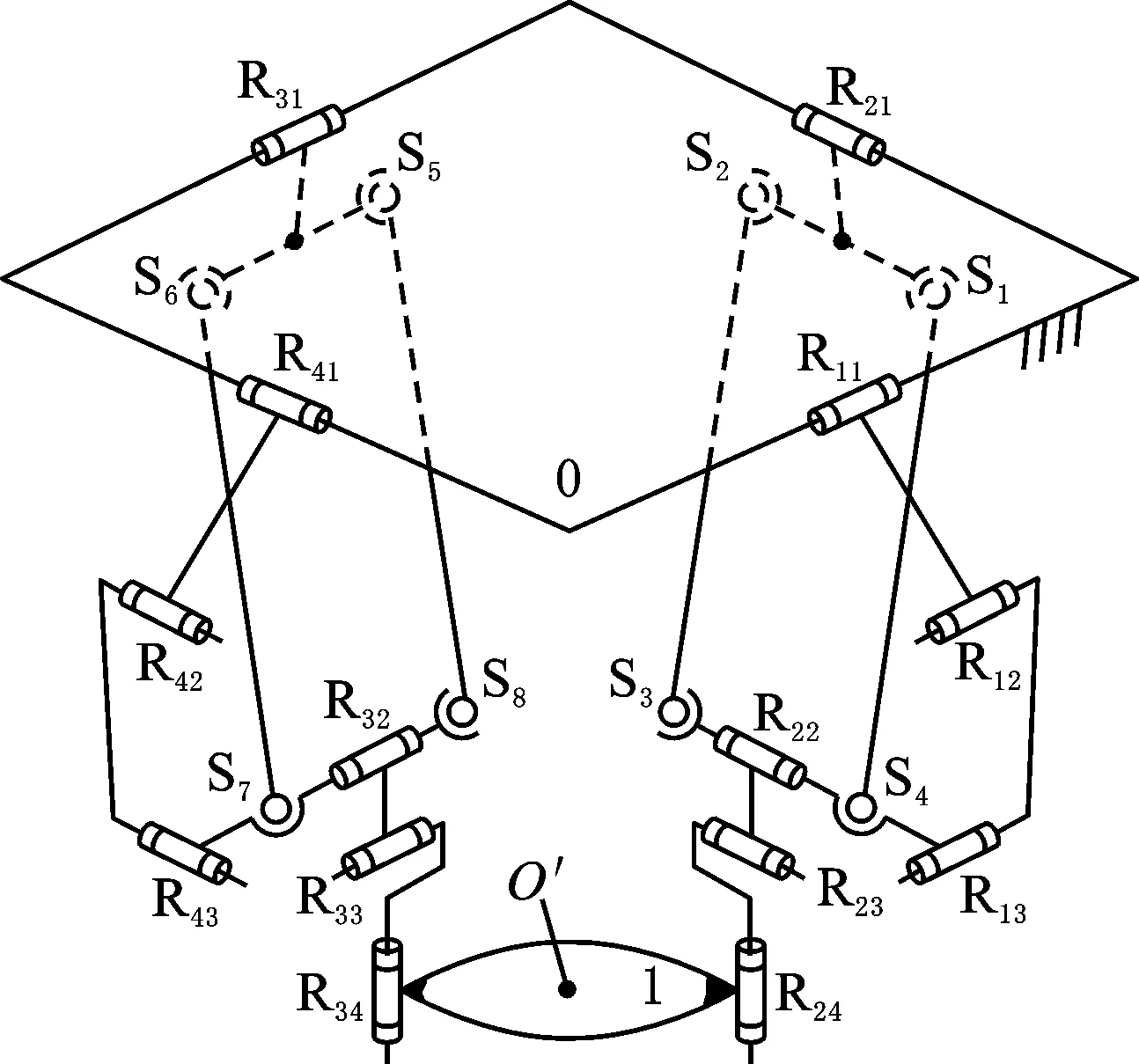
(b)机构运动简图
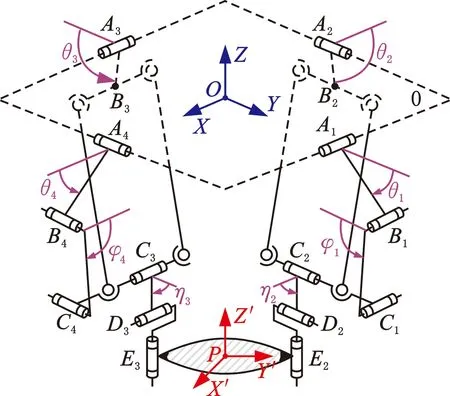
(c)运动学建模图图1 零耦合度且运动解耦的四自由度三平移一转动(3T1R)2-(RPa3R)3R并联操作手Fig.1 A 4-DOF(3T1R) 2-(RPa3R)3R parallel manipulator with zero-coupling and decoupling motion
定义I、J、K为静坐标系X轴、Y轴和Z轴的方向向量。各运动副中心分别记为Ai、Bi、Ci(i=1,2,3,4)和Di、Ei(i=2,3);在静坐标系中,它们相应的位置向量分别记为Ai、Bi、Ci和Di、Ei,符号标注如图1c所示。
在静平台0上,各驱动副中心的位置为
(1)
式中,la为驱动副Ri1到静坐标系原点O的长度;ai为驱动副Ri1中心Ai在静坐标系OXY平面的单位向量;R(Z)为绕静坐标系Z轴的旋转矩阵;I为单位阵。
四条支链中驱动副Ri1的轴线方向为
(2)
式中,ei为Ri1轴线在静坐标系中的方向向量。
驱动臂末端Bi的位置向量可表示为
Bi=Ai+lbbi
(3)
式中,lb为驱动副中心Ai和运动副中心Bi间的长度;R(X)为绕静坐标系X轴的旋转矩阵;bi为沿AiBi在静坐标系中的方向向量;θi为驱动副Ri1的转角,如图1c所示。
则子动平台1上各运动副中心的位置为
Ci=Bi+lcci
(4)
式中,lc为运动副中心Bi和Ci间的长度;ci为沿BiCi在静坐标系中的方向向量。
Ci(i=2,3)也可表示为
(5)

在6R空间结构(R22∥R23⊥R24∥R34⊥R33∥R32)中,位置向量Di和Ei可分别表示为
Di=Ci+lddi
(6)
ld=CiDi
Ei=Di-leK
(7)
le=DiEi
式中,di为沿CiDi的方向向量;ηi为转动副Ri3的转角。
进一步,可得动平台中心的位置向量为
P=Ei+lppii=2,3
(8)
lp=PEii=2,3
式中,pi为沿EiP方向的向量;α为动平台绕Z轴的顺时针夹角。
于是,末端的动平台1的中心位姿可表示为χ=[PTα]T。
2.2 逆向运动学
由文献[20]可知,2个子动平台(杆件S3S4,S7S8)均做二维移动,其运动平面始终垂直于驱动副Ri1(i=1,4)的轴线,得到Ci(i=2,3)的约束方程:
(9)
由式(9)可得
i=2,3
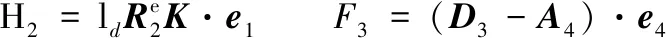
再利用几何约束条件建立约束方程,得
(10)
求得四个驱动副转角为
θi=
2.3 运动学性能指标
2.3.1可达工作空间
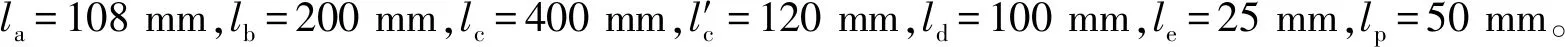
运用离散化方法[21-22],基于逆向运动学,取搜索步距为1 cm,可得到该并联操作手的近似于柱状的可达工作空间[23],它可认为是由无数个1 cm3的小立方体组成的三维体。因原始尺度参数下点集的数量为35 181,故可近似估计原始工作空间的体积V=35 181×1 cm3=35 181 cm3。据此,可将该工作空间体积定义为可达工作空间性能指标fv=V。
2.3.2转角工作空间
转角工作空间是指在动平台位置固定时,机构所能达到的所有姿态。SCARA并联操作手具有独立的一维转动自由度,转角工作空间是其重要的运动学性能,但动平台处于某一位置时,其转角只能在一定范围[αmin,αmax]变化,结合原始操作手尺度参数,得到操作手可达工作空间中z=-450 mm平面上的转动范围,如图2所示。图中等高线上的数值分别表示动平台在该区域内运动时,可达到的最小转角αmin和最大转角αmax。
但为统一评价机构在工作空间内的转动性能,定义Δα=αmax-αmin为单个位置下转角范围的大小,并用它来评价该位置下的转动性能,得到该机构在上述平面内Δα的变化情况,如图3所示。


(a)最大转角αmax
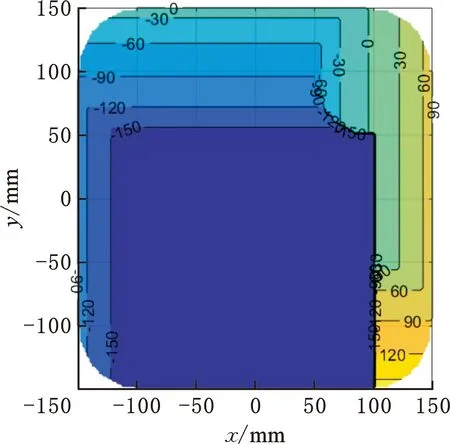
(b)最小转角αmin图2 z=-450 mm位置上的转角极值Fig.2 Extremum rotation angle at z=-450 mm

图3 工作平面中的转角范围Fig.3 Range of rotation angle at the working plane
2.3.3运动/力传递性能
机构的基本功能是实现从输入端到输出端的运动和力传递,现通过定义机构的全局传输性能指标来评估机构的传递性能[11,24]。
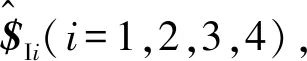
式中,“∘”为互易积符号。
为评价机构的整体输入传递性能,定义机构的输入传递指标为各支链中能效系数的最小值:
同样,通过运动旋量和力旋量的互易性,有
因机构整体的传递性能同时受输入传递性能和输出传递性能的影响,为评价机构整体的运动/力传递性能,定义机构局部传递指标(local transmission index,LTI)为机构的输入传递性能和输出传递性能中最差的部分,具体表示为
γL=min(γI,γO)
在该并联操作手的原始尺寸参数下,给出在定姿态时,工作高度z分别为-600 mm和-350 mm时局部传递指标的分布,其形状类似塔型,如图4a所示,而在多个不同姿态(转角为-90°,45°,180°)下,即动平台在静坐标系中的指标分布与定姿态相似,如图4b所示。
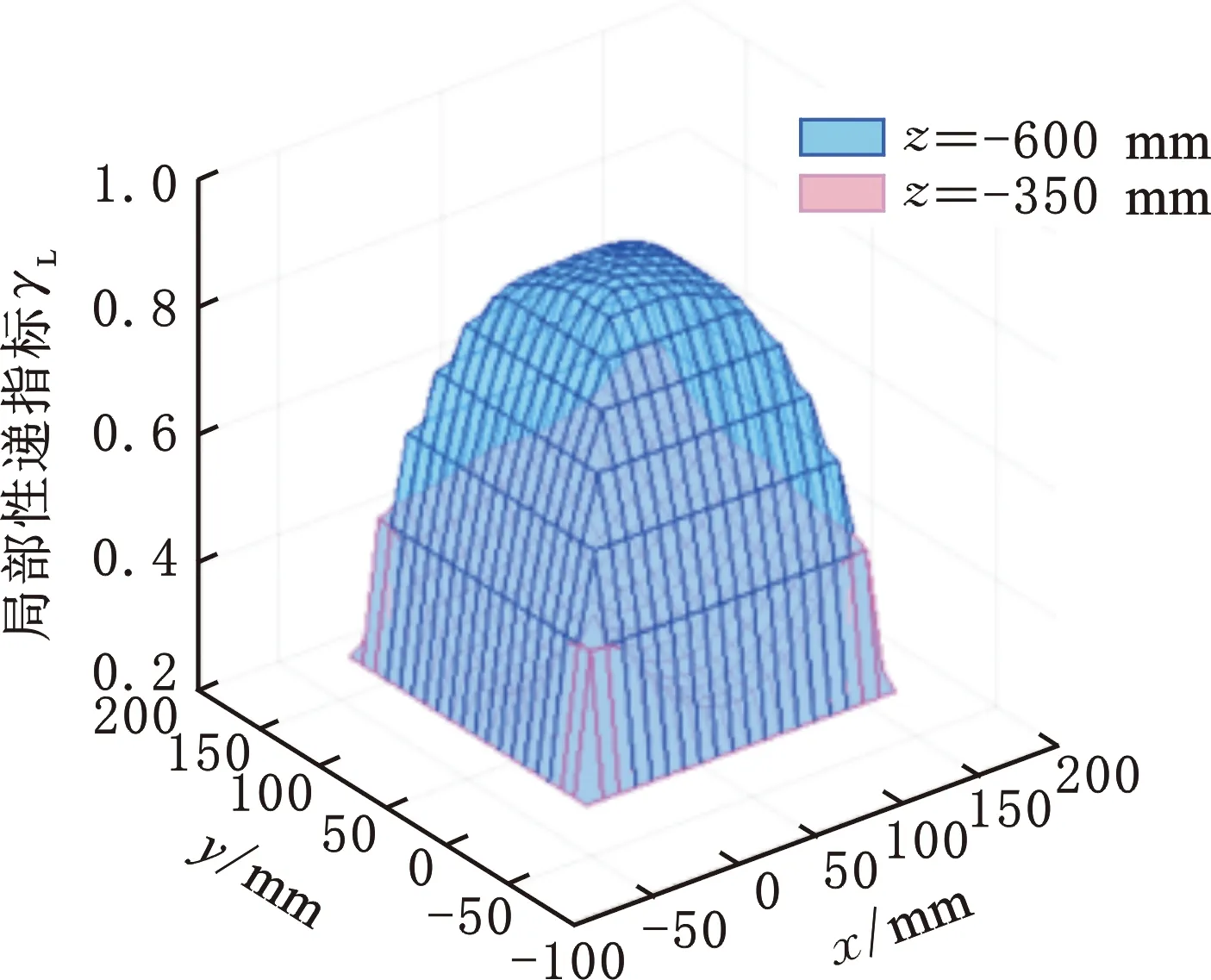
(a)不同高度z
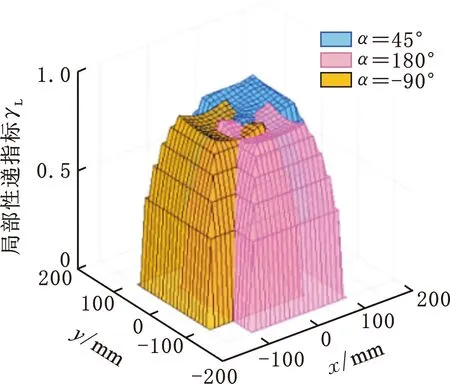
(b)不同姿态α图4 局部传递性能指标的变化Fig.4 Variation about local transmission index

2.4 基于智能优化算法的运动学性能优化
目前,智能优化算法主要有遗传算法(GA)、免疫算法(IA)、粒子群算法(PSO)、蚁群算法(ACO)、差分进化算法(DE)等[25],其中,GA、PSO、DE算法表现出很好的适用性和可靠性[26]。本文利用这三种智能算法进行计算,一方面,可将三个算法的优化过程和结果相互对比和验证,了解各自的优化进程及是否会陷入局部最优;另一方面,可比较分析这三种算法对并联机构优化设计的适用性和可靠性。
2.4.1确定尺度参数的约束条件
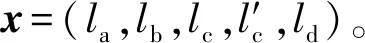
以原始尺度参数的±50%为设计变化量,确定设计变量的设计范围,如表1所示。

表1 尺度参数的设计变量及其变化范围
机构的可达工作空间受尺度参数的大小决定,因此,须对机构尺度参数的总和进行限制,由机构的原始参数,计算得
则在优化过程中,设计变量必须满足约束
关节的运动能力是并联操作手运动的基本保证,受结构和安装空间等因素的影响,考虑主动杆和静平台的干涉,确定驱动角的变化范围为θ∈(-78°,78°)[23];而对于平面四边形结构Pa4s而言,因长边杆和短边杆的相对运动存在运动干涉和限制,因此限制S副处的空间转角范围为(-60°,60°)[23]。
2.4.2确定目标函数
机构运动学性能的三个重要指标已在2.3节阐述,因此,可将工作空间(可达、转角)和运动/力传递的性能指标作为性能优化的目标函数,即
fV(x)=V(cm3)→max
于是,机构的运动学性能优化问题等效为对上述三个目标函数的加权优化问题[27]。由2.3节可知,该机构的工作空间形状规则,但可达工作空间较小,而机构的转角范围较大,因此,可适当提高可达工作空间的优化权重,这样,可将基于可达工作空间体积和运动/力传递的性能指标作为主要目标函数,分别得到50%和35%的权重,则转角工作空间性能指标为15%。进一步,为合理表达性能指标在优化过程中的变化,将各性能指标进行归一化,最终,得到的运动学多性能优化目标函数为
(11)
2.4.3优化过程分析和结果比较
对三种算法参数进行初始化设置[25],如表2所示。再借助MATLAB用三种算法分别进行优化计算,其优化过程如图5所示。从图5中可看出,随着迭代次数的增加,目标函数的变化趋向稳定值。将三种优化算法得到的尺度参数最优解、最优适应度函数fk及计算时间t进行比较,结果如表3所示。由图5可知,有限次迭代后,GA算法远未达到最优的目标函数值就已接近收敛;从优化效果(即fk值)来看,DE算法取得了最好的效果,PSO算法取得的优化效果与DE算法极为接近,但PSO算法用时较多。由图5和表3可知,在优化效果极为接近的情况下,DE算法与PSO算法得到的尺度参数有一定区别,PSO算法取了较大的la值和较小的lc值,DE算法与之相反,但DE算法的效果更优,说明PSO算法陷入了局部最优,也说明该机构运动学性能优化时存在相近峰值,但DE算法能更准确地得到最优解。
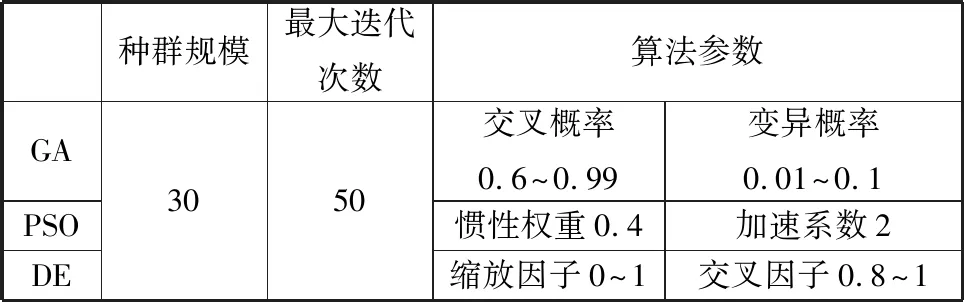
表2 智能算法的初始化
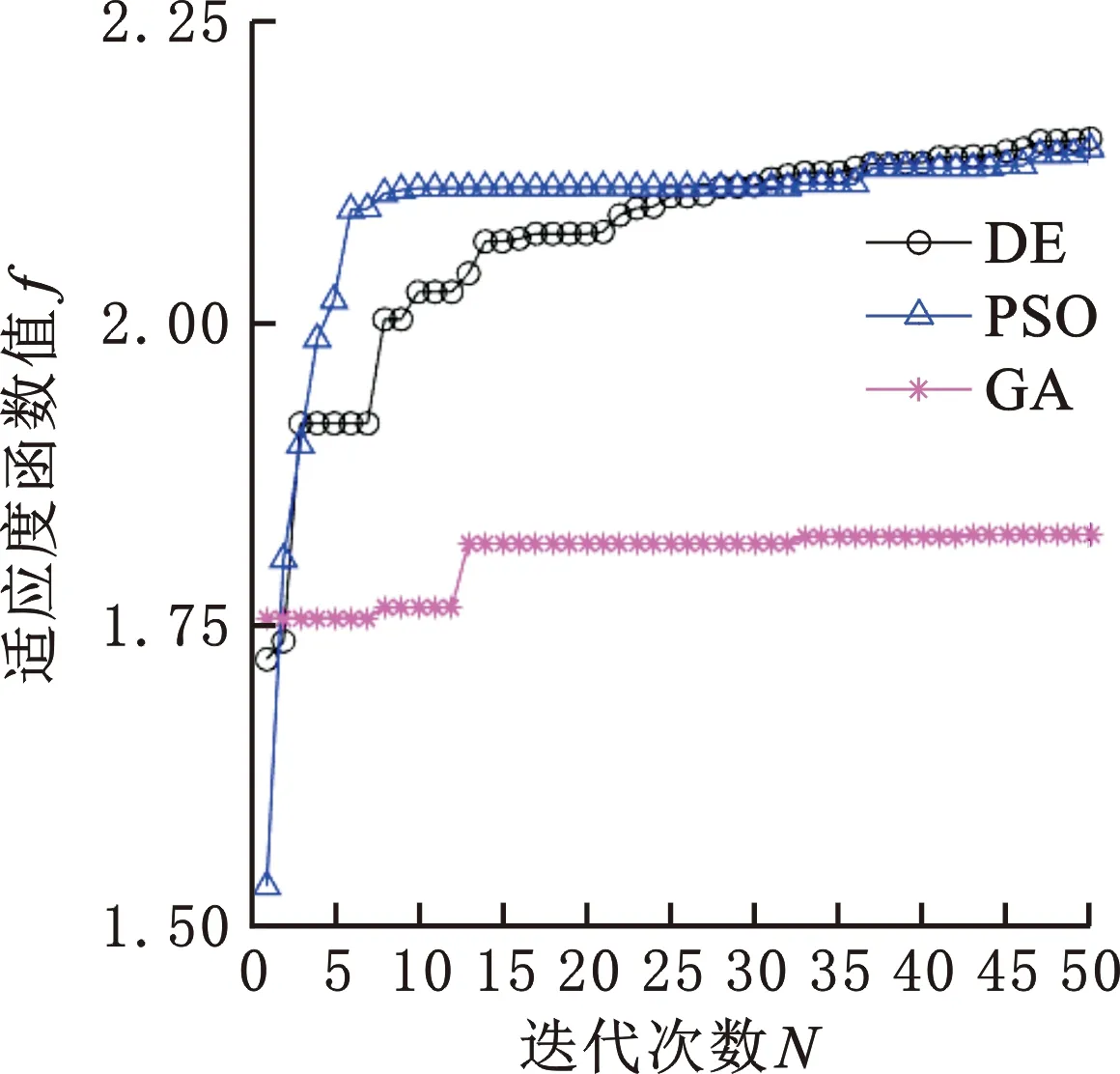
图5 尺度参数优化过程及其计算曲线Fig.5 Optimization process and calculation curve of dimension parameters
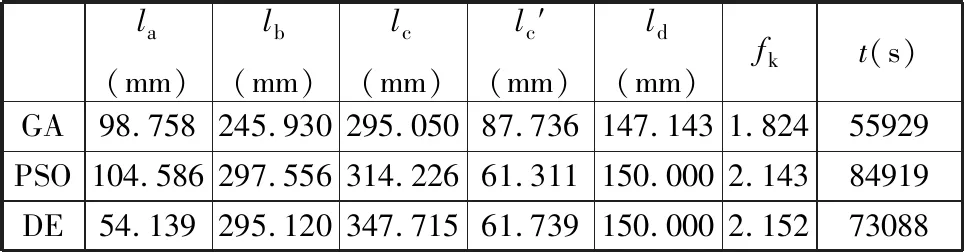
表3 优化前后的结构参数和最优适应度函数fk
将DE算法优化后的尺度参数进行圆整,以适应设计加工需要,并对比分析优化前后的运动学性能(工作空间、运动/力传递)指标,如表4所示。
由表4可知,优化后虽然机构的运动/力传递性能减弱了13.714%,但其可达工作空间的体积增加了233.282%,转角工作空间也增加了21.299%,如图6所示。

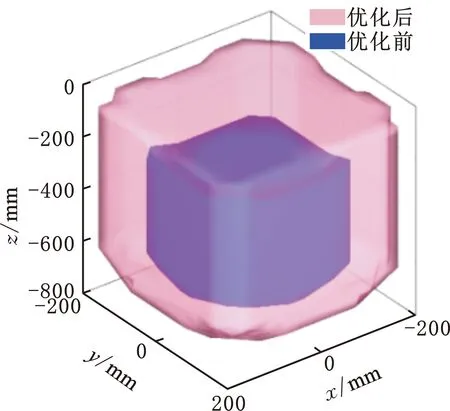
图6 优化前后的可达工作空间Fig.6 Reachable workspace before and after optimization
3 刚度截面参数的优化
3.1 刚度建模
并联机构的刚度是指动平台在外力作用下,因机构中弹性构件的变形而引起动平台产生微小位姿的难易程度。文献[28]提出虚拟弹簧法(virtual spring method,VSM),在不考虑预载荷的情况下,利用多自由度虚拟弹簧描述杆件在空间中多维弹性变形(扭转变形、弯曲变形和拉伸变形),并考虑杆件的拉伸/扭转变形之间的耦合特性;文献[29]利用旋量计算简化了该方法中运动映射的计算过程,可快速地对机构进行刚度建模分析与优化。本文采用VSM方法对2-(Pa3R)3R并联操作手进行刚度建模。因该并联机构是由两条混合支链组成的,因此先将每条混合支链分解为子并联机构和串联支链部分,并依次建立子并联机构、混合支链的柔性模型,然后,通过静力平衡方程得到支链的笛卡儿刚度矩阵,最后,将支链的刚度叠加,得到机构的整体刚度矩阵。
3.1.1分支链1、2的刚度矩阵

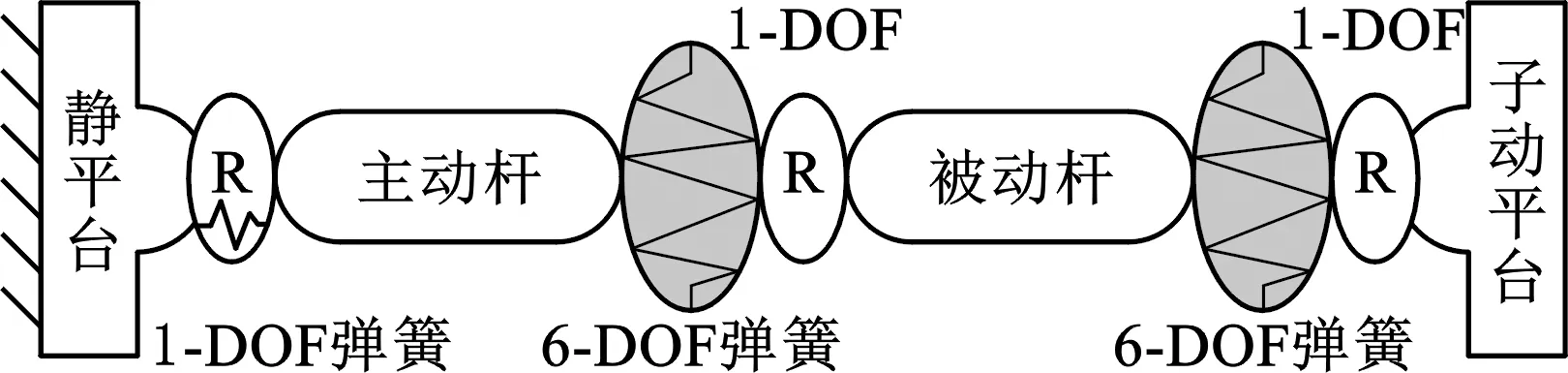
(a)R‖R‖R支链

(b)R-Pa4s支链图7 子并联机构中分支链的柔性模型Fig.7 Flexible model of limbs in sub-parallel mechanism
在R-Pa4s支链中,4-DOF是将Pa4s中被补偿而消失的自由度当作被动关节放置在平行四边形前端;2-DOF虚拟弹簧是为减去Pa4s中4-DOF的被动运动只保留存在刚度的自由度方向。由此,得到支链的一般性运动变形方程如下:
(12)
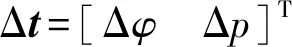
文献[29]中给出了支链的笛卡儿矩阵表达形式:
(13)
i=1,2
而分支链1、2中相应的柔度矩阵为
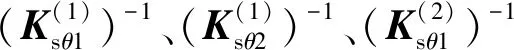

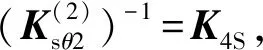
3.1.2子并联机构的刚度矩阵
这样,混合支链的柔性模型为子并联机构和串联支链部分的组合,如图8所示。
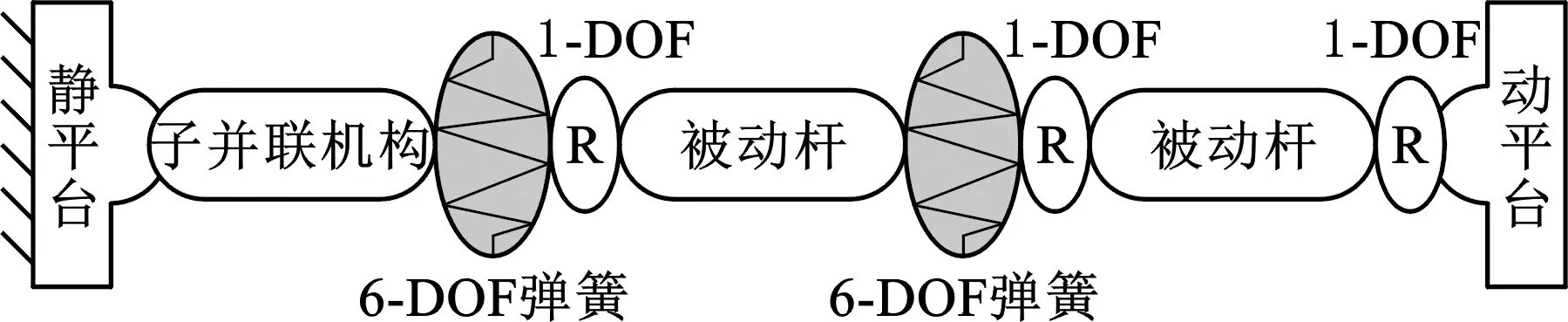
图8 混合支链的柔性模型Fig.8 Flexible model of the mixed limb
其中,子并联机构末端的6-DOF虚拟弹簧是将子并联机构看作整体,描述其在笛卡儿空间内的六自由度的弹性变形。
通过代入相应的截面系数和材料系数,得到混合支链1、 2中相应的柔度矩阵分别为
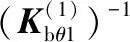
3.1.3机构的刚度矩阵
3.2 基于CAD模型的参数识别
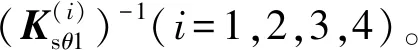
依次施加不同方向的单位力与力矩,得到局部坐标系中相应方向的变形,将变形作为主动臂柔度矩阵中的元素,如下式所示:
Ksθ=
(14)
用同样的方法,可分别得到该操作手中其他各杆件的柔度矩阵[23],为后续的刚度性能分析提供参数。
3.3 刚度性能指标的分析
笛卡儿刚度矩阵中存在量纲不一致的问题。为避免量纲不一致对所分析机构在不同位置时刚度特性的影响,文献[32]提出基于虚功原理的刚度指标,定义虚功刚度指标(单位:1/J)为
在相同单位外力/外力矩funit下,外力做功越小,产生的动平台位姿变化越小,因此,WV指标数值越大,该位置的刚度性能越好。
3.3.1机构的单方向承载性能
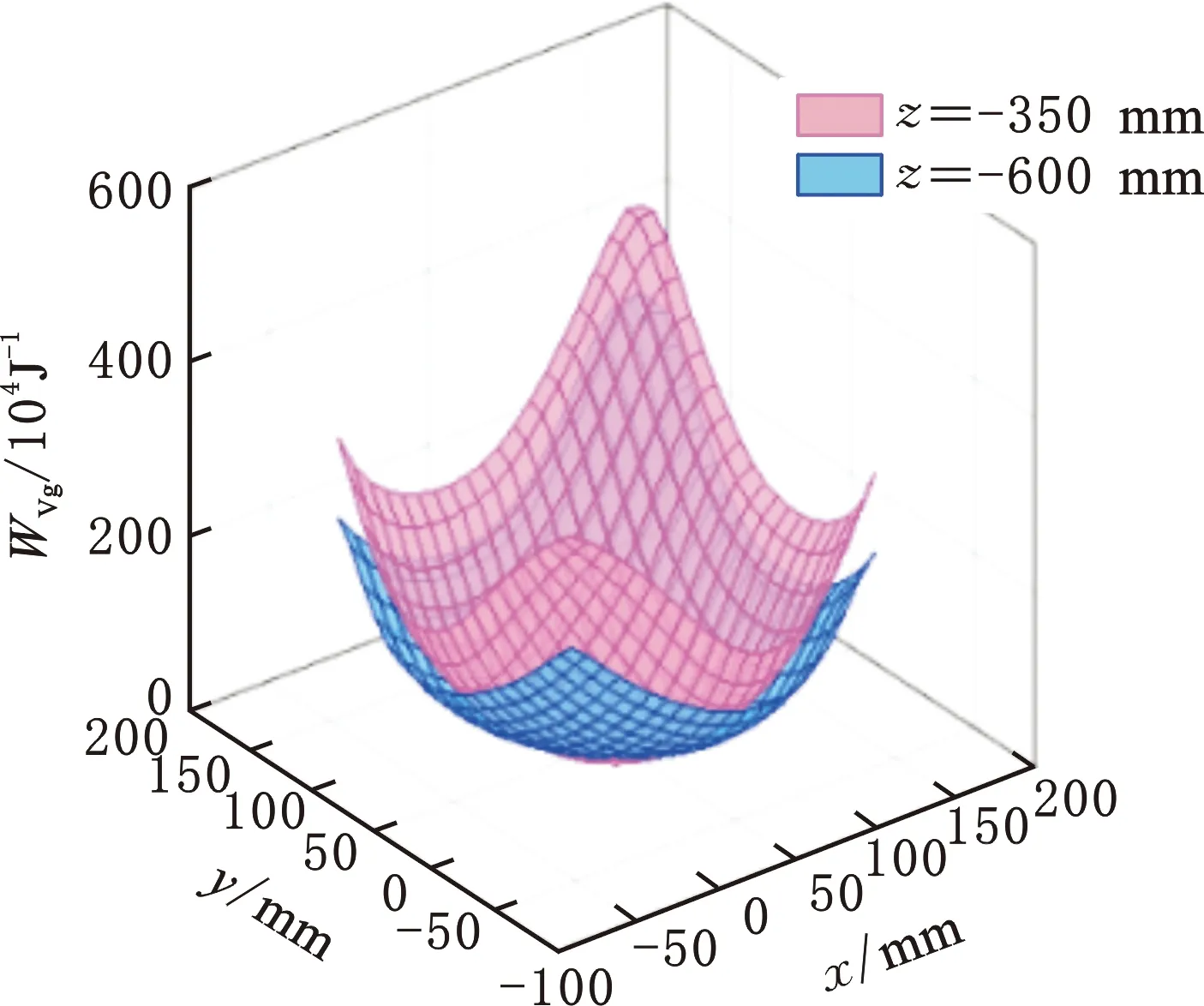
对该并联操作手而言,假设动平台在静坐标系中受到重力方向单位负载fg=(0,0,0,0,0,-1)T(N),运用WV刚度指标可计算得到该负载下的指标值WVg。例如在工作空间中,z=-350 mm和z=-600 mm的平面在定姿态α=45°下的刚度指标变化如图9a所示;同时,在z=-450 mm的平面上选定多个姿态的刚度指标变化,如图9b所示。
(a)不同平面(α=45°)

(b)不同姿态 (z=-450 mm)图9 WVg指标的变化图Fig.9 Variation about WVg index
由图9可知,该并联操作手在工作空间中的承载性能大体一致,即边界差、中间好;但随着动平台工作高度的减小或动平台转角的增大,承载性能会出现不同程度的减弱。
3.3.2机构的整体刚度性能
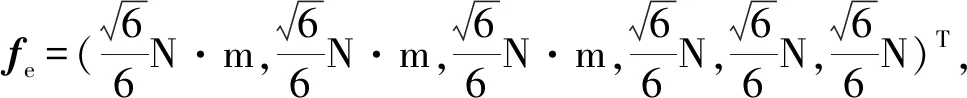
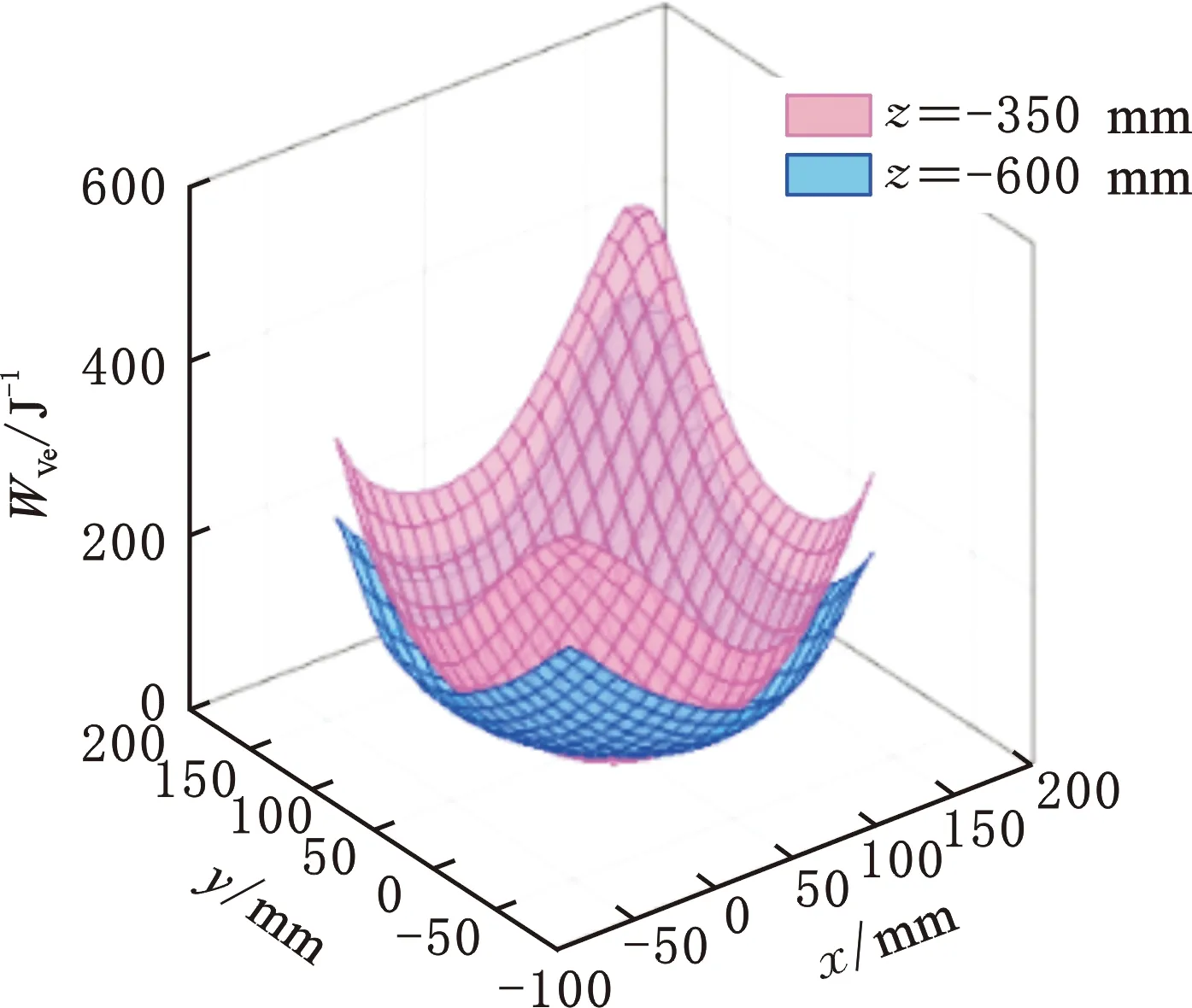
(a)不同平面(α=45°)

(b)不同姿态(z=-450 mm)图10 WVe指标的变化图Fig.10 Variation about WVe index
由图10可知,该机构的整体刚度性能的变化趋势与承载性能相反,在边界时刚度性能较好,中间时刚度性能差;而在不同姿态下,整体刚度性能变化趋势发生了改变,动平台转角越大,指标值呈波浪式变化的趋势越明显。
3.4 基于智能算法的刚度性能优化
3.4.1确定截面参数约束条件
由于复杂构件(如主动杆为多孔构件)的柔度矩阵很难通过具体公式进行计算,因此,优化设计时需将柔度矩阵中所有的元素作为设计变量,但过多的设计变量又会明显增加优化设计过程中的计算量和时间损耗,因此,可适当简化复杂构件的设计变量,在材料参数与尺度参数不变的情况下,通过复杂构件的柔度矩阵,近似估计出与其对应的规则截面的杆件,从而减少设计变量数目,提高优化思路的实用性。
通过式(14)和截面惯性矩的计算方法[33],对各复杂拓扑构件的截面参数进行近似估计,表5所示为各构件等效后的截面参数和弹性参数,而构件弹性模量为210 GPa,泊松比为0.3。
2.3节已对机构运动学性能(工作空间、运动/力传递)进行优化,并得到一组优化的结构参数。在杆件壁厚确定的情况下,限制杆件材料体积,以达到优化杆件截面参数、提高材料利用率,并降低制造成本的目的,因此,确定杆件壁厚均为2 mm,则杆件的刚度设计参数简化为单一的外径Q。
表6中各杆件的外径分别记为Qi(i=1,2,3,4),则设计变量为Q=[Q1Q2Q3Q4]。为避免优化后杆件直径过小不易加工,设计变量的上下限参考第2.4.1节,也以原始设计变量的50%作为优化时设计变量的取值范围,见表6。

表6 截面参数的设计变量及其变化范围
3.4.2确定目标函数

3.3节已基于虚功刚度性能指标分别建立了关于机构单方向承载性能、整体刚度性能的指标,由此,定义操作手的这两个刚度性能指标为其优化设计目标,即
将并联机构的承载刚度性能和整体刚度性能综合考虑,分别赋予50%的指标权重,经过归一化处理,得到刚度性能优化的目标函数为
(15)
3.4.3优化过程分析和结果比较
取2.4.3节中表5的尺度优化参数,对三种智能算法进行初始化设置(表2),再分别对机构的刚度性能进行优化,其优化过程如图11所示。
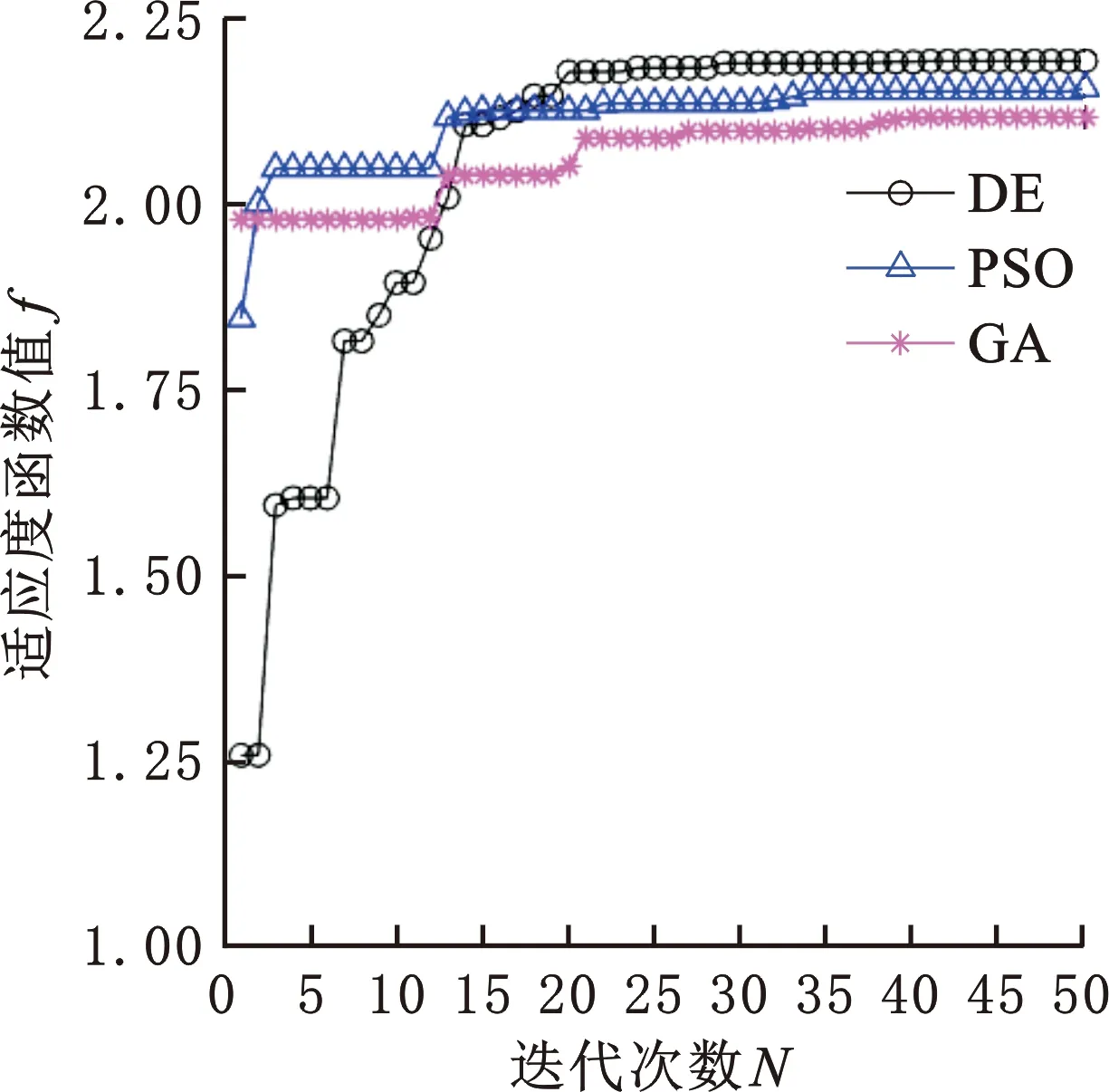
图11 刚度参数优化过程及其计算曲线Fig.11 Optimization process and calculation curve of stiffness parameters
将三种优化算法得到的截面参数最优解、最优目标函数值、计算时间等进行比较,如表7所示。
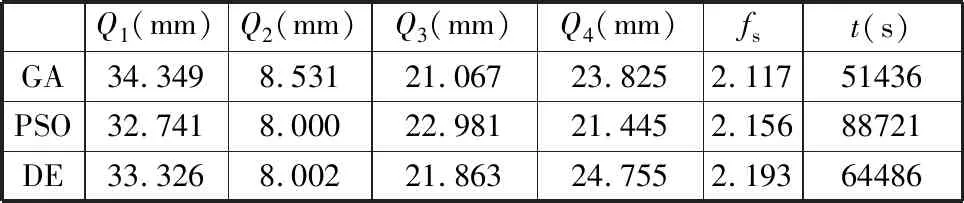
表7 优化前后的截面参数和刚度性能指标fs
由图11可看出:①有限次迭代后,GA算法未达到最优的目标函数值就已收敛;②就优化效果(即fs值)而言,DE算法取得了最好的效果,GA和PSO算法均未求得最优解;③由表7可知,从优化结果(即截面参数值)分析,DE与PSO和GA算法得到的截面优化参数区别不大,但DE算法的效果最优,说明PSO算法陷入了局部最优,也说明该机构刚度性能优化时存在相近峰值。
将DE方法优化后的截面参数进行圆整,对优化前后的两个刚度性能指标(承载性能、整体刚度)进行比较,如表8所示。
由表8可知,优化后,选定的两种刚度性能指标都有明显提高,承载刚度提高了150.788%,整体刚度提高了88.548%。
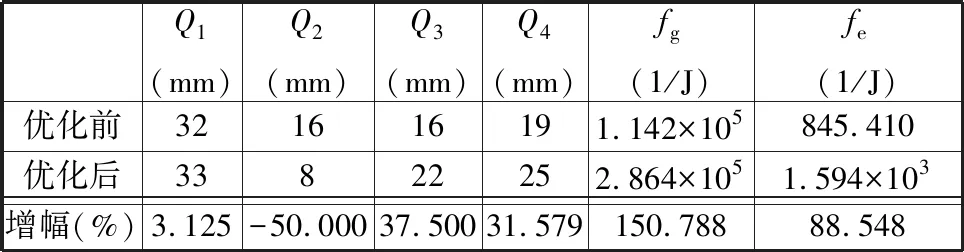
表8 刚度性能优化后的截面参数及性能
根据优化前后截面参数变化的对比,得到该机构截面尺度设计的一些准则:①Pa4s结构中长边杆的刚度对机构的刚度性能影响较小,可大幅减小Q2的尺寸;②子并联机构和混合支链中的被动杆的直径Q3、Q4都应增大,以提高机构的整体刚度。
4 动力学质量参数的优化
4.1 基于动力学普遍方程的动力学建模
目前,刚体动力学建模主要有牛顿-欧拉(Newton-Euler)方程[34-36]、动力学普遍方程(又称虚功原理)[37-38]、拉格朗日(Lagrange)方程[39-40]、凯恩(Kane)方程[41-42]等四种方法。本节运用动力学普遍方程,通过对该并联操作手的每个构件进行受力分析,并利用虚功原理得到机构的动力学方程,进而求解动平台受力与输入力矩的关系。
4.1.1速度模型
由式(9)、式(10)即可得到两个子并联机构中关于Ci(i=1,2,3,4)和θi(i=1,2,3,4)的位置约束方程:
((C2-A1)-lbb1)·e1=0
((C3-A4)-lbb4)·e4=0
将上述方程分别对t求导,得
(16)
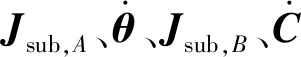
(17)
(18)
(P-lppi+leK-Ci)·ei=0
(19)
i=2,3
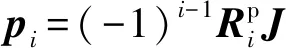
(20)
(21)
i=2,3
Wi=P-lppi+leK-Ci
将式(20)和式(21)化为矩阵形式,得到雅可比矩阵:
(22)
式中四个分量的表达式请扫描本文OSID二维码查看。
将式(17)代入式(22)得
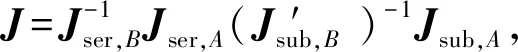
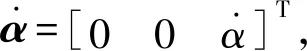
(23)
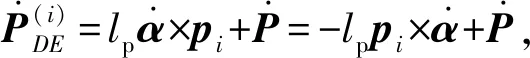

(24)
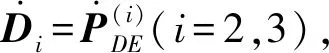
(25)
i=2,3
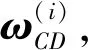

(26)
因子动平台仅有平移运动,则质心处的速度为
(27)
因主动杆AiBi(i=1,2,3,4)的角速度可表示为
(28)
i=1,2,3,4
则主动杆末端的速度可表示为
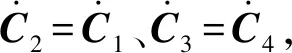
i=1,2,3,4
由此,可得到被动杆的角速度
主动杆一端固定在静平台上,因此其质心速度应为
4.1.2加速度模型
对式(23)关于时间t求一阶偏导,得
(29)
对式(24)求一阶偏导,得杆件DiEi(i=2,3)质心的加速度为
(30)
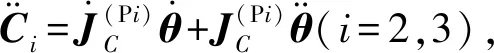
i=2,3
对式(26)求一阶偏导,得杆件CiDi(i=2,3)的角加速度
(31)

(32)
进一步,可解得杆件BiCi、主动杆件AiBi(i=1,2,3,4)质心的加速度分别为
(33)
4.1.3动力学普遍方程建模
设均匀动平台的质心在其中心,利用达朗贝尔原理,动平台的受力情况可表示为
(34)
式中,fex、Mex分别为作用在动平台中心的外力和外力矩;mP为动平台质量;OIP为动平台在静坐标系中的转动惯量。
杆件DiEi(i=2,3)在静坐标系中仅有移动没有转动,则
(35)
i=2,3
式中,mDE为杆件DiEi(i=2,3)的质量。
因杆件CiDi始终做平面转动,则
(36)
i=2,3
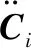
因子动平台始终只有移动没有转动,则子动平台的受力为
(37)
i=2,3
式中,mC为子动平台的质量。
杆件BiCi的受力为
(38)
i=1,2,3,4
式中,mBC为杆件BiCi的质量;BIBC为杆件BiCi在局部坐标系中的转动惯量,因杆件BiCi在局部坐标中存在二维转动,则其转动惯量需进行坐标系的转换[23]。
杆件AB的受力为
(39)
i=1,2,3,4

根据虚位移原理[43],由各杆件的受力方程得到机构的动力学普遍方程为
(40)
式中,δP、δα为各构件对应的虚位移和虚转角。
根据式(23)~式(33),将式(40)改写为关于驱动副虚转角δθ的形式,得到
δθ=0
(41)
因式(41)是针对任意虚转角δθ的,则可得到
(JP)TfP+(Jα)TMP+
(42)
将式(23)、式(33)代入式(42)中,化简得到动力学方程的一般形式为
(43)
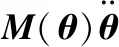
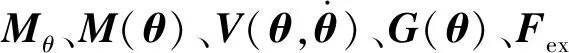
4.2 动力学性能指标的分析
4.2.1动力学灵巧度
KM=‖M(θ)‖2·‖M(θ)-1‖2
(44)
式中,KM为惯性矩阵的条件数,KM越小,机构的加速度性能越好。
因惯性矩阵仅与机构位姿有关,在原始尺度参数和质量参数下,可计算该机构在不同位姿下的动力学灵巧度变化。例,图12a所示为z=-350 mm和z=-600 mm的平面在定姿态α=45°下的动力学灵巧度变化;图12b所示为在z=-450 mm的平面上,多个姿态(α=45°,90°,180°)下的动力学灵巧度变化。
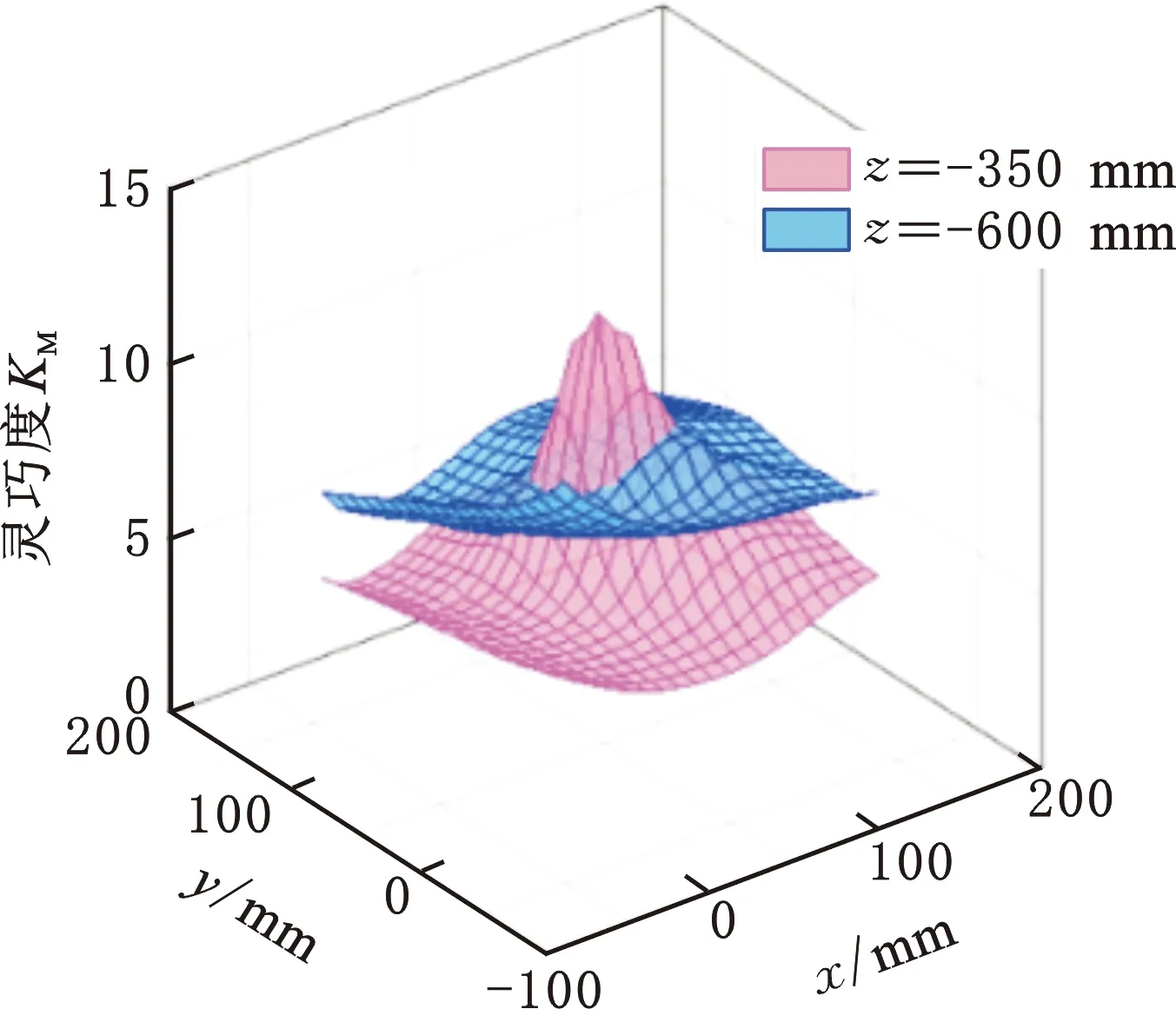
(a)不同平面(α=45°)
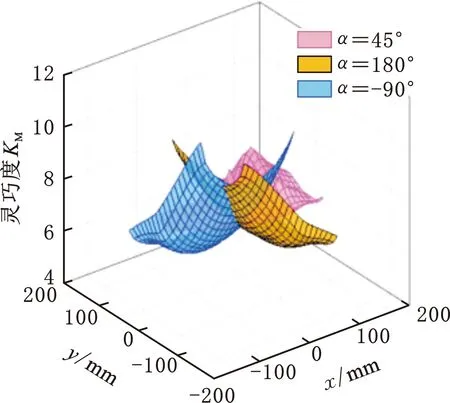
(b)不同姿态(z=-450 mm)图12 动力学灵巧度的变化Fig.12 Variation about dynamics dexterity
由图12可知:该机构在不同高度上,灵巧度的变化趋势不同,即工作高度越高,运动学灵巧度变化趋势越明显,其中,在工作平面中心处,加速度性能较差,越往边缘移动,性能越好;而在较低的工作平面上变化比较平稳。当动平台在不同位姿时,灵巧度呈现完全不同的变化趋势,在α=45°时,加速度性能中间差,四周好;而在两对称姿态(α=-90°和α=180°)下,加速度性能从运动边界的一侧,逐渐减弱到另一侧。
4.2.2能量传递效率
为克服惯性矩阵量纲不一致问题,有学者提出基于能量传递效率的动力学指标[44],即将其定义为动平台的动能(EP)与机构系统整体动能(T)的比值,用ζP表示能量传递效率:

(45)

4.3 基于智能算法的动力学性能优化
4.3.1确定质量参数的约束条件
在已优化尺度参数和截面参数,即给定构件体积的情况下,对构件的质量参数进行优化设计。为方便优化计算,将机构中各构件的转动惯量视为常量,仅考虑各构件质量对机构动力学性能的影响,而动平台处的质量受外负载影响而定,因此,确定设计变量为m={mDE,mCD,mC,mBC,mAB}。
同样,以原始质量的50%作为变化量,确定各构件的质量变化范围,如表9所示。

表9 质量参数的设计变量及其变化范围
通过计算各构件的原始质量,得到
mmin=mDE,min+mCD,min+mC,min+
mBC,min+mAB,min=1.645 kg
则优化过程中设计变量应满足总体约束:
mDE+mCD+mC+mBC+mAB>mmin
4.3.2确定目标函数
机构动力学优化设计的目标函数是动力学灵巧度及能量传递效率同时达到最大化,即定义
fP→max
动力学灵巧度反映的是机构在一定输入力矩下的加速度能力,而能量传递效率反映的是动平台在机构总体动能中的占比,物理意义比较明确,因此,分别赋予60%和40%的指标权重。经计算在原始质量参数下,这两个动力学指标分别为fM=0.075,fP=0.697,由此,得到动力学性能优化的整体目标函数为
(46)
4.3.3优化问题分析和结果比较
同样,先对三种智能算法进行初始化设置,再用这三种方法分别对机构动力学性能进行优化计算,其优化过程如图13所示。

图13 动力学质量参数优化过程及其计算曲线Fig.13 Optimization process and calculation curve of dynamic mass parameters
将三种算法得到的质量参数的最优解、目标函数和计算时间进行比较,如表10所示。
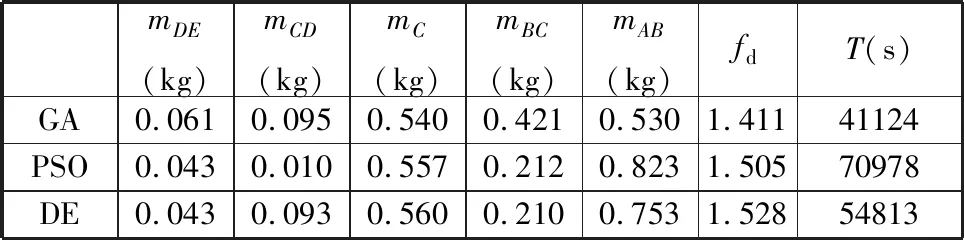
表10 优化前后的质量参数和性能指标fd
由图13可知,有限次迭代后,①GA算法远未达到最优的目标函数值就已接近收敛;②就优化效果(即fd值)而言,DE算法取得了最好的效果,且用时最短,GA和PSO算法均未求得最优解。③从优化结果(即质量参数值)分析,DE和PSO算法得到的质量参数的区别较小,但DE算法的结果更优,说明PSO算法陷入了局部最优,也说明该机构动力学性能优化时存在相近峰值。
将DE方法优化前后得到的动力学性能指标进行比较,如表11所示。
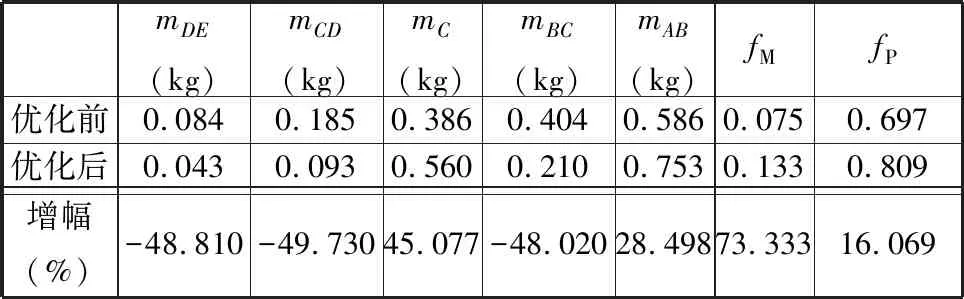
表11 动力学性能优化前后的质量参数及其指标的对比
由表11可知,优化后,选定的两种动力学性能指标都有明显提高,动力学灵巧度提高了73.333%,能量传递效率提高了16.069%。
根据优化前后质量参数变化的对比,得到该机构质量参数设计的一些准则:①Pa4s结构中长边杆的质量对机构的动力学性能影响较小,可大幅减小mBC的大小;②应尽量减小从动杆的质量(如mDE、mCD),从而改善机构的动力学性能。
上述优化计算时计算机硬件配置信息如下:处理器为Intel(R) Core(TM) i5-8300H CPU,四核八线程;基本频率为2.30 GHz;内存为16 G;软件为MATLAB 2016a。
本文提出的基于运动学、刚度和动力学性能的有序递进三级优化策略和方法及其在2-(RPa3R)3R型SCARA并联操作手机构的综合参数优化(尺度、截面及质量参数)上的应用过程可用图14的流程图表示。这种有序递进三级优化策略和方法,如果再考虑机构的拓扑特征[45],更有利于参数求解和提高计算效率。
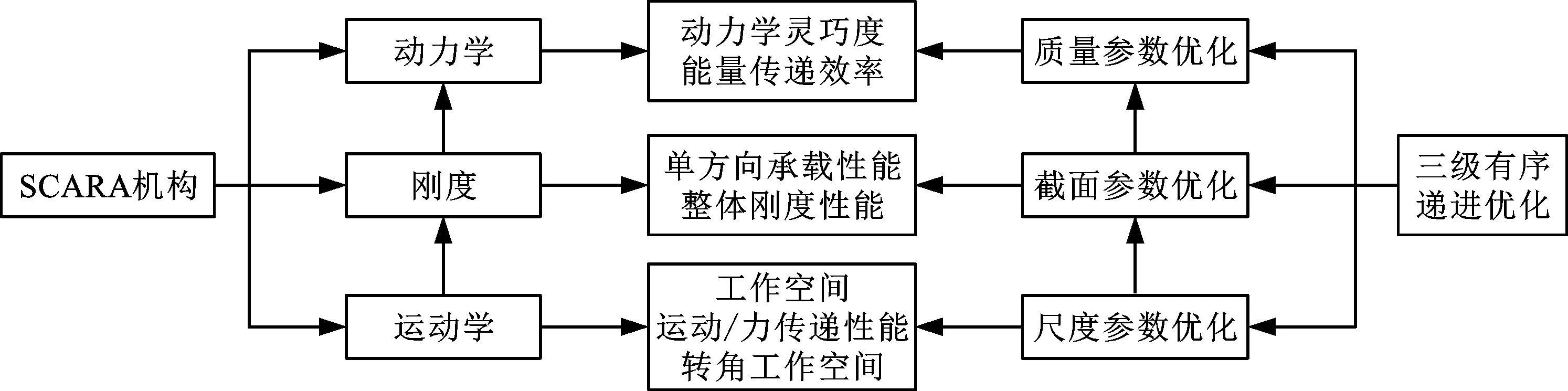
图14 并联机构的有序递进三级优化策略和方法流程图Fig 14 Flow chart of the three-level orderly proceeding optimization strategy and method of parallel mechanism
5 结论
提出一种基于运动学、刚度和动力学性能的并联机构有序递进三级优化策略和方法,以20(RPa3R)3R并联操作手为例,对其运动学性能、刚度性能和动力学性能分别进行了分析,并运用GA、PSO、DE三种智能算法分别进行了优化设计,得到以下结论:
(1)有序递进三级优化设计策略和方法具有优化参数全面(涉及尺度参数、截面参数、质量参数)、优化方法综合运算能力强、各自优化结果不抵触且优化有序等优势;而该并联操作手的耦合度为零并具有部分运动解耦性,使得其运动学、刚度和动力学分析求解方便。
(2)通过对比GA、PSO、DE三种智能算法在运动学、刚度和动力学中的优化计算效果,DE算法在牺牲了一定计算速度的基础上得到了最好的优化结果,其收敛的准确性最高,因此,在并联操作手的优化设计中,DE智能算法中具有较明显的优势。
(3)目标函数的不同权重并不总能指导智能算法进行计算,若单一目标性能增幅过大,会影响权重系数发挥作用;而过多的目标函数,又很难进行清晰的表达,因此,在目标性能优化时,各性能优化的有效性上还需要进一步研究和探索。
