航空涡轮轴发动机复杂转子的动力学建模方法
2022-07-25王龙凯王艾伦尹伊君
王龙凯 王艾伦 尹伊君 金 淼 衡 星
1.中南大学轻合金研究院,长沙,4100832.中南大学高性能复杂制造国家重点实验室,长沙,410083
0 引言
航空涡轮轴发动机是现代直升飞机的动力来源[1]。高效低振转子系统[2-3]的设计是航空发动机研究的重点内容,而构建合理且计算高效的转子动力学模型是开展动力学设计和振动评估的关键。
目前,国内外学者在航空发动机转子的建模和振动特性等方面开展了大量的研究,采用的转子建模方法主要有传递矩阵法、有限元法、集总参数法和模态综合法[4-5]。基于有限元离散法,陈果[5]结合梁单元与刚性盘方程建立了双转子动力学耦合模型;雷冰龙等[6]、章健等[7]采用ANSYS构建了涡轮轴发动机转子的三维实体有限元模型;SINHA[8]、YU等[9]采用有限元法对简化的涡扇发动机双转子进行了突加不平衡响应的研究。殷杰等[10]采用方程分析法得到了畸变相似模型的固有频率;王艾伦等[11]采用ANSYS研究了燃气轮机转子的疲劳-蠕变损伤。WANG等[12]基于有限元法研究了涡轮增压转子不平衡振动特性。杨喜关等[13]采用固定界面模态综合法推导了双转子运动方程。MENG等[14]采用传递矩阵法预测了重型燃机临界转速。黑棣等[15]、何谦等[16]采用集总参数法分别研究了组合转子横向和轴向的振动。GREENHILL等[17]针对Timoshenko梁单元方程仅限于圆柱形单元这一问题,推导了线性锥形梁单元的运动方程,并通过ANSYS验证了方程的有效性。CHEN[18]基于Guyan法和有限元法计算了等截面梁在不同边界条件下的固有频率,所得计算结果与解析解一致。上述文献中,集总参数法和传递矩阵法在实际应用中虽简化了求解过程,但难以获得真实的振动特性;ANSYS三维实体有限元法虽能考虑复杂结构的局部细节,但因总自由度过大而难以求解瞬态响应;等截面梁单元的有限元法和模态综合法由于模型复杂度高和求解瞬态响应耗时长,而在实际应用中有较多限制。因此,亟需建立一种计算量小且能真实反映复杂转子结构特征的通用动力学模型。
笔者基于有限元和Guyan缩减,采用子结构法对复杂结构进行等效和自由度缩减,构建了复杂转子系统的动力学模型。为验证建模方法的正确性,设计了相应的转子试验台,结合理论分析与试验对模型的有效性进行了验证,并得到了涡轮轴发动机燃气发生器转子的振动特性。
1 涡轮轴发动机结构特征
如图1所示,一种典型的高功重比涡轮轴发动机[6-7,19-20]主要由燃气发生器转子(下文简称“燃发转子”)和动力涡轮(自由涡轮)转子组成,其功率由动力涡轮向前输出。与涡扇双转子发动机相比,涡轮轴发动机两转子之间没有中介轴承连接,因此,可以单独构建燃发转子或动力涡轮转子的动力学模型来分析振动特性。

1.动力涡轮转子 2.燃发转子 3.一级轴流压气机 4.二级轴流压气机 5.三级轴流压气机 6.一级离心压气机 7.一级燃气涡轮 8.二级燃气涡轮 9.一级动力涡轮 10.二级动力涡轮 11.6号支承 12.5号支承 13.2号支承 14.1号支承 15.4号支承 16. 3号支承图1 涡轮轴发动机结构示意图Fig.1 Schematic diagram of turboshaft engine
动力涡轮转子主要由两级动力涡轮和动力传动轴组成,采用2-2-0(两支承-两支承-叶轮盘)的支承方式,属于典型的悬臂柔性转子。燃发转子采用1-0-1的支承方式、3级轴流串联1级离心压气机+2级燃气涡轮(3A1C+2T)的布局方式、长螺栓-螺母的装配方式。1号和2号支承采用鼠笼式弹性支承。与动力涡轮转子相比,燃发转子结构布局更加复杂、工作转速更高、建模求解更加困难。因此,本文以3A1C+2T结构布局的燃发转子为例,研究复杂转子的动力学建模方法,并对模型进行振动特性分析。
2 复杂结构建模及系统自由度缩减
中空圆柱形Timoshenko梁单元(图2a)的单元运动方程参考文献[5,9]。中空线性锥形梁单元[17]的轴向截面几何形状如图2b所示。图2中,s为梁单元的轴向位置坐标,l为梁单元长度,ξ为量纲一位置坐标,ξ=s/l;梁单元末端的内外半径分别为r和R,下标0、1分别表示单元左端(s=0)和右端(s=l);梁单元密度为ρ。定义单元左右端部的内径比Δi=r1/r0、外径比Δo=R1/R0,推导出轴向位置ξ处的内外半径分别为
rξ=r0[1+(Δi-1)ξ]
(1)
Rξ=R0[1+(Δo-1)ξ]
(2)
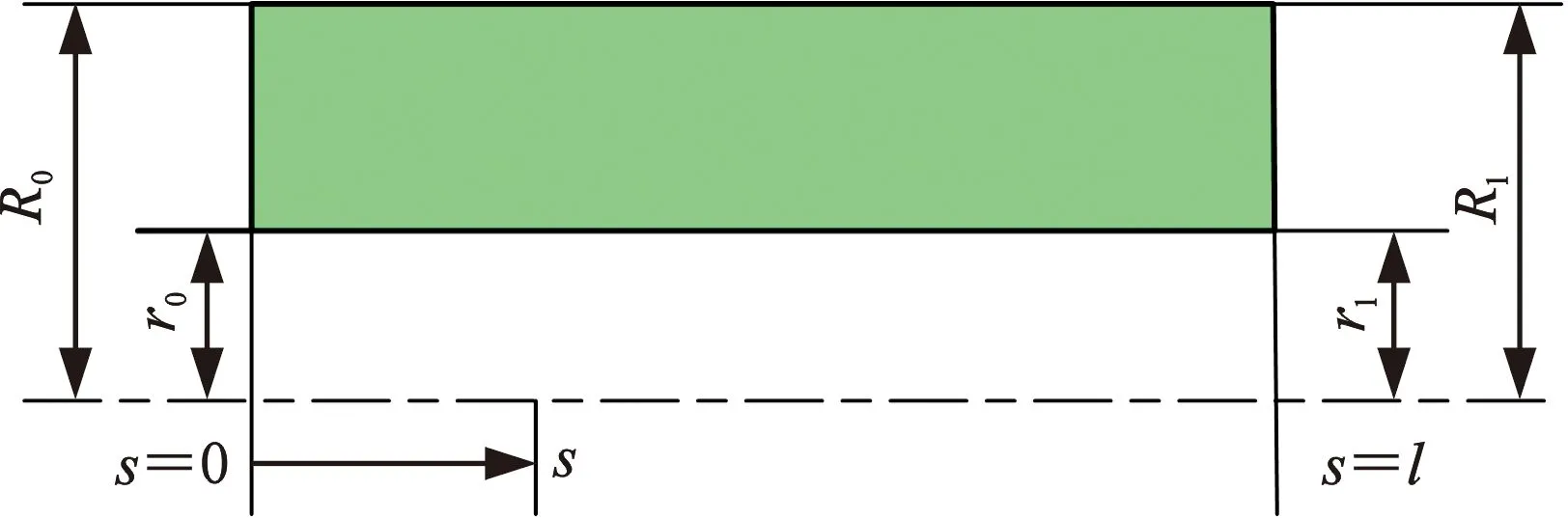
(a)圆柱形
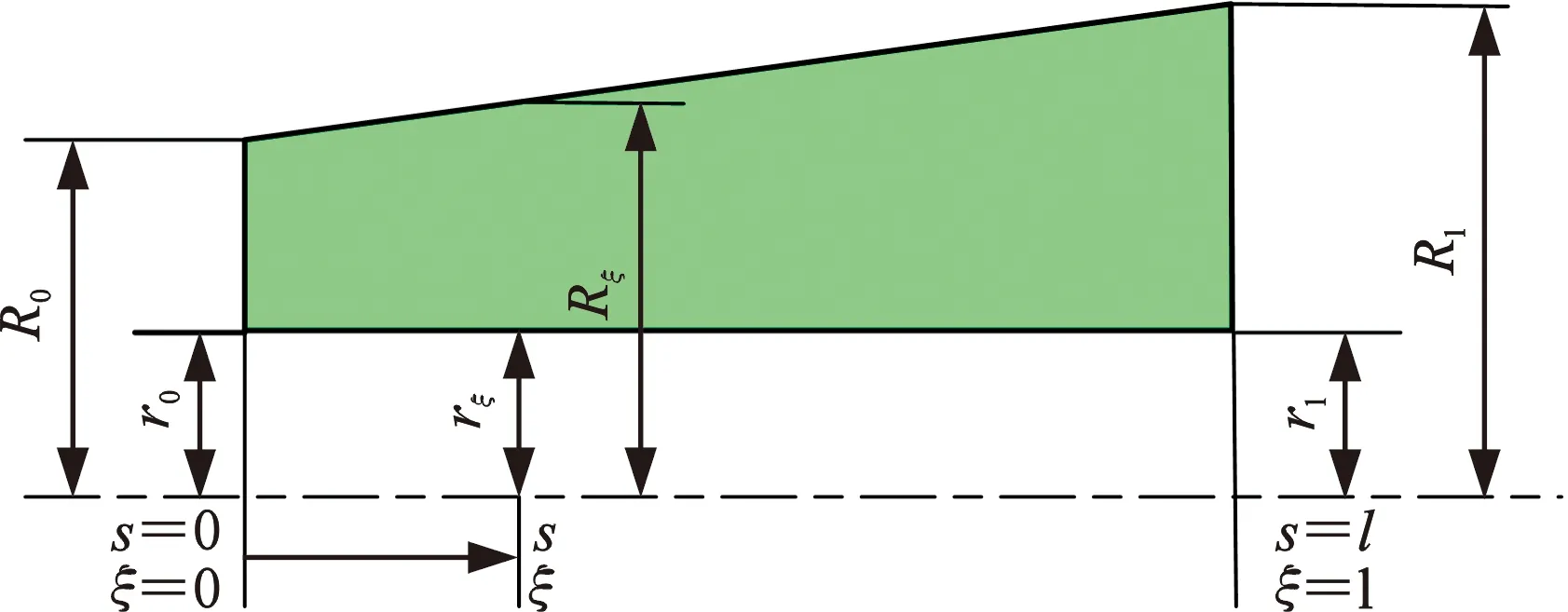
(b)线性圆锥形图2 两种梁单元Fig.2 Two types of beam elements
利用式(1)、式(2)可推导出坐标ξ处横截面的面积A和截面惯性矩I:
(3)
(4)
忽略锥形单元的轴向运动,设(xξ,yξ)、(βxξ,βyξ)和(θxξ,θyξ)分别为轴向坐标ξ处X向和Y向的位移、剪切变形和截面转角。单元端点的位移qe=(x0,y0,θx0,θy0,x1,y1,θx1,θy1,βx0,βy0,βx1,βy1)T,下标0表示单元左端点,下标1表示单元右端点。根据形函数理论和能量理论,采用拉格朗日方程可推导出12自由度锥形单元的运动控制方程[17]:
(5)
(6)
d2,1=d5,2=d6,5=-d6,1=2.4+1.2δ1+24δ2/35 +
3δ3/7+2δ4/7
d3,1=d4,2=d5,3=d6,4=-l(0.2+0.2δ1+δ2/7+
δ3/10+δ4/14)
d7,1=d8,2=-d7,5=-d8,6=
l(-0.2+2δ2/35+δ3/14+δ4/14)
d10,1=d12,1=-d9,2=-d11,2=-d10,5=
-d12,5=d9,6=d11,6=
-l(1.2+0.6δ1+12δ2/35+3δ3/14+δ4/7)
d4,3=l2(4/15+δ1/15+4δ2/105+11δ3/420+
2δ4/105)
d8,3=-d74=-l2(1/15+δ1/30+δ2/35+
11δ3/420+δ4/42)
d9,3=d11,3=d10,4=d12,4=
-l2(0.1+0.1δ1+δ2/14+0.05δ3+δ4/28)
d8,7=l2(4/15+0.2δ1+6δ2/35+13δ3/84+δ4/7)
d9,7=d11,7=d10,8=d12,8=
l2(-0.1+δ2/35+δ3/28+δ4/28)
d10,9=d12,9=-d11,10=d12,11=
l2(0.6+0.3δ1+6δ2/35+3δ3/28+δ4/14)
(7)
kB1,1=-kB5,1=-kB6,2=kB2,2=kB5,5=kB6,6=
12+6δ1+4.8δ2+4.2δ3+132δ4/35
kB4,1=-kB3,2=-kB5,4=kB6,3=
l(6+2δ1+1.4δ2+1.2δ3+38δ4/35)
kB8,1=-kB7,2=-kB8,5=kB7,6=
l(6+4δ1+3.4δ2+3δ3+94δ4/35)
kB9,1=kB11,1=kB10,2=kB12,2=-kB9,5=-kB11,5=
-kB10,6=-kB12,6=-l(6+3δ1+
2.4δ2+2.1δ3+66δ4/35)
kB3,3=kB4,4=l2(4+δ1+8δ2/15+0.4δ3+12δ4/35)
kB7,3=kB8,4=l2(2+δ1+13δ2/15+0.8δ3+26δ4/35)
kB10,3=kB12,3=-kB9,4=-kB11,4=
l2(3+δ1+0.7δ2+0.6δ3+19δ4/35)
kB7,7=kB8,8=l2(4+3δ1+38δ2/15+2.2δ3+68δ4/35)
kB10,7=kB12,7=-kB9,8=-kB11,8=
l2(3+2δ1+1.7δ2+1.5δ3+47δ4/35)
kB11,9=kB10,10=kB12,10=kB11,11=kB12,12=
l2(3+1.5δ1+1.2δ2+1.05δ3+33δ4/35)
(8)
kS9,9=kS10,10=1/3 +α1/12+α2/30
kS11,9=kS12,10=kS9,11=kS10,12=1/6+α1/12+α2/20
kS11,11=kS12,12=1/3 +α1/4+α2/5
(9)
mR1,1=-mR5,1=-mR6,2=mR2,2=mR5,5=
mR6,6=1.2+0.6δ1+12δ2/35+3δ3/14+δ4/7
mR4,1=-mR3,2=mR6,3=-mR5,4=
l(0.1+0.1δ1+δ2/14+0.05δ3+δ4/28)
mR8,1=-mR7,2=-mR8,5=mR7,6=
l(0.1-δ2/35-δ3/28-δ4/28)
mR9,1=mR11,1=mR10,2=mR12,2=-mR9,5=
-mR11,5=-mR10,6=-mR12,6=-l(0.6+
0.3δ1+6δ2/35+3δ3/28+δ4/14)
mR3,3=mR4,4=l2(119/887+δ1/30+2δ2/105+
11δ3/840+δ4/105)
mR7,3=mR8,4=-l2(1/30+δ1/60+δ2/70+
11δ3/840+δ4/84)
mR10,3=mR12,3=mR9,4=-mR11,4=
l2(0.05+0.05δ1+δ2/28+δ3/40+δ4/56)
mR7,7=mR8,8=l2(2/15+0.1δ1+3δ2/35+
13δ3/168+δ4/14)
mR10,7=mR12,7=-mR9,8=-mR11,8=
l2(0.05-δ2/70-δ3/56-δ4/56)
mR9,9=mR11,9=mR10,10=mR12,10=mR11,11=
mR12,12=l2(0.3+0.15δ1+3δ2/35+
3δ3/56+δ4/28)
(10)
mT1,1=mT2,2=13/35+3α1/35+19α1/630
mT4,1=-mT9,1=-mT3,2=-mT10,2=
l(11/210+α1/60+4α2/593)
mT5,1=mT6,2=9/70+9α1/140+23α2/630
mT11,1=mT7,2=mT12,2=-mT8,1=
l(13/420+α1/70+3α2/398)
mT3,3=mT10,3=mT4,4=-mT9,4=mT9,9=
mT10,10=l2(1/105+α1/280+α2/630)
mT6,3=-mT5,4=mT9,5=mT10,6=
-l(13/420+α1/60+5α2/504)
mT7,3=mT12,3=mT8,4=-mT11,4=mT10,7=
-mT9,8=mT11,9=mT12,10=
-l2(1/140+α1/280+α2/504)
mT5,5=mT6,6=13/35+2α1/7+29α2/126
mT8,5=-mT11,5=-mT7,6=-mT12,6=
-l(11/210+α1/28+13α2/504)
mT7,7=mT12,7=mT8,8=-mT11,8=mT11,11=
mT12,12=l2(1/105+α1/168+α2/252)
为便于计算,将式(6)~式(10)都降维为8×8的单元矩阵。降维过程可表示为
(11)

高速旋转机械的结构非常复杂,涡轮轴发动机燃发转子各级压气机叶轮盘和涡轮盘的合理等效是构建有效动力学模型的关键。图3给出了复杂结构的建模流程,首先分段线性拟合复杂型面;然后采用圆柱形梁单元与锥形梁单元相结合的方式对复杂结构进行单元划分,其中,12×12的锥形单元矩阵(式(6)~式(10))通过式(11)约简为等效的一系列8×8的矩阵;最后根据节点划分情况和主单元内子单元分布情况进行子单元自由度缩减,得到主单元的陀螺矩阵、刚度矩阵和惯性矩阵。

图3 复杂结构建模Fig.3 Complex structure modeling
图4所示的主单元n含有3个圆柱子单元和1个锥形子单元,qL、qs1、qs2、qs3、qR均为4自由度的位移向量。该模型的5个结点均有4个自由度(共计20个自由度),因此基于Guyan矩阵缩减法[18]进行自由度缩减。图4所示的子单元自由度缩减过程如下。
将各子单元的运动方程进行集成,可得到结点n至结点n+1的运动方程:
(12)
qn1=[qLqs1qs2qs3qR]=[qLqsqR]
式中,MTn1、MRn1、Dn1和Kn1分别为平移质量矩阵、旋转惯性矩阵、陀螺矩阵和刚度矩阵。
采用与式(11)相同的转换方式得到各主单元8×8质量/刚度/陀螺矩阵。由矩阵转换可知,在主单元层次对子单元自由度进行缩减可有效减少整个系统的自由度,从而减小计算量。
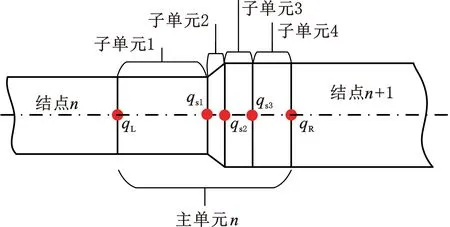
图4 主单元及子单元Fig.4 The master-elements and sub-elements
3 复杂转子系统的动力学模型
针对图1所示涡轮轴发动机燃发转子系统,根据转子结构特点和转子建模方法,构建图5所示的转子-轴承系统动力学模型,图中,Kb1、Kb2分别为1号和2号支承处的刚度,Cb1、Cb2分别为1号和2号支承处的阻尼系数(见表1),Kxx、Kyy分别为支承X向和Y向的刚度,Cxx、Cyy分别为支承X向和Y向的阻尼系数(按结构阻尼比4%计算)。采用M-S表示主单元M的第S个子单元。构建的复杂转子动力学模型由17个主单元(每个子单元含若干个子单元)、18个主结点、2个支承和6个模拟叶片特性的刚性盘构成,共72个自由度。结点2和17为支承位置,结点4、7、8、11、14和15为模化叶片刚性盘[5]与转子连接位置。
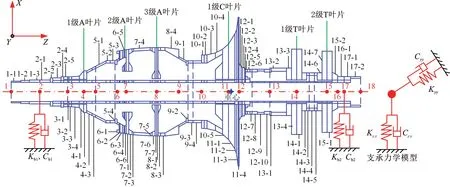
图5 涡轮轴发动机燃发转子有限元动力学模型Fig.5 FE dynamic model of gas generator rotor for the turboshaft engine

表1 轴承动力特性系数
鉴于滚动轴承和鼠笼弹支组件的刚度(支承刚度)可视为2个串联的弹簧刚度,则支承刚度可由公式1/K=1/K1+1/K2计算得到,其中,滚动轴承刚度K1、鼠笼弹支刚度K2的计算方法参考航发设计手册[4],滚动轴承型号为71910CE。
在得到各个主单元的运动方程后,在单元结点位置对转子主单元运动方程进行集成,推导出整个系统的运动方程:
(13)
qr=(x1,y1,θx1,θy1,x2,y2,θx2,θy2,…,
x18,y18,θx18,θy18)T
式中,MT、Mr、Dr、Kr分别为转子系统全局质量、旋转惯性、陀螺和刚度的矩阵;Cr为结构阻尼矩阵,Cr=αKr+β(MT+Mr),α、β为Rayleigh阻尼参数[21-22];Fg、Fub分别为重力和不平衡力。
不平衡力的一般形式为
(14)
式中,Fux、Fuy分别为不平衡力Fu在X向和Y向的力分量;m为不平衡质量;e为偏心距;φu为相位角。
4 算例分析
为验证动力学建模方法的合理性和正确性,采用本文的复杂结构建模与自由度缩减方法分别构建含有17个主单元(内含75个子单元)、18个主结点的模型1(图5),以及75个单元、76个结点的模型2,分析对比两模型求解得到的动力学特性的一致性,其中,模型2未进行自由度缩减,模型1和模型2结构参数、支承参数和求解方法均一致。
4.1 振型及临界转速
假定转子系统是各向同性的,对齐次方程(式(13))进行特征值分析,得到模态振型(图6)和临界转速(表2)。由图6可知,该涡轮轴发动机燃发转子前四阶振型分别为平动振型、俯仰振型、1阶弯曲振型和2阶弯曲振型,其中,前两阶振型可视为刚体模态,后两阶振型为典型的弯曲模态。对比2个模型的前四阶振型及临界转速可知,2个模型的振型基本一致且临界转速误差小于1%,但在计算耗时方面,模型1比模型2节约37.95%。上述分析表明本文复杂转子建模方法的正确性和有效性。
4.2 稳态不平响应
在各叶轮盘处分别施加2×10-6kg·m[18]的不平衡量,根据式(14)计算各结点处的不平衡力,以及转速2000~80 000 r/min范围内的稳态不平衡响应。图7、表3所示的结果表明2个模型的峰值转速和峰值振幅基本一致,且共振峰值转速与4.1节计算结果基本一致。模型1计算耗时比模型2节约了74.41%。上述分析表明,本文模型在保证计算精度的前提下,能大量节约求解时间。
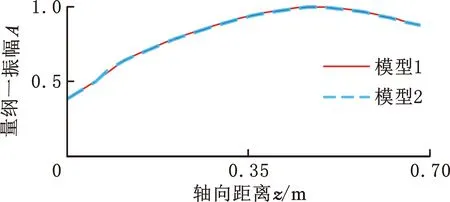
(a)一阶振型
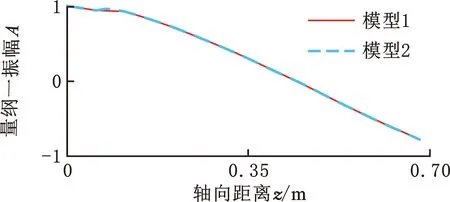
(b)二阶振型
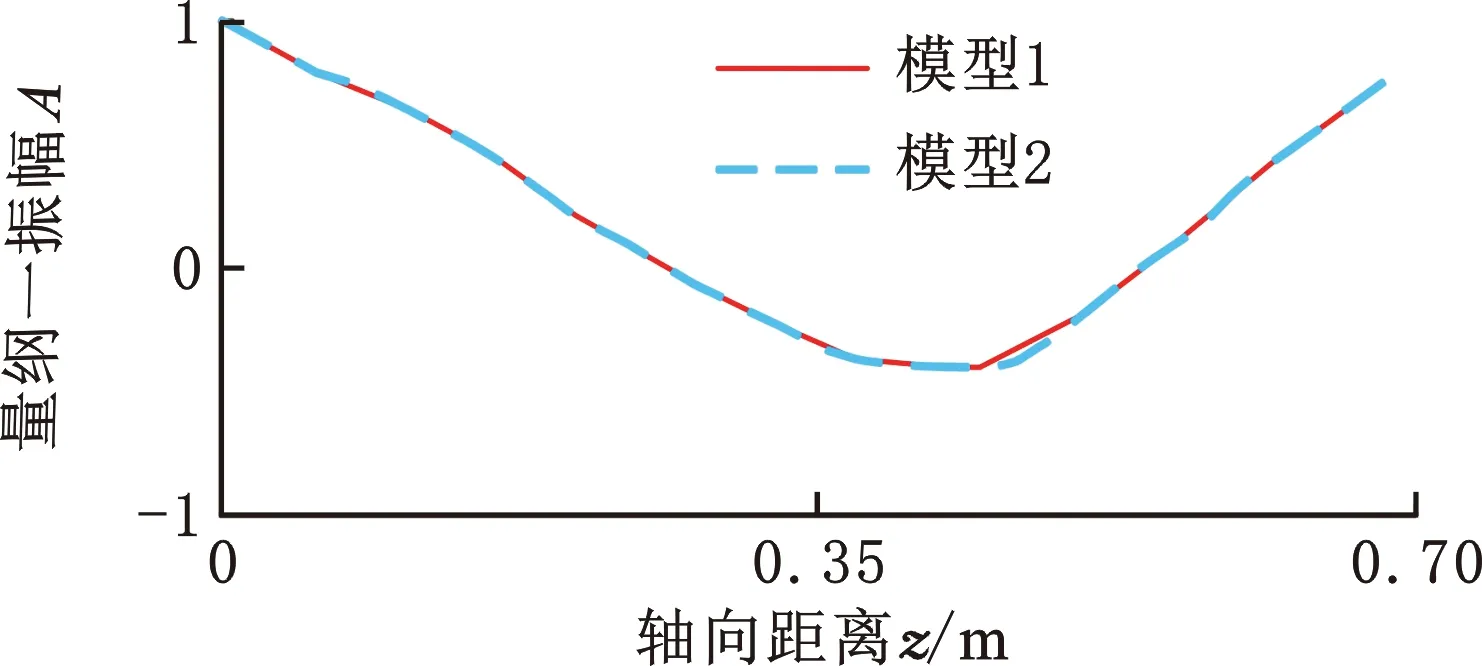
(c)三阶振型

(d)四阶振型图6 前四阶模态振型Fig.6 The first four mode shape
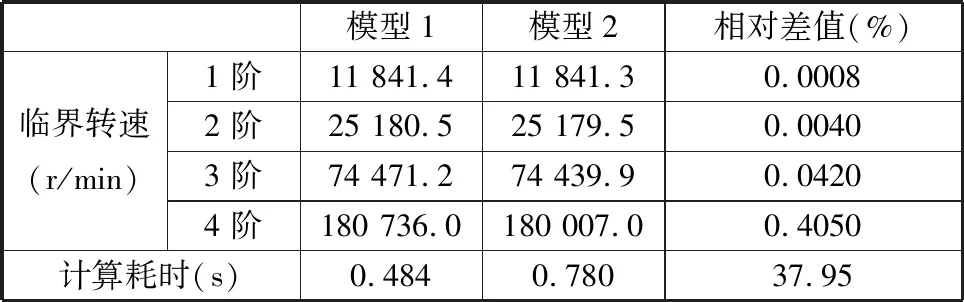
表2 前四阶临界转速及计算耗时
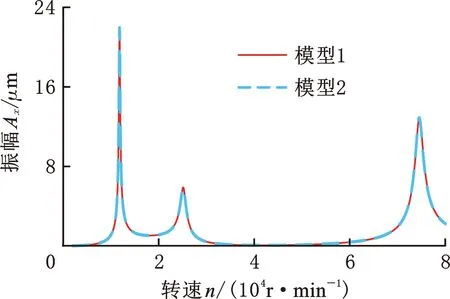
图7 幅频响应曲线Fig.7 Amplitude-frequency response curve

表3 模型结果及计算耗时
4.3 瞬态动力响应
在约束和边界条件与4.2节一致的前提下,对式(13)进行数值求解,得到转子系统的瞬时响应。图8所示为1号轴承在4个转速下的瞬态响应,0.49~0.5 s内的振动波形均为正弦波,由振动波形可知2个模型的数值计算结果基本一致。
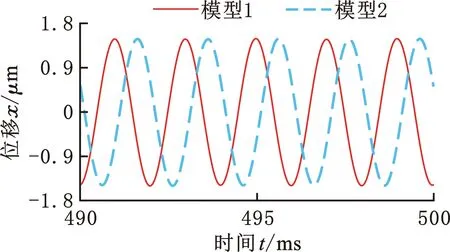
(a)3×104 r/min
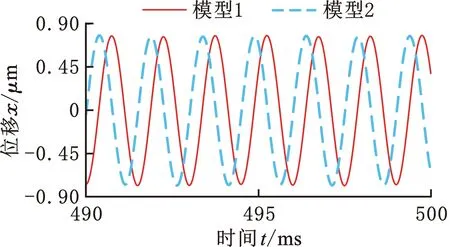
(b)4×104 r/min
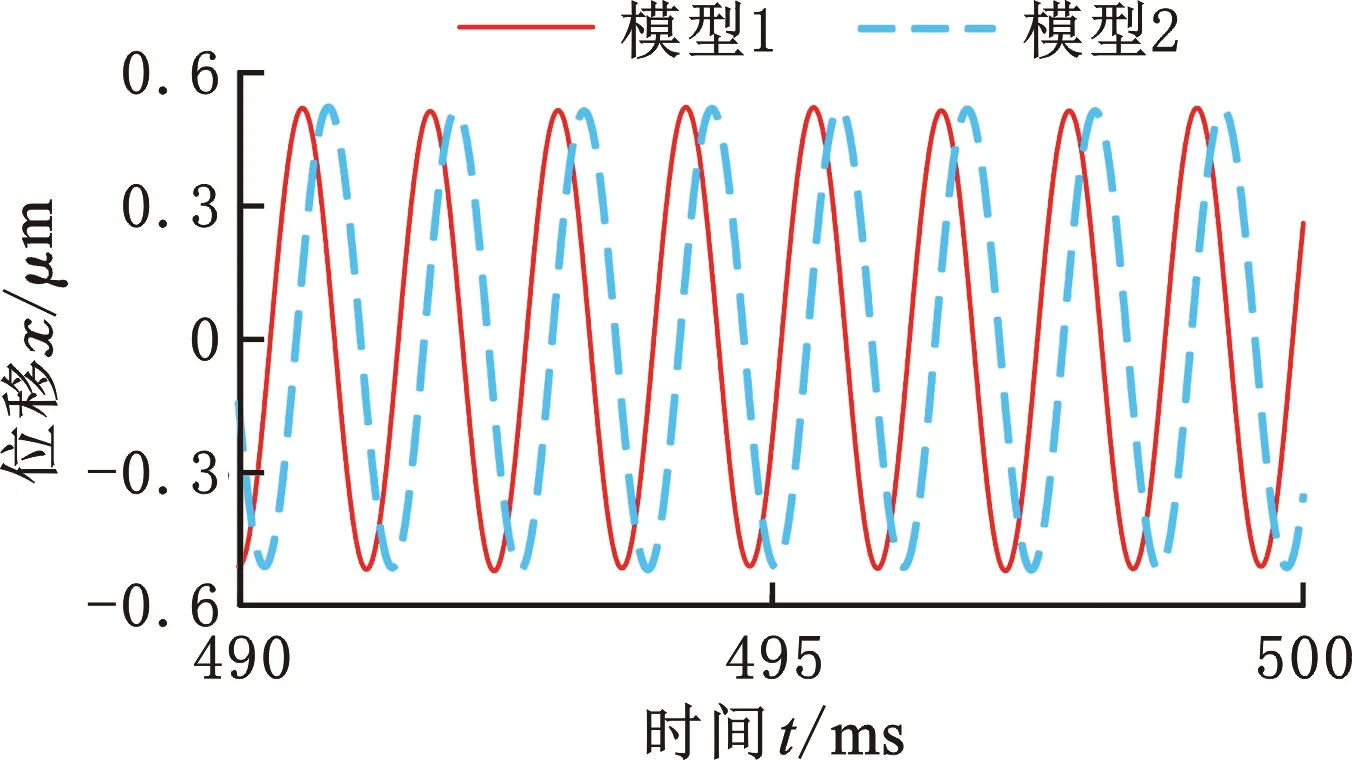
(c)5×104 r/min
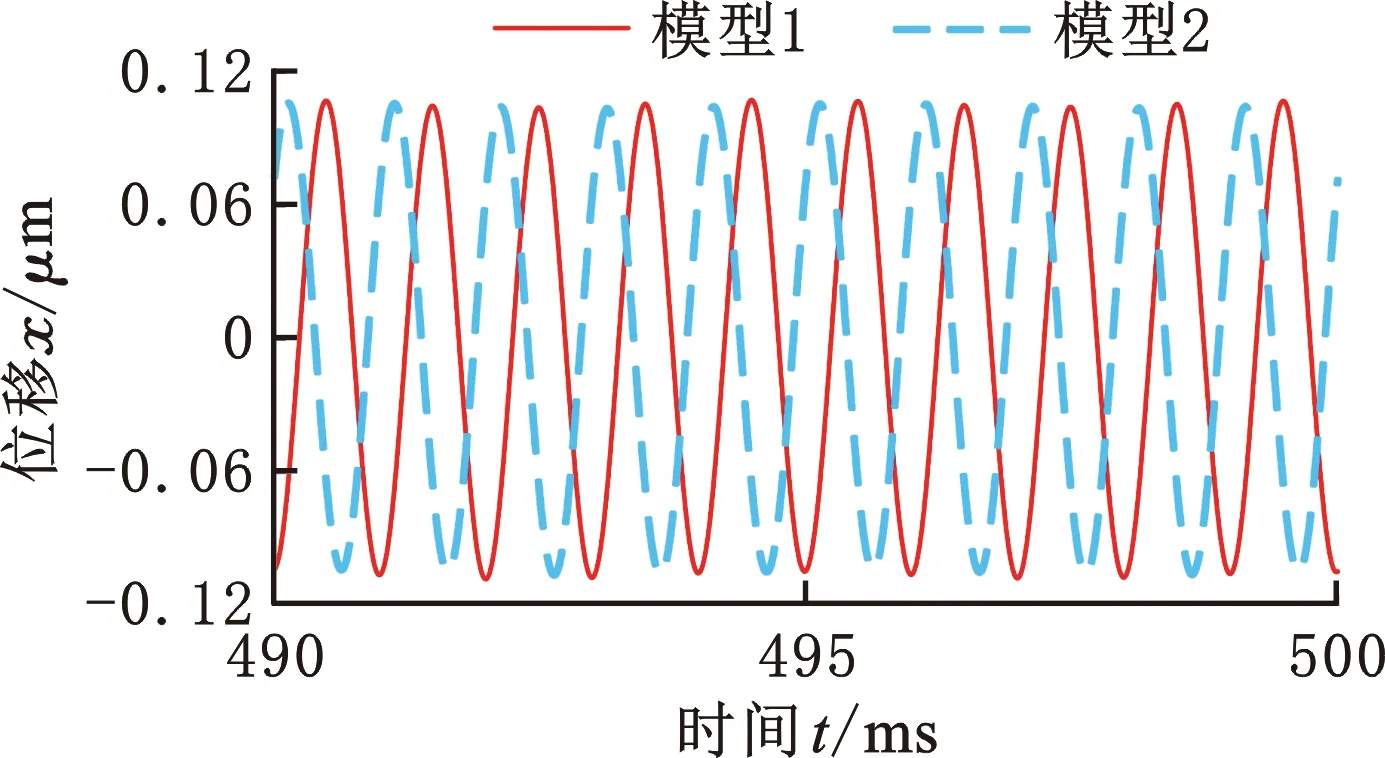
(d)6×104 r/min图8 1号轴承的时间瞬态响应Fig.8 Time transient response at No.1 bearing
0.48~0.5 s内,2个模型在不同转速下的振动响应均方根误差基本一致,如表4所示,最大相对误差1.01%证明了转子建模的正确性。如表5所示,模型1的求解时间约为模型2的1/30。上述分析表明本文模型能显著降低模型的复杂度、减少计算耗时,从瞬态响应角度验证了本文模型的有效性和优越性。
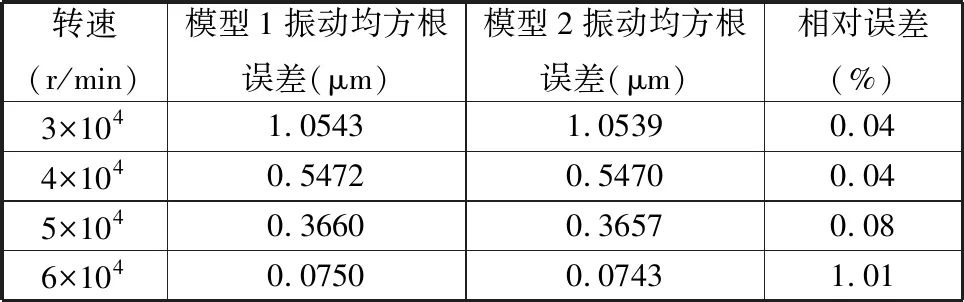
表4 不同转速下的模型振动均方根误差
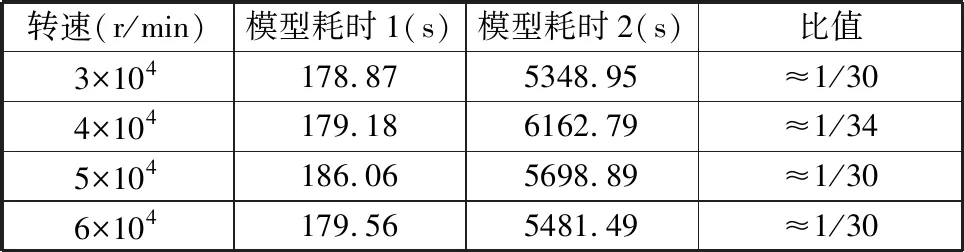
表5 不同转速下的模型计算耗时
5 试验研究
为进一步验证本文建模方法的有效性,针对航空涡轮轴发动机转子的结构特征,基于部分结构相似准则及研究目标,设计了图9所示的转子结构,并搭建了转子振动试验台。采用本文建模方法对试验转子进行建模处理,建立由11个结点、10个单元组成的转子动力学模型,通过升速试验验证模型的有效性,从临界转速角度对比分析仿真和试验结果的一致性。
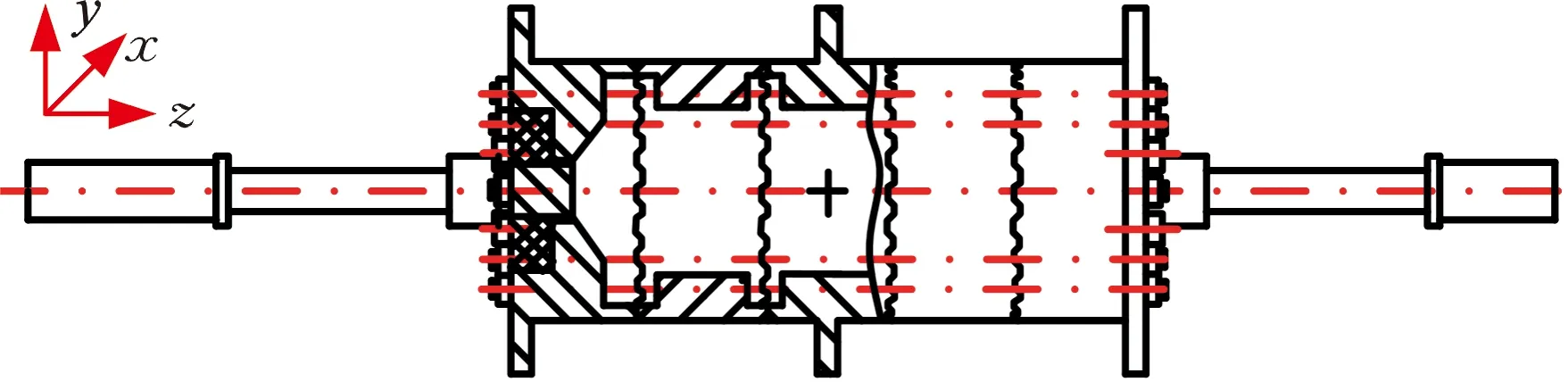
(a)转子结构示意图
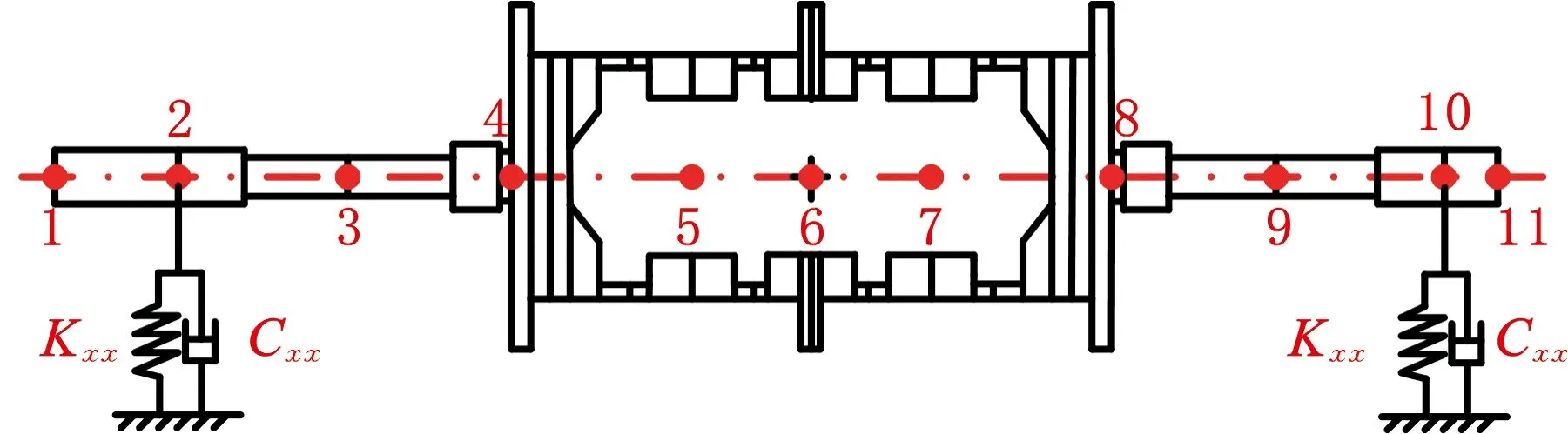
(b)动力学模型

(c)试验台实物图9 转子模型及试验台Fig.9 The rotor model and test rig
试验转子由变频器控制的三相交流电机驱动,两端轴承均为滚动轴承UCP205。采用压电式加速度传感器(灵敏度98.1 mV/g)采集轴承座的振动信号,采用光电传感器采集转速信号。为保证实测临界转速的可靠性,在同等条件下进行3次升速共振测试,对采集的信号进行阶次分析并取平均值,从而得到试验转子的幅频响应曲线。由图10可知,依据API 611,A0对应的转速为试验转子的临界转速。
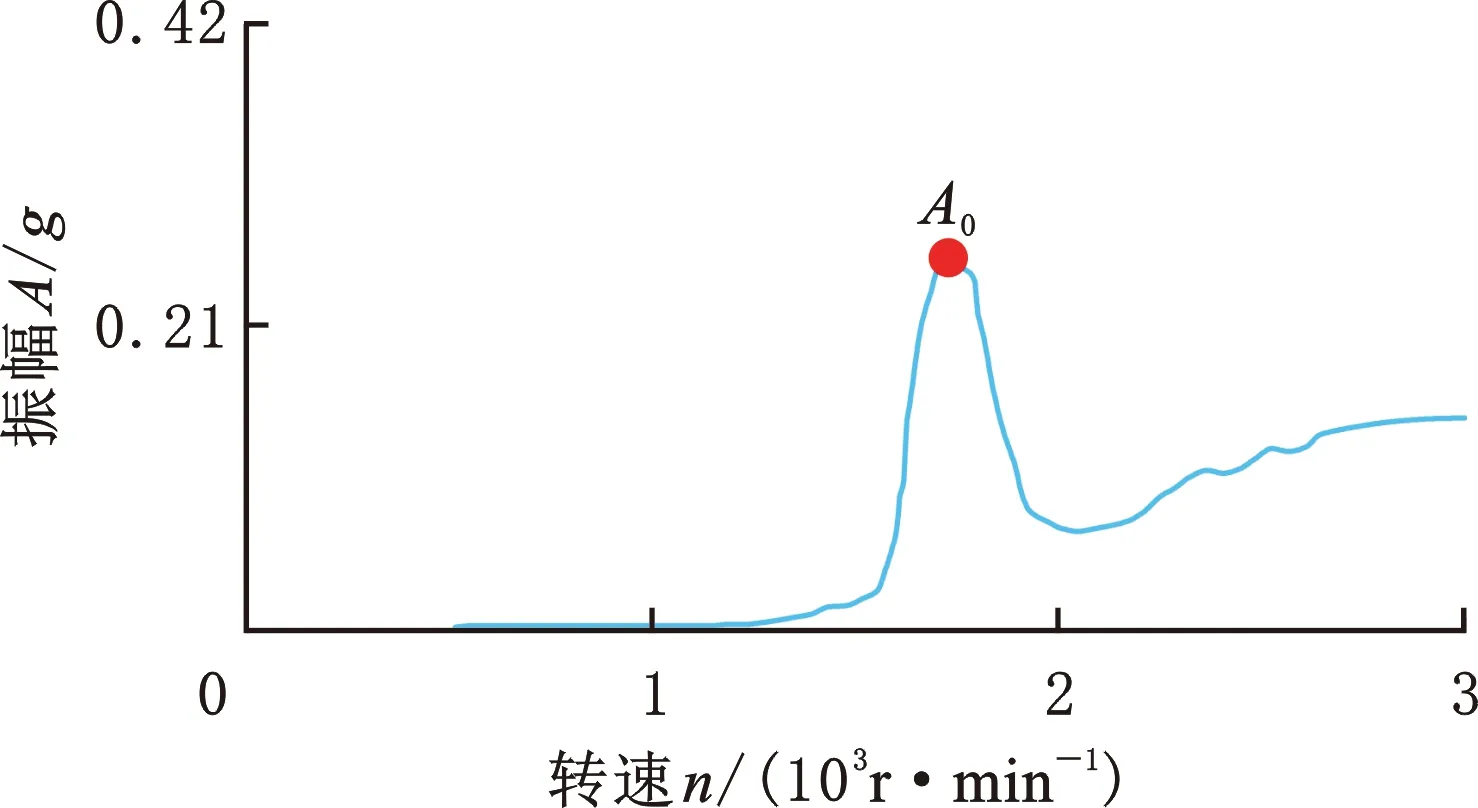
图10 试验转子升速工况幅频响应曲线Fig.10 Amplitude-frequency response curve of the test rotor under speed-up condition
试验转子的实测临界转速1725 r/min与本文模型的计算值1662 r/min的误差为3.65%,误差在工程允许误差范围之内,这表明本文构建的涡轮轴发动机燃气发生器等复杂转子模型可以很好地反映转子系统的动力学特性。
6 结论
(1)基于有限元法和分段线性拟合思想,采用主子单元对复杂转子结构进行建模,开展子结构自由度缩减及集成,推导出复杂转子系统全局运动方程。建立的数学模型显著降低了动力学模型的复杂度,并能详细表征转子的结构特点和力学特性。
(2)仿真分析验证了本文建模方法的有效性。对比分析临界转速、振型、幅频特性和瞬态动力响应发现,在保证求解精度的前提下,本文模型在预测转子幅频响应和瞬态动力学响应时具有计算耗时短的优势。
(3)针对航空涡轮轴发动机转子的结构特征,为验证基于部分结构的相似准则及模型准确性,设计了含锥形结构的多盘复杂转子结构并搭建了振动试验台,仿真分析和实测的结果较吻合,验证了本文方法的可行性。
