基于节点增强的功能点阵设计方法
2022-07-25徐赣君
徐赣君 戴 宁
南京航空航天大学机电学院,南京,210016
0 引言
增材制造能针对设计对象的特点为其提供专属设计方案,它不但能在宏观层面上实现结构的拓扑设计,还可以利用空间梯度上的变化提高结构的力学性能。目前,面向增材制造的设计方法主要有蒙皮点阵结构设计[1]、薄壁加筋结构设计[2]、一体化结构设计[3]、异形拓扑优化结构设计[4]。点阵是结构功能一体化的优良载体,对点阵结构的胞元进行参数化设计可实现轻质化、承载和减振等各项功能的有机融合[5],并已成功应用于生物医学[6]、汽车[7]和航空航天[8]等领域。早期的点阵结构研究主要通过数值模拟方法来预测其形状或性能的改变。王飞等[9]借助数值分析方法提出了点阵结构的细观力学模型,并将其用于预测不同相对密度的点阵结构在单向压缩过程中的变形、失稳和破坏。施月奇等[10]根据经典梁模型理论分析了点阵结构在复杂载荷作用的变形规律,研究表明,改变点阵结构的杆结构半径和倾角可以明显影响点阵结构的力学性能。
将功能点阵的理论研究应用到实际工程中的难点集中在探究材料最优分布和充分发挥力学性能。前者参照有限元分析结果,将均质点阵设计为梯度点阵,从而实现点阵结构力学性能的调控;后者通过改变点阵结构胞元的构型和几何尺寸,发挥点阵结构轻质高强度的优点。探究材料最优分布方面,赵芳垒等[11]对三点弯曲模型进行拓扑优化分析,并依据三点弯模型的相对密度对点阵结构进行重建,实验表明该方法能有效提高点阵的承载性能。DAYNESA等[12]参照主应力分析结果来改变均质点阵结构的胞元大小和构型,并将点阵结构沿应力等值线重新布局,从而生成承载性能更好的梯度点阵。DU PLESSIS等[13]依据均质点阵的有限元分析结果来增大高应力区域点阵的杆径,提高整体结构的承载性能。上述设计方法均参照有限元仿真结果对点阵进行优化设计,体现了有限元仿真分析对点阵建模的重要参考价值。
充分发挥力学性能方面,AREMU等[14]利用共形点阵设计方法提高了整体连通性,并验证共形点阵在复杂载荷下的力学性能比均质点阵的好。任利民等[15]通过边界强化模型构造的一种梯度点阵提高了蒙皮与点阵间的边界强度,保证了载荷的有效传递。KANG等[16]按照均质点阵结构拓扑优化后的相对密度设计了一种梯度点阵结构,实验表明该方法设计的梯度点阵结构的刚度和强度都比均质点阵明显提高。喻长江等[17]提出一种多级点阵结构的建模方法,并通过实验证明多级点阵具有更大的弹性模量和更优的断裂韧性。上述设计方法通过改变点阵胞元的构型,有效提高了点阵整体的承载能力。
本文提出了一种减振承载一体化的点阵设计方法,该方法对共形梁线构造体素化空间距离场并抽取等值面来生成共形点阵,依据梁模型的仿真分析结果对节点进行参数化调控。然后,以齿轮为载体对其辐板填充功能点阵。通过搭建的振动检测平台检测点阵型齿轮结构的振幅,并结合有限元仿真和承载实验检测点阵型齿轮结构的承载能力。
1 功能点阵结构设计
1.1 技术路线
功能点阵设计流程如图1所示。首先,对点阵梁线构造体素化空间距离场并抽取等值面,实现点阵结构建模。然后,根据给定功能设计要求对点阵结构的梁模型进行仿真,并参照仿真分析结果对节点进行参数化调控。
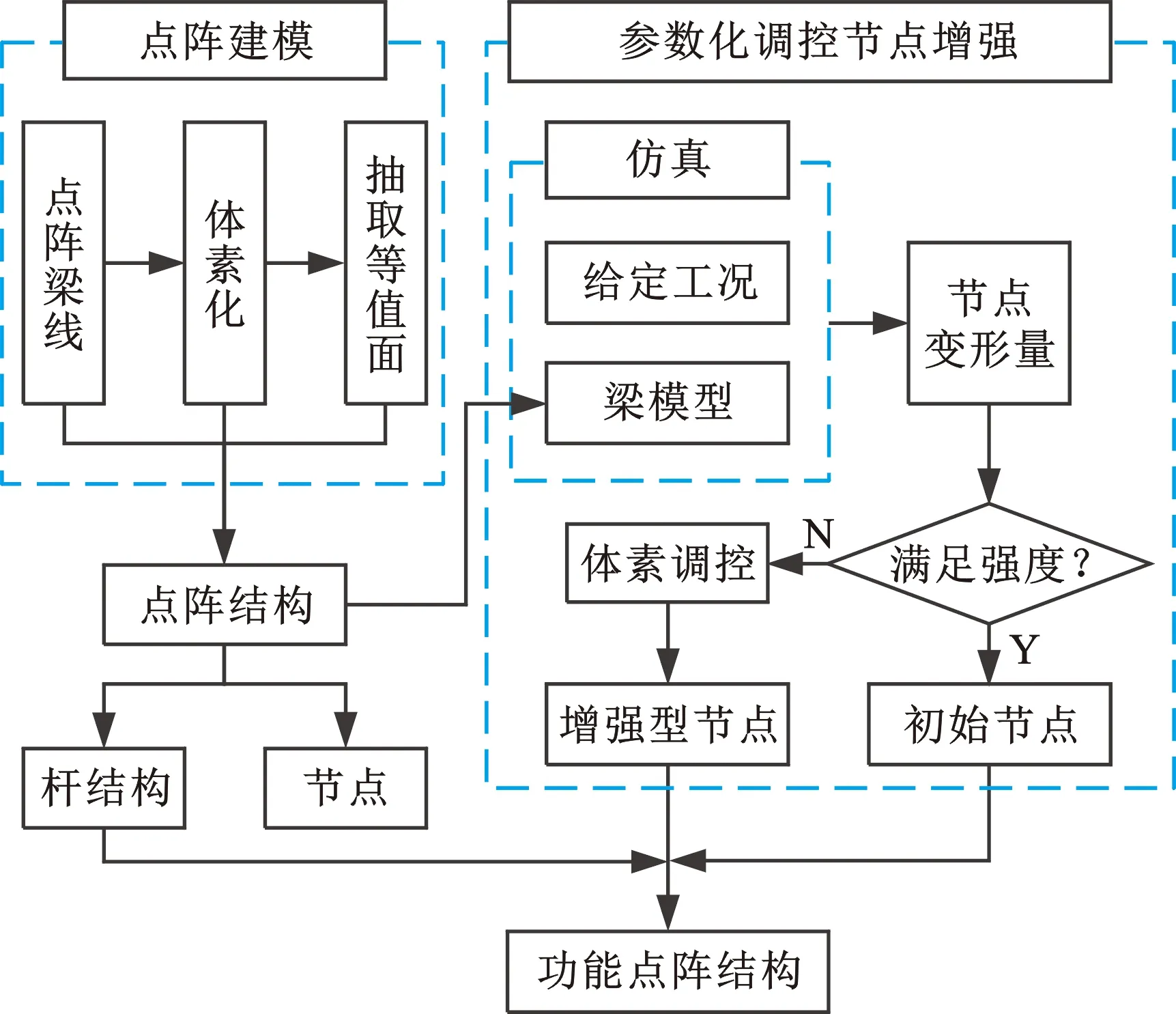
图1 功能点阵设计流程Fig.1 Functional lattice design workflow
1.2 点阵梁线
如图2a所示,在环形包围盒中创建点阵结构需要对点阵结构的梁线进行裁剪和连接,然而该方法会破坏其完整性,进而削弱边缘强度。因此本文采用适应环形面的共形梁线进行后续点阵设计,如图2b所示。
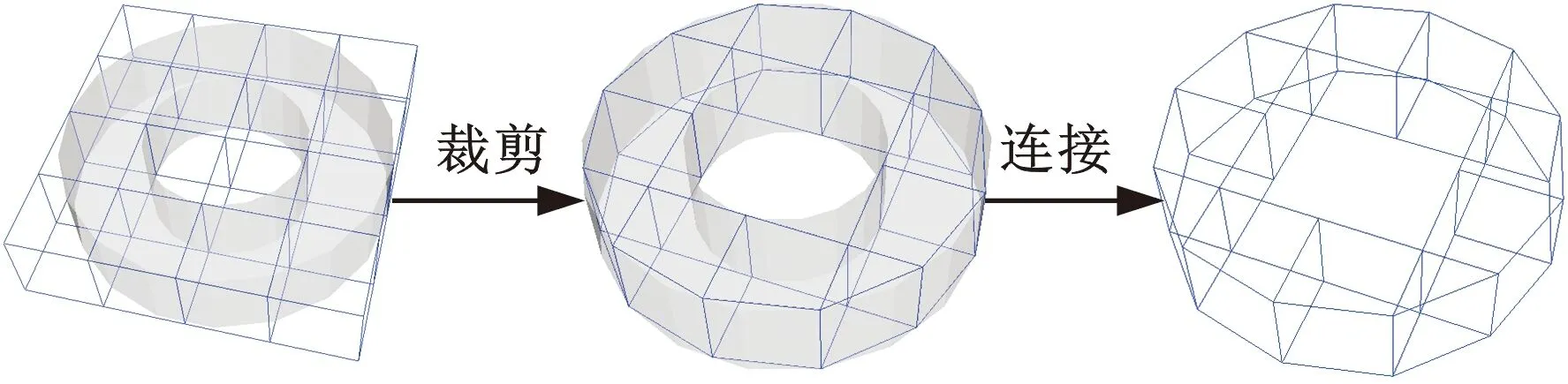
(a)非共形梁线
(b)共形梁线图2 环形包围盒内的点阵结构梁线Fig.2 Lattice structure beams for ring box
1.3 体素化空间距离场函数模型
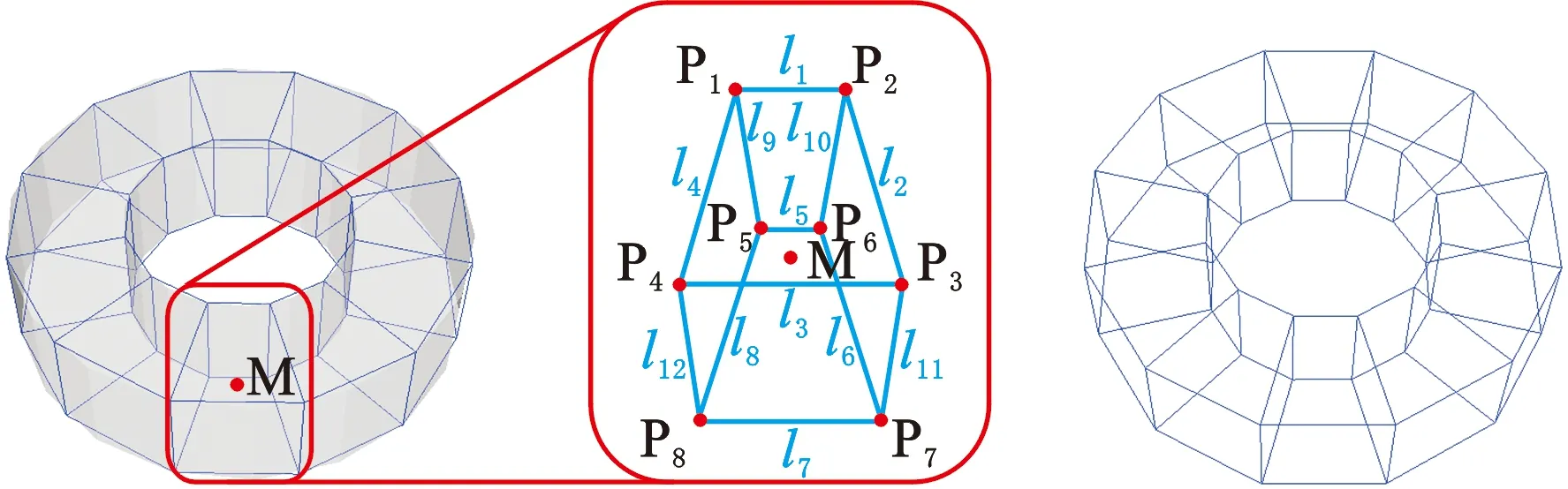
构造点阵实体结构的方式有两种:方法1,对点阵结构梁线赋半径相同的圆形截面来生成点阵结构,见图3a;方法2,先对点阵结构梁线构造体素化空间距离场,再对点阵结构梁线抽取等值面来生成点阵结构,见图3b。相比于方法1,方法2生成的点阵结构的节点更加饱满,杆与杆之间的过渡更加平滑,因此减少了节点的应力集中,提高了点阵结构的力学性能[20]。本文选择方法2构造点阵结构,该方法主要分为3个步骤:①构造距离场函数模型;②对梁线体素化并计算每个体素的距离场函数值;③利用Marching Cubes算法对体素化空间抽取等值面,生成点阵结构。如图3c所示,点阵的曲面模型由许多体素组成,体素(图3d)是最小组成单元,其中心到每根梁的距离为距离函数值。由于距离函数值相同的体素在同一个曲面上,因此对体素化空间抽取等值面便可获得点阵结构。
(a)方法1生成的点阵结构 (b)方法2生成的点阵结构
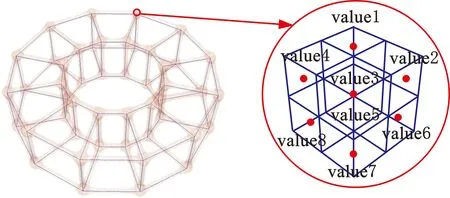
(c)点阵结构的曲面模型 (d)体素图3 构造点阵结构的方法Fig.3 The method of constructing lattice structure
为获得体素的距离场函数值,将体素记为点N,其坐标记为(x,y,z),将梁线记为L。点N到L的距离为该体素的距离函数值。L的2个端点记为起点S和终点E。如图4所示,点N与L有3种空间位置关系,不同的空间位置关系有不同的点到线的距离计算公式。因此,这里通过下式来判断点N与点L的空间位置:
t=[(xS-xN)(xS-xE)+(yS-yN)(yS-yE)+
(zS-zN)(zS-zE)][(xS-xE)2+(yS-yE)2+
(zS-zE)2]-1
(1)
式中,t为判断参数,(xS,yS,zS)、(xE,yE,zE)、(xN,yN,zN)分别为点S、E和N的坐标。
t<0时,点N到线L的距离为点N到点S的线段长度(见图4a);0≤t≤1时,点N到线L的距离为点N到线L的垂线段长度(见图4b);t>1时,点N到线L的距离就是点N到点E的线段长度(见图4c)。因此,计算点N到线L的距离公式为
d(N,L)=
(2)
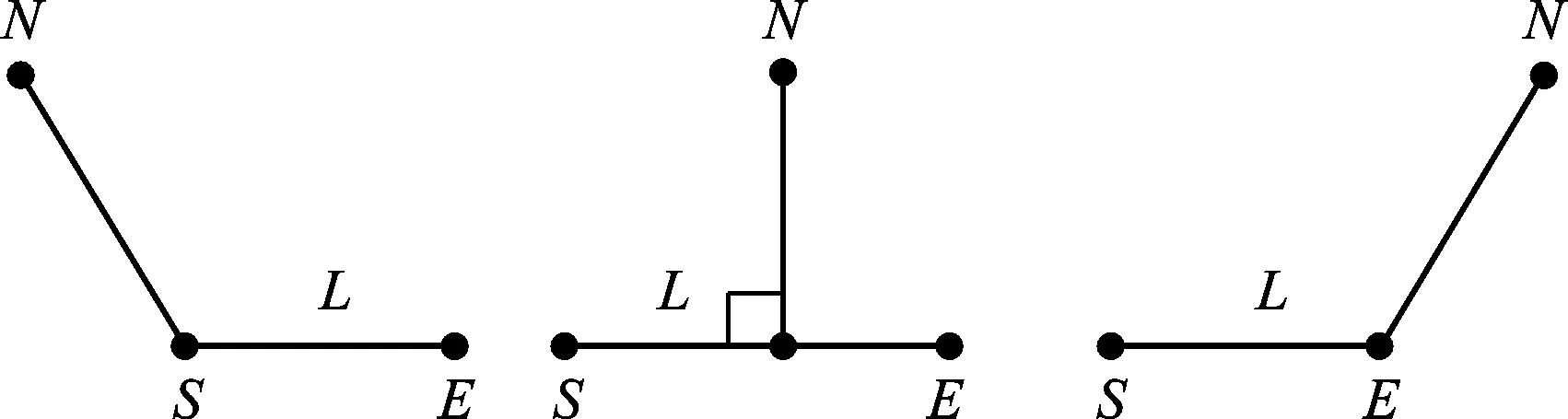
(a)t<0 (b)0≤t≤1 (c)t>1图4 体素与梁线的空间位置Fig.4 Spatial position of voxels and beams
于是,体素化空间距离场函数模型为
(3)
式中,Nx、Ny、Nz分别为包围盒沿X轴、Y轴、Z轴划分所得到体素的数量。
如表1所示,改变距离场函数值可以改变点阵胞元的节点半径和杆径。
1.4 节点参数化调控
杆结构的连接处存在应力集中,因此节点往往被视为点阵最薄弱处。由点阵结构的细观力学模型[11]可知,增大节点半径可提高点阵强度。本节提出的参数化调控方法根据给定工况对点阵的梁模型进行有限元分析,并依据其分析结果增大强度不足的节点半径,从而实现点阵整体强度的提高。节点半径由参与调控的节点体素的距离场函数值及参与调控的节点体素的数量决定。点阵
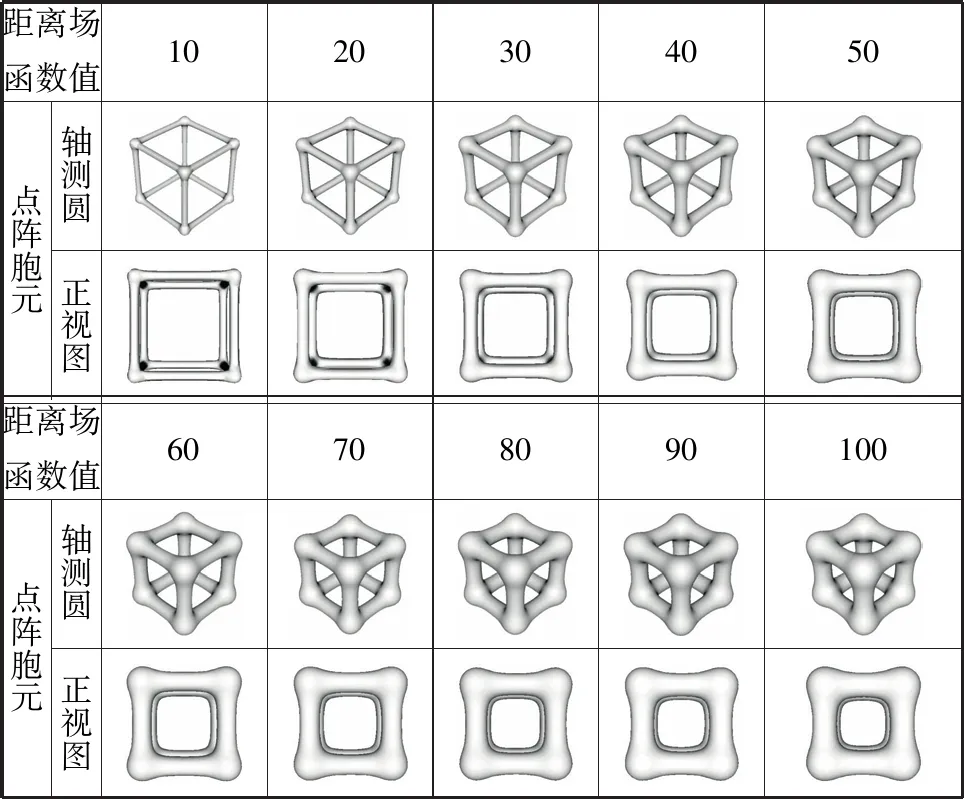
表1 距离场函数值对点阵胞元的影响
模型的体素化信息可表示为(I,x,y,z,V),其中,I为体素号,(x,y,z)为体素坐标,V为距离场函数值。梁模型仿真结果中,节点分析的结果表示为(I,x,y,z,F),其中,F为梁节点的变形量。实现梁模型仿真结果对点阵体素的调控的具体算法如下。

算法1:计算节点半径的增大倍数输入:(I,x,y,z,F)。输出:(I,x,y,z,w)。1. for i ← 1 to n∥n为点阵的节点数量2. wi=1 +(Fi-Fmin)/(Fmax-Fmin)∥w为梁模型节点的半径增大倍数,将节点半径增大至与其变形量匹配的倍数,从而对点阵结构进行补强3. end for4. ∥仅增大存在破坏风险的节点的半径5. for i ← 1 to n∥n为点阵的节点数量6. if Fi < Frisk∥ Frisk为梁模型仿真中存在破坏风险的节点的变形7. wi=18. else if9. wi=wi10. end if11.end for

算法2:利用八叉树调控节点体素输入:(I,x,y,z,V)、(I,x,y,z,w)。输出:(I,x,y,z,R)。1. for i ← 1 to m∥ m为点阵体素的数量2. voxel_octree ← voxel[i].(x, y,z)3. end for4. for i ← 1 to n∥ n为点阵的节点数量5. Query ← w[i].(x,y,z)∥ Query为当前查询的节点坐标

6. Ri=wi ∗ R0∥ R0为初始节点半径7. Function FindPointsWithRadius(Ri, Query, result)∥以Ri为查询半径在voxel_octree中查找参与调控的节点体素,并将查询结果放入result中8. for i ← 1 to k∥k为result的数量9. map[i]← result[i].(x,y,z)10. end for11.end for12.for i ← 1 to h∥h为参与调控的节点体素的数量13. map_octree ← map[i].(x,y,z)14.end for15.for i ← 1 to m∥ m为点阵体素的数量16. Query← voxel[i].(x,y,z)∥Query为当前查询的体素坐标17. I=FindClosestPoint(Query)∥在map_octree 中查找需要调控的体素,I为查询到的体素18. if I=0∥未查询到则该体素的距离场函数值不变19. Ri=Vi20. else if∥查询到则修改该体素的距离场函数值21. Ri=Vi ∗ map[i].w22. end if23.end for
2 实验设计
2.1 实验方法
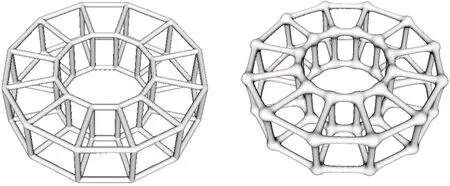
为验证所提方法的有效性,本节以齿轮为载体对辐板填充功能点阵结构,并通过振动实验和承载实验验证点阵结构的功能特性和承载能力。实验齿轮样件的齿数为24,模数为6,内部填充点阵结构的辐板外圆、内圆的直径分别为119 mm和54 mm,以光敏树脂为材料,采用光固化成形工艺制造。如图5所示,针对辐板的内外圆环面设计出共形点阵梁线,通过有限元模拟齿轮的振动工况,得到梁模型的振动仿真结果(图5a)。通过对共形梁线构造体素化空间距离场并抽取等值面,得到共形点阵(图5b)。为降低共形点阵齿轮的振幅,依据梁模型的振动仿真结果对共形点阵中强度不足的节点进行参数化调控,得到功能点阵(图5c)。相比共形点阵,节点增强后的功能点阵质量有所增加,因此,为客观评价功能点阵的功能特性,通过等比例增大共形点阵体素的距离场函数值,得到质量与功能点阵基本相同的增强型共形点阵(图5d)。上述点阵齿轮的质量与转动惯量如表2所示。
对实心齿轮S和共形点阵齿轮G组成的齿轮副S-G、实心齿轮S和增强型共形点阵齿轮Q组成的齿轮副S-Q、实心齿轮S和功能点阵齿轮F组成的齿轮副S-F进行振动性能检测实验。为保证3种齿轮副具有相同的测试工况,采用手持型转速表对电机转速进行检测与调控。齿轮转速的检测方法如下:①将反光贴纸贴在电机输出轴上;②齿轮转动时,启动手持型转速表,发射出光束并将其始终对准电机输出轴;③从手持型转速表显示器读取齿轮转速。通过分析齿轮副啮合产生的振动信号,获得不同齿轮副的加速度频谱。加速度频谱中,主频振幅表征结构振动的最大变形,主频振幅越大,结构振动越剧烈。因此,以主频振幅为标准,评估点阵的振动性能。
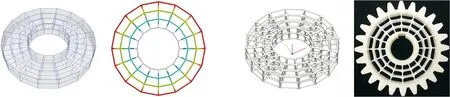
(a)共形梁线及其梁模型的振动仿真结果 (b)共形点阵

(c)功能点阵 (d)增强型共形点阵图5 实验齿轮样件Fig.5 Experimental gears

表2 不同齿轮的质量与转动惯量
承载能力检测实验中,以恒压频比的方式启动电机,以齿轮断裂时的电机变频器示数为标准,评估点阵的承载能力。
2.2 实验平台搭建
实验齿轮样件的振动性能由搭建的振动检测平台检测(图6a),该平台由传动系统(图6b)和信号分析系统组成。传动系统包括1根传动轴、1对轴承座、1台调频电动机、1个传感器和1对待测齿轮副。1对待测齿轮副的中心距等于单个齿轮的分度圆直径,以满足齿轮副的啮合要求。齿轮副的振动信号在传动系统中产生。利用PCB加速度传感器(型号8703450M1)采集待测齿轮副的振动信号,利用Spider-80XI模块处理信号,最后由Crystal软件将振动信号转换为加速度频谱。

(a)振动检测平台

(b)传动系统 (c)承载能力检测平台图6 实验系统搭建Fig.6 Experimental system construction
齿轮的承载能力在承载能力检测平台上检测(图6c)。该平台由传动系统改装而得,即将传动系统的传动轴更换为固定轴后,在固定轴上安装金属齿轮。电机驱动待测齿轮转动时,固定金属齿轮不动,与其啮合的待测齿轮也无法转动,此时的电机转速为0,转差率为0,待测齿轮承受的是电机的启动扭矩。变频器以恒压频比的方式启动电机,增大电机频率可增大施加在待测齿轮上的扭矩,从而增大轮齿上的法向力。当法向力达到轮齿的极限载荷时,待测齿轮发生破坏。实验过程中,轮齿上的法向力随电机频率的增大而增大,因此,通过对比齿轮破坏时的电机频率,可对比点阵的极限载荷,进而对比其承载能力。
3 实验结果
3.1 振动实验
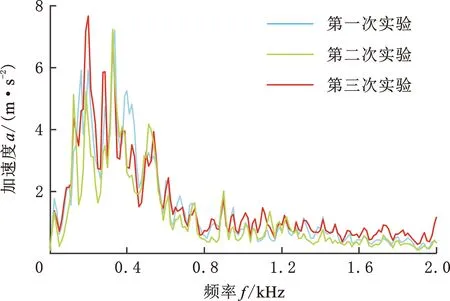
在电机的不同转速下对3种齿轮副进行振动测试,测试结果如表3所示。电机转速为80 r/min时,功能点阵的主频振幅下降最多,下降了33.60%。
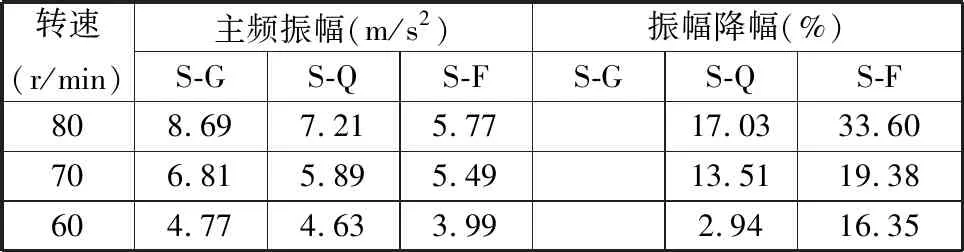
表3 不同电机转速下的振动实验结果
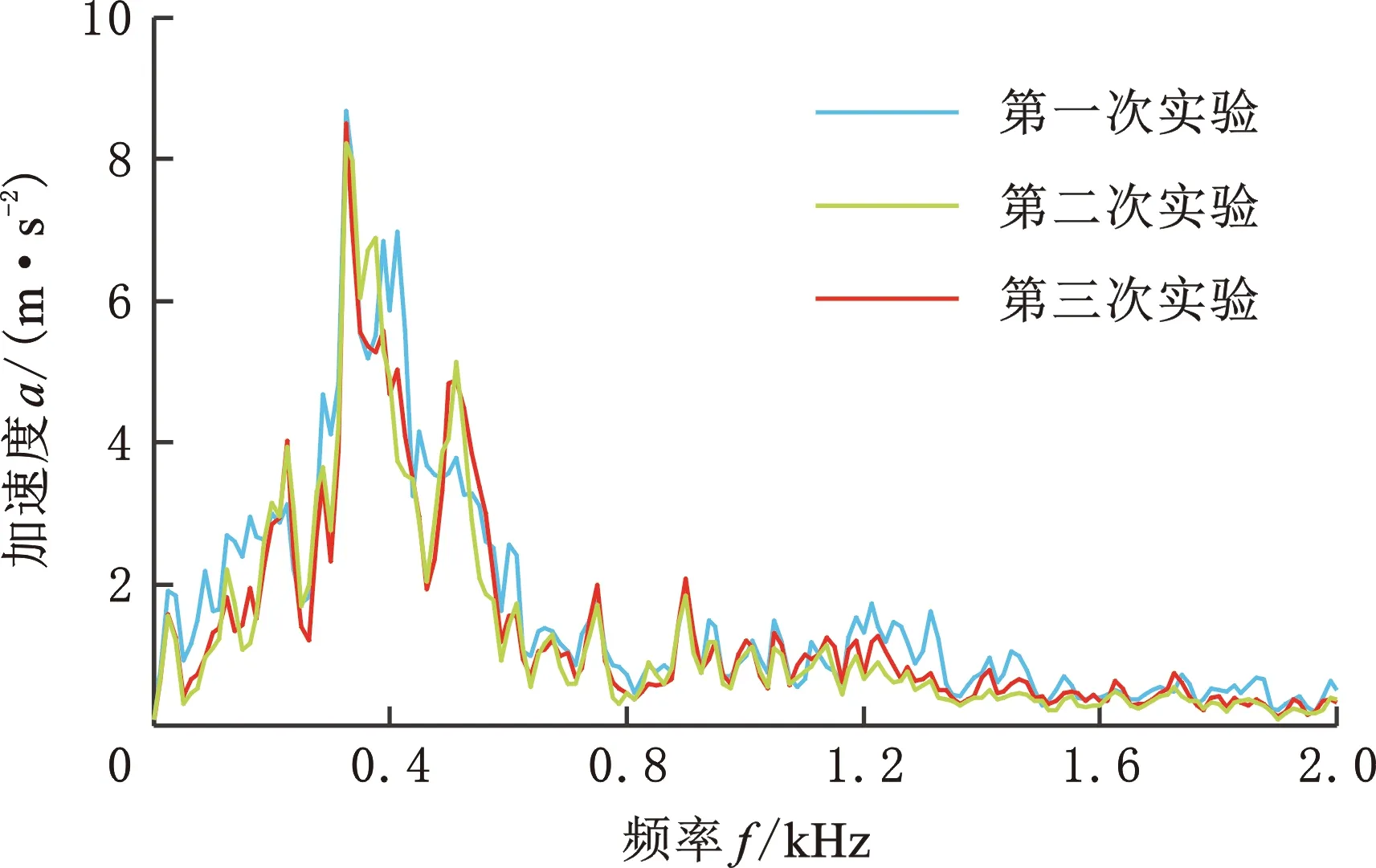
电机转速为80 r/min时,重复3次振动实验,3次振动实验中的所有齿轮副的加速度频谱如图7所示。实验结果如表4所示。增强型共形点阵和功能点阵的质量基本相同,但后者减振效果更好(相比前者,后者的主频振幅下降了20.90%)。
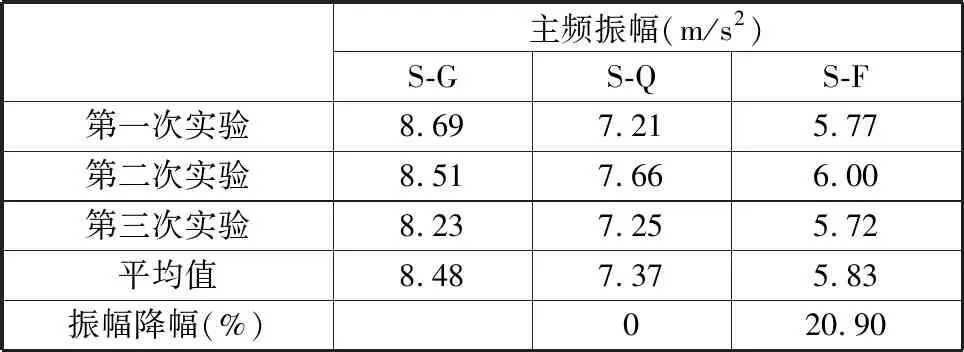
表4 80 r/min下的不同齿轮副的主频振幅
3.2 承载实验
采取有限元仿真及齿轮承载实验来验证功能点阵的承载能力。有限元仿真模型的网格在3-matic软件中划分,网格尺寸为1 mm,网格单元为四面体单元,约束设置为轮毂内表面固定,载荷为垂直于轮齿齿面的100 N法向力,加载位置在齿轮分度圆处,如图8所示。有限元仿真模型中,材料密度为1.16 g/cm3,弹性模量为2.5 GPa,泊松比为0.41。
不同点阵的应力分布与破坏情况如图9所示,承载实验结果如表5所示。由图9可知,共形点阵的杆结构存在密集的高应力区域,最大应力为14.70 MPa;增强型共形点阵杆结构的应力集中仍然存在,最大应力为6.25 MPa;功能点阵杆结构的应力集中有所减少,最大应力为5.76 MPa。
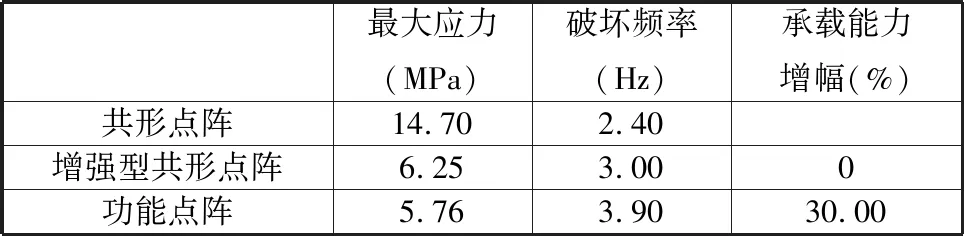
表5 承载实验结果
(a)齿轮副S-G
(b)齿轮副S-Q

(c)齿轮副S-F图7 3次振动实验中的3种齿轮副的加速度频谱Fig.7 Acceleration spectrum of three kinds of gear pairs in three times vibration experiments
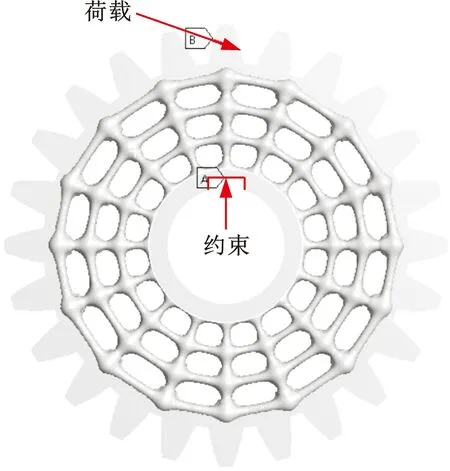
图8 点阵结构的承载有限元模型Fig.8 Finite element model of lattice in loading experiment

(a)共形点阵

(b)增强型共形点阵
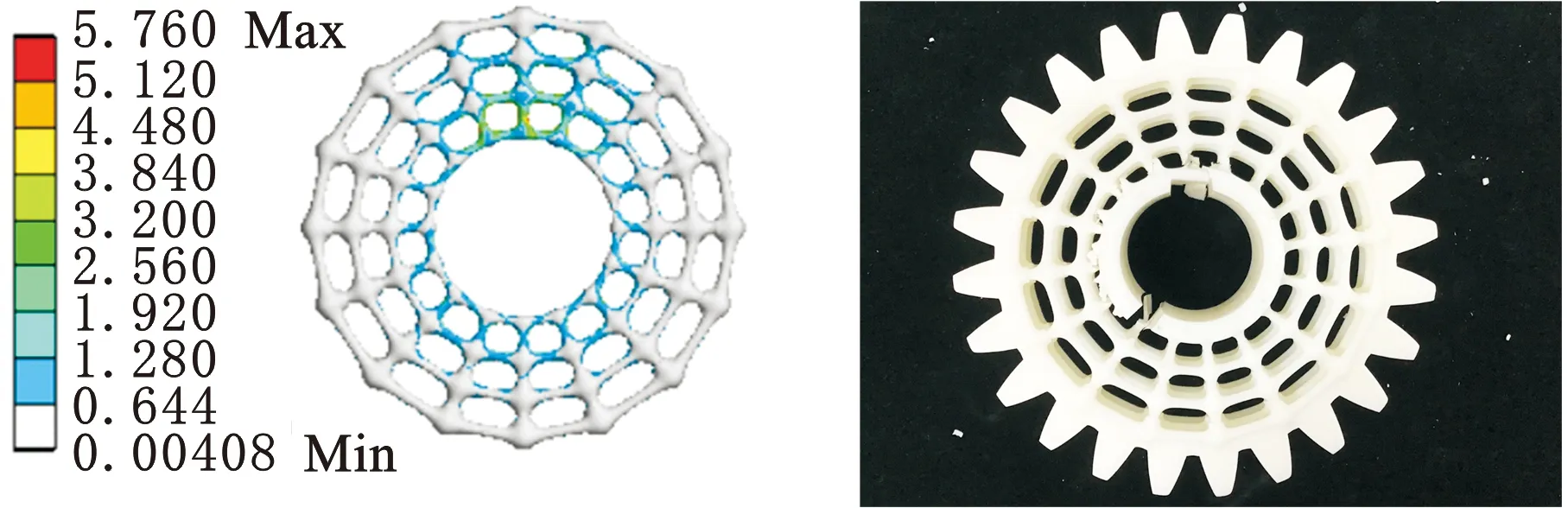
(c)功能点阵图9 不同点阵的应力分布与破坏情况Fig.9 Stress distribution and fracture of different lattices
由破坏情况和承载实验结果可知,共形点阵破坏时,其最内圈的所有杆结构断裂,点阵与轮毂分离,破坏时的电机频率为2.4 Hz;增强型共形点阵破坏时,部分杆结构随轮毂和轮齿一起断裂,其余杆结构保持完整,破坏时的电机频率为3.0 Hz;功能点阵破坏时,最内圈的少数杆结构随轮毂一起断裂,大部分杆结构保持完整,破坏时的电机频率为3.9 Hz。增强型共形点阵和功能点阵的质量基本相同,而功能点阵的承载能力更好,破坏频率较增强型共形点阵提高了30.00%。
4 结论
(1)依据梁模型的振动仿真结果对强度不足的节点进行参数化调控,可在保证点阵结构自身轻量化效果的同时降低点阵结构的振幅。
(2)依据梁模型的振动仿真结果对强度不足的节点进行参数化调控,可减少周围杆结构的应力集中,使点阵的承载能力得到充分发挥,从而能够抵抗较大载荷。
(3)对比质量相同的点阵结构,功能点阵的主频振幅降低了20.90%,承载能力提高了30.00%。
