V型波纹夹层板弯曲问题的高阶剪切变形理论计算方法

王小明，潘 曼，魏 强，2

（1.中国舰船研究设计中心，武汉430064；2.船舶振动噪声重点实验室，武汉430064）

0 引 言

夹层板不仅具有比强度高、比刚度高的优点，还具有吸声隔振的效果，一直以来就是工程关注的焦点和科学研究的热点。夹层板中的芯层可设计性非常强，可以是PVC泡沫、玻璃纤维、金属薄片等，这种特点为夹层板的工程应用提供了更多选择。其中，金属薄片又有很多的形式，可以是波纹型（V型）、I 型、Y 型、O 型、Z 型等。长期以来，面板与芯层的连接加工技术制约着金属夹层板的生产效率；近年来，工程师们将激光焊接技术应用到金属夹层板的生产制造中，使得金属夹层板的生产加工更加便捷精准。关于它的工程应用，人们对它充满期待，前景看好，航空航天、船舶海洋工程都是其应用的方向[1-2]。关于波纹夹层板的弯曲问题，在长期的研究探索中逐渐形成了两个研究方向：第一个研究方向是把波纹夹层板等效成正交异性板，然后按照正交异性薄板的弯曲求解；第二个研究方向是根据一阶剪切变形理论模型，分别计算上下面板的变形能和芯层的变形能，然后采用最小势能原理，列出波纹夹层板的平衡微分方程[3]。第一个研究方向中等效方式又可以分为两类：一类是运用变形等效或者能量等效的原理求解芯层的等效弹性模量或者等效刚度[4-9]，夹层板就等效成层合板，上下面板是各向同性板，芯层是正交异性板；另一类是根据芯层的实际形状，不需要单独求解芯层的等效参数，直接根据整体变形等效的方法求解整体弯曲刚度和剪切刚度[10-18]，夹层板整体等效成正交异性板。整体等效方式最为著名的是Libove等[11]的等效刚度方法，后来，Fung和Tan等在Libove的等效刚度法基础上，推导了Z 型、C 型和V 型夹层板的等效刚度[12-15]。Chang 等[19]采用了Libove 的方法计算出等效刚度后，研究了夹层板内力、变形与夹层板的截面参数之间的变化规律；Wang等[7]把波纹夹层板芯层看作正交异性体，采用“同外力，等变形”的方法分别求解了芯层三个方向的等效弹性常数，最后采用正交异性板理论计算了夹层板的位移，与有限元算法比较，差别小于5%。文献[20]提出波纹夹层板在垂直波纹母线的平面内，其抗剪刚度无限大，垂直于波纹方向平面内的抗剪刚度为有限值；在这一前提下，推导了波纹夹层板的弯曲微分方程，但是并未介绍如何计算垂直波纹方向平面内的抗剪刚度。实际工程应用中，为了达到理想的强度和刚度，必然会将波纹夹层板的整体厚度、上下面板厚度和芯层板厚度都增大，倘若夹层板的整体厚度达到厚板的范畴，则不能忽略芯层的抗剪作用，即不能采用经典薄板理论，也不能采用一阶剪切变形理论，因为一阶剪切变形理论不满足上下自由表面条件，这时，应该采用高阶剪切变形理论求解。目前，关于波纹夹层板弯曲问题的文献多数是采用正交异性薄板理论或者一阶剪切变形理论算法，采用高阶剪切变形理论求解方法的公开文献很少。对于大厚度的波纹夹层板弯曲问题，倘若不采用高阶理论算法，将导致计算误差偏大。因此，有必要研究大厚度波纹夹层板的高阶剪切变形理论求解方法，为工程设计和计算提供指导。本文提出一种“同外力，等能量”的等效方法计算波纹芯层等效弹性参数；求出等效弹性参数之后，把夹层板等效成层合板，应用高阶剪切变形理论，列出波纹夹层板的弯曲微分方程，应用傅立叶级数法求解该方程，最终确定变形和应力。

1 芯层等效弹性模量和泊松比

关于芯层等效弹性参数的计算方法很多，Bartolozzi[8-9]等推导的方法被诸多学者采用，在文献[8-9]中推导出的芯层为正弦曲线的波纹板的等效模量。Cheon 和Park 等[5-6]采用了“同外力，等能量”的等效方法推导正弦波纹的等效刚度。本文则采用“同外力，等能量”的等效方法推导V 形波纹的等效弹性模量和泊松比。波纹夹层板和坐标系如图1所示，x轴沿着芯层的母线方向，y轴沿着芯层的波纹方向，z轴垂直于xoy平面，指向下方；xoy平面位于夹层板芯层的中面。z＜0一侧的面板叫上面板，z＞0一侧的面板叫下面板。上面板厚度为tt，下面板厚度为tb，芯层板厚tc，芯层净高hc，芯层周期长度为lc，芯层半周期斜面边长为l。芯层倾斜面与面板夹角为θ。分析时，以x方向长度为单位长度作为研究对象。

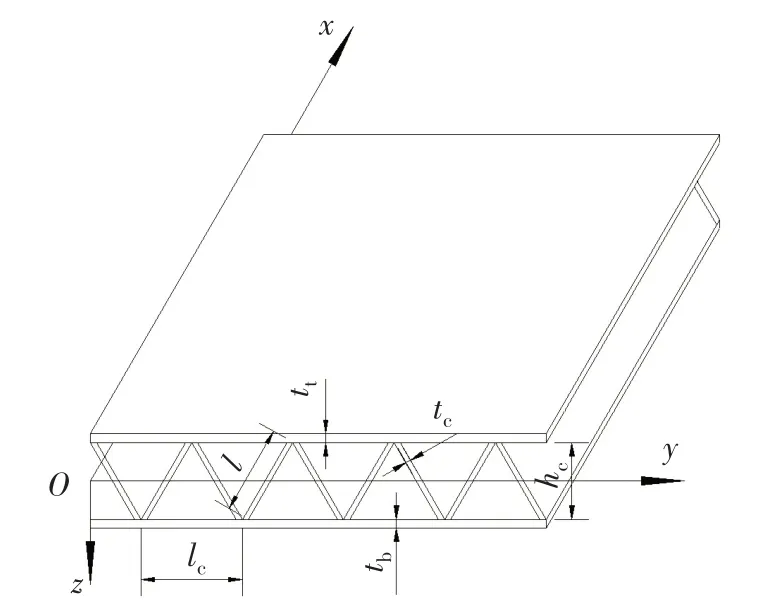
图1 夹层板与坐标系统Fig.1 Sandwich panel and coordinate system

1.1 yz平面等效模量

在夹层板芯层顶点施加一水平力F，顶点将发生微小的水平位移δ（如图2 所示）。将这个物理模型单独研究，选取其中的半单元芯层（图2中的①）进行分析，如图3 所示。为了保证芯层与纯剪切状态等效，则在芯层顶点加载水平载荷F时，芯层上方顶点（图3中的B点）不能有垂向位移，下方的顶点（图3中的A点）不能发生弯曲转角。这就意味着A点是固定铰支座，提供水平方向和竖直方向的支反力，B点是活动铰支座，仅提供竖直方向的支反力，简化后的物理模型如图3 所示。为了简化公式推导，把坐标系原点移到下方芯层顶点的位置，同时转换视角，以符合坐标习惯。

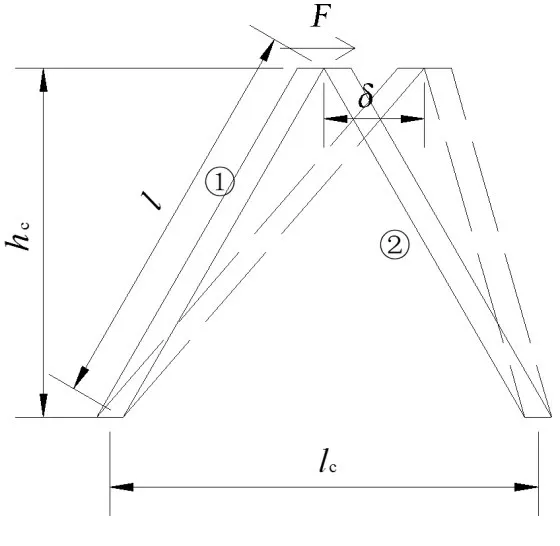
图2 芯层xz面剪切变形Fig.2 Core sheets shear deformation in xz plane

研究中认为，芯层沿x方向（垂直于纸面方向），长度为单位长度，根据芯层的平衡条件，容易求出下方顶点的位置处支反力R=Ftan(θ)。

根据图3的坐标系，容易得出芯层①中心线方程为

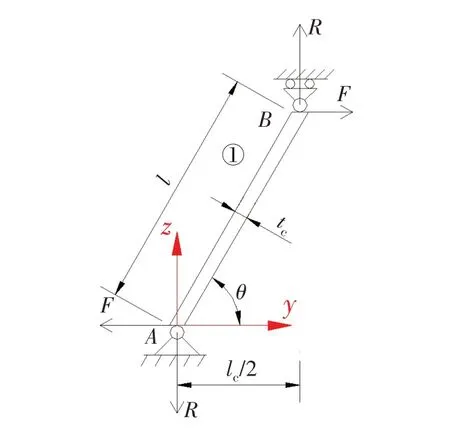
图3 计算力学模型Fig.3 Mechanics model for calculating

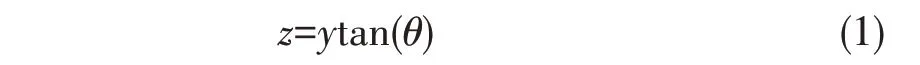
因为载荷作用在芯层上方顶点B的位置，则芯层的受力状态相当于二力杆，即芯层内力只有轴力，没有剪力和弯矩。

芯层①中的轴力（拉为正，压为负）表示为

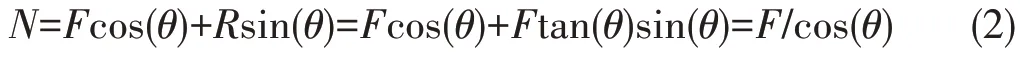
以上表明芯层中仅存在轴力，则芯层半单元中的总应变能为

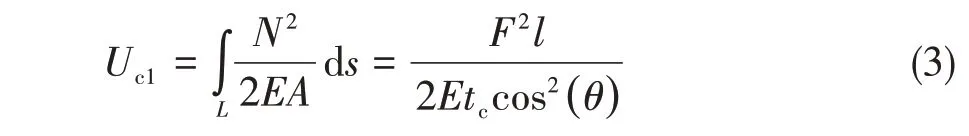
式中，L为半周期芯层横截面中心线，如芯层①的中心线，l为芯层①的长度，A为横截面面积，即A=tc。与芯层单元等效的模型如图4所示，则等效模型的应变能为

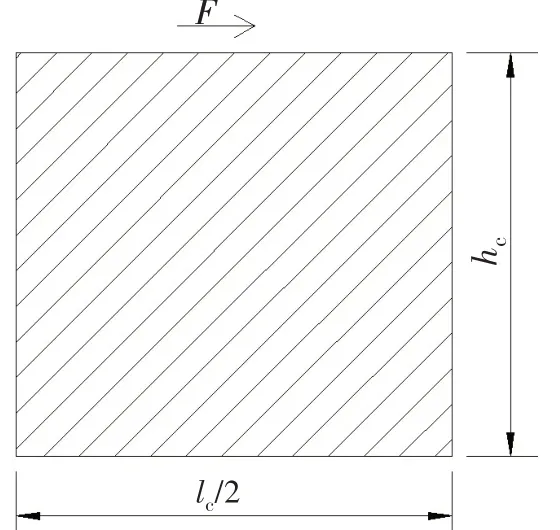
图4 计算等效均质模型Fig.4 Equivalent homogenous model for calculating

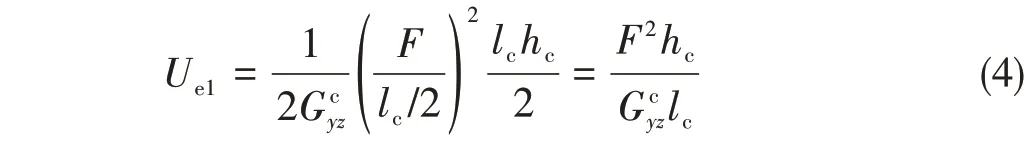
根据外力相等，应变能相等的原理，式（3）与式（4）相等，即可算出。

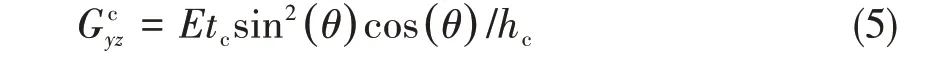
1.2 x方向等效弹性模量

均匀等效模型的应变能为

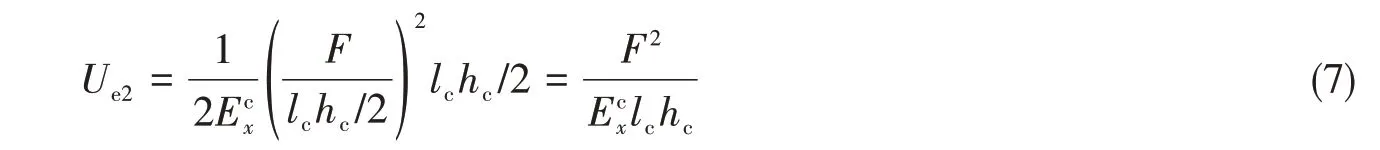
1.3 等效模量和

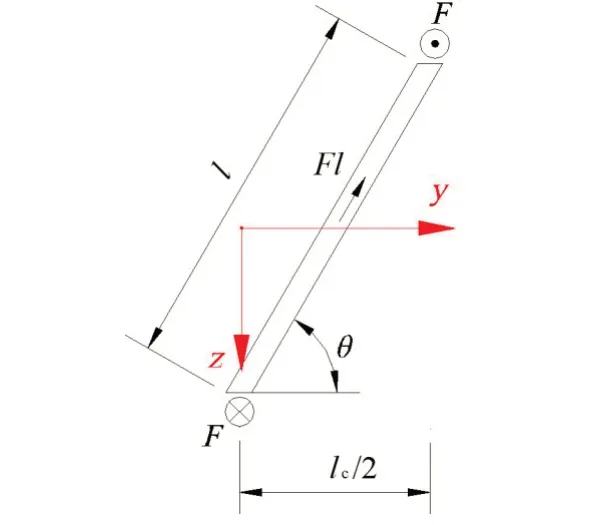
图5 计算力学模型Fig.5 Mechanics model for calculating

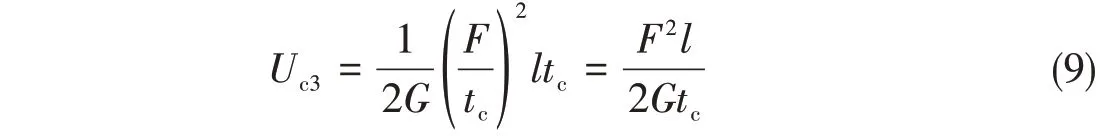
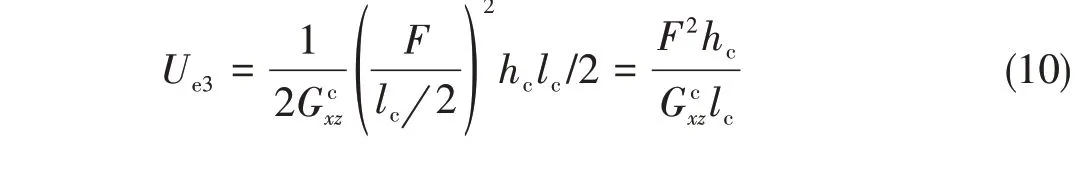
原模型与等效模型具有相同的剪切应变能，即式（9）与式（10）相等，求出。

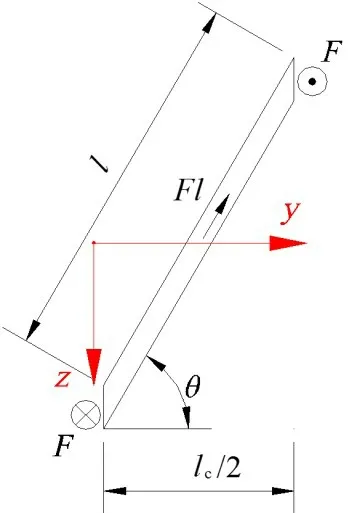
图6 计算力学模型Fig.6 Mechanics model for calculating

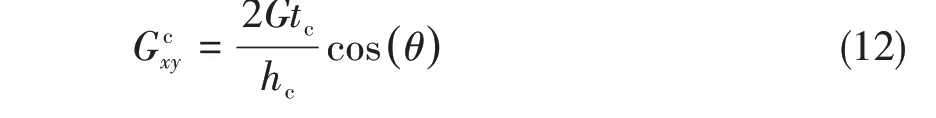
1.4 y方向等效弹性模量

设想芯层和等效均质模型均受到弯矩M作用后在yz平面内弯曲（如图7和图8所示），则两者的弯曲应变能应当相等。夹层板芯层的应变能为

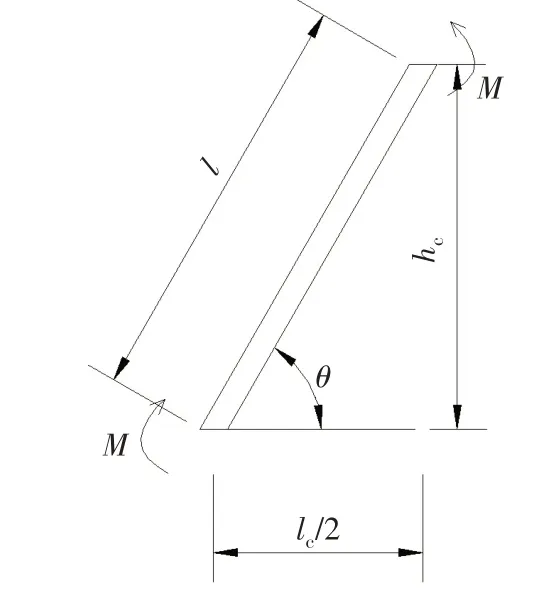
图7 计算力学模型Fig.7 Mechanics model for calculating

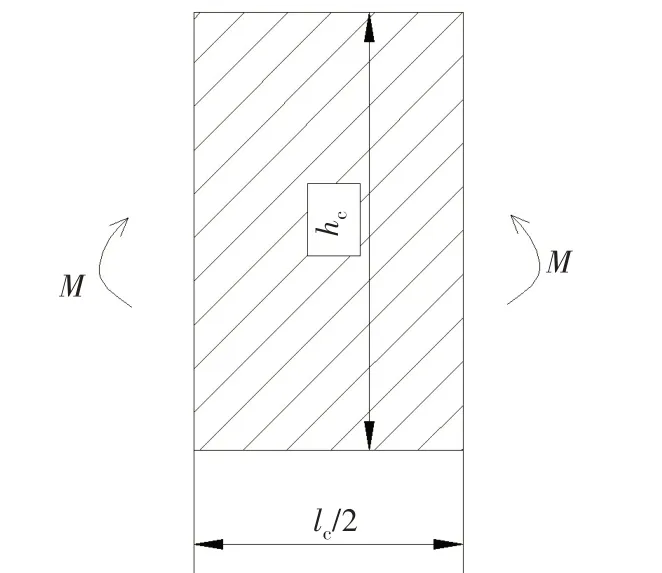
图8 计算等效均质模型Fig.8 Equivalent homogenous model for calculating y

等效均质模型的弯曲应变能为

根据变形能相等，即式（13）与式（14）相等，求出

1.5 泊松比和

1.2节中的受力状态正好是x方向受均匀拉力，则x方向的应变为

沿芯层倾斜方向的应变为

沿y方向的应变为

正交异性体弹性模量与泊松比满足方程

2 夹层板弯曲方程

2.1 位移模式

关于板的高阶理论有多种表达形式，本文采用Touratier提出的正弦函数表达式[21-22]。夹层板的坐标系统如图1所示，则夹层板的位移模式可以表示成

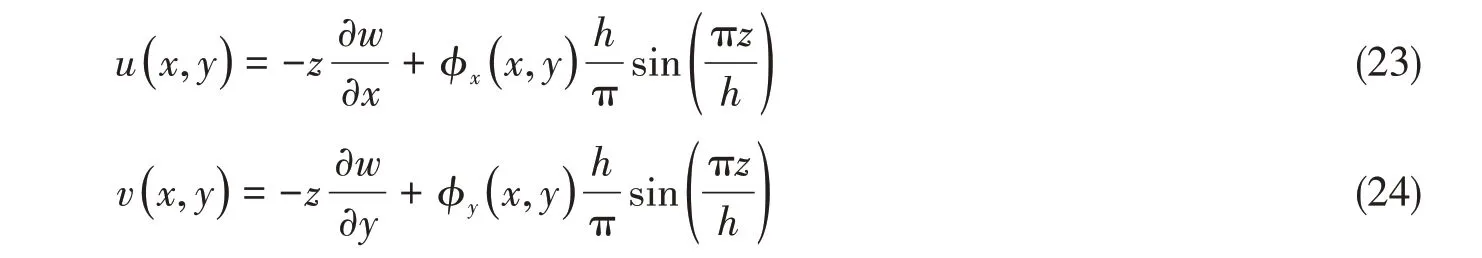
式中，h为整个夹层板厚度，即h=hc+tt+tb。

2.2 本构方程

夹层板的正应变和剪应变可以采用弹性力学几何方程表达式求解：

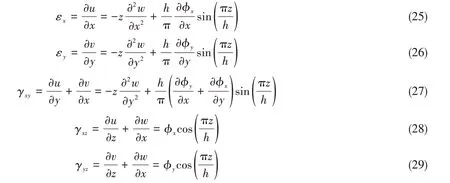
上下面板是各向同性板，本构方程直接采用各向同性体的胡克定律，上下面板的正应力和剪应力可以表示为

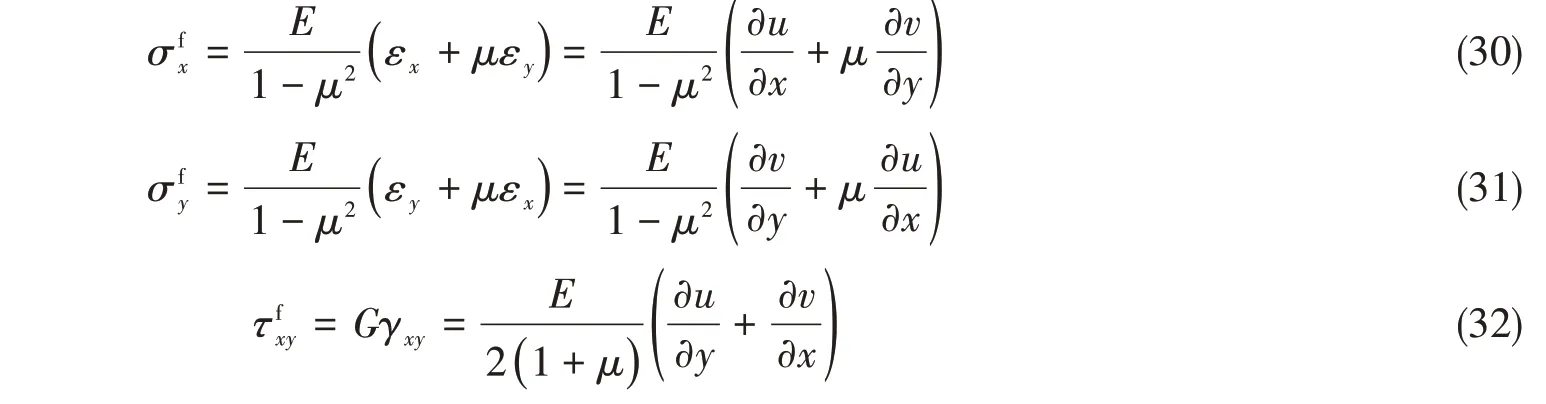
式（30）-（32）中，E、G和μ分别代表上下面板材料的弹性模量、剪切模量和泊松比。这里并没有考虑面板的横向剪应力是注意到上下面板处于远离中和轴位置，根据式（28）和式（29）计算的剪应变很小，可以忽略不计。

芯层等效为正交异性板，则其应力可以表达为

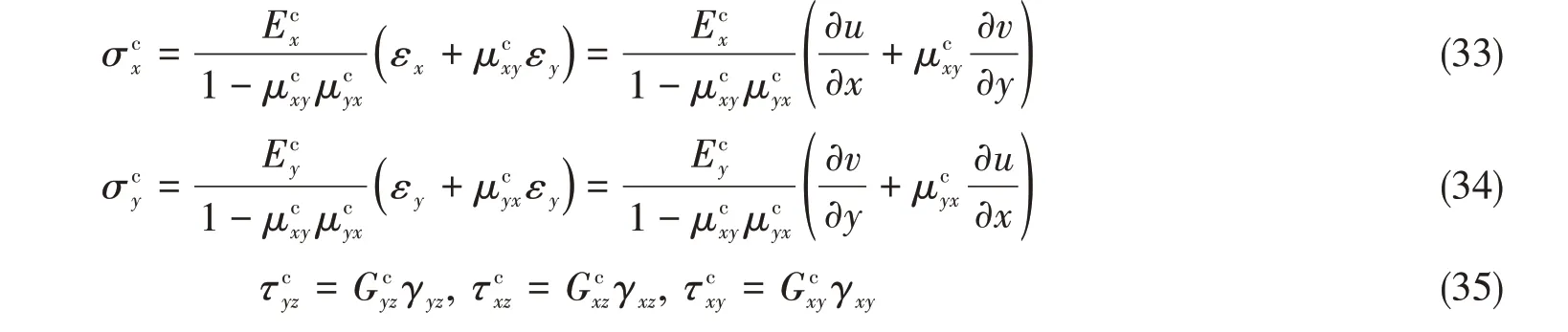
2.3 最小势能原理

根据最小势能原理，结构系统处于稳定状态，则它的位移必然使得整个系统的动势（动能与势能之差）达到最小值。对于夹层板的静力分析，则系统没有动能，仅有势能。势能包括两部分，一部分是系统的应变能，另一部分是外力的功。

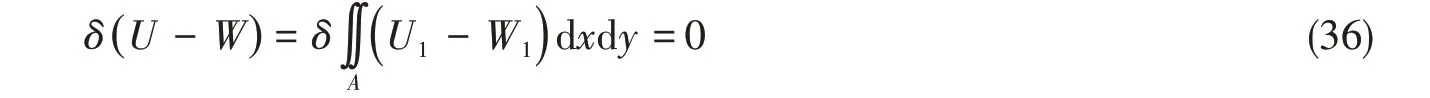
式中，A表示夹层板所在的xoy平面范围，U1和W1分别表示应变能面密度和单位面积上外力所做的功，δ表示变分。

系统的应变能包括三部分，分别是上、下面板应变能和芯层应变能。

其中，

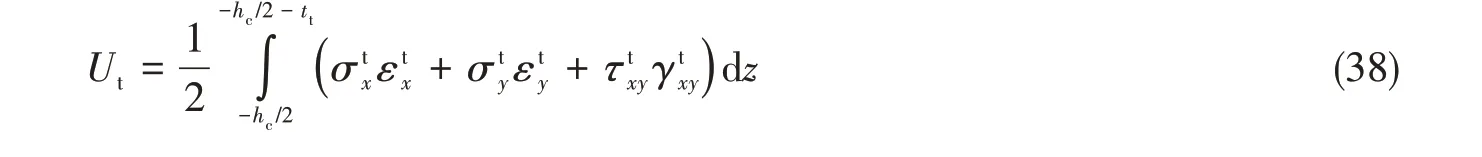
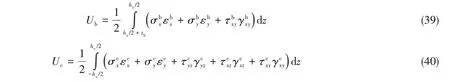
对于作用在坐标(x0,y0)的集中力，可以表达成为

式中，δ为狄拉克函数。

集中力所做的功为

对于式（36），根据变分法，令

则式（36）的欧拉方程为

系数A1、B1、C1等与夹层板的截面参数相关。该方程非常复杂，篇幅太长，不便于把系数表达式全部列出，在末尾附录A中给出了方程推导过程的Mathematica程序。

3 弯曲方程与求解

对于x方向长为a，y方向长为b的四边简支的夹层板，边界条件为

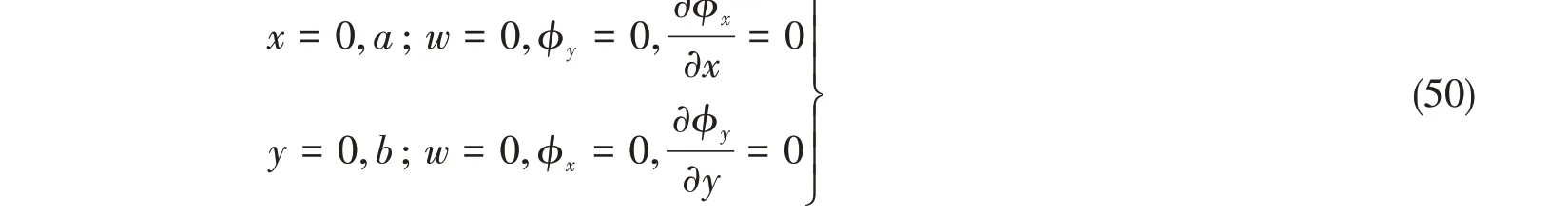
可以设方程（47）-（49）的解为双傅立叶级数形式

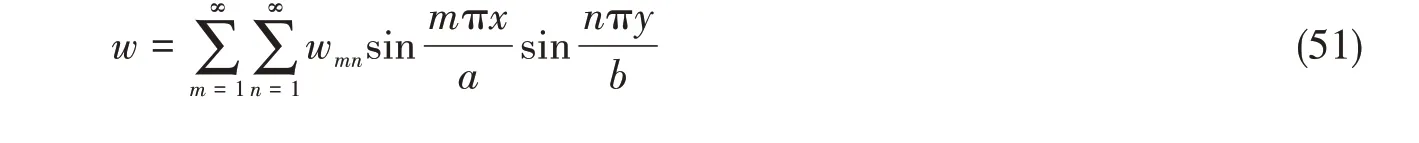
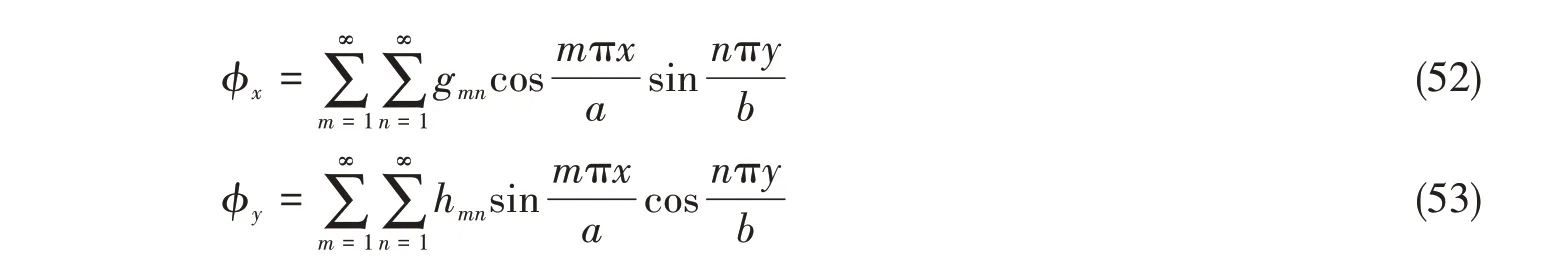
其实，式（51）-（53）已经满足了式（50）的边界条件。

集中力P作用点的坐标为（x0，y0），可以把集中力展开成双傅立叶级数：

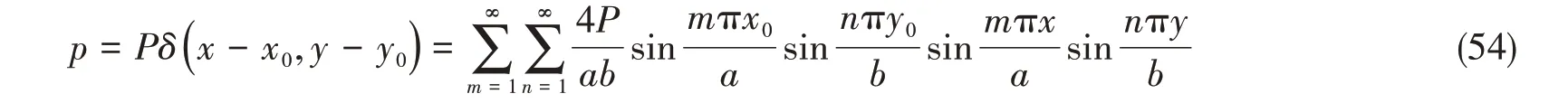
将式（51）-（54）代入式（47）-（49），然后比较两边的系数，可以分别求出上述式（51）-（53）中双傅立叶级数的系数wmn、gmn和hmn。

4 夹层板的应力

求出夹层板的变形之后，还需要继续求解夹层板的应力。

将第3章中求出的三个未知函数ϕx、ϕy和w对应代入到式（30）-（32）中则可以求出夹层板上下面板的应力。

芯层的实际应力则不能直接由式（33）-（35）求出，也没有方法准确求出，这是等效方法的共同点。夹层板弯曲问题，最大正应力一定出现在上下面板上。

5 算例与讨论

5.1 薄板模型

夹层板四边简支，长边a=2000 mm，短边b=1500 mm，上下面板厚度tt=tb=3 mm，芯层板厚度tc=2 mm，芯层净高度hc=40 mm，芯层周期间距lc=50 mm，上下面板和夹心都是同样材料，弹性模量E=Ec=2.1×105MPa，泊松比μ=0.3。集中力作用于上面板的中心点，作用点的坐标为（1000,750），集中力的大小为P=2×104N。计算模型即为在图1的基础上增加四边简支边界条件和板中心增加集中力作用。

为了形成对比，验证方法的准确性，分别用2种方法计算这个算例。方法1：本文计算方法，双傅里叶级数的项数迭代到m=n=15，此时位移和应力（远离载荷作用点的应力）均收敛；方法2：ANSYS 有限元计算方法，面板和芯层都采用Shell 181单元，网格划分成19 200个单元。

构件的变形和强度是工程关注的焦点，最关注的则是最大变形量和最大应力，以及出现的具体位置。上述算例中，根据构件和载荷的对称性，最大变形和最大应力可能出现在板的中心点。位移的级数表达式（51）-（53）是收敛的，一般m、n分别取到5 之后则变化非常小。应力表达式（30）～（32）在集中载荷作用点附近是不收敛的，应力为无限大，这一性质与单层板是相类似的。因此不能试图去比较x=a/2和y=b/2位置处的应力分布。

上述2种计算方法的结果中y=b/2和x=a/2两个典型位置的位移分布如图9和图10所示；4个典型位置的应力分布如图11～14所示。

由图9和图10可以看出，上述2种方法关于位移的计算结果极为接近，误差普遍很小。图11和图13 中关于x向应力的分布，本文方法计算结果与有限元计算结果也吻合一致。图12 和图14 中关于y向应力的分布，本文方法是光滑曲线，而有限元计算结果则是周期振荡的曲线，本文方法正好是有限元方法振荡波峰的插值光滑连线。经过反复的试算发现，振荡的周期与网格尺寸没有关系，仅与夹层板的截面参数有关，并且振荡周期等于夹层板波纹芯层周期。

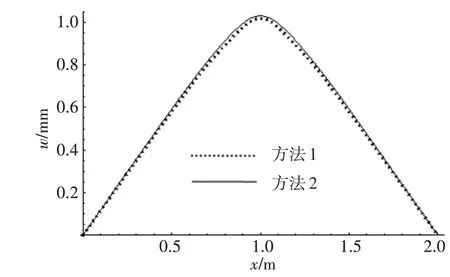
图9 y=b/2位置处的位移Fig.9 Deflection at y=b/2

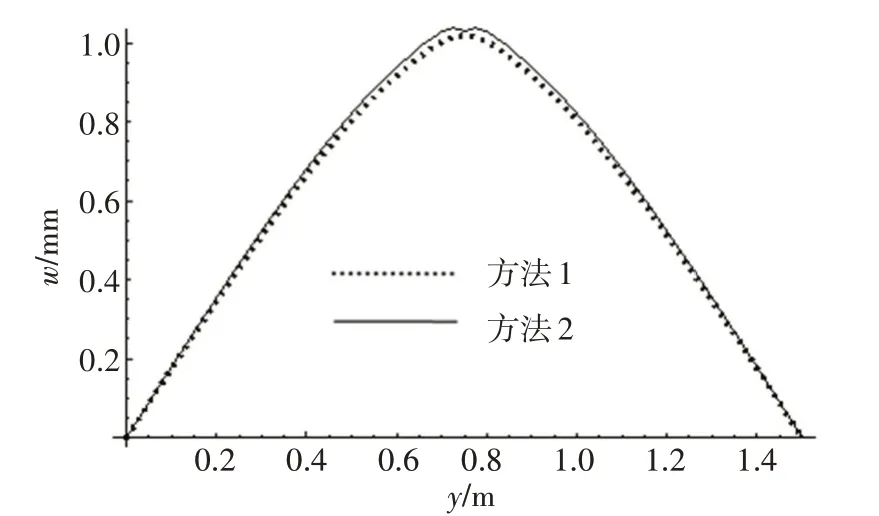
图10 x=a/2位置处的位移Fig.10 Deflection at x=a/2

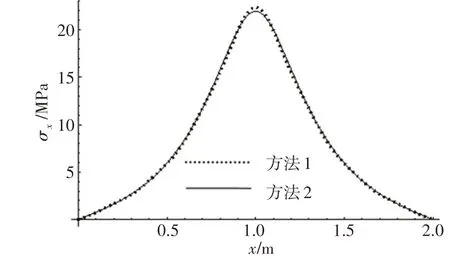
图11 y=b/3位置处下面板下表面x向应力Fig.11 x direction stress of bottom facesheet lower surface at y=b/3

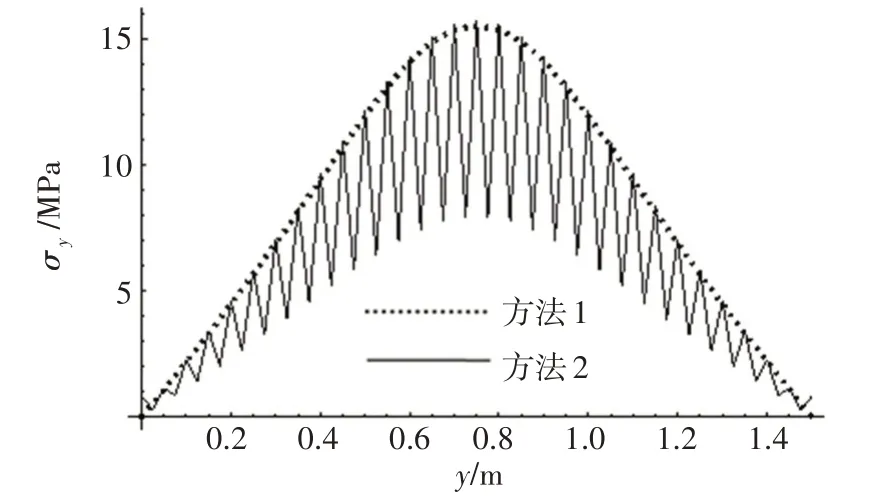
图12 x=a/4位置处下面板下表面y向应力Fig.12 y direction stress of bottom facesheet lower surface at x=a/4

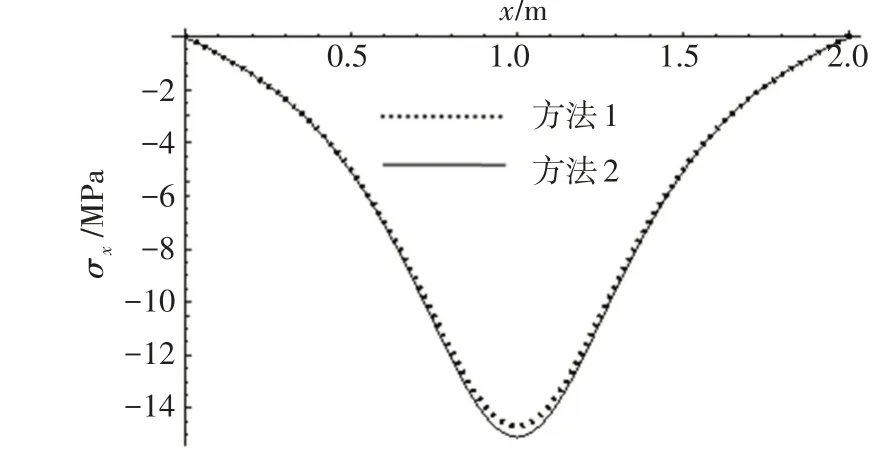
图13 y=b/4位置处上面板上表面x向应力Fig.13 x direction stress of top facesheet upper surface at y=a/4

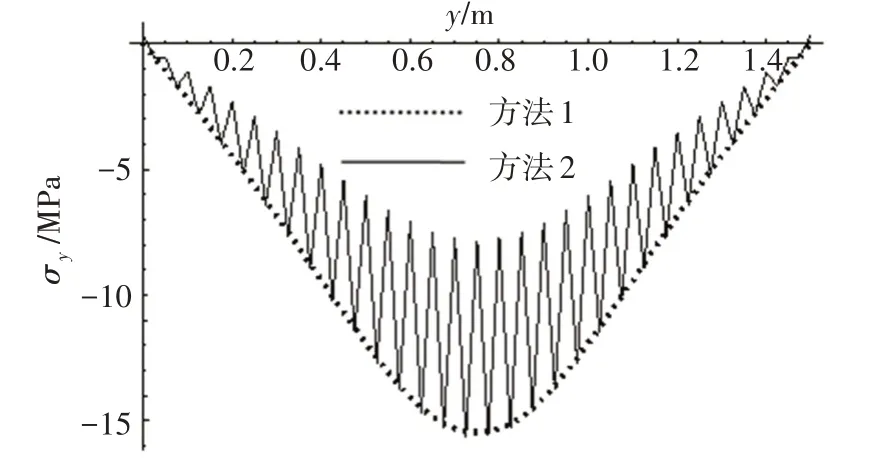
图14 x=a/4位置处上面板上表面y向应力Fig.14 y direction stress of top facesheet upper surface at x=a/4

实际上，x向应力随y坐标变化时，也表现出图12 和图14 的振荡特性，并且与图12 和图14 一样，面板与芯层顶点交汇的位置出现波峰，顶点中心的位置则出现波谷。这种振荡正是非连续芯层对面板的反作用力所致。

应力沿波纹方向分布表现出振荡性质，文献[3]也有相同的结论。目前解析法尚无法构造出夹层板的位移模型，使得其同时满足芯层板两侧的自由表面条件、上下面板的自由表面条件和芯层顶点与面板间的位移（应力）单值条件，因此解析法计算的结果也就不可能出现与有限元结果完全一致的振荡周期和振荡振幅。文献[3]中的载荷是均布载荷，文中采用了整体应力与局部应力叠加的方式计算上面板应力，即夹层板弯曲应力作为整体应力，两边芯层顶点固支板弯曲应力作为局部应力。均布载荷工况下，这种算法计算的上面板应力分布与有限元结果吻合一致。对于本文中集中载荷，这种方法则无法使用，因为集中载荷作用在芯层顶点时，局部应力不存在；倘若集中载荷作用点并非是芯层顶点，则仅一块局部板存在局部应力，也不能表现出周期振荡性质。对于下面板应力，上述叠加方法也是无效的，文献[3]并没有讨论下面板的应力，图12显示下面板应力沿波纹方向分布也存在振荡性质。

5.2 厚板模型

夹层板四边简支，长边a=2000 mm，短边b=1500 mm，上下面板厚度tt=tb=10 mm，芯层板厚度tc=8 mm，芯层净高度hc=300 mm，芯层周期间距lc=50 mm，上下面板和夹心都是同样材料，弹性模量E=Ec=2.1×105MPa，泊松比μ=0.3。集中力作用于上面板的中心点，作用点的坐标为（1000，750），集中力的大小为P=2×106N。

同样采用5.1 节中的2 种方法计算夹层板的位移，不过在方法1 中，为了保证应力的收敛性，双傅里叶级数的迭代项数更多，达到m=n=25。图15～20 分别列出了与5.1 节中薄板对应位置处的位移和应力分布。

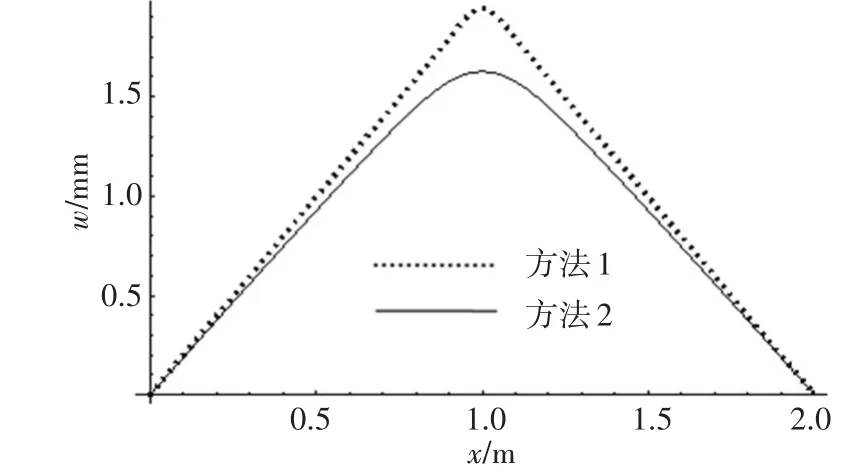
图15 厚板y=b/2位置处的位移Fig.15 Deflection of thick plate at y=b/2

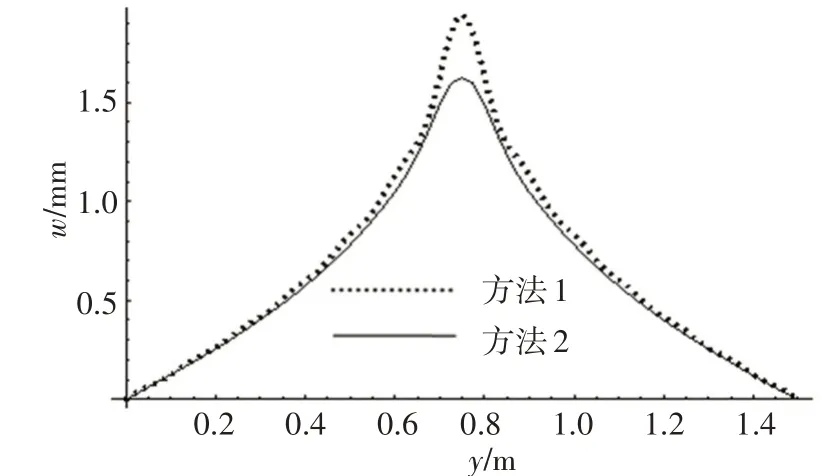
图16 厚板x=a/2位置处的位移Fig.16 Deflection of thick plate at x=a/2

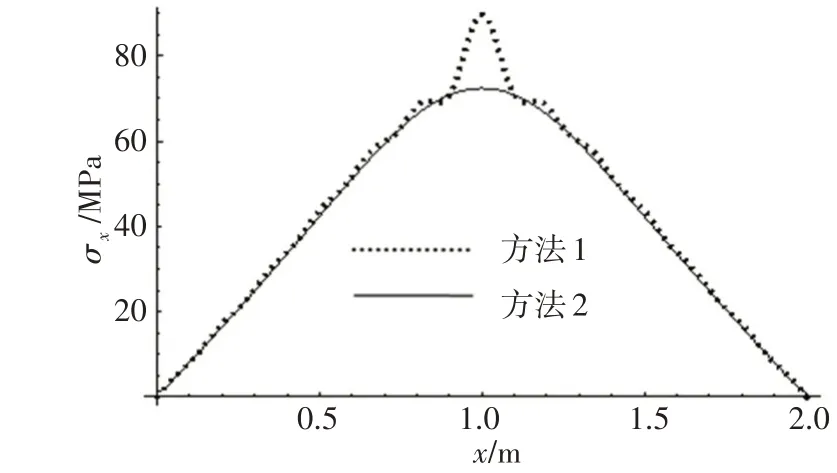
图17 厚板y=b/3位置处下面板下表面x向应力Fig.17 Bottom facesheet lower surface x direction stress at y=b/3 for thick plate

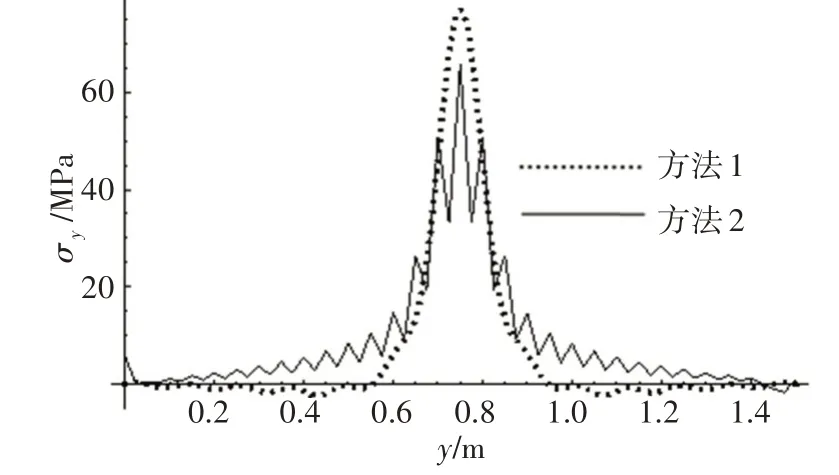
图18 厚板x=a/4位置处下面板下表面y向应力Fig.18 Bottom facesheet lower surface y direction stress at x=a/4 for thick plate

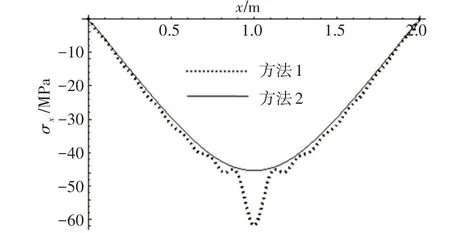
图19 厚板y=b/4位置处上面板上表面x向应力Fig.19 Top facesheet upper surface x direction stress at y=b/4 for thick plate

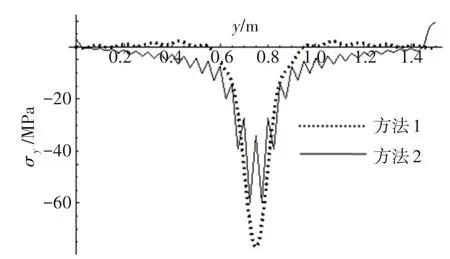
图20 厚板x=a/4位置处上面板上表面y向应力Fig.20 Top facesheet upper surface y direction stress at x=a/4 for thick plate

这一算例中，（hc+tt+tb）/b＞1/5，属于厚板的范畴。目前，商业有限元计算软件中，关于厚板的计算都采用一阶剪切变形理论，因此，方法2 是采用一阶剪切变形理论。在图15～20 中，2 种方法的计算结果已经不再保持薄板范畴的吻合状态。位移分布和x向应力分布在远离载荷作用点时，2种计算方法差别较小，越靠近中心，2种计算方法差别越大。y向应力则仅在少数位置点2种计算方法结果保持一致，多数位置差别较大。两种计算方法关于峰值有一个共同的特点：集中载荷作用下的厚夹层板，在平行于矩形板边缘的横剖面上，本文方法的位移峰值和应力峰值都比有限元结果偏大。

方法2沿波纹方向的应力分布依然表现出振荡性，其振荡的波幅仅在中心位置附近较大，远离中心则振幅很小。众所周知，厚板单层板弯曲问题需要采用高阶剪切理论或三维弹性理论计算，所以计算厚板波纹板弯曲问题也应当采用高阶剪切变形理论。以本文计算方法结果为基准，在上述算例中，有限元法位移峰值的差别为-16.3%，x向应力峰值差别为-26.6%，y向应力峰值差别为-55.4%。

6 结 论

本文通过将夹层板中间芯层等效成正交异性板，根据应变能等效原理求解芯层各项等效弹性模量和泊松比。运用高阶剪切变形理论和最小势能原理，推导夹层板的弯曲变形微分方程，然后采用双傅里叶级数的方法求解该微分方程。

通过算例验证，在薄板范畴内，本文方法计算的位移与有限元法结果吻合良好；本文方法计算的面板应力在芯层顶点位置与有限元一致，其他位置则比有限元结果偏大；由于波纹芯层与上下面板的相互作用，上下面板弯曲应力沿波纹方向分布表现出振荡性，越靠近外载荷作用点，振荡振幅越大，本文方法计算的应力分布恰好是有限元法结果中振荡波峰点的光滑连线。这一点对工程设计而言，计算结果是偏于安全的；这也说明薄板范围内的波纹夹层板，高阶剪切变形理论计算结果与一阶剪切变形理论结果是基本一致的。

通过算例验证，在厚板范畴内，集中载荷作用下的夹层板位移分布和x向应力分布在远离载荷作用点时，本文方法和有限元方法计算结果差别较小，越靠近中心，两种计算方法差别越大；y向应力则仅在少数位置点时本文方法与有限元方法结果保持一致，多数位置差别较大。在平行于矩形板边缘的横剖面上，对于位移和应力的分布峰值而言，本文方法结果普遍大于有限元结果。因此，在工程设计中，推荐采用高阶理论算法校核波纹夹层板的位移和应力。