基于惯量响应的双馈风电机组动态协调机理研究

刘櫂芮，贾祺，严干贵，翟文超，孙勇，李宝聚

(1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林 吉林 132012；2.国网吉林省电力有限公司，吉林 长春 130021)

0 引言

在实现 “碳中和，碳达峰”重要战略目标推动下，中国新能源发电呈快速发展趋势，其中以风电、光伏发电发展最为迅速，截至2021年9月，全国风电装机容量达3.0亿kW，预计到2050年，风电装机容量将达24亿kW[1]。

大规模风电联网给电力系统安全稳定运行带来挑战[2]，与同步机组具有转动惯量并主导系统频率不同[3-6]，风电机组经变流器联网，在最大功率点运行，不具备调频能力[7]，锁相环系统能够快速响应并追踪电网电压相位变化，不响应系统频率变化。为此，许多新能源发展迅速的国家均出台并网准则，要求新能源电站具备参与调频、惯性响应能力[8-12]。近年来，国内外学者主要围绕控制策略、频率响应特性分析开展研究工作。

控制策略方面，文献[13]提出将附加频率控制信号叠加在原有电磁功率指令上，使风机具有惯量。文献[14-17]提出释放或吸收风力机叶片中的动能，短时增发或减少功率响应系统频率变化。但文献[18]指出，转子转速恢复过程会导致频率二次跌落或升高。文献[19]提出引入恒定附加功率，使风机惯量响应期间维持转速至频率稳定再恢复，避免频率二次跌落。文献[20]提出风力发电应用虚拟同步控制技术，可实现惯量响应。以双馈风机为例，不过度提取风机转子动能，消除了频率二次跌落问题[21]。文献[22]通过优化风机虚拟同步参数配置，使其频率响应特性优于同步机组。频率响应特性分析方面，文献[23]在光伏发电单元机电暂态模型基础上，提出基于锁相环动态特性的虚拟惯量控制策略。文献[24]建立光伏发电单元频率响应模型，分析光伏发电单元惯量特性。但要注意由于并网结构及控制策略不同，双馈风电机组频率响应模型及惯量特性与光伏发电单元之间存在差异。

现有研究侧重于从策略层面实现风电机组惯量响应，对双馈风电机组（doubly fed induction generator, DFIG）自身惯量特性及对电网频率动态特性影响研究较少。实际系统中多采用双馈风电机组并联结构，把握不平衡功率在各个风电机组间分配机制是分析风电联网系统频率调节特性的关键。

本文基于双馈风电机组频率响应模型，解析得到双馈风电机组惯量表达式，并分析锁相环控制参数对机组惯量大小的影响，提出在系统功率扰动期间优化锁相环控制参数实现双馈风电机组惯量响应；以2台双馈风电机组并联系统为例，分析惯量响应期间不平衡功率在两机组间分配规律，并拓展到多双馈风电机组并联系统。建立双馈风电机组、同步机组联网系统频率响应模型，分析系统发生功率扰动各阶段频率响应特性。最后，搭建时域仿真验证了本文理论分析的正确性。

1 多双馈风电机组并联系统结构及控制策略

双馈风电机组并网系统结构如图1所示，由风力机、双馈感应电机、变流器、线路等构成[25]。图1中：Cdc为逆变器直流侧电容；Lcg为网侧变流器滤波电感；Lc为机组网侧线路电感；Lg为电网侧线路电感；Us、Ut和Ug分别为机端定子电压、并网点电压和电网电压；θs、θt和θg分别为三者相位。

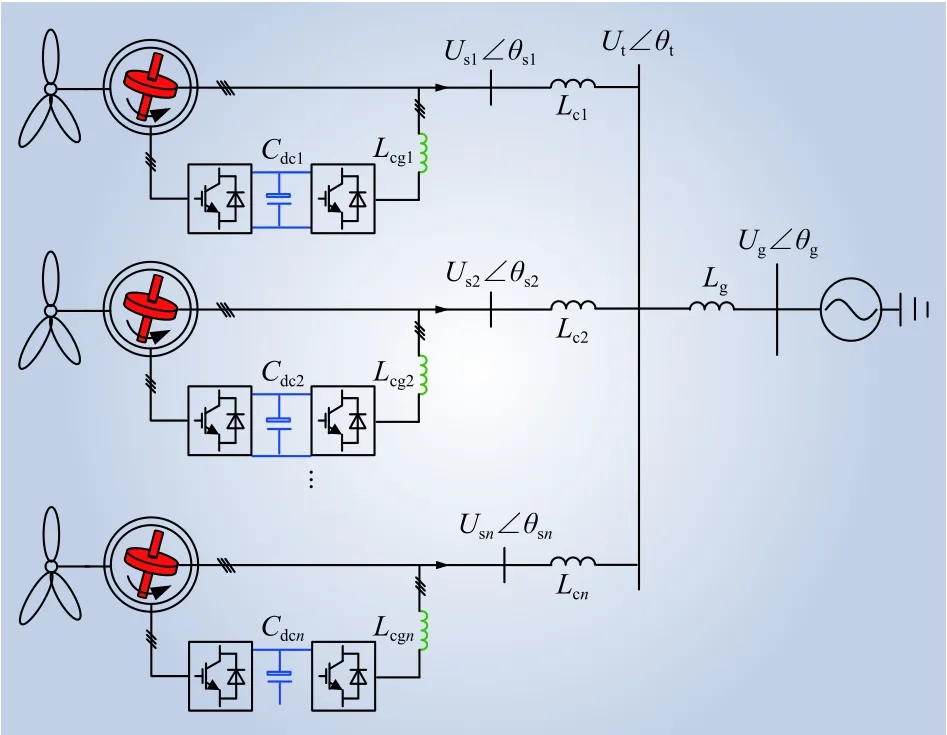
图1 双馈风电机组并联系统示意Fig.1 DFIG parallel system

dq坐标系下双馈感应电机定、转子电压方程为

式中：Usd/q、Urd/q分别为d、q坐标系下双馈感应电机定、转子电压；isd/q、ird/q分别为定、转子电流；Ψsd/q、Ψrd/q分别为定、转子磁链；ω1、ωs分别为同步角速度和转差角速度；Rs、Rr分别为定、转子电阻。

定、转子磁链方程为

式中：Ls、Lr、Lm分别为双馈感应电机定、转子自感及互感。

变流器采用dq解耦控制。转子侧变流器实现定子有功、无功控制；网侧变流器控制逆变器直流电压稳定并辅助转子侧变流器控制定子有功、无功功率，其基本控制框图如图2所示。

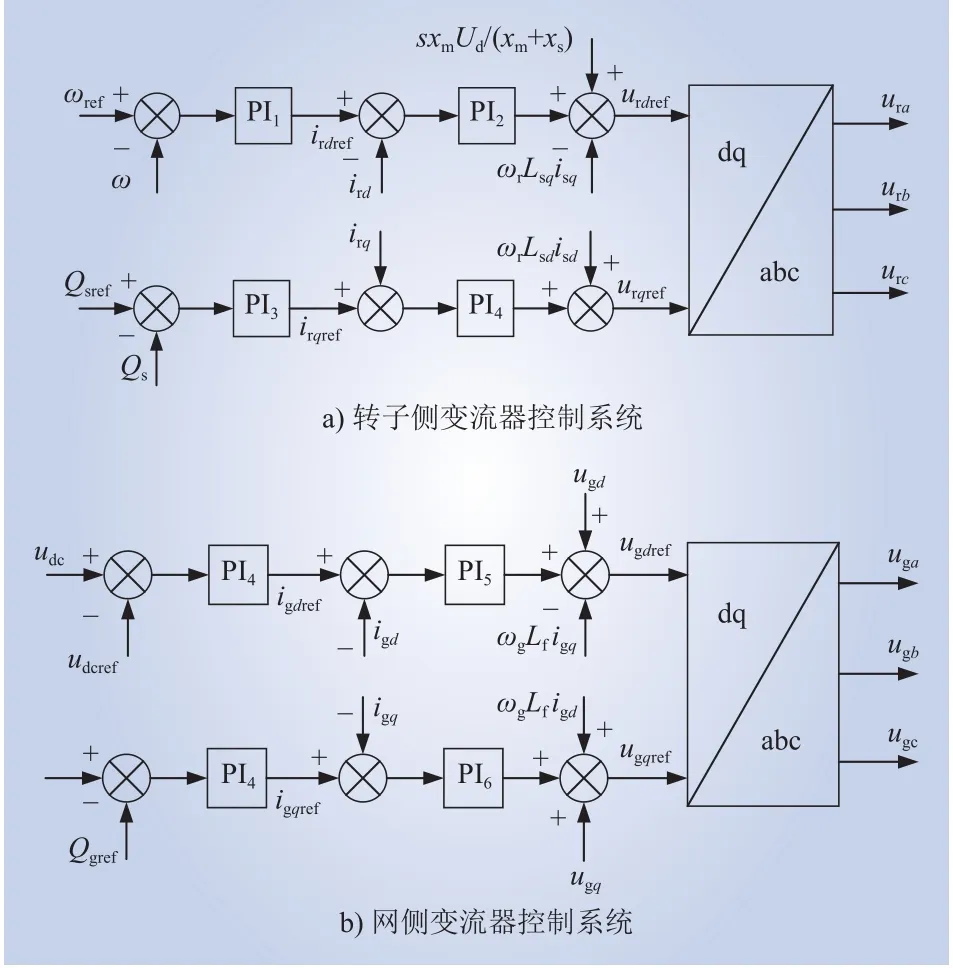
图2 双馈风电机组四象限变流器控制系统Fig.2 Four-quadrant converter control system of DFIG

2 双馈风电机组惯量特性

2.1 双馈风电机组频率响应模型

基于文献[26]提出的双馈风电机组频率响应模型，评估双馈风电机组惯量特性及其对系统频率特性影响。忽略电磁暂态过程，将式（1）（2）所示锁相环坐标系下定子电压、磁链方程简化为

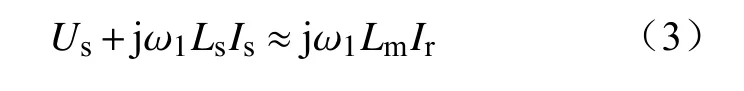
式中：Is、Ir分别为双馈感应电机定、转子侧电流矢量。

类比同步机组内电势概念，定义E=jωLmIr为双馈风电机组内电势，锁相环坐标系下，内电势E、电网电压Ug、双馈风机端电压Us以及受扰动后端电压相位U's三者相位关系如图3所示。

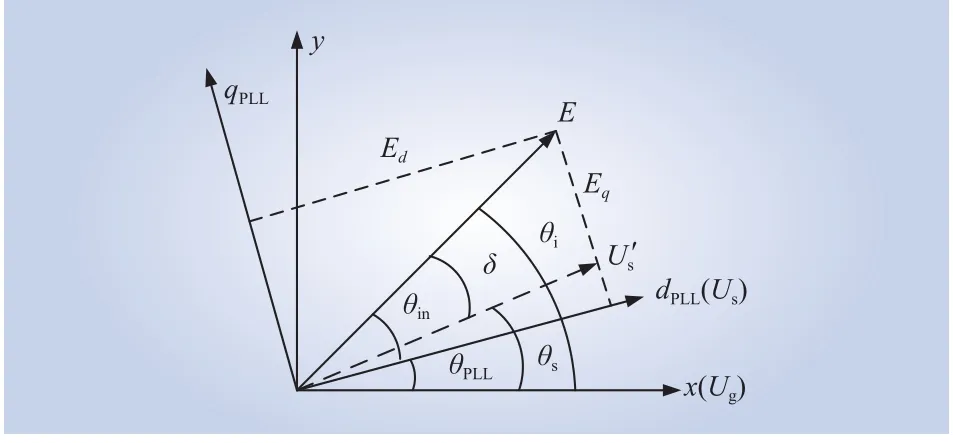
图3 锁相环坐标系下双馈风电机组内电势相位示意Fig.3 Internal potential phase of DFIG in PLL coordinate system

忽略风电机组无功控制环的影响，构建双馈风电机组频率响应模型如图4所示。为简化分析定义式（3）中常量ω1Lm=xad，图3～4中：ΔTm为双馈风机转子机械转矩扰动；ΔTe为电磁转矩扰动；Tj为双馈风机转子惯性时间常数；Δωr为转子转速扰动；ΔEq为内电势q轴分量扰动；Δθi为双馈风机内电势与静止坐标系x轴相位差扰动；Δθin为锁相环坐标下内电势相位与锁相环d轴相位差扰动；ΔθPLL为锁相环相位扰动；Δθs为双馈风机端电压相位扰动；kp、ki分别为锁相环控制比例、积分控制参数；kpω、kiω分别为转子侧变流器转速外环控制比例、积分控制参数；Δωrref为转子转速基准值扰动（一般为0）；Δird为转子侧d轴电流扰动；ωr为转子转速；Keq、Kθ均为中间变量；GPLL(s)为锁相环控制系统传递函数；ΔPm、ΔPe分别为机械、电磁功率扰动。

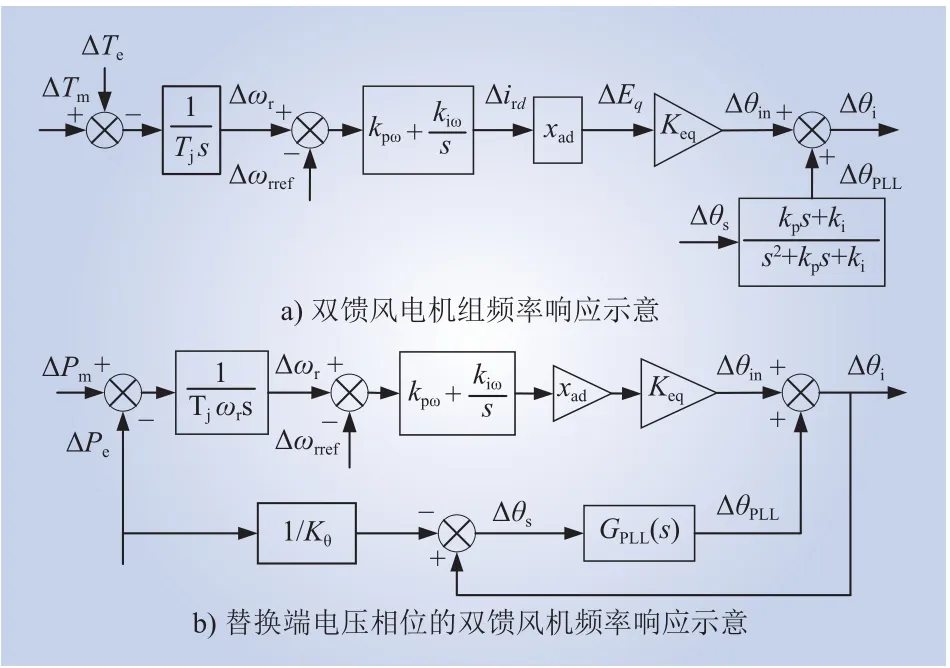
图4 双馈风电机组频率响应模型Fig.4 Frequency response model of DFIG

图4中

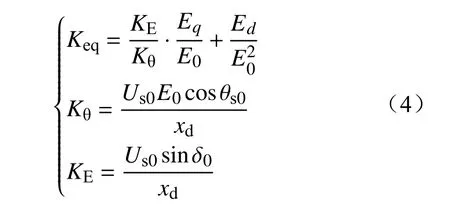
式中：Ed、Eq分别为内电势d、q轴分量；Us0为初始端电压、θs0为电压初始相位；δ0为内电势初始相位；xd为风机等效电抗；KE为中间变量。

为验证搭建模型有效性，在EMTDC/PSCAD搭建如图1所示双馈风机并网模型，在 Matlab/Simulink中搭建双馈风电机组频率响应模型，在相同的时间施加相同的扰动，观察二者输出量受扰动影响曲线的吻合度，具体参数取值如表1所示。

表1 双馈风电机组控制参数Table 1 Control parameters of DFIG

在50 s时给频率响应模型和时域仿真模型施加0.006 p.u.机械功率扰动，2个模型扰动响应曲线如图5所示，可以看出，在小扰动下，线性化和时域模型波形吻合度较高，本文建立的线性化模型能较好地反映系统的动态过程。

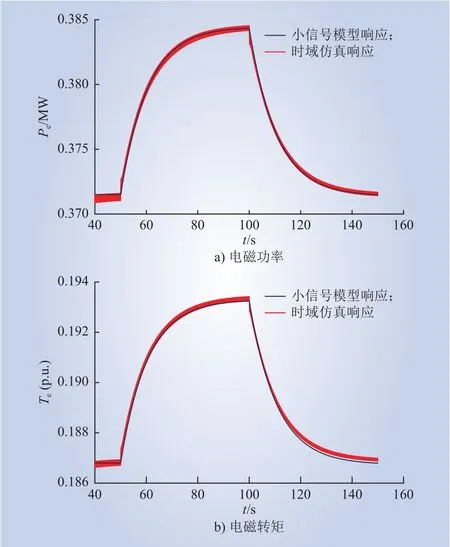
图5 单机频率响应模型和时域模型仿真结果对比Fig.5 Simulation result comparison between singlemachine frequency response model and time-domain model

2.2 双馈风电机组惯量特性

为使得双馈风电机组能够类比同步机内电势响应特性，评估双馈风机等效惯量，可将频率响应模型简化为如图6所示形式。图6中：Meq为等效惯量；D为中间变量；Δδ为内电势相位扰动。

图6 含等效惯量、阻尼的风电机组内电势相位动态响应Fig.6 Dynamic response of internal potential phase of wind turbine with equivalent inertia and damping

双馈风电机组等效惯量为

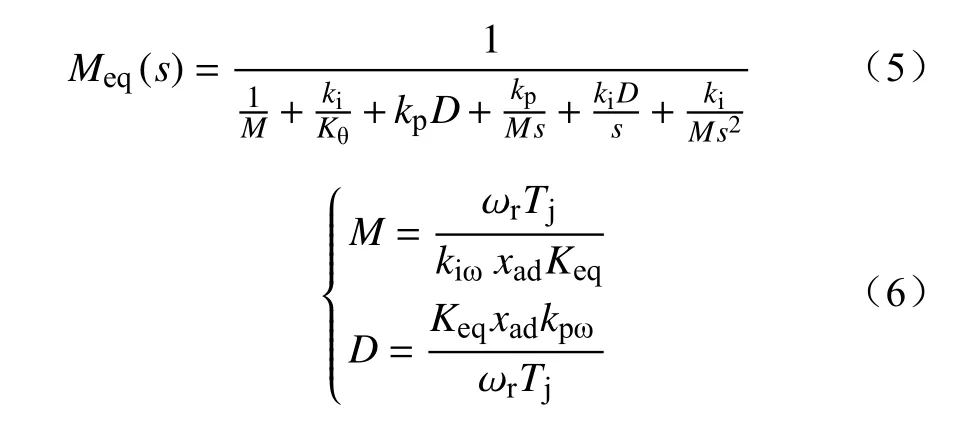
式中：M为中间变量。

基于式(5)所示双馈风电机组等效惯量表达式，可知双馈风电机组惯量由锁相环控制参数以及机组惯性时间常数等参数决定，得到不同锁相环控制参数下Meq(s)的幅频特性如图7所示。可以看出，在低频段，随着锁相环比例参数、积分参数的减小，锁相环响应速度减慢，双馈风电机组提供惯量增大。

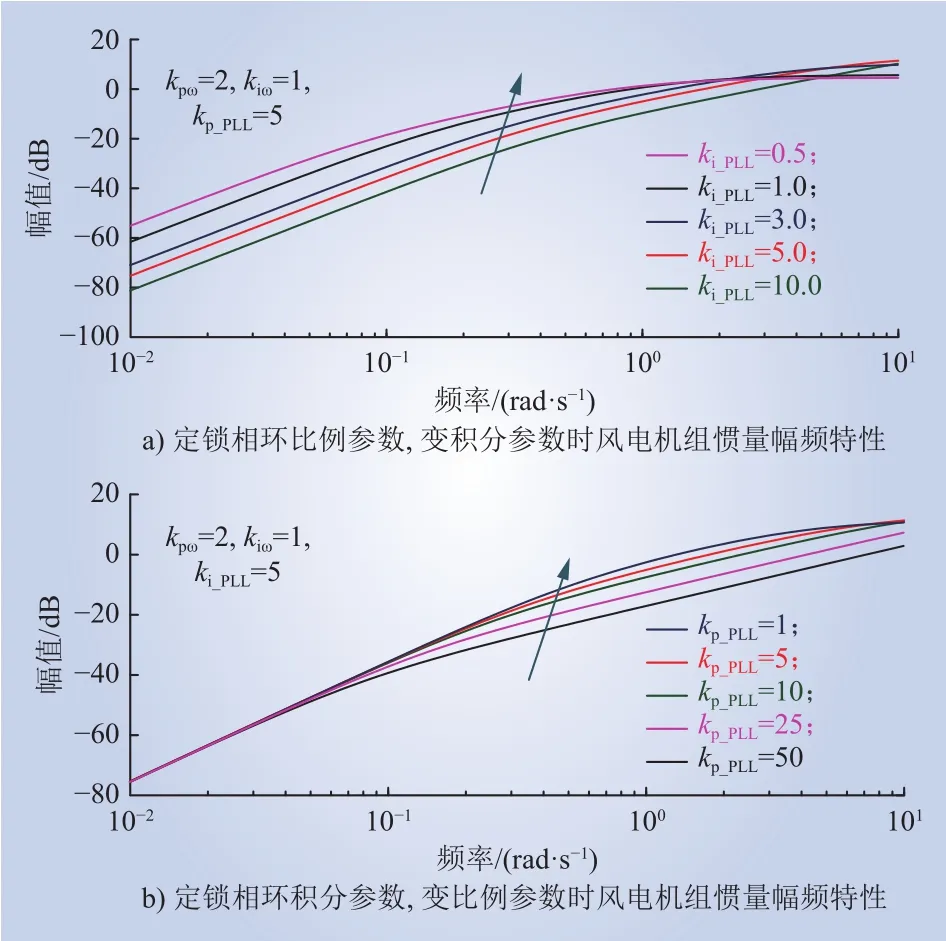
图7 双馈风电机组等效惯量Meq(s)幅频特性Fig.7 Amplitude-frequency characteristics of equivalent inertiaMeq(s) of DFIG

3 多风电机组并联参与频率调节动态协调机理

基于2.1节建立风电机组频率响应模型，建立2个双馈风力发电并网系统，其简化示意如图8所示，基于此分析系统发生频率扰动过程中各双馈风电机组之间不平衡功率分配机理[24]。

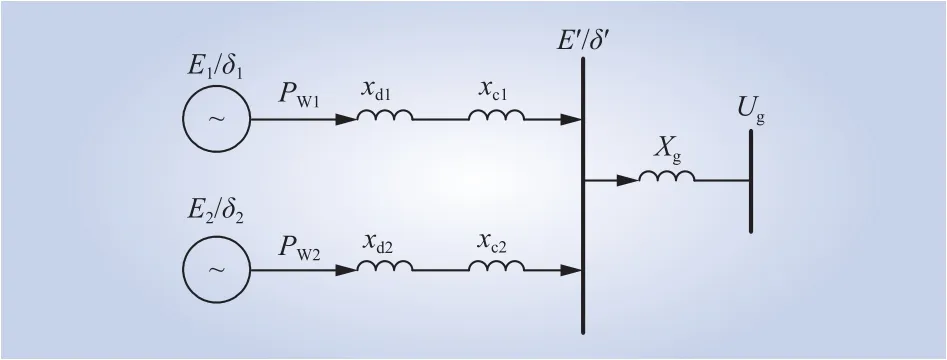
图8 两风力发电单元并联系统简化结构Fig.8 Simplified structure of parallel system of two DFIGs

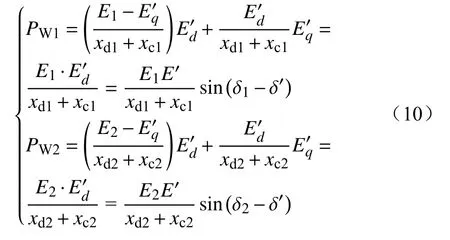
对式(10)进行线性化处理可得

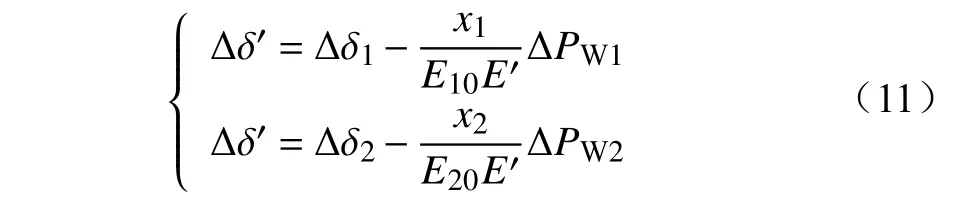
式中：E10、E20分别为2台双馈风电机组内电势电压初值；Δδ1、Δδ2分别为2台机组内电势相位扰动；Δδ'为并网点电压相位扰动；ΔPW1、ΔPW2分别2台机组的输出功率扰动；x1=xd1+xc1；x2=xd2+xc2。

基于图6所示单台双馈风电机组频率响应模型，结合式（11）可得到2台双馈风电机组并联系统频率响应模型如图9所示。

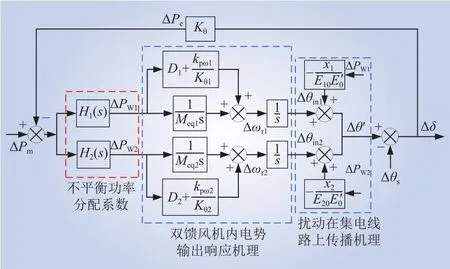
图9 两双馈风机并联系统频率响应模型Fig.9 Frequency response model of parallel system of two DFIGs

将时域仿真模型与频率响应模型对比验证，方法与上小节相同，2台机组参数取值均如表1所示，线性化和时域模型波形吻合度较高，本文建立的线性化模型能较好地反映系统的动态过程。

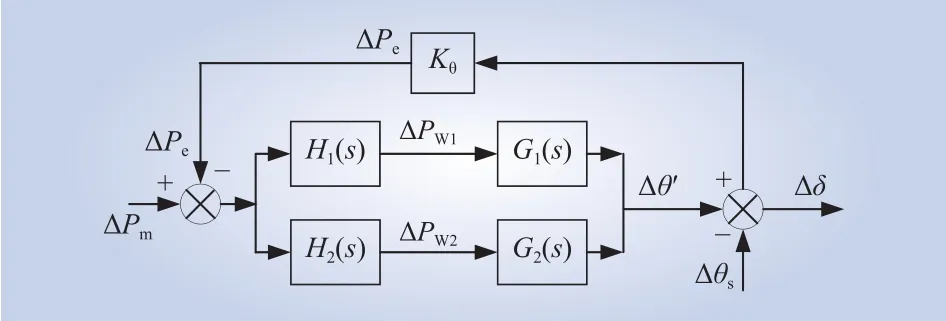
图10 两机系统频率响应简化模型Fig.10 Simplified frequency response model of twomachine system

将图9所示双风电机组并联频率响应模型简化为图10形式。求得并网点电势相位扰动为

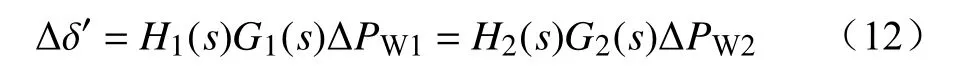
式中：H1(s)、H2(s)分别为2台风机的功率分配系数；G1(s)、G2(s)分别为2台风机输出功率和内电势相对PLLd轴相位扰动的传递函数。

整理可得不平衡功率分配系数为

由式(13)整理得到不平衡功率分配系数近似为

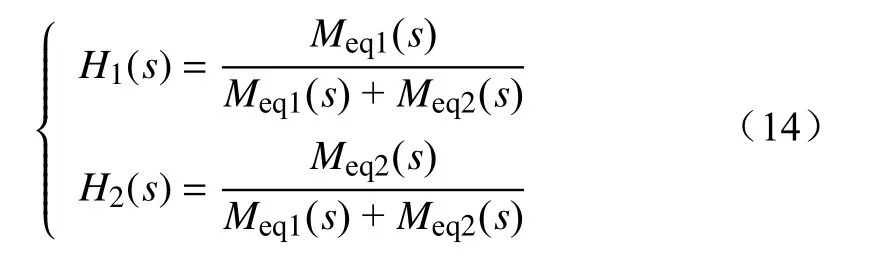
由式（14）可知，不平衡功率近似按照2台双馈风电机组惯量大小分配；可将此规律推广至多风电机组联网系统，假设系统中n台双馈风电机组并联，等效惯量分别为Meq1(s)，Meq2(s)，···，Meqn(s)，各机组不平衡功率分配系数如式（15）所示，即系统内不平衡功率近似按照各机组惯量大小分配。

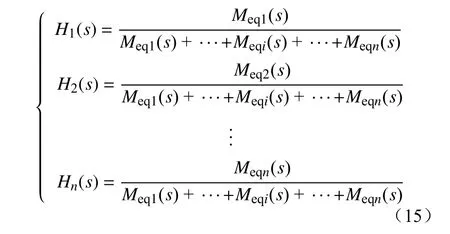
4 含风电联网系统频率响应分析

同步机频率响应模型（system frequency response, SFR）如图11所示[6]。结合双馈风电机组频率响应模型，分析双馈风机联网系统频率响应特性及风电联网对系统频率动态特性的影响。

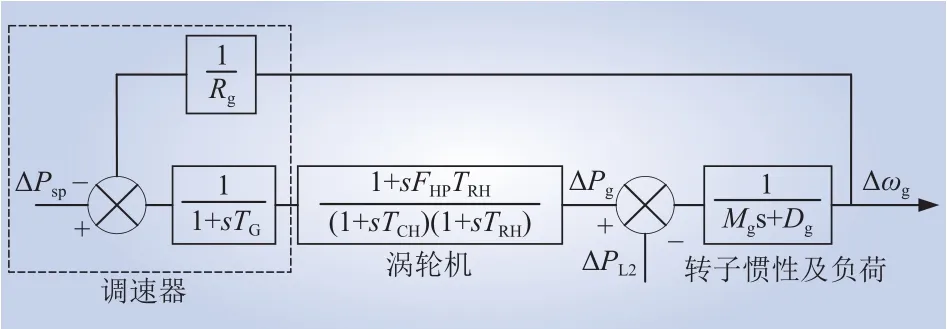
图11 再热式同步机组频率响应模型Fig.11 SFR model of reheat synchronous generators

由图11可知

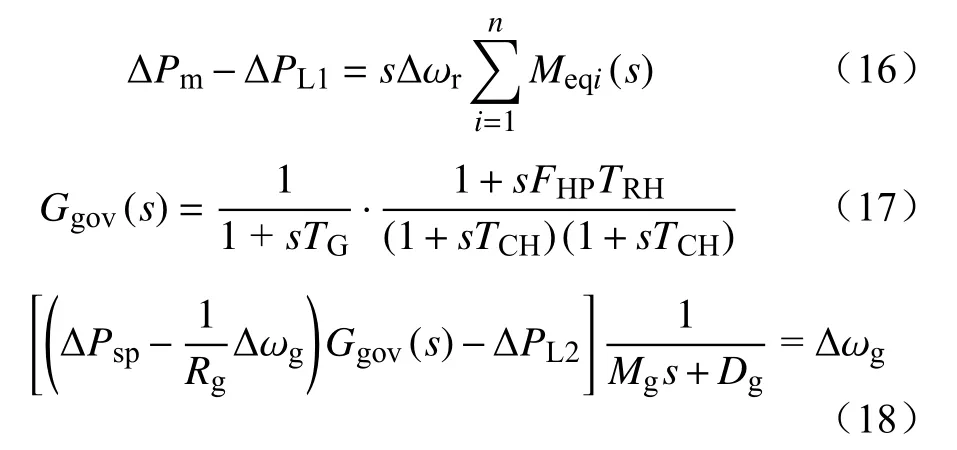
式中：n为风机台数；TG为同步机组惯性时间常数；ΔPL1、ΔPL2分别为风电机组和同步机组承担的功率；Dg为同步机组阻尼系数；Ggov(s)为同步机组原动机和调速器传递函数，其内部具体参数物理含义如表2所示；Δωg为同步机组转子转速扰动；ΔPsp为同步机组参考负荷（不计二次调频作用一般为0）。

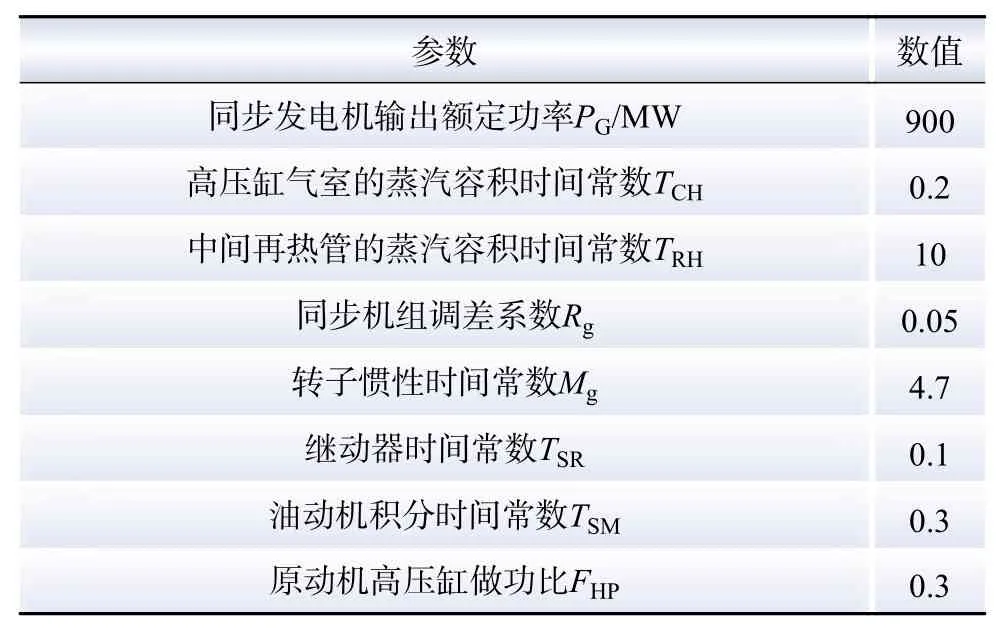
表2 同步机组参数Table 2 Parameters of synchronous generators

系统中不平衡功率ΔPL=ΔPL1+ΔPL2，并可认为 Δωr=Δωg时，结合式（18）有

当系统发生阶跃冲击负荷时，系统瞬时产生不平衡功率为ΔPL=ΔPs/s，ΔPs冲击负荷扰动幅值，得到

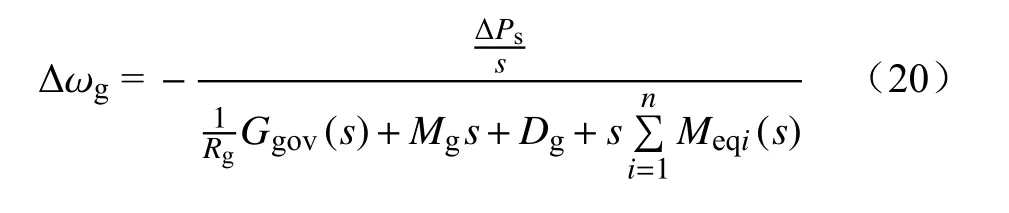
系统频率动态过程中有

如式（21）所示，在含双馈风电机组联网系统频率发生扰动初期，系统频率变化由系统内同步机组惯量及双馈风电机组惯量共同决定，同步机组提供惯量是不变的，因此风电机组提供惯量越大，系统频率变化率越小，系统频率稳定性越高；如式（22）所示，系统频率趋于稳定时，风电机组输出功率恢复至功率扰动前水平，频率特性仅由同步机组的调差系数、等效阻尼系数决定。

5 仿真及结果分析

在EMTDC/PSCAD中搭建如图12所示算例系统，包含3台容量为900 MW的同步机组和装机容量为450 MW的风电场，表1和表2分别为双馈风机和同步机组相关参数；系统负荷水平为1750 MW；本小节中风电场采用单机倍乘等值模型。

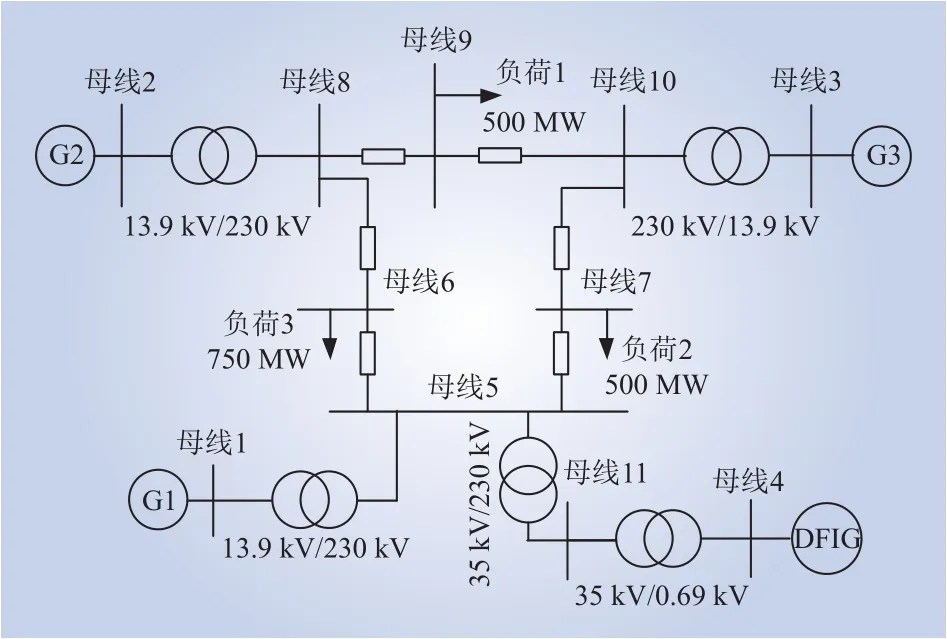
图12 算例系统结构Fig.12 Example system structure

5.1 不同锁相环参数下双馈风机惯量特性仿真分析

风电场中机组运行工况均为VW=8 m/s，系统负荷为 1750 MW，当t=40 s时，系统负荷增加200 MW，不同锁相环控制参数下系统频率响应、风电机组、风机转子转速和同步机输出功率响应情况如图13、14所示。

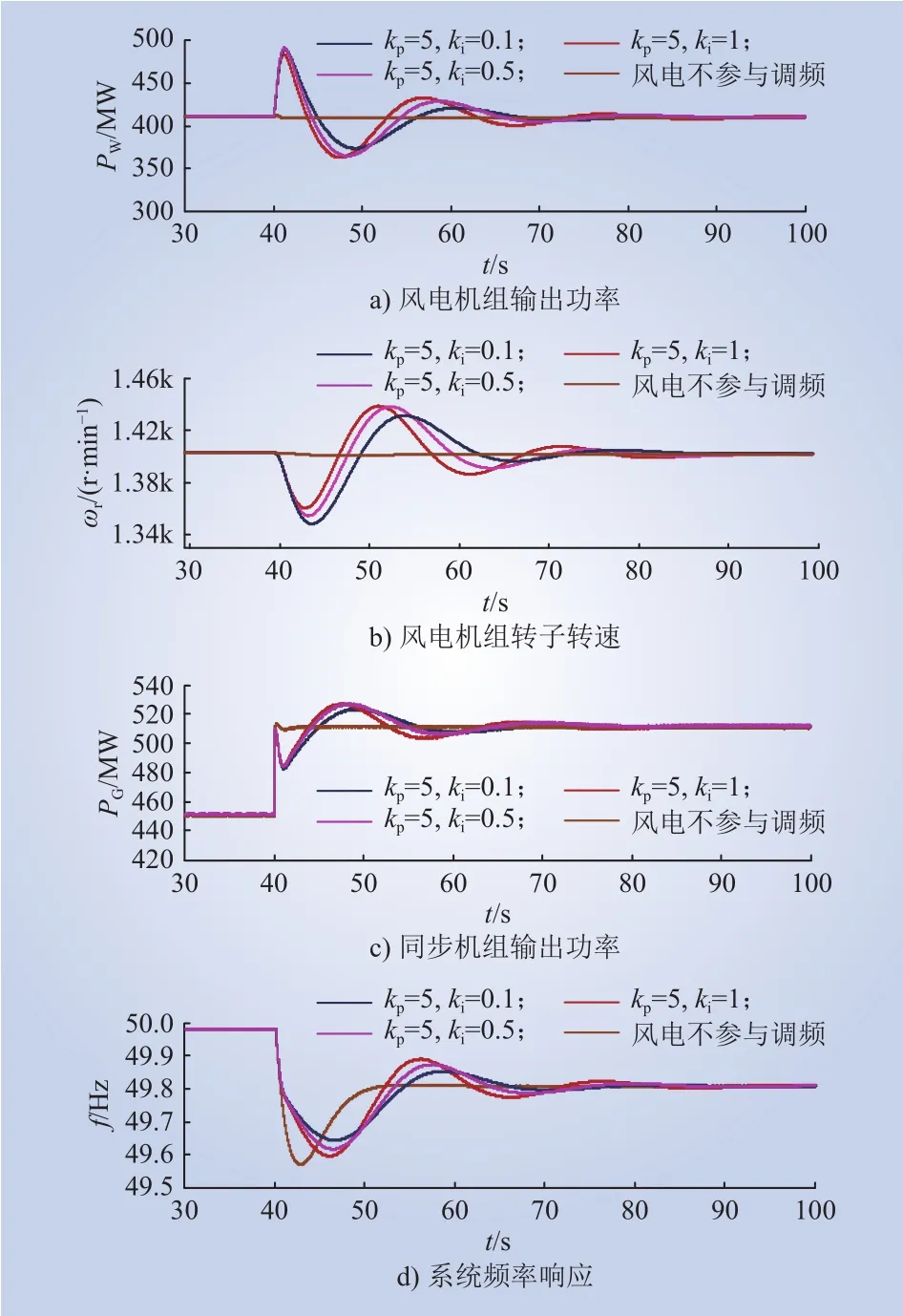
图13 不同锁相环积分参数下系统内各机组及频率响应Fig.13 Generator and frequency responses in the system under different PLL integral parameters

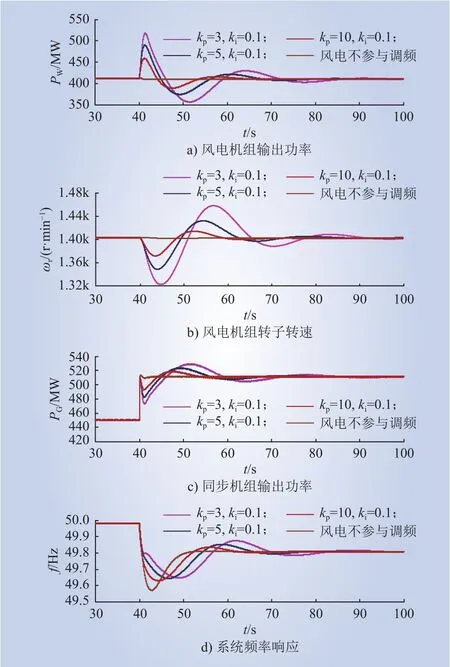
图14 不同锁相环比例参数下系统内各机组及频率响应Fig.14 Generator and frequency responses in the system under different PLL proportional parameters

如仿真结果所示，系统发生功率扰动，双馈风电机组不参与系统调频时，对系统表现出低惯量，系统频率变化率较大，频率最低跌落至49.6 Hz以下，严重危及系统频率安全稳定；优化双馈风电机组锁相环控制参数后，频率扰动初期，系统频率由同步机组惯性时间常数及双馈风电机组等效惯量共同决定，并随着积分参数逐渐减小(1→0.1)，以及比例参数逐渐减小(10→3)，锁相环响应速度减慢，双馈风电机组惯量增加，抑制系统频率变化，频率最低跌落程度降低，有利于提高系统频率稳定性。系统频率稳定后，双馈风电机组输出功率恢复到扰动前水平，系统频率仅取决于系统内同步机组调差系数与阻尼系数。

选取典型参数（kp=5，ki=1），将惯量响应过程中风电机组增发功率ΔPW与理论计算惯量响应功率Pinertia进行对比，如图15所示。

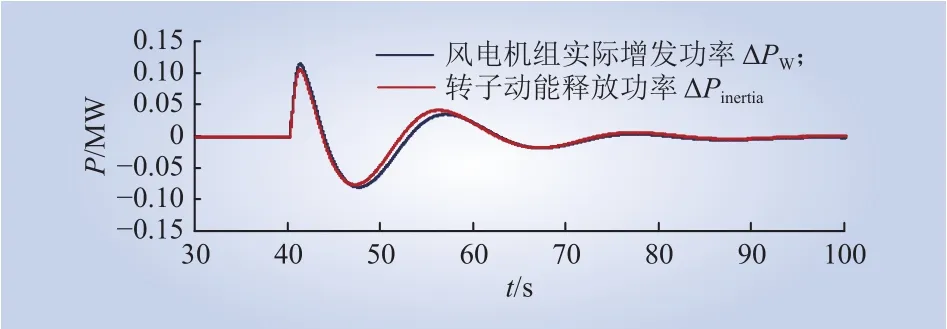
图15 转子动能释放功率和风电机组实际增发功率Fig.15 Kinetic energy releasing power of rotor and actual additional power of DFIG

由图15可知，系统受频率扰动后系统内风电机组实际增发功率数值上等于由转子转速变化释放的功率，惯量响应过程中风机增发功率能量来源于转子。

5.2 不同控制参数下多风电并联仿真分析

本算例下风机运行工况与系统负荷水平与5.1小节相同，将风电场内机组分成运行工况不同的机群，分别用风电机群1、风电机群2表示，2个机群的动态特性表征风电场的动态特性。分别使风电机群1和2在系统频率动态过程中保持锁相环积分参数不变(ki=0.1)，机群1内风电机组比例参数kp1=3，机群2风电机组比例参数kp2=10；当系统发生200 MW冲击负荷时频率响应及风电出力如图16所示。

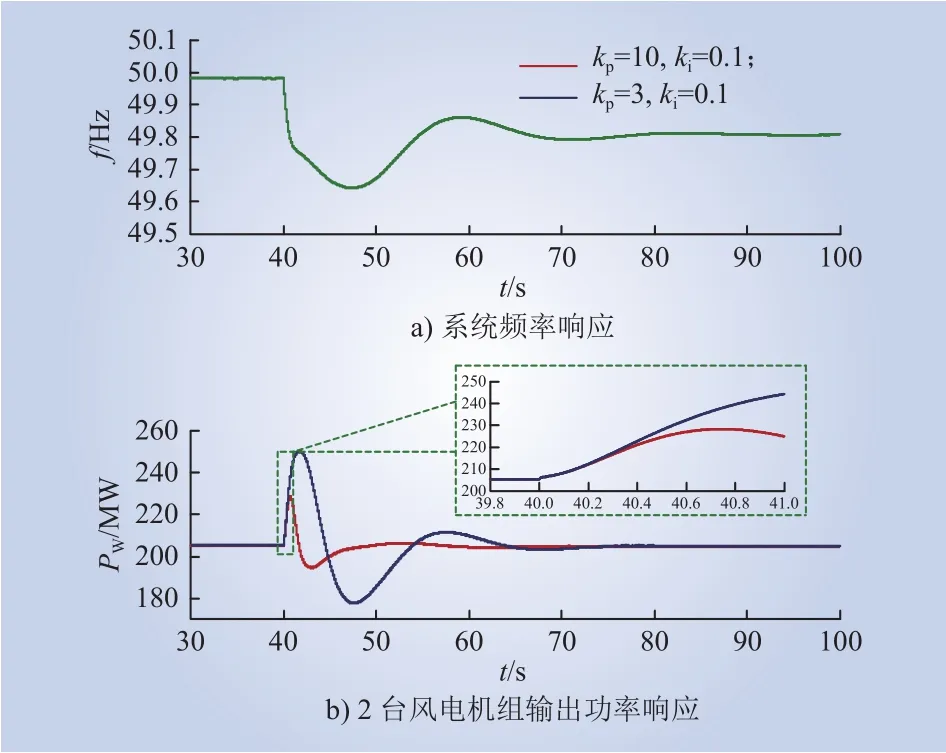
图16 不同锁相环比例参数下两风机及系统频率响应Fig.16 DFIG and frequency responses under different PLL proportional parameters

保持锁相环比例参数不变(kp=5)，机群1风电机组锁相环积分参数ki1=0.1，机群2风电机组锁相环积分参数ki2=10；系统发生200 MW冲击负荷扰动时系统频率响应及风电出力情况如图17所示。

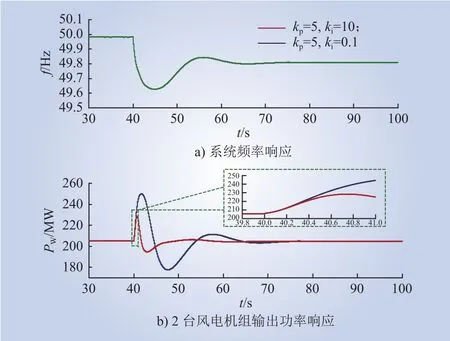
图17 不同锁相环积分参数下两风机及系统频率响应Fig.17 DFIG and frequency responses under different PLL integral parameters

如仿真结果所示，系统发生频率扰动后，控制机群1锁相环积分参数ki1小于机群2积分参数ki2，或机群1锁相环比例参数kp1小于机群2比例参数kp2，机群1的惯量G1(s)大于机群2的惯量G2(s)，不平衡功率分配系数M1(s)大于风电场2的不平衡功率分配系数M2(s)，因此机群1在系统频率动态过程中承担不平衡功率大于机群2承担的不平衡功率，在功率扰动过程中发挥了更大的作用。

6 结论

本文建立了双馈风电机组频率响应模型，分析了锁相环控制参数对其惯量特性影响；建立了2台双馈风电机组并联的频率响应模型，分析了多风电并联系统中不平衡功率分配机理，推导了不平衡功率在各个风电机组间分配系数；建立含双馈风电机组联网系统频率响应模型，并分析功率扰动各阶段频率主要影响因素，主要结论如下。

双馈风电机惯量特性与锁相环控制参数、转速环控制参数及双馈感应电机转子惯性有关，其惯量随着锁相环比例，积分参数减小而增大，在系统发生功率扰动初期优化锁相环控制参数，能增大双馈风电机组惯量，有效抑制系统频率变化，无须附加控制即能提高系统频率抗干扰能力。在多机联网系统中，各双馈风电机组承担的不平衡功率近似按照其惯量大小分配，惯量越大的机组承担更多的不平衡功率，对系统频率稳定性的贡献也越大。