基于MATLAB的S环形无碳小车的凸轮设计研究

彭潇潇 欧友良 邹 权 仇朝阳

（1.湖南工程学院，湘潭 411101；2.国网湘潭供电公司，湘潭 411104）

小车设计源于第七届全国大学生工程训练竞赛命题。比赛规定，由学生设计并且制备一台可以自主控制方向的势能驱动车，小车在行驶的过程中与地面接触，且所需要的驱动能量全部由重力势能转换而 来[1-2]。小车要求在赛道内连续稳定穿过障碍桩，走出S环形轨迹[3]，如图1所示。

依据上述要求，设计提出了一种凸轮控制转向的三轮结构小车。三轮分别为主动轮、前轮和从动轮，如图2所示。凸轮可以控制前轮的转向角度，所以凸轮设计是小车的核心技术问题。

1 S环形小车及凸轮设计

采用MATLAB参数优化分析设计的方法仿真得到凸轮形状。需要事先确定小车前轴到后轮轴的距离A和主动轮偏距eL，如图3所示。

本文创新性地提出了设计前轮转角来推出凸轮推程的方法。由于S环形轨迹是中心对称，所以只需要设计半个S环形的轨迹就可以设计出凸轮。首先，按角度等分，将凸轮分成N份，设置凸轮每转过360°/N时主动轮走过的距离为LT（仿真中取0.00006）。小车起始点为O，坐标为（-1.8，0），主动轮垂直于水平线。设置主动轮偏距eL、节点距离LT、前轮转角θ、主动轮与各桩连线（对称轴）的夹角ϕ、前后轴距离A等参数，则可以推算出小车各个点的行走轨迹。设phi为主动轮转过的角度，x为O点横坐标，y为O点纵坐标，l为凸轮每转过360°/N时O点经过的距离，lz为下一步左轮前进距离，ly为下一步右轮前进距离，lq为下一步前轮前进距离，xz为从动轮横坐标，yz为从动轮纵坐标，xy为主动轮横坐标，yy为主动轮纵坐标，xq前轮横坐标，yq为前轮纵坐标。

计算的相关代码如下：

拟定轨迹如图4所示，凸轮每转过一圈，小车需走出一个S环形，前轮转向需经历“左转—右转—左转—右转—左转—右转—左转—右转—左转”的过程。在设计小车的前轮转角曲线时，为了保证前轮转角曲线的曲率连续，小车左转到右转的过渡用正弦曲线实现，且设置小车右转和左转时的前轮转角为一常数（即小车走圆弧轨迹）。

要实现的目标：（1）设置起点坐标为（-1.8，0），起始方向如图4所示；（2）调试出如图4所示轨迹，使轨迹完全闭合；（3）行走过程后轴中点O与各障碍物（包括极限位置）的距离尽可能保持一致，减小发生撞桩的可能性。

为调出满足上述要求的曲线，需要设置前轮转角曲线的几个参数：主正弦曲线的幅值a、b、c、d、e，决定了小车左转右转的幅度大小；各段曲线节点数N1、N2、N3、N4、N5、N6、N7、N9、N10，决 定 小车左转和右转时走过的距离；节点数之和与LT的乘积，即小车走过一个周期的距离。

通过调节以上几个参数，可以得到当设置参数如下时，小车的轨迹最为理想：N=187206、N1=15000、N2=3000、N3=16500、N4=3000、N5=16500、N6=0、N7=18000、N8=3000、N9=17000、N10=[N-2(N1+N2+N3+N4+N5+N6+N7+N8+N9)]/2。

前轮转角各段曲线幅值a=0.165、b=-0.275、c=0.24、d=-0.190495815、e=0.278299408。

前轮转角确定后，通过设置凸轮偏距、基圆半径R0以及与凸轮接触的轴的直径da，即可推算出凸轮的推程，进而得到理论凸轮的形状，如图5所示。

自行设置好传动i后，可推得后轮直径，此时得到的直径为非整数。为了得到较为简洁直观的数据，可以微调节点数，微调后可获得前轮传动比i为27.5时，后轮直径为130.00 mm，传动比较大，故选择二级传动。取i1=5，i2=5.5，齿轮模数取1，齿数取z1=z2=20、z3=100、z4=110。

理论凸轮无法直接应用到无碳小车上，除了凸轮推程最大的点，接触轴与凸轮的理论接触点和实际接触点均不在同一位置。为解决这个问题，用椭圆对理论凸轮进行包络，求得其内包络线即为所需的实际凸轮[4-5]，如图6所示。

2 小车各参数

经MATLAB仿真或自行设计得到的小车参数，如表1所示。

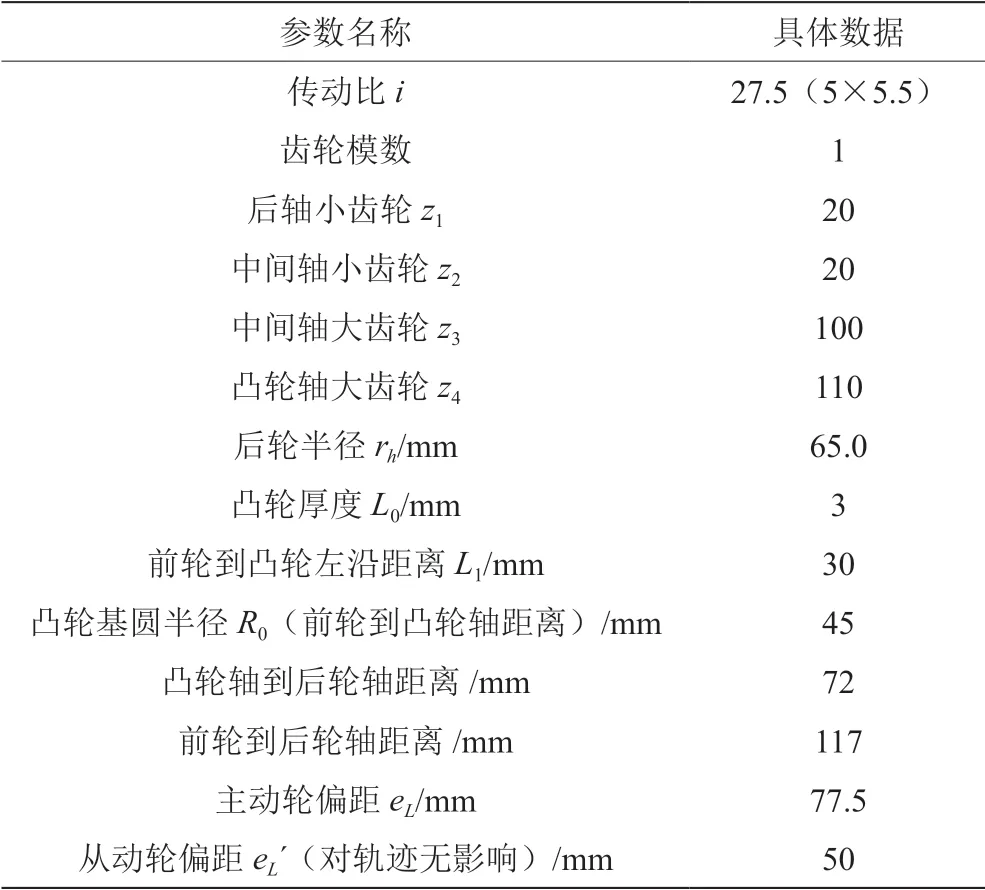
表1 小车参数

3 轨迹仿真

将路程分成N份，从初始点开始，一步一步迭代求出下一节点的坐标，进而仿真轨迹。仿真目标为后轴中心、主动轮、从动轮和前轮的轨迹。

首先，确定小车参数。参数主要有主动轮与前轮的偏距eL、前后轴距离A、小车行走过程的曲率p、凸轮旋转一圈时的主动轮路程L。设置小车的车身倾角为φ，前轮转角为θ，则前轮转角θ=arctanpA。

将路程分为N份后，每两节点间主动轮前进的距离ly、每两节点间后轴中心前进的距离l、从动轮前进的距离lz以及前轮前进的距离lq分别为：

其次，在确定节点间距离后，可开始轨迹仿真，以后起始点以O为例。设小车后轴中心的初始点O为（-1.8，0），主动轮、从动轮和前轮的初始坐标可以根据小车结构参数求得。此时，小车车身水平向下（ϕ=90°），采用迭代进行轨迹求解的方法，有车身倾角ϕ(i+1)、后轴中心横坐标x(i+1)和后轴中心纵坐标y(i+1)分别为：

对上述步骤循环N次，即可求得凸轮旋转一圈，即小车走出半个S环形时的后轴中心轨迹。主动轮和从动轮的轨迹求解与后轴中心类似，只需将l替换城ly或lz即可。对于前轮的行走轨迹，还应考虑前轮转角的影响，仿真时需在车身倾角ϕ后加上前轮转角θ后再进行轨迹求解。

前轮、主动轮、从动轮的轨迹仿真如图7所示。

4 结语

本文提出利用MATLAB参数优化方法设计S环形无碳小车的凸轮结构，对小车结构创新和优化具有重要指导意义。利用本设计思路进一步进行三维运动仿真，可为小车后期设计制作实物提供便利，节省了大量的人力、物力和财力。试验结果表明，设计的S形无碳小车能有效优化运动轨迹。