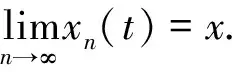一类三阶微分方程特殊正解的存在性
2022-07-23赵玉萍
赵玉萍,傅 华
(1.青海民族大学数学与统计学院,青海 西宁 810007;2.福建警察学院计算机与信息安全管理系,福建 福州 350007)
0 引言
微分方程在计算机科学、经济学、生物数学等领域有着广泛应用,微分方程的渐近性和正解存在性问题越来越受到人们的重视.关于二阶微分方程的渐近性和正解存在性问题的研究成果较多[1-8],对高阶和分数阶微分方程解的振动性、渐近性的研究引起了国内外学者的广泛关注[9-16],但是对高阶微分方程正解的存在性问题研究较少.文献[9]只研究了三阶非线性微分方程
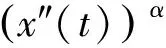
解振动的充分条件,并没有考虑解的存在性和渐近性问题.文献[11]研究了一类三阶拟线性微分方程
(a(t)|x′(t)|α-1x′(t))′′+b(t)|x(t)|β-1x(t)=0
正解的存在性.
受前述工作启发,本文研究三阶非线性微分方程
(a(t)|x′(t)|α-1x′(t))′′+b(t)f(x(t))=0,0 (1) (2) 引理1 设条件(2)成立,x(t)是方程(1)的正解,则x(t)只有下面两种可能,即存在T≥t0,使得当t≥T时,有: x(t)>0,x′(t)>0,(a(t)|x′(t)|α-1x′(t))′>0; (3) x(t)>0,x′(t)<0,(a(t)|x′(t)|α-1x′(t))′>0. (4) 证明这个引理的证明过程与文献[6]引理1与引理2证明类似,此处省略. 当条件(2)成立时,如果x(t)是方程(1)的正解,由引理得 (a(t)|x′(t)|α-1x′(t))′>0, 则存在T,当t>T时, a(t)|x′(t)|α-1x′(t)≥a(T)|x′(T)|α-1x′(T)=c>0. 将上式两边从T到t积分,得 则存在k1>0,使得 那么当(2)式成立时,如果x(t)满足条件(3)且 (5) 则称x(t)是方程(1)满足条件(3)的正解中的最小解. 当条件(2)成立时,如果x(t)是方程(1)的正解,由方程(1)得 (a(t)|x′(t)|α-1x′(t))″=-b(t)f(x(t))<0. 因此 (a(t)|x′(t)|α-1x′(t))′≤(a(T)|x′(T)|α-1x′(T))′=b>0,t≥T. 将上式两边从T到t积分两次,得 其中b1=a(T)|x′(T)|α-1x′(T).则存在k2>0使得 那么当(2)式成立时,如果x(t)满足条件(3)且 (6) 则称x(t)是方程(1)满足条件(3)的正解中的最大解. 本文主要讨论在满足条件(3)的情形下,方程(1)正解中最小解与最大解存在的充分和必要条件. 定理1 设条件(2)成立,x(t)是方程(1)满足条件(3)的正解中的最小解,则 (7) 证明设x(t)是方程(1)满足条件(3)的正解中的最小解,则存在T≥t0,使得 (8) 当t>T时,必有 a(t)|x′(t)|α-1x′(t)<(3k)α. 若不然,则 x′(t)≥3k(1/a(t))1/α. 将上式从T到t积分,得 这与(8)式矛盾.说明0 将方程(1)从t到T积分,令T→∞得 将上式从t到τ积分有 而a(t)|x′(t)|α-1x′(t)有界,所以 由已知有 再由(8)式得 因此 从而(7)式得证. 定理2 设条件(2)成立,且 (9) 则方程(1)存在满足条件(3)的正解中的最小解. 证明假设(9)式成立,令T≥t0,存在常数ρ>0,使得 (10) 假设x(t)是方程(1)的正解中的最小解,则 令I=[T,∞),C[T,∞)是X:I→R上所有连续函数构成的空间,并且所有连续函数具有一致收敛于[T,∞)的紧致子区间的拓扑性质.定义C[T,∞)上子集合X满足 集合X是定义在C[T,∞)上的闭凸子集,定义映射ψ:X→C[T,∞),满足 应用Schauder-Tychonoff不动点定理证明ψ有不动点x(t),使得 x(t)=(ψx)(t),t≥T. (1)ψ是X到X上的映射.令x∈X, 由已知得 记ρ=f(x(T)),由(10)式有 从而ψx∈X. |(ψxn)(t)-(ψx)(t)|≤ 其中 进而有|(ψxn)(t)-(ψx)(t)|→0 (n→∞)在[T,T*]⊂I上一致成立,则ψ是X上的连续映射. (3)ψx是相对紧的.令T*>T相对固定,则有 所以ψx在[T,T*]上一致有界,进而ψx在I上等度连续,由Ascoli-Arzela定理,得ψx是C[T,∞)相对紧子集. 因此,对映射ψ:X→C[T,∞),应用Schauder-Tychonoff不动点定理,存在不动点x(t)∈X,当t≥T时,x(t)=(ψx)(t),且x(t)∈X是方程(1)满足条件(3)的正解中的最小解. 定理3 设条件(2)成立,x(t)是方程(1)满足条件(3)的正解中的最大解,则 (11) 证明设x(t)是方程(1)满足条件(3)的正解中的最大解,则存在T≥t0,使得 将(1)式从t到τ积分,由引理1得 而(a(t)|x′(t)|α-1x′(t))′有界,则有 从而(11)式得证.定理3证毕. 定理4 设条件(2)成立,且 (12) 则方程(1)存在满足条件(3)的正解中的最大解. 证明假设(12)式成立,令T≥t0,存在常数ρ>0,使得 记 令A=[T,∞),C[T,∞)是X:A→上所有连续函数所构成的空间,并且所有连续函数具有一致收敛[T,∞)的紧致子区间的拓扑性质,定义C[T,∞)上子集合X满足 X={x∈C[T,∞)|kW(t,T)≤x(t)≤2kW(t,T)}. 集合X是定义在C[T,∞)上的闭凸子集,定义映射φ:X→C[T,∞),满足: 类似定理2的证明,可以验证: (1)φ是X到X上的映射; (2)φ是X上的连续映射; (3)φx是相对紧的. 因此,对映射φ:X→C[T,∞),应用Schauder-Tychonoff不动点定理,存在x(t)∈X,当t≥T时,x(t)=(φx)(t),且x(t)∈X是方程(1)满足条件(3)的正解中的最大解.证毕. 特别地,若方程(1)中的常数α和函数f(u)的性质稍做改动,则有下面的结论: (13) 对上式从t到∞积分,有 对上式从t2到∞积分,有 后续工作中,可以进一步讨论当条件(4)成立时,方程(1)正解中最小解与最大解存在的充分和必要条件.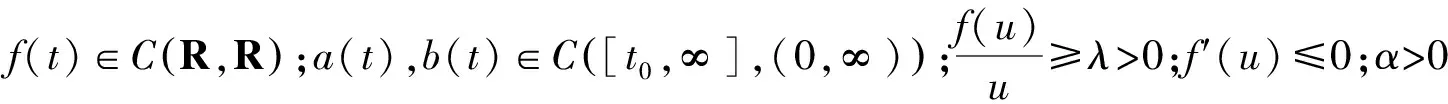
1 基本引理


2 主要结果