非线性时间分数阶色散方程的分支问题与精确解研究
2022-07-23芮伟国
张 慧,芮伟国
(1.绵阳城市学院通识教育学院,四川 绵阳 621000;2.重庆师范大学数学科学学院,重庆 401331)
分数阶导数的概念最早出现在1695年L’Hospital和Leibniz的往来书信中.此后,经过几百年的发展,分数阶微积分理论逐渐建立起来.与整数阶微积分模型相比,越来越多的研究者发现分数阶微分模型可以更准确地描述数学力学、控制理论、信号处理等各个领域的复杂问题.尤其在过去的几十年间,分数阶微积分被公认为是描述长记忆过程、黏弹性现象和反常扩散行为的最佳工具之一.
近几十年来,出现了许多求解非线性分数阶微分方程的有效方法.主要有Adomian分解法[1-2]、第一积分法[3]、同伦分析法[4-5]、李群论方法[6]、不变子空间法[7-8]、分数变分迭代法[9]、分数复变换法[10-11]、分离变量法[12-13]、分离变量法结合齐次平衡原理或积分分岔方法[14-15].这些方法对于求解更复杂的分数阶非线性偏微分方程来说是远远不够的.因此,寻找求解分数阶非线性偏微分方程的新方法和新的分析工具成为当前和未来的首要任务.
本文利用文献[16]关于分离变量法与动力系统方法相结合的思想,研究三阶非线性时间分数阶色散方程解的存在性、精确解和解的动力学性质.
1 三阶非线性时间分数阶色散方程Kα(0,2,0)
研究下列时间分数阶色散方程[17],记为Kα(m,n,p):
(1)
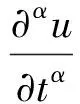
考虑三阶时间分数阶非线性方程Kα(0,2,0):
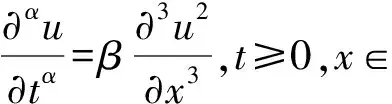
(2)
其中u=u(x,t),α∈(0,1).当α=1时,文献[18]深入研究了三阶非线性色散方程的激波和爆破问题.文献[19-20]首次在非线性色散方程Compacton解的观点下研究了其一般情形.
方程(2)可化简为

(3)
假设方程有如下形式的解:
u=[a0+a1v(x)]tγ.
(4)
其中:v=v(x)为待定函数;a0,a1,γ为待定常数.将(4)式代入(3)式得
(5)
利用齐次平衡原理,令γ-α=2γ,可得γ=-α.将γ=-α代入(5)式中,等式两边同时除以t-2α得
(6)
将(6)式对x积分一次,并令积分常数为零,则
(7)

(8)
当v=-a0/a1时,dy/dx无定义,由此称v=-a0/a1为系统(8)的奇异线.显然,当v=-a0/a1时,系统(8)与方程(7)不等价.为了使二者完全等价,只需做变换
dx=2βa1(a0+a1v)dτ,
(9)
其中τ为参数,则系统(8)可化简为一个正则系统:
(10)
系统(10)与系统(8)具有相同的首次积分
(11)
其中h是积分常数.为了方便下面的讨论,将(11)式改写为
(12)
2 系统相图分支
对系统(10)平衡点的性质及可能出现的相图进行分析.除奇异直线v=-a0/a1外,系统(8)与系统(10)是拓扑等价的.因此,奇异系统(8)的相图是由奇异直线v=-a0/a1周围的拓扑结构和正则系统(10)的相图构成.

设M(v,y),J(v,y)分别为系统(10)的雅克比矩阵和行列式,则有:
(13)
(14)
将平衡点代入(12),(14)式中可得
(15)
(16)
根据平面动力系统的分岔理论[21-25],有下面2个引理:
引理1 对于平面可积系统的平衡点有以下结论:(1) 当J(vi,yi)<0,系统的平衡点为鞍点;(2) 当J(vi,yi)>0且TraceM(vi,yi)=0,系统平衡点为中心;(3) 当J(vi,yi)>0且[TraceM(vi,yi)]2-4J(vi,yi)>0,系统平衡点为结点;(4) 当J(vi,yi)=0且Poincaré指数为0,系统平衡点为尖点,否则为高阶奇点.
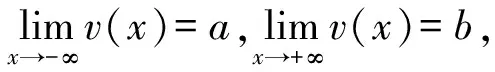
(1) 当a=b时,系统(8)具有同宿轨道,因此方程(7)具有孤立波形式的同宿解;
(2) 如果a≠b时,系统(8)有一条异宿轨道,因此方程(7)具有一个扭结或反扭结波形的异宿解;
(3) 若系统(8)有一条围绕中心点的闭合轨道,则方程(7)具有周期解;
(4) 如果系统(8)具有等腰三角形的异宿轨道,且等腰三角形的底部是一条奇异线,则方程(7)具有尖波解.
由引理1易知:A点为尖点;C1,2点为鞍点;当βa1Ω>0时,B1,2点为鞍心,当βa1Ω<0时,B1,2点为中心.利用引理2可知,(7)式的孤立解对应于系统(8)的同宿轨道,方程(7)的异宿解对应于系统(8)的异宿轨道,方程(7)的周期解对应于系统(8)的闭轨道.
根据以上信息,在不同的参数条件下,绘制系统(8)的相图分支,如图1—2所示.需要注意的是,图中的所有轨道曲线在平衡点外并不相交,一条轨道对应于方程(7)的一个解.
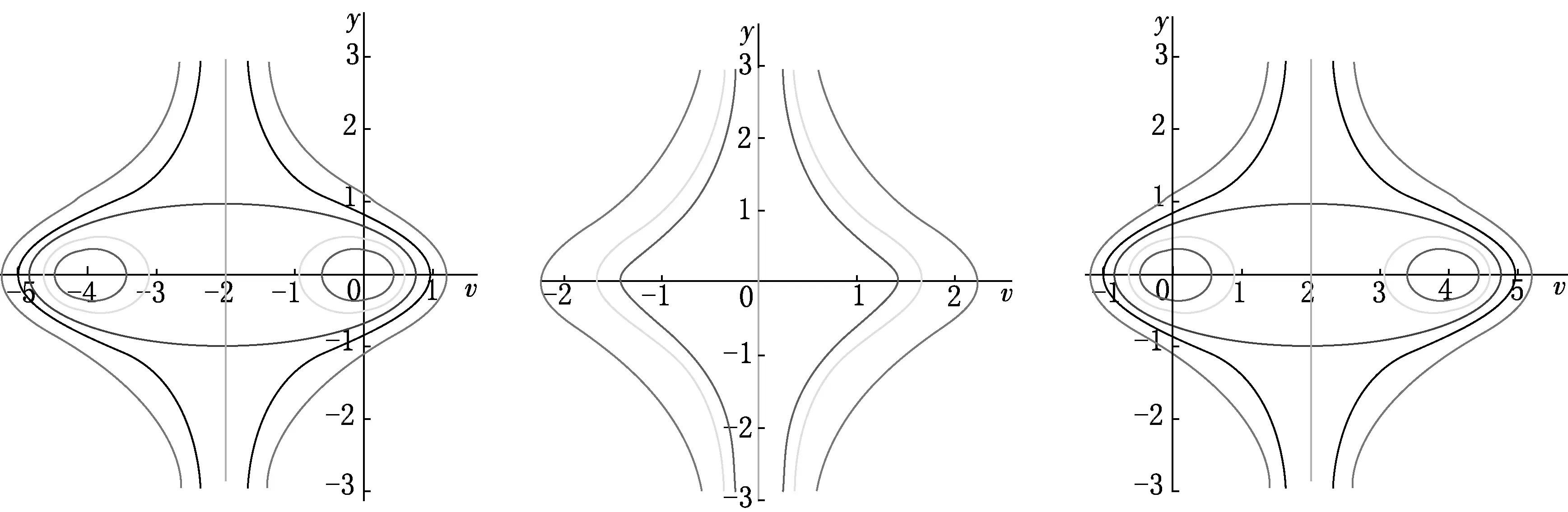
(a) a0>0 (b) a0=0 (c) a0<0
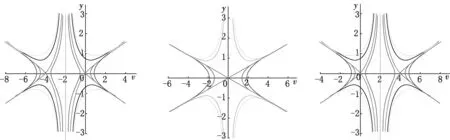
(a) a0>0 (b) a0=0 (c) a0<0
3 色散方程Kα(0,2,0)的精确解
系统(8)在不同参数下的相图分支中的每一条轨道对应于方程(7)的一个解.
3.1 在h=h1,βa1Ω<0,a0≠0条件下色散方程Kα(0,2,0)的精确解
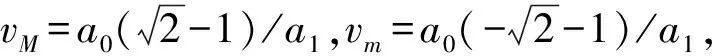
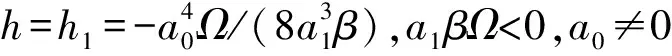
(17)
将(17)式代入系统(8)的第一个方程中,并沿通过点(vM,0)的闭轨道积分得
(18)
求解(18)式,可得(7)式的一个光滑周期解
(19)
(20)

图3 解(20)随时间和空间变量演化的三维图
由于当t→+∞时,u→0,故解(20)是具有周期性和衰减性的稳定解.为了直观地显示解(20)的动力学性质,取a0=a1=1,β=-2,α=0.75,绘制解(20)的动力学曲线图,如图3所示.
3.2 在h20条件下色散方程Kα(0,2,0)的精确解
当h2
在以上的条件下,方程(11)可化简为
(21)

(22)
这里v1>v3>v4>v2.故(21)式可改写为
(23)
以(v3,0)为初始条件,将(23)式代入(10)式的第一个方程,并积分可得
(24)
由此可得
(25)
其中
将(25)式代入变换(9)进行积分,可得
(26)
将(25)式代入(4)式,结合(26)式可获得方程(3)的精确解:
(27)

类似地,解(27)满足当t→+∞时,u→0.故解(27)定义了一类具有周期性和衰减性的稳定解族,其动力学性质和剖面与解(20)非常相似.
3.3 在h>h1,β a1Ω<0,a0a1>0条件下色散方程Kα(0,2,0)的精确解
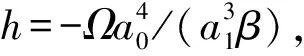
(28)
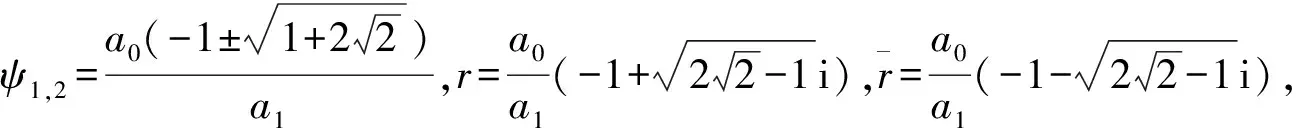
(29)
求解上式可得
(30)
其中:
将(30)式代入dx=2βa1(a0+a1v)dτ中,再积分,同样令积分常数为0,可得
(31)
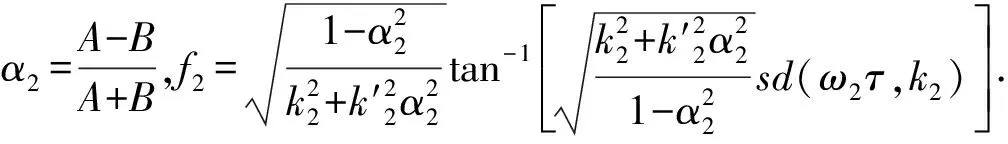
将(30)式代入(4)式,结合(31)式可获得方程(3)的如下精确解:
(32)

图4 解(32)随时间和空间变量演化的三维图
当t→+∞时,u→0,故解(32)是一个具有Compaction性的渐进稳定解.为了直观地显示解(32)的动力学性质,取a0=a1=1,β=-2,α=0.35,绘制解(32)的动力学曲线图,如图4所示.
3.4 在h=h2,β a1Ω>0,a0>0条件下色散方程Kα(0,2,0)的精确解
当h=h2=0,βa1Ω>0,a0>0时,系统(8)总是有4条光滑的异宿轨道(见图2)穿过鞍点B1(0,0),B2(-2a0/a1,0).将上述条件代入(11)式,再将其代入(10)式中的第一个方程可得
(33)

(34)
将(34)式代入dx=2βa1(a0+a1v)dτ中,再积分,同样令积分常数为0,可得
(35)
将(34)式代入(4)式,再结合(35)式可获得方程(3)的6个精确解:
(36)
(37)
(38)
(39)
(40)
(41)
其中:τ为参数,Ω=Γ(1-α)/Γ(1-2α),α≠1/2.
为了能够直观地展示上述解的动力学行为,绘制一些具有代表性解的3维坐标演化图形.取a0=a1=1,β=2,α=0.35,ε=1,绘制出解(36)的坐标演化图形,如图5(a)所示;取a0=a1=1,β=2,α=0.35,ε=-1,绘制出解(38)的坐标演化图形,如图5(b)所示.

(a)解(36)的3维图 (b)解(38)的3维图图5 解(36),(38)随时间和空间变量演化的3维图
3.5 在h10条件下色散方程Kα(0,2,0)的精确解
系统(8)在鞍点B1和B2两侧有无限多个弓形有界轨道,如图2所示.根据引理2,对应于弓形有界轨道,(7)式有一簇紧性解.将h1
(42)
同3.2节中方法一样,(42)式可改写为
(43)
以(v1,0)为初始条件,将(43)式代入(10)式的第一个方程,并积分得
(44)
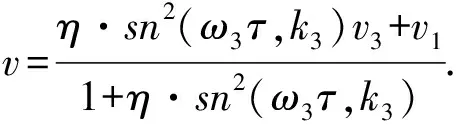
(45)
其中:
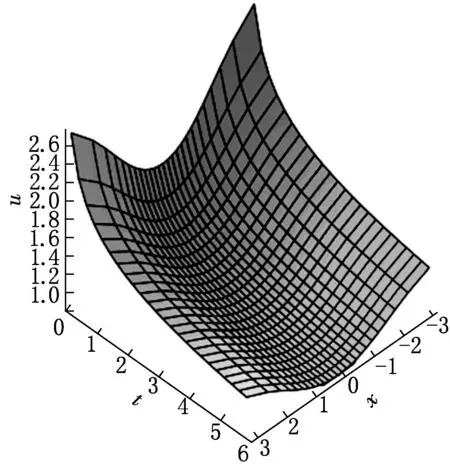
图6 解(47)随时间和空间变量演化的3维图
将(45)式代入变换(9)进行积分,可得
(46)
将(45)式代入(4)式,再结合(47)式可获得方程(3)的一个精确解:
(47)
解(47)定义了一类具有compaction性的渐进稳定解.为了直观地显示解(47)的动力学性质,取参数a0=1,a1=0.5,β=2,α=0.25,t∈[0,6],τ∈[-0.7,0.7],绘制解(47)的动力学曲线,如图6所示.
3.6 在h=h1,β a1Ω>0条件下色散方程Kα(0,2,0)的精确解

(48)

将(48)式代入系统(8)的第一个方程中,并沿通过点(vm,0)的闭轨道积分得
(49)
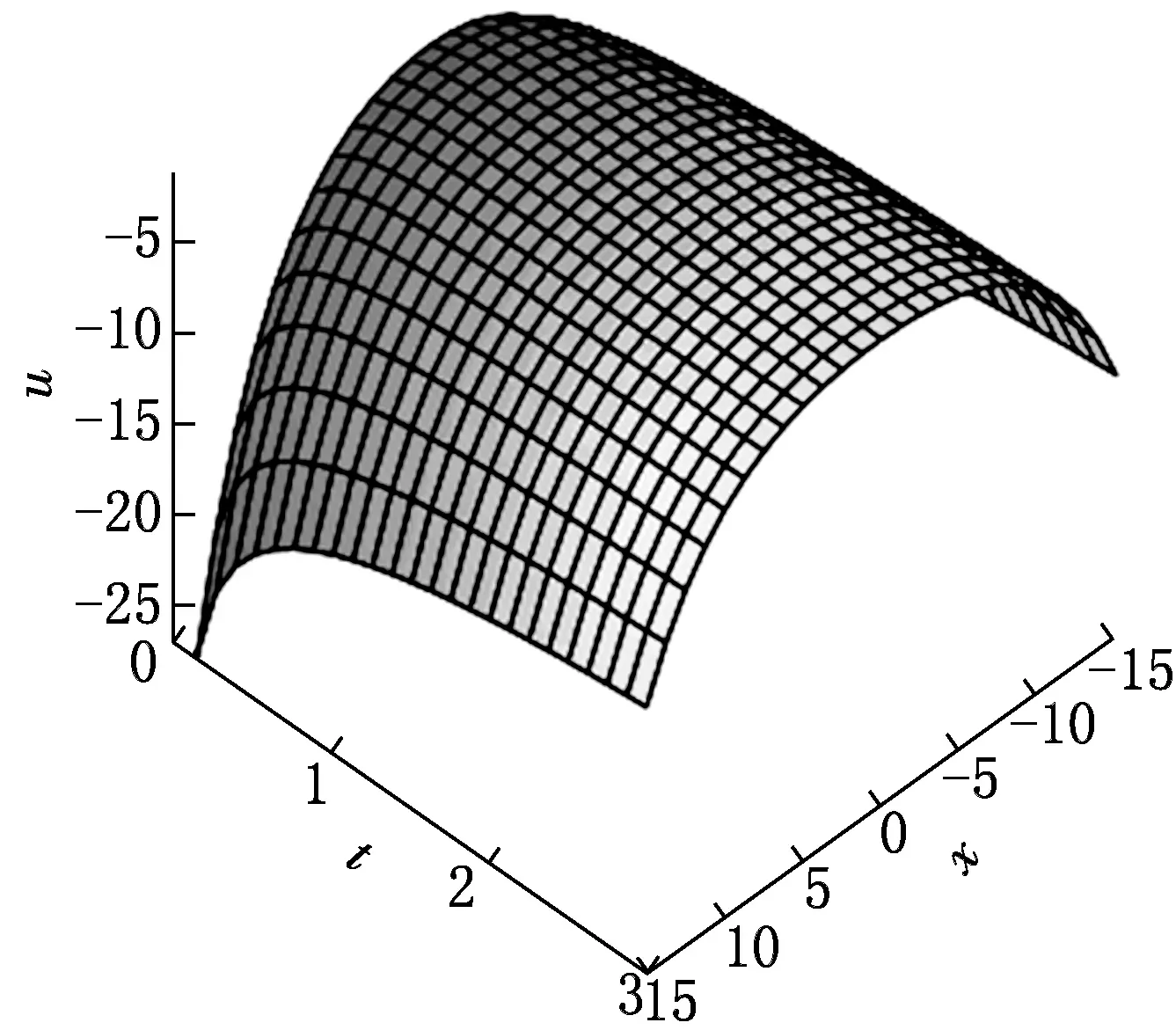
图7 解(51)随时间和空间变量演化的3维图
求解(49)式,可得(7)式的一个无界解
(50)
(51)
当t→+∞时,u→0,故解(51)为无界渐进稳定解.为了直观地显示解(51)的动力学性质,取a0=a1=1,β=2,α=0.25,x∈[-15,15],t∈[0,3],绘制解(51)的动力学曲线图,如图7所示.
4 结论
本文利用分离变量法和动力系统法相结合的方法,研究了非线性时间分数阶色散方程精确解的存在性问题及动力学性质.在一些特殊的参数条件下,得到了时间分数阶色散方程不同类型的精确解,其中有些具有周期性,如解(20)、(27),有些具有compaction性质,如解(32)、(47),有些解具有无界特性,如解(51).它们大多具有随时间增加而衰减的特性,满足当t→+∞时,u→0.
