基于水生系统的常微分方程平衡点的定性分析

刘 煦，陈思潼

(1.吉林财经大学应用数学学院，吉林 长春 130117；2.黑龙江大学数学科学学院，黑龙江 哈尔滨 150080)

1 预备知识

藻类是水生生态系统中的重要初级生产者，可以进行光合作用和化学合成[1].藻类的空间结构一般分为上下两层，位于上层悬浮于水中的称为浮游藻类，位于下层生长于水下各种基质表面的称为底栖藻类[2-4].二者共同构成了藻类种群的重要初级生产者，是水生动物的重要食物来源之一，是水体物质和能量循环中重要一环.

营养是藻类生长的必备元素之一.淡水湖泊营养丰富的环境下，因为水中含有大量的磷、氮等元素，大量有机物在水中降解释放出营养元素，促进水中藻类疯狂增长.但藻类死后分解出大量有毒物质，致使水生生物由于缺氧或中毒而大量死亡，这样就破坏了整个淡水湖泊的生态系统[5].因此，研究藻类和营养的数学模型具有重要的实际应用价值.

近年来，国内外许多学者已经建立并研究了藻类和营养的数学模型，得到了许多优秀的研究成果[2，6-10].本文参考文献[3]建立了一个浅水生态系统中浮游藻类-底栖藻类-营养常微分方程模型：

(1)

其中:U，V分别表示浮游藻类和底栖藻类种群密度；R，W分别是水中浮游层营养和底栖层营养；ru，rv表示种群的内禀增长率；mu，mv分别表示种群U和V的死亡率；Rsur是外界营养输入；Wsed是底层沉淀物释放出的营养；L1，L2表示水中浮游层和底栖层的水深；a，b，c分别表示浮游层营养和底栖层营养、底泥中营养和底栖层营养、外界营养与浮游层营养之间的交换率；η表示浮游藻类的下沉率；γu，γv是半饱和系数；cu，cv是藻类的碳磷比；βu，βv表示藻类死亡后的营养释放率.鉴于模型(1)的实际生物意义，假设模型(1)的初始值都是正的，即U(0)>0，V(0)>0，W(0)>0，R(0)>0.

2 平衡点存在性与稳定性

研究模型(1)的平衡点的存在性及稳定性.模型(1)的平衡点如下：

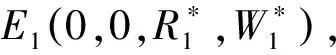
(2)

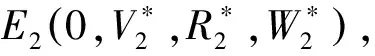
(3)

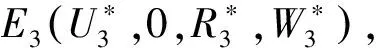
(4)

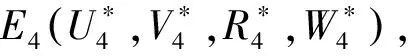
(5)

为了判断这些平衡点的局部渐近稳定性，需要考虑模型(1)的Jacobian矩阵.经简单计算可得模型(1)的Jacobian矩阵为

其中：

其余元素均为0.

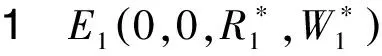
(6)

时，E1是局部渐近稳定的.

证明通过求解方程(2)，可得

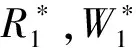
因而当(6)式成立时，有

这说明J(E1)的特征根均具有负实部，因此，E1是局部渐近稳定的.

定理2 若

(7)

(8)

时，E2是局部渐近稳定的.

证明通过求解方程(3)，可得

注意到

考虑特征多项式

f(λ)=|λI-A|=λ3+A1λ2+A2λ+A3，

其中：

所以，当(8)式成立时，有Ai>0，i=1，2，3，A1A2-A3>0，于是J(E2)的特征根均具有负实部.因此，E2是局部渐近稳定的.

那个时候的我们，不谈学业，不言前程。不说喜欢，也不言爱情。自自然然，简简单单，一袋零食，两三本书，就可以去到学校后面的小山坡上坐上半天，说说话，发发呆。没有未来，我们便不谈未来。只谈《梅花三弄》，只谈《七剑下天山》……

定理3 若

则E3存在，并且当

(9)

时，E3是局部渐近稳定的.

证明通过解方程(4)，可得

在E3处的Jacobian矩阵为

考虑特征多项式

g(λ)=|λI-B|=λ3+B1λ2+B2λ+B3，

其中：

若条件(9)成立，易知

Bi>0，i=1，2，3，B1B2-B3>0，

这说明J(E3)的特征根均具有负实部，因此，E3是局部渐近稳定的.

定理4 若

(10)

则E4存在且是局部渐近稳定的.

证明通过求解方程(5)，可得

若条件成立，则E4存在.直接计算有

其特征多项式为h(λ)=λ4+C1λ3+C2λ2+C3λ+C4，其中：

易证若(10)式成立，则

因而，J(E4)的特征根均具有负实部.于是E4是局部渐近稳定的.

3 数值模拟

取γu=3，γv=5，cu=0.008，cv=0.015，βu=0.5，βv=0.3，ru=1，rv=1，η=0.1，L1=2，L2=0.01，a=0.05，b=0.05，c=0.01，Wsed=0.03，Rsur=0.3.

经计算得模型(1)的平衡点，见图1.在图1(a)中，E1是一个稳定的平衡点，意味着U，V种群都灭绝；图1(b)中，E2是一个稳定的平衡点，表示底栖藻类V灭绝；图1(c)中，E3是一个稳定的平衡点，表示浮游藻类U灭绝；图1(d)中E4是一个稳定的平衡点，表示所有种群共存.以mu，mv为参数，建立了平衡点的分布图，见图2，其中：

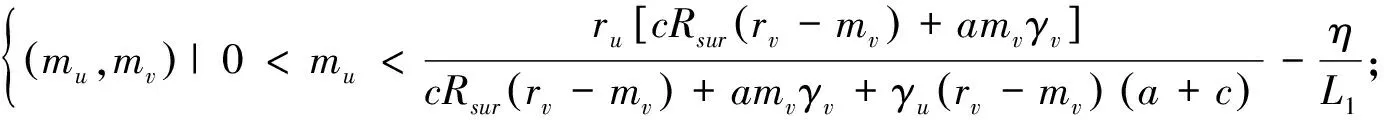
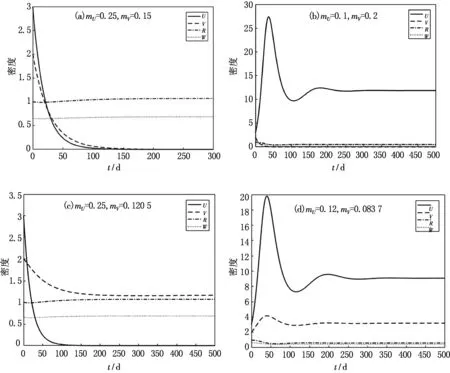
图1 模型(1)的平衡点

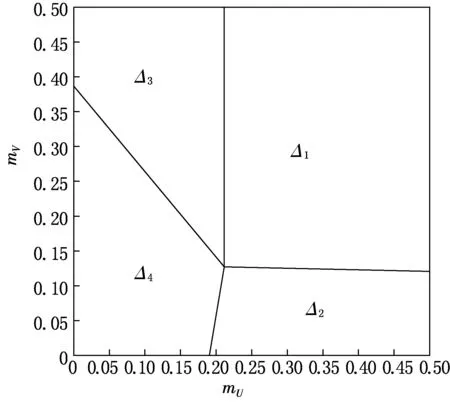
图2 模型(1)的平衡点分布图