X掺杂团簇Bn+1(n=1～11; X=Be, Mn)的密度泛函理论研究

王必利，陈 宣，宋 蕊，秦 猛

(1.陆军工程大学基础部, 南京 211101; 2南京信息工程大学，南京 211101)

1 引 言

硼团簇因其独特的物理特性、良好的化学稳定性而受到广泛的关注，研究表明不同大小的硼团簇具有平面、准平面、管状、笼型或其它三维结构[1-5].硼团簇中掺入杂质原子将显著改变团簇的物理、化学性质[6-15].因而，掺杂硼团簇的研究成为现代团簇科学的前沿热点.刘火雁等[6]研究了CoBn(n≤19)的团簇结构、电子性质和磁性.结果表明，Co的掺杂增强了硼团簇的化学活性，团簇最低能量结构的总磁矩主要来自Co的3d轨道贡献.李世雄等人[10]研究了掺Be 硼团簇BeB0/-1(n= 10～15)的基态结构和性质.结果表明，阴离子比相应中性团簇的稳定性强.阮文等人[11]研究了BnY(n=1～11)团簇的结构和电子性质.结果表明，随着尺寸的增大，团簇的最低能量结构从平面逐步演变为立体结构，基态 B3Y, B5Y ,B7Y 具有较好的稳定性.雷雪玲等人[12]研究了 BnNi(n≤ 5)小团簇的结构和磁性.结果表明，Ni掺入B团簇后增大了其结合能,Ni原子磁矩和团簇总磁矩随团簇尺寸增大而呈现振荡趋势.Saha等[14]研究了金属M掺杂团簇MB12-1(M= Co, Rh).结果表明，团簇MB12-1掺杂后其化学活性得到了增强.

当前，掺杂硼团簇的研究多为单一掺杂，或多种元素原子掺杂同尺寸硼团簇.而不同原子掺杂不同尺寸的硼团簇研究少有报道.为了研究金属原子Be与过渡金属原子Mn替代掺杂硼团簇后, 团簇性质随尺寸的生长变化，课题组对Bn+1X(n=1～11;X=B, Be, Mn)的基态结构、稳定性、电子构型与磁性开展了系统研究，希望能为新型材料的设计提供理论上的参考.

本文全部计算工作使用Dmol3[17,18]程序包进行, 所有计算均设定为自旋非限制, 并且没有设置任何对称性限制;在广义梯度近似(GGA)中,交换关联势采用PerdewWang(1991)NLDA function(PW91)方法，价电荷设定为0; 采用了精度较高的双数值轨道基组+轨道极化函数(DNP)进行了结构优化, 结构优化的收敛标准为:能量阈值2×10-5Hartree(1 Hartree=27.21 eV), 力场0.004 Hartree/Å, 最大位移0.005 Å.结构优化过程中，我们对自旋和对称性均不作限制.为了得到纯硼团簇的最低能量结构,对不同尺寸的团簇, 我们考虑了若干的可能初始结构.对于电子数为奇数的体系，每一种可能结构都进行了自旋多重态为2、4、6、8情况下的优化; 对于电子数为偶数的体系，每一种可能结构都进行了自旋多重态为1、3、5、7情况下的优化.为了得到掺杂硼团簇的最低能量结构，考虑了X(X=Be, Mn)替代团簇Bn(n=2～12)基态和亚稳定构型中不同位置的单个硼原子.所有基态构型均为能量最低且无虚频.

为比较GGA近似与LDA近似对团簇的实用性，我们分别采用这两种泛函计算了B2的键长、振动频率和结合能并与实验结果相比较.结果表明，GGA的PW91泛函计算得到的键长为1.590 Å、振动频率为1065 cm-1、结合能为1.659 eV，与实验值1.59 Å、1051.3 cm-1、1.54 eV[19]最为接近；LDA的PWC泛函计算的键长为1.624 Å、振动频率为1031.5 cm-1、结合能为1.74 eV与实验值最为接近.比较发现GGA-PW91方法与实验值符合最好, 说明本文所选用的计算方法是较合适的.

3 结果与分析

表1给出了团簇BnX(n=1～11;X=B, Be, Mn)的基态结构，表中方括号内的第1项为对应团簇基态构型的自旋多重度，第2项为对称性结果.表2给出了B-X键的平均键长与B-X模式的最高振动频率.

表1 团簇BnX(n=1～11; X=B, Be, Mn)的最低能量结构(大球表示Mn，小球表示Be，其余表示B)，球附近的数值为原子的密立根电荷，方括号中的第1项为自旋多重度，第2项为团簇对称性

B2、BBe、BMn的键长分别为1.564、1.747 和1.767 Å, 掺杂Be，Mn原子后团簇键长均变长，键长变长相互作用减小，这与B2结合能最大为1.660 eV以及BBe结合能最小为0.663 eV相一致.

B2X(X=B, Be, Mn)的基态结构均为三角形结构，B3键长为1.604 Å.B2Be中B-Be平均键长为1.821 Å，B-B键长1.587 Å，小于B3中B-B平均键长.这表明Be替代掺杂B3团簇后，B-B之间相互作用加强了, 与表2中的B-B模式振动频率相吻合.B2Mn中B-B键长1.609 Å，B-Mn平均键长为1.902 Å，大于B2Be中B-Be平均键长.这表明B-Mn 相互作用弱于B-Be相互作用, 与频率分析相符.

B4为菱形结构，B-B平均键长为1.644 Å.团簇B3X(X=Be, Mn)都是X替代B4中配位数为2的硼原子而生成的四边形结构.B3Be中B-B平均键长与B-Be平均键长分别为1.588和1.774 Å.B3Mn中B-B平均键长与B-Mn平均键长分别为1.606和1.938 Å.

B5为蝶型结构，可看作在团簇B4的桥位接单个硼原子生成，B-B平均键长为1.649 Å.团簇B4X(X=Be, Mn)都是X替代B5中配位数为2的硼原子生成的五边形结构.B4Be中B-B平均键长与B-Be平均键长分别为1.728和1.758 Å.B4Mn中B-B平均键长与B-Mn平均键长分别为1.644和1.846 Å.

B6为五角带帽结构.B5Be是Be替代B6中配位数为5的帽位硼原子生成的畸变五角带帽结构.B5Mn的基态结构是在B5的桥位接Mn原子生成.团簇B5Be中的B-B平均键长最短为1.601 Å，B5Mn中的B-B平均键长最长为1.667Å.这说明Be替代掺杂B6后B-B相互作用加强，Mn替代掺杂B6后B-B相互作用减弱.B-Be平均键长为1.939 Å, 大于B-Mn的平均键长1.925 Å.这说明B5Be中B-Be相互作用弱于B5Mn中B-Mn相互作用.

B7与B6Be都是六角带帽结构, 对称点群分别为C2v和C6v.B6Be由Be替代B7帽位原子生成.B6Mn是在B5Mn的B3与B4桥位接一个B原子生成.B6Be中的B-B平均键长最短为1.577 Å，B7中的B-B平均键长最长为1.685Å.B-Be平均键长为1.925 Å, 小于B-Mn的平均键长2.081 Å.

B8为对称为D7h的正七边行结构.B7X(X=Be, Mn)均为六角双帽结构.X位于配位数为6的帽位.键长结构表明X替代掺杂B8后，团簇中B-B相互作用加强了.B-Be平均键长为1.974 Å, 小于B-Mn的平均键长2.133 Å.这与B6X的结果一致.

B9为对称为D7h的七角双锥结构.B8X均为对称群为C7v的七角双帽结构结构.X位于配位数为7的帽位.B9中的B-B平均键长最短为1.664 Å.这说明X掺杂B9后B-B相互作用减弱.

B10为准面状结构.团簇平均键长为1.681 Å.B9Be为Be替代B10中B6生成对称群为Cs的准面状结构.B-B平均键长为1.641 Å.B9Mn为对称群为D9h的九边形结构.Mn原子处于配位数为9的团簇中心位置.B-B平均键长为1.542 Å.B-B键长结果说明，Mn原子相较于Be原子掺杂B10，更能提高B-B相互作用.

B11为对称群是C2v的面状结构.B10X均为对称群为Cs的准面状结构.X均位于配位数为7的高配位.B10Be中B-B平均键长最短，为1.651 Å；B10Mn中B-B平均键长最长，为1.684 Å.这说明Be掺杂B11增强了B-B相互作用，Mn原子掺杂则减弱了B-B相互作用.

B12为对称群是C3v的准面状结构.B-B平均键长为1.564 Å.B11Be为Be替代B12中B7生成，对称群为Cs的准面状结构.Be原子配位数为6.B-B平均键长为1.676 Å.B11Mn为对称群是Cs的准面状结构, 可以看成由B10Mn中B9与B10断键与B12成键生成.Mn位于原子配位数为8的高配位.

上述计算结果表明：除B6和B9为体结构外，纯硼团簇Bn+1(n=1～11)均为面状或准面状结构.BnBe(n=1～11)的稳定结构均由Be原子掺杂团簇Bn+1得到.而BnMn(n=1～6, 10, 11)的稳定结构则可看成是由Bn-1Mn(n=1～6, 10)生成.团簇BnX(n=5～11;X=Be, Mn)中的X原子均位于高配位.Bn+1与BnBe的基态构型为多重度为1或2的自旋低重态.n取奇数时，团簇BnMn(n=2～11)基态的多重度为1.这表明团簇BnMn(n=2～11)基态构型的自旋多重度随团簇尺寸的变化而具有奇偶震荡性.

3.2 稳定性分析

为了研究硼团簇替代单掺杂铍原子或锰原子对团簇相对稳定性的影响，课题组计算了BnX(n=1～11;X=B, Be, Mn)基态结构的B-X(X=B, Be, Mn)平均键长、B-X模式的最高振动频率、平均结合能Eb、HOMO-LUMO能隙Egap、离解能Ed和二阶差分能ED2，具体计算结果见表2和表3.Eb、Ed、ED2定义式为：

表2 Bn+1和BnX(X=Be, Mn)中B-B模式的最高振动频率和B-B平均键长，以及BnX(X=Be, Mn)中B-X模式的最高振动频率和B-X平均键长

表3 团簇BnX(n=1～11; X=B, Be, Mn)基态结构的结合能Eb、能隙Egap、离解能Ed和二阶差分能ED2

Eb[BnX]=[nE(B)+E(X)]/(n+1)

(1)

ED2[BnX]=E(Bn+1X)+E(Bn-1X)-2E(BnX)

(2)

Ed[BnX]=E(Bn-1X)+E(B)-E(BnX

(3)

图1给出了BnX(n=1～11;X=B, Be, Mn)中B-X平均键长随尺寸变化的规律.从图1我们可以看出，B-X平均键长随着团簇尺寸变化规律相同.这与团簇结构变化规律一致.键长变化反映出结构变化，键长变化越大，结构改变越显著.这与表1给出的结构变化相吻合.X(X=Be, Mn)原子位于高配位时，B-X平均键长较大，体结构团簇的B-X平均键长也较大.例如，团簇BnX(n=8;X=B, Be)中, B-X平均键长局域最大.面结构或准面结构团簇中的B-X平均键长较短.例如，团簇B12的平均键长最短，表明纯硼团簇中B12的B-B相互作用最强.这与刘立仁等[3]采用B3LYP方法得出B12为幻数团簇结论吻合.原子数目相同时，Bn+1中B-B平均键长最短，BnMn中B-Mn平均键长最长.这表明掺杂原子与B原子的相互作用弱于纯硼团簇中B-B相互作用.我们从图1中得到的一个有趣结果是: 含有8个B原子的团簇其B-X平均键长最大.

图1 团簇BnX(n=1～11; X=B, Be, Mn)基态结构的最高振动频率

团簇研究中, 常常用振动频率来描述成键原子间的相互作用强弱.振动频率越高, 相互作用越强[20].图2比较发现，随着尺寸的增大，团簇BnX(n=1～11;X=B, Be, Mn)的最高振动频率增加.这说明随着团簇的生长其稳定性加强；原子数目相同时，团簇Bn+1最高振动频率总体上较高.

图2 团簇BnX(n=1～11; X=B, Be, Mn)基态结构中B-X的平均键长

从图3我们可以看出，随着团簇尺寸的增大，BnX(n=1～11;X=B, Be, Mn)的平均结合能逐渐增大.这表明其稳定性随尺寸的增大而增大.这与最高振动频率结果分析一致.此外，从图3可见，平均结合能增幅逐步减小.原因在于，随着团簇尺寸的增长，原子的配位数增加，原子之间的差异逐渐缩小，从而使得构成团簇的原子间的相互作用趋于稳定.原子数目相同时，Bn+1团簇的平均结合能最高.这与键长、频率分析一致，说明纯硼团簇单掺杂铍原子、锰原子均降低了团簇原子间相互作用，不利于团簇的稳定.从图3我们还可以看出团簇BnX(n=8;X=B, Be, Mn)的平均结合能相差最小.这与图2最高振动频率结果完全一致.

图3 团簇BnX(X=B, Be, Mn, n=1～11)基态构型的平均结合能

离解能可以很好地反映团簇的稳定性.图4给出了BnX(n=1～11;X=B, Be, Mn)的离解能Ed随团簇尺寸的演化规律.由式(3)可知，若离解能结果大于零，表明团簇解离出一个硼原子需吸收热量，反之则放出热量.从图4我们可以看出：BnX的离解能均为正，表明团簇生长过程都是放热反应；原子数目相同时，团簇Bn+1的离解能最大.这说明纯硼团簇掺杂铍原子或锰原子后易失去B原子.这与平均结合能结果一致.

图4 团簇BnX(n=1～11; X=B, Be, Mn)基态构型的离解能

二阶差分能反应了团簇的相对稳定性高低.从图5我们可以看出：面状构型团簇Bn+1(n=2, 4, 7, 9)较相邻的团簇稳定性高，BnBe(n=2, 4, 8, 10)的稳定性高于邻近团簇, BnMn(n=3, 5, 7, 10)较相邻的团簇稳定性高.结果表明团簇尺寸较小时，Bn+1与BnBe的相对稳定性变化规律一致；尺寸较大时，BnBe与BnMn相对稳定性结果一致，这可能是随着团簇尺寸的增长，原子的配位数也在增加，原子之间的差异逐渐缩小导致.总体表明纯硼团簇掺杂后的相对稳定性变化与掺杂原子和团簇尺寸都有关.

图5 团簇BnX(n=1～11; X=B, Be, Mn)基态结构的二阶差分能

能隙反映了团簇的化学活性, 是考察物质导电性的参数.能隙越大, 团簇化学活性越低; 能隙越小, 团簇化学活性越高.图6给出了BnX(n=1～11;X=B, Be, Mn)的能隙随团簇尺寸的演化规律, 从图6我们可以看出: 总体上，原子数目相同时Bn+1的能隙高于掺杂团簇.这说明掺杂铍原子或锰原子有利于提高纯硼团簇的化学活性.B12的能隙局域最大，这与平均结合能结果一致.n<10时，BnX(X=B, Mn)的能隙变化规律一致.这可能与B原子以及Mn原子最外层电子为半满排布有关.

图6 团簇BnX(n=1～11; X=B, Be, Mn)基态结构的能隙

HOMO与LUMO轨道是决定一个体系能否发生化学反应的关键.因此，我们十分有必要对团簇的前线轨道进行研究.图7给出了部分团簇的HOMO与LUMO轨道图.从图7我们可以看出，团簇B10的HOMO轨道为明显的π轨道.团簇B9Be的HOMO轨道阴影面积相较B10的HOMO轨道阴影面积更大.这说明掺杂Be原子后，HOMO轨道成键电子的活动区域增大，即团簇B9Be的HOMO轨道给出电子的能力也更强.团簇B9Be的化学活性较团簇B10的化学活性强.团簇B10Be的HOMO轨道为明显的π轨道.纯硼团簇B11的HOMO轨道电子的离域性明显，表明团簇B11掺杂Be原子后，HOMO轨道给出电子的能力减弱，Be原子掺杂团簇B11，有利于提升团簇的化学稳定性.对于团簇BnMn(n=9～11)的HOMO与LUMO则主要由Mn原子的花瓣状的3d轨道以及B原子的2s, 2p组成.图6的能隙结果表明，spd杂化使得Mn原子掺杂团簇Bn+1(n=9～11)得到的体系能隙变小.

图7 团簇BnX(n=9～11; X=B, Be, Mn)基态构型的HOMO与LUMO图

3.3 电子性质与磁性分析

表4给出了团簇BnX(n=1～11;X=B, Be, Mn)中B 2s, 2p、Be 2s, 2p, 3d、Mn 3d, 4s, 4p轨道的密立根电荷分布，自由B原子的外层电子排布为2s22p1,自由Be原子的外层电子排布为2s2,自由Mn原子的外层电子排布为3d54s2.从表4我们可以看出:纯硼团簇Bn+1中B原子的2s轨道失去电荷为0.612e～0.821e, 2p轨道得到电荷为0.619e～0.764e.这说明B原子的2s电子主要转移到2p轨道，少量转移到3d轨道，表现出显著的2s2p杂化和微弱的2s3d杂化.团簇B2中B原子的2s与2p轨道之间电荷转移最少，则原子间2s2p杂化最弱，B原子之间相互作用最弱.这与纯硼团簇中B2的平均结合能、解离能最小相一致.

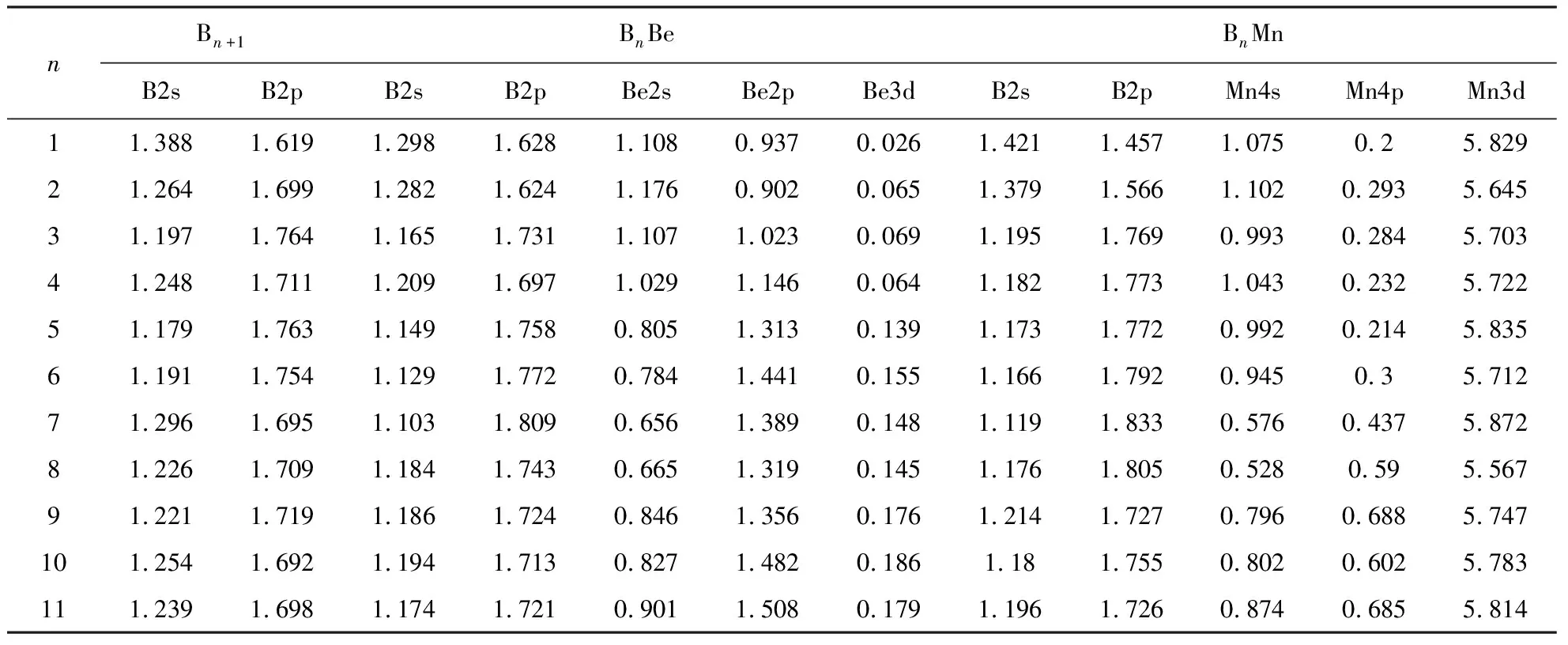
表4 团簇BnX(n=1～11; X=B, Be, Mn)中的B 2s, 2p，Be 2s, 2p, 3d和Mn 3d, 4s, 4p轨道的有效电荷(e)分布

团簇BnBe中B原子的2s轨道失去电荷为0.702e～0.897e, 2p轨道得到电荷为0.624e～0.809e，Be原子的2s轨道失去电荷为0.892e～1.344e, 2p轨道得到电荷为0.902e～1.508e，3d轨道得到电荷0.026e～0.186e.这说明B原子的2s电子除了主要转移到2p轨道，少部分还转移到Be原子的2p轨道与3d轨道.这与表1的团簇BnBe中Be原子均得到电子的情况吻合.而电荷从B转移到Be, 形成成键轨道有助于团簇的稳定.

团簇BnBe(n=2～4)均为平面结构, Be原子配位数都是2，B4Be中Be原子得电荷量最大为0.234e，B2Be中Be原子得电荷量最少为0.141e.由表2振动频率与键长结果可知, B4Be中B-Be模式振动频率最大，为1059 cm-1; B2Be中B-Be模式振动频率最小，为792cm-1.团簇BnBe(n=6, 7)对称性都是C6v, Be原子配位数都是6.B6Be中Be原子得电荷量较大，为0.379e; B7Be中Be原子得电荷量相对较少，为0.127e.B6Be中B-Be模式振动频率较大，为1033 cm-1; B7Be中B-Be模式振动频率较小，为792 cm-1.团簇BnBe(n=9, 11)对称性都是Cs, Be原子配位数都是6.B11Be中Be原子得电荷量较大，为0.589e; B9Be中Be原子得电荷量相对较少，为0.377e.B11Be中B-Be模式振动频率较大, 为860 cm-1; B9Be中B-Be模式振动频率较小, 为828 cm-1.一般而言, 原子间振动频率越高说明相互作用越强.以上结果表明：团簇构型相同、Be原子配位数相同时，Be得到的电荷量越大，B-Be模式的相互作用就越大.

团簇BnMn中B原子的2s轨道失去电荷为0.579e～0.881e, 2p轨道得到电荷为0.457e～0.883e.我们通过比较发现，团簇BnMn中B原子2s2p轨道杂化弱于团簇BnBe中B原子2s2p轨道杂化.这表明BnMn中B-B相互作用弱于BnBe中B-B相互作用，与图2团簇BnMn中 B-B模式最高振动频率总体小于BnBe中B-B模式最高振动频率的情况相吻合.Mn原子的4s轨道失去电荷为0.898e～1.472e, 4p轨道得到电荷为0.2e～0.688e，3d轨道得到电荷0.567e～0.872e.团簇BnMn中Mn原子轨道电子表现出显著的4s4p3d杂化.

表5给出了团簇BnX(n=1～11;X=B, Be, Mn)总磁矩，B 2s, 2p,Be 2s, 2p 和Mn 3d, 4s, 4p轨道磁矩.从表5我们可以看出, 开壳层结构团簇BnX(X=B, Be)的磁矩主要由2p轨道贡献.纯硼团簇Bn+1(n=3, 5, 9, 11)为闭壳层结构.这是由于自由B原子的外层电子排布为2s22p1，n取奇数时，体系的电子数为偶数，每一个自旋向上α电子都有一个自旋向下的β电子与之配对，因此空间任意位置处α电子与β电子密度相同.对于同为偶数电子体系的团簇Bn+1(n=1, 7)，由于自旋极化，α电子与β电子轨道不完全重叠，导致总磁矩不为零.团簇BnBe(n=4, 6, 8, 10)为闭壳层结构.这是由于自由Be原子的外层电子排布为2s2，n取偶数时，体系的电子数为偶数.团簇B2Be总磁矩不为零，也是由电子自旋极化导致的.

表5 团簇BnX(n=1～11; X=B, Be, Mn)的总磁矩(μB)，以及B 2s, 2p, Be 2s, 2p 和Mn 3d, 4s, 4p的轨道磁矩(μB)

团簇BnMn(n=1～11)均为开壳层结构.很明显, 团簇总磁矩主要由Mn3d轨道磁矩贡献.总体上3d轨道磁矩越大，团簇磁矩越大.团簇BnMn(n=7, 9～11)的Mn3d轨道磁矩相对较小，这是因为对应团簇中Mn原子均处于高配位，而过渡金属原子配位数越高，团簇的局域d电子态越宽，越不易发生自旋劈裂，从而形成较多自旋平行的d电子态[7].团簇B8Mn中Mn原子虽也处在高配位，但其3d轨道磁矩却最大，为4.20μB.这是因为过渡金属元素的磁性除了受原子配位数影响，还受平均键长影响.平均键长越长，原子间波函数重叠越少，越能保持自由原子的磁矩.自由Mn原子的3d轨道磁矩为4.899μB.由表2可见，团簇B8Mn中的B-Mn平均键长最长，为2.461 Å，而团簇B11Mn中Mn3d轨道磁矩最小为2.447μB.这是由于B11Mn中Mn原子的配位数最高(为8)，且B-Mn平均键长局域较短(为2.137 Å).团簇BnMn(n=2～6)的Mn3d轨道磁矩相对较大且大小接近，这是由于团簇中Mn原子的配位数相同(均为2)，且B-Mn平均键长接近.总体上随着团簇BnMn尺寸的增大，Mn原子的配位数增大.B-Mn平均键长增大，Mn3d轨道磁矩减小而导致团簇的总磁矩减小.

Jahn-Teller定理表明开壳层结构的团簇为了降低能量、消除简并度，存在形变和提高稳定性的可能[21].这与之前的能隙结果相吻合.对比表5与图6, 我们发现原子数目相同时，电子构型为闭壳层的团簇其能隙相对较大，且化学活性最低.

为了直观地表明不同掺杂对团簇磁性的影响，图8给出了一些团簇(B12、B11Be、B11Mn)的自旋分波态密度(Partial density of states, PDOS).图8中的实线与虚线分别代表自旋向上的α电子与自旋向下的β电子在不同能量范围内的分布.团簇磁性是由未配对的电子(即净剩的α 电子或净剩的β电子)提供的.实线、虚线两条态密度曲线对能量的积分之和即是该轨道的成单电子数.其中自旋向上电子的态密度曲线对能量的积分为正值，而自旋向下电子的态密度曲线对能量的积分为负值.态密度曲线的对称性越好，自旋向上和自旋向下的电子对能量的积分值就越趋向于大小相等、符号相反，则该轨道上的成单电子数越少.如图8a所示，团簇B12在s、p、d轨道的自旋态密度分布关于横轴对称, 表明s、p、d轨道的自旋磁矩为零，因此团簇B12的磁矩为零.如图8b所示，单个Be原子替代掺杂团簇B12中的6配位硼原子后，s、p、d轨道的自旋态密度分布关于横轴不完全对称，产生了自旋轨道极化.很明显p轨道的单电子最多，即p轨道磁矩对总磁矩贡献最大.如图8c所示, 团簇B11Mn的d轨道的电子自旋态密度分布相较于其他3个轨道，其对称性最差.我们通过比较，发现团簇的d轨道电子由Mn原子3d 轨道贡献，即团簇B11Mn的总磁矩由Mn原子3d 轨道贡献，d轨道的电子自旋态密度分布没有明显的最高峰，而是由多个小峰组成.这表明团簇B11Mn中Mn原子3d 轨道的电子退局域化明显，这也是B11Mn的总磁矩相对较小的原因.

图8 团簇的电子分波态密度:(a)B12;(b)B11Be;(c)B11Mn

4 总 结

为了比较金属原子Be与过渡金属原子Mn替代掺杂硼团簇后，团簇的性质随尺寸的生长变化，本文对Bn+1X(n=1～11;X=B, Be, Mn)的基态结构、稳定性、电子构型与磁性开展了系统研究.结论如下:

(1)BnBe的稳定结构均由Be原子掺杂团簇Bn+1得到，而BnMn(n=1～6, 10, 11)则可看成是由Bn-1Mn(n=1～6, 10)生成.团簇BnX(n=5～11;X=Be, Mn)中的X原子均位于高配位.BnBe的基态构型为多重度为1或2的自旋低重态, 而团簇BnMn基态构型的自旋多重度随团簇尺寸的变化具有奇偶震荡性.键长分析结果表明，含有8个B原子的团簇其B-X平均键长最大.

(2)平均结合能结果表明，随着团簇尺寸的增大，BnX(n=1～11;X=B, Be, Mn)的平均结合能都逐渐增大，但增幅逐渐减小.原子数目相同时，Bn+1团簇的平均结合能最高.离解能结果表明，纯硼团簇掺杂铍原子、锰原子后易失去B原子.二阶差分能结果表明，纯硼团簇掺杂后的相对稳定性变化与掺杂原子和团簇尺寸都有关.能隙结果表明，掺杂铍原子、锰原子有利于提高纯硼团簇的化学活性，B12为幻数团簇.

(3)Mulliken电荷分析表明，团簇BnBe中的Be原子是电荷的受体，团簇BnMn中Mn原子轨道电子表现出显著的4s4p3d杂化.磁性分析表明，开壳层结构团簇BnX(X=B, Be)的磁矩主要由2p轨道贡献.团簇BnMn均为开壳层结构，总磁矩主要由Mn3d轨道磁矩贡献.随着团簇BnMn尺寸的增大，Mn原子的配位数增大，B-Mn平均键长增大, Mn3d轨道磁矩减小而导致团簇的总磁矩减小.