基于改进SA-WOA算法优化热封刀温度控制系统PID参数的研究

魏上云，马 靖，胡晓兵，李 虎，郭 爽，章程军

(1.四川大学机械工程学院，成都 610065；2.四川省宜宾普什集团有限公司技术中心，宜宾 644007；3.四川大学宜宾园区，宜宾 644000)

全自动套袋机是一种将具有热塑特性的薄膜通过热封刀加热裁切制成包装袋，并自动套装在产品上的机器[1].热封质量的好坏直接影响产品的后续加工.热封质量与热封温度、热封压力以及热封时间相关联，其中热封温度对于热封质量的影响最大[2，3]，因此对热封温度控制的研究尤为重要.

目前温度控制最为普遍的方式为比例-积分-微分(Proportional-Integral-Derivative，PID)控制，PID控制是控制领域最成熟也最基础的控制方式[4].但是PID控制存在控制参数难以调节的缺点.控制参数直接影响PID控制的效果.目前PID参数的设定大多通过人为经验选取，控制效果不理想.西门子S7-200 SMART PLC中内置的PID模块采用继电反馈算法进行自整定寻优.这种算法首先需要人为设定控制参数，让系统达到平衡，平衡之后，再给定系统一个微小的扰动，根据系统产生的变化计算出最优的控制参数[5].这种算法整定过程复杂，耗费时间过长，且寻优效果不理想.文献[6，7]提出利用粒子群算法找寻最优PID控制参数，以满足实际控制需求.但是粒子群算法计算量大，且有可能找到的是局部最优参数，导致控制效果不理想[8-10].鲸鱼优化算法(Whale Optimization Algorithm，WOA)，是一种智能优化算法，相对于粒子群算法，鲸鱼算法的计算量更小，优化效果更好[11].但是鲸鱼算法也会有进入局部最优的情况存在[12].为了避免这一情况，人们考虑引入模拟退火算法(Simulated Annealing Algorithm，SA).模拟退火算法是一种模拟温度降温过程而引出的算法，它可以有效地避免陷入局部最优[13].文献[14]提出了一种基于模拟退火的改进粒子群算法(Improved Particle Swarm Optimization Based on Simulated Annealing，SACPSO)对PID参数进行整定.本文则将SA算法与WOA算法相结合，提出了一种改进的基于模拟退火的鲸鱼算法(Improved Whale Algorithm Based on Simulated Annealing Algorithm，SA-WOA).该算法可以有效避免陷入局部最优.我们在此基础上改进提升算法的计算效率，将改进后SA-WOA算法进行PID参数自整定寻找最优PID参数，然后将所得参数应用到PID控制器上，实现对套袋机热封刀的温度控制.

2 全自动套袋机温度控制系统

本文对一款自研的TD150全自动套袋机进行研究.全自动套袋机温度控制即是对套袋机的热封刀进行温度控制.套袋机控制器采用西门子S7-200 SMART型号PLC，K型热电偶温度传感器采集热封刀的温度，西门子PLC的EM AT04模拟量输入模块将温度传感器的电压信号转换为数字信号，实时采集温度信息.PLC普通数字量输出口进行PWM脉宽调制控制固态继电器，实现加热管不同功率的加热，完成对热封刀温度的精准控制.PLC与HMI人机界面采用RS485串口通讯，可以实时读取温度传感器的信息，温度数据在界面上显示，可以更直观地检测温度是否到达设定值.PLC与上位机之间采用ISO-TCP通讯[15]，上位机实时读取温度数据，通过温度数据的读取可以得到系统的模型，上位机进行参数自整定，将计算的参数传入PLC控制器.整个控制系统如图1所示.

图1 温度控制系统

热封刀如图2所示，其中传感器安装孔用于安装K型热电偶传感器，加热管安装孔用于安装加热管，加热整个刀体，完成对薄膜的热封.

对于图2所示的热封刀模型，热封刀的热量获取是由加热管产生的热量减去通过刀体散发给环境的热量[16]，因此有如下公式.

(a)热封刀三维模型

(1)

式中，m为热封刀的质量；c为比热容；h为热封刀表面传热系数；S为热封刀与环境交换热量的总面积；T为热封刀当前温度；T′为环境当前温度；Q为热封刀获取的热量.

为了对式(1)进行简化，我们通常在平衡点(Q′，U′)附近将整个热交换过程近似为线性过程，于是有

(2)

将式(1)两边同时除以hS得：

(3)

式中，t′、K均为常数；ΔT为热封刀当前温度与环境当前温度的差值.

因此式(3)为一个微分方程，对式(3)进行拉普拉斯变换，结果可得

(4)

结合实际生产过程，热量的传递过程是一个具有大惯性和大时滞性的过程.因此对式(4)修正可得

(5)

式中，τ为滞后时间.

根据文献[17]介绍，通过阶跃响应曲线法可以得出系统的传递函数.于是我们给定系统一个100%脉宽的输入，通过温度传感器以0.5 s的采样周期采集温度数据，PLC再将温度数据传递到上位机，根据数据得出系统在1400 s左右到达平衡.通过MATLAB的ident工具箱识别出传递函数为

(6)

式(6)中，拟合的传递函数与实测数据的拟合度为94.84%，拟合度较高.拟合曲线与实测数据曲线如图3所示.

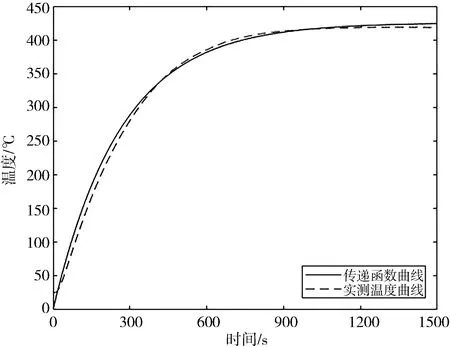
图3 传递函数拟合曲线

3 改进SA-WOA智能优化算法

3.1 PID算法

PID算法的控制原理是将期望值与当前值做差得到误差量，对误差量进行比例、积分、微分运算可以得到一个控制量，将新的控制信号传递给系统进行控制，使实际值不断地接近期望值.比例运算可以适当调整系统达到期望值的时间，比例过大会引起较大的超调，比例过小会导致达到稳态的时间过长.积分运算可以消除系统的稳态误差.微分运算可以提前预知系统超调，减小输出[18,19].一般情况下PI控制即可满足需求.其控制如下式所示.

(7)

式中，KP为比例系数；KI为积分系数；KD为微分系数；e(t)为t时刻的误差量.

因为实际生产中都是对数据进行离散采样，目前使用最广泛的是增量式PID.将式(7)进行离散化处理得到：

Δu(t)=KP(e(t)-e(t-1))+KIe(t)+

KD(e(t)-2e(t-1)+e(t-2))

(8)

在实际控制系统中，更改KP、KI、KD3个参数即可对系统进行控制，但是传统的PID算法中这3个参数是人为根据经验制订的，并不一定是最优的.因此传统的PID算法控制温度系统不是很精确.

3.2 鲸鱼算法

鲸鱼算法是一种智能优化算法，它是模仿鲸鱼捕食的过程而演化出来的算法，具有原理简单、操作简易、易于实现、需要调整的参数少及鲁棒性强的特点.在函数优化方面，鲸鱼算法的求解精度和稳定性要优于粒子群算法、差分进化算法和遗传算法等.鲸鱼捕食采用的是一种泡泡网捕食的方法，这种捕食方法有以下3种表现形式[20]：

(1)包围猎物.

鲸鱼可以识别猎物的位置并将其包围，通过下列方程表现这一过程：

(9)

(10)

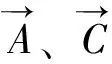
(11)

(12)

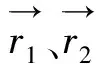
(2)泡泡网攻击.

(13)

式中，b、l为常数.

(3)搜索猎物.

(14)

(15)

3.3 模拟退火算法

模拟退火算法(SA算法)是一种模拟金属退火的原理而衍生出来的算法，它以一定的概率接受比当前解差的解，从而有概率跳出局部最优，具有计算过程简单，通用鲁棒性强的特点.SA算法的计算过程如下[14].

(1)初始化：初始温度T，初始解状态x(迭代起点)，每个温度状态下的迭代次数L.

(2)产生新解xnew=x+Δx，Δx为一个增量范围内的随机数.

(4)判断是否达到该温度下的迭代次数，如果满足迭代次数，则判断是否满足终止条件，满足则停止；如果不满足迭代次数，则继续迭代，满足迭代次数但不满足终止条件的话则继续降温.温度降温过程一般为T=αT，α一般取接近于1的值，如0.95、0.9等.

3.4 算法改进

结合SA算法以及WOA算法的优点，将SA算法与WOA算法结合保证优化结果是全局最优，因此采用SA-WOA算法对PID参数进行整定，理论上可以达到最优的控制效果.我们在此基础上对SA-WOA算法做如下改进.

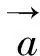
(16)

式中，L表示当前迭代次数；Lmax表示最大迭代次数.

(2)鲸鱼在进行泡泡网攻击时，定义螺旋游动以及向猎物靠近两种方式概率相同，但是在实际中，鲸鱼在前期搜索范围较大的情况下，有较大概率围绕目标螺旋游走继续找寻猎物；在后期距离猎物较近的情况下，有大概率向猎物靠近.因此我们将算法进行以下改进.

(17)

式中，L表示当前迭代次数；Lmax表示最大迭代次数.

(3)模拟退火算法的终止条件通常为温度下降到极低或者误差达到设定需求.本文综合考虑鲸鱼算法的迭代终止条件，将终止条件改为迭代次数的达到，同时对温度的下降过程进行改进，温度下降需要与迭代次数有关.考虑反比例函数关系，改进后的温度下降过程为

(18)

式中，L表示当前迭代次数；Lmax表示最大迭代次数.改进后的算法流程图如图4所示.

图4 改进算法流程

改进后的SA-WOA算法步骤如下所示.

(1)根据温度控制系统的约束条件，初始化鲸鱼种群(数量为m)，包括鲸鱼的位置，以及给定起始温度T0，迭代次数Lmax.

(2)根据适应度函数计算每条鲸鱼的适应度值，并更新最优鲸鱼位置及最优值.

(3)判断是否满足结束条件，如满足则输出最优值，不满足则执行步骤(4).

(6)进行降温操作.

(7)返回步骤(2).

对比文献[14]所用方法，文献[14]采用模拟退火策略对改进粒子群算法进行优化的原理为：当改进粒子群算法进入局部最优，或者达到迭代次数后，再引入模拟退火算法进行二次优化.此种算法属于先利用改进粒子群算法进行粗寻优，再利用模拟退火算法进行精寻优的方式.本文算法与之不同，本文算法将模拟退火算法的思想融入鲸鱼算法中，在鲸鱼算法的每一次迭代中，都进行一次模拟退火策略的判断.本文算法可以加快迭代的速度，减少计算量，且同时保证结果为全局最优.

4 仿真对比实验分析

利用MATLAB R2017b软件进行仿真分析，将改进的SA-WOA算法在软件上编程，适应度函数考虑温度的总误差以及超调量，制订适应度函数为

(19)

式中，c1、c2为权重系数.

制定鲸鱼种群数量为100，迭代次数为100，KP、KI和KD等3个参数的范围依次为[0，10]、[0，10]、[0，10]，系统输入u(i)的范围为[0，100].权重系数c1为0.999，c2为0.001.根据套袋机要求，封膜温度为130 ℃.

由于系统延时不论在何种算法优化情况下都是相同的，因此在进行仿真实验时，它可以忽略不计.实验结果如图5所示，系统在160 s之后系统达到平衡，且整个过程中，系统的超调量为0.实验结果表明，本文算法优化的参数值可以很好地控制系统温度.

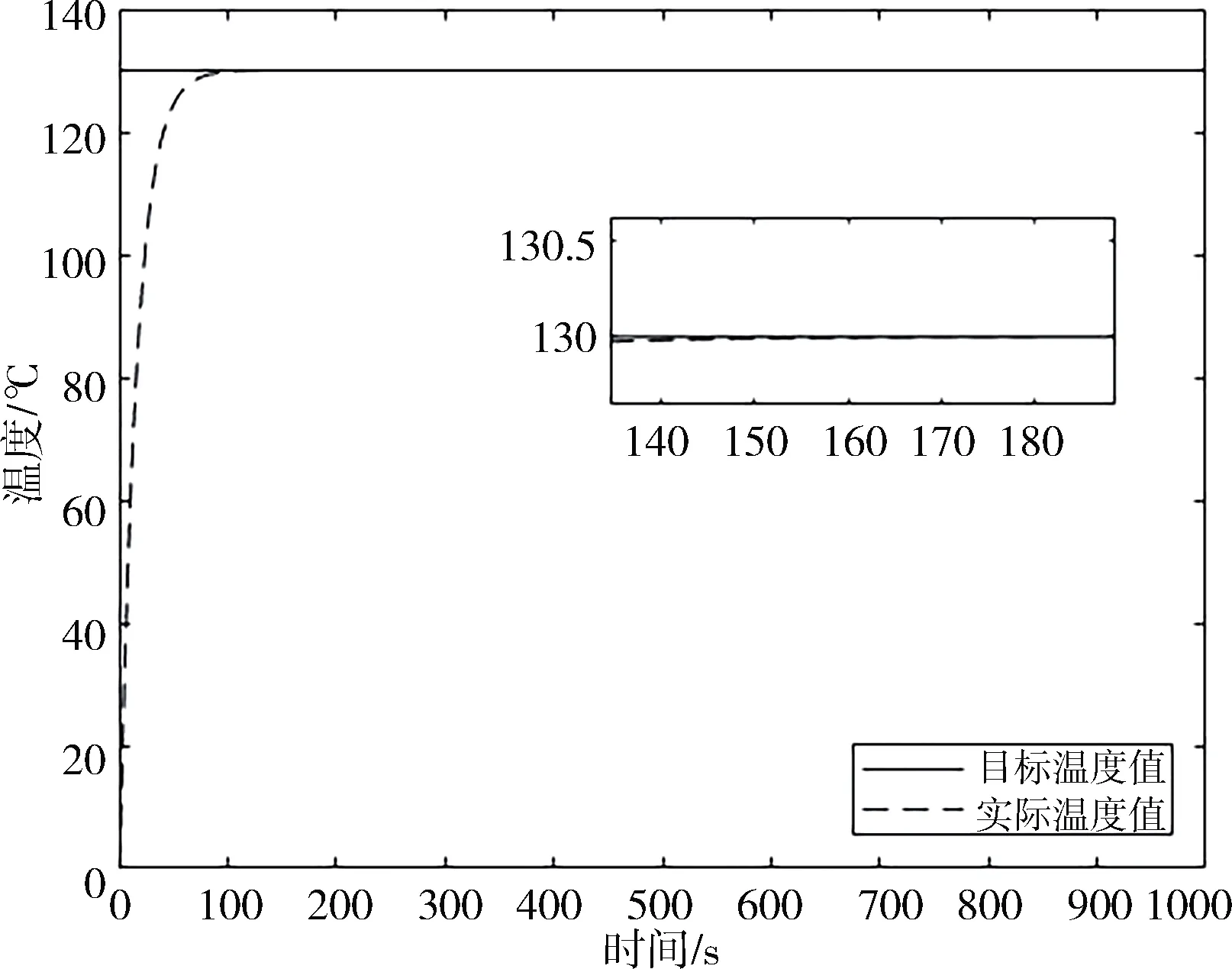
图5 仿真实验结果曲线

改进算法的适应度曲线如图6所示，我们可以看出，在种群数量为100的情况下，算法迭代7次就可以求解出最优结果.算法收敛速度快.

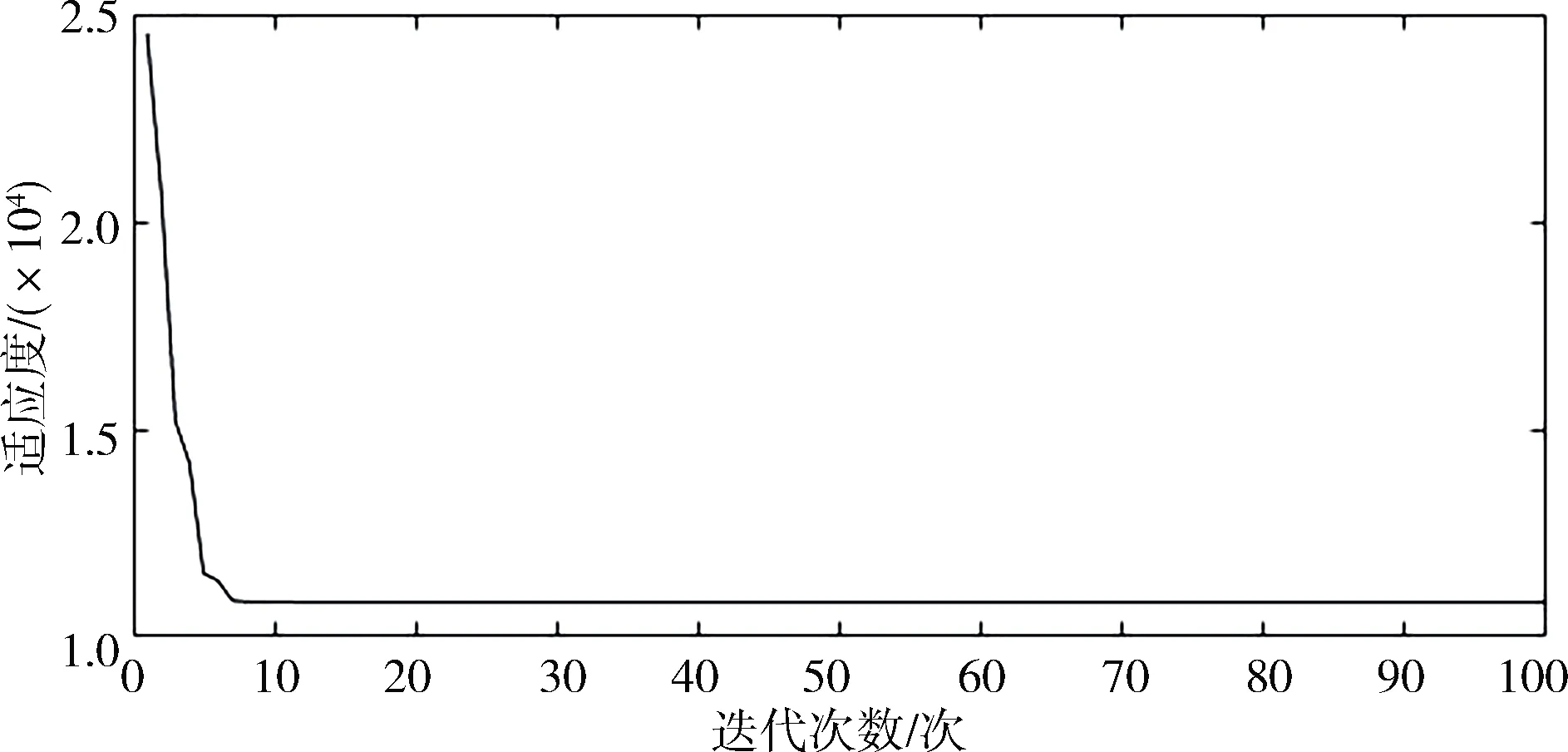
图6 适应度曲线

为了体现本算法的优势之处，我们将本算法的整定结果与PLC中PID自整定模块整定结果[5]、粒子群算法整定结果[7]以及基于模拟退火的改进粒子群算法(SACPSO算法)的整定结果[14]进行比较，同时对这4种算法的优化时间进行统计.4种算法求解结果如表1所示.通过表1我们可以看出，相对于继电反馈算法、粒子群算法以及基于模拟退火的改进粒子群算法，本文改进算法自整定时间最短(155 s)，有较大的优势.

表1 算法求解结果

我们将这4种算法所求参数分别进行仿真实验，仿真结果对比曲线如图7所示.根据结果我们可以看出，本文改进算法的超调量为0且达到目标温度所用时间最短；粒子群算法优化结果超调量最大且震荡严重；SACPSO算法优化效果相较于粒子群算法优化效果更好，达到稳定的时间与本文算法基本一致，但是超调量也较大；继电反馈算法优化结果超调量低,但是达到目标温度所需时间过长.因此本文算法相比于其他3种算法具有明显的优势.

图7 仿真结果对比曲线

5 现场实验

将仿真优化PID参数输入PLC控制器进行实验，通过网线将PLC与上位机连接后，进行通讯，每隔0.5 s采集一次温度数据，将采集的温度数据绘制成曲线图，结果如图8所示.

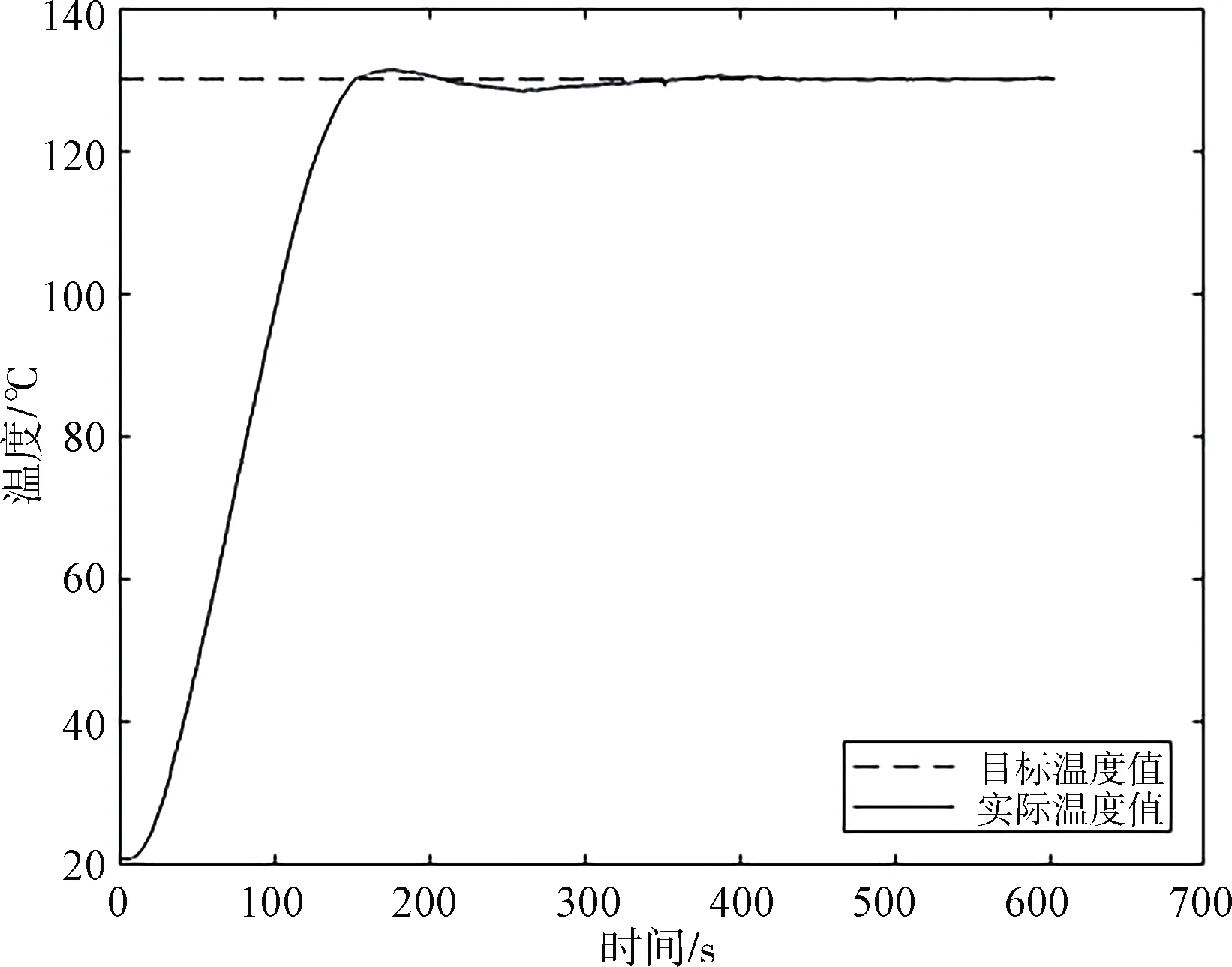
图8 温度实测数据曲线

从图8根据结果可以看出，实测曲线与仿真曲线有差别，可能由两个原因造成:(1)系统存在大的时滞性，仿真时未考虑;(2)系统实际的传递函数与MATLAB ident工具箱识别的传递函数有差异.但是温度实测曲线表明系统在140 s左右到达设定温度.在400 s之前温度有一定的偏差，偏差范围在[-1.8，+1.2]可以保证较好的热封质量;到400 s之后，温度趋于稳定，由于环境的波动会有微小的抖动.这时热封质量最佳.综上,本文算法优化的PID参数控制效果良好，可以满足TD150套袋机热封刀温度控制要求.

6 结 论

本文将鲸鱼算法和模拟退火算法结合并改进，再把改进后的算法在MATLAB R2017b软件上进行仿真对比实验.仿真对比实验结果表明，本文算法通过优化的参数在系统超调量以及稳定时间方面具有较大优势，且本文算法计算速度更快.我们将仿真所得优化参数进行现场实验，结果也表明了本文算法的可靠性以及优越性.综上，本文算法可以实现套袋机PID温度控制参数的自整定，提高温度的控制效果，保证封膜的质量，对套袋机热封刀温度控制有一定的实际意义.