GEO SAR中精确的面目标回波仿真方法
2022-07-22常法光李德鑫
常法光 李德鑫 董 臻
(国防科技大学电子科学学院,湖南长沙 410073)
1 引言
地球同步轨道合成孔径雷达(Geosynchronous synthetic aperture radar,GEO SAR)轨道高度是低轨SAR 的几十倍,具有驻留时间长、测绘带宽大及短重访周期等优点,在陆地测绘,地震、火山、泥石流、山体滑坡等自然灾害检测,全球碳、水循环研究,军事侦察,动目标指示等方面具有巨大的应用潜能[1-5]。近些年来,GEO SAR 吸引着众多国内外研究学者的注意,这使得GEO SAR 系统设计与成像处理等关键技术得到了快速发展。
由于目前尚无可用的GEO SAR 实测数据,关于GEO SAR 的成像研究都是基于仿真进行理论研究的。因此,GEO SAR 信号建模尤为重要,如何在回波仿真过程中维持保真度是研究的重点。文献[6]中提出一种维持回波保真度的改进GEO SAR 回波仿真方法,利用分布在弯曲地球表面的目标场景与卫星平台之间的几何关系,判断目标是否在波束覆盖范围内,进行回波的仿真。2014 年,文献[7]中考虑了在GEO SAR 合成孔径时间内由“停-走-停”在回波仿真中带来的误差,提出一种传播延迟等效模型,找到卫星的等效位置,提高了回波仿真的精度。对于有运动目标的场景也有部分学者进行研究,文献[8]中在考虑GEO SAR 复杂的轨道基础上给出了运动的舰船的回波仿真方法,并考虑了舰船的运动与旋转。综合上述研究成果,目前还没有一种能够全面考虑“停-走-停”误差以及精确判断位于弯曲地球表面的目标是否在波束覆盖范围内的回波仿真方法。并且GEO SAR 观测域很广,场景的构造的计算量很大,不利于基于回波仿真的后续工作展开[9]。同时,目前的成像算法都是以零高程的点目标作为研究对象,来验证算法有效性。然而在实际场景中,观测的目标都是起伏的复杂地形,现有的成像算法很有可能在实际地形中不再具有适用性。因此,一种精确且快速的面目标回波仿真方法很有价值。
基于现有回波仿真工作,本文提出一种贴合实际的面目标回波仿真方法。在场景构造中,利用插值来大大减少了观测场景的计算量。回波仿真过程中,结合轨道根数提出一种精确的接收信号时刻雷达位置计算方法,替代“停-走-停”模型,并且根据目标与雷达之间的几何夹角,准确判断目标是否在波束覆盖范围内。针对面目标场景内散射特性问题,本文给出了基于散射模型表达式与基于已经聚焦好的SAR 图像两种目标散射强度构造方法。最终,根据本文提出的方法进行回波仿真,结合成像算法验证了回波仿真的正确性。本文提出的回波仿真方法对于系统设计与成像算法验证等方面都很有研究意义。
2 回波仿真场景几何构造
在这一部分本文主要研究了面目标场景的构造以及如何在场景中加入高程信息。在面目标场景构造过程中,必须要分析清楚卫星与目标的几何关系,在选定好的坐标系下,得到目标场景在该坐标系下的三维坐标。在本文研究中,我们主要是在地心固连坐标系(the Earth-centered fixed CS,ECF,地固系)中定义场景坐标。其实地固系的定义与地惯系类似,不同之处在于X轴在地球赤道面内,指向格林尼治子午圈,而地惯系中的X轴在地球赤道面内,指向某一基准时刻的春分点。在卫星平台飞行轨道不同方位时刻,通过卫星与地球表面场景中目标的最近斜距,求出在地面上目标的坐标,然后,根据场景中目标的高程信息,利用几何关系就可以求出在地固系中场景内目标的三维坐标信息。
在GEO SAR 系统中,卫星的轨迹不再是线性的。为了更好的说明这一点,我们将卫星的星下点轨迹画了出来,如下图1所示。

图1 不同轨道倾角下星下点轨迹Fig.1 The sub-point trajectory under different inclination
由图1 可以看出,在GEO SAR 系统中,星下点轨迹是“8”字型轨道,且随着轨道倾角增加,观测区域所能覆盖的范围也就越大。此时卫星平台的位置以及速度不能再像低轨SAR 那样,用直线模型近似求解。根据系统的六个轨道根数(偏心率、半长轴、轨道倾角、升交点赤经、近地点幅角以及真近点角),参考目前已经成熟的航天器轨道基础理论,就可以在地惯系中得到卫星的位置与速度矢量,然后根据地球自转角速度常量(ωE=7.292115 ×10-5rad/s),可以将其转化为地固系下的位置和速度矢量[10-11]。至此可以得到轨道上卫星平台的位置和速度矢量随着时间的变化。下面对场景内目标的坐标求解进行描述。
可以将零多普勒中心时刻雷达波束中心视线与地面的交点作为场景中心点,根据卫星到目标的最短距离不同,在卫星轨道上不同位置处,求出所对应的目标坐标。根据以上分析,面目标场景中的每个点目标满足以下三个条件,参考公式(1),可求解出面目标场景内不同轨道位置处不同最短斜距直射点的目标坐标:(1)目标在地球椭球面上;(2)到卫星的最短斜距已知;(3)在卫星与目标斜距最短所对应的方位时刻,目标与卫星之间的位置矢量与卫星此时的速度矢量正交。然后在前后不同的方位时刻得到不同最短距离的点阵单元,最后就形成了位于地球表面上还没有加入高程信息的面目标场景。
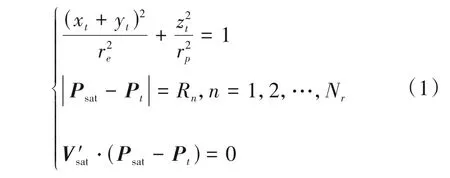
其中xt、yt、zt表示位于地球表面的点目标沿着各个轴的位置坐标,re、rp表示地球椭圆模型的赤道半径与极半径,其值大小分别为6378.137 km 和6356.909 km,Pt和Psat分别表示地表直射点的位置矢量以及与该点距离最近时的卫星位置坐标,Rn表示卫星与目标的不同最近距离,Nr表示场景距离向点数,Vsat表示与该点距离最近时刻卫星的速度矢量,(⋅)′表示转置。场景构造的示意图如下图2所示。
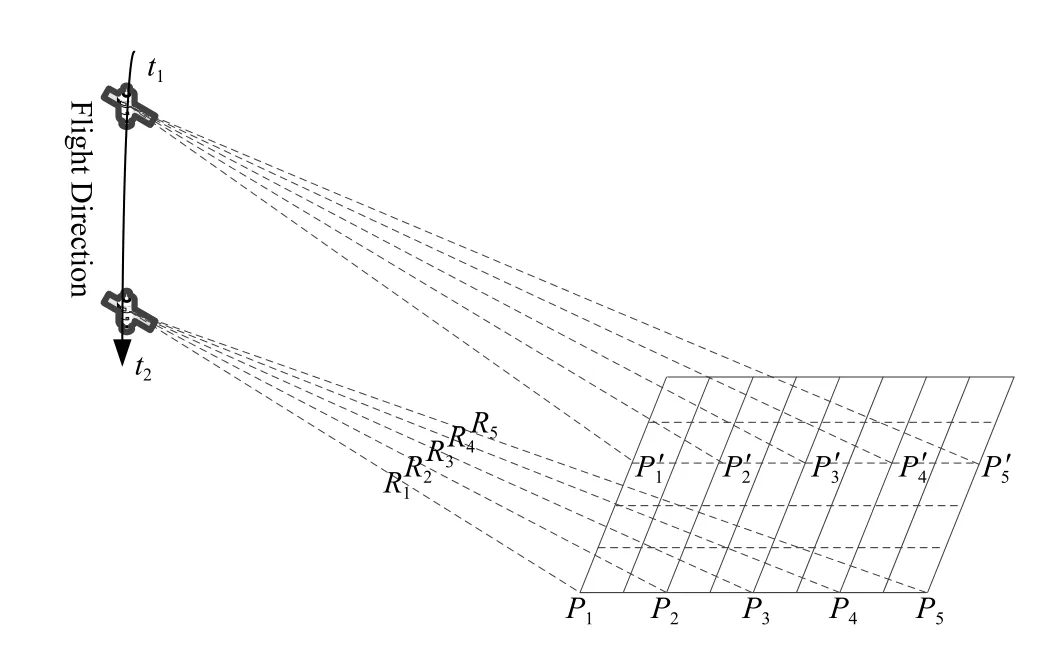
图2 场景构造几何示意图Fig.2 Scene construction geometry diagram
其中t1和t2表示卫星在不同的两个方位时刻,R1、R2、R3、R4和R5表示在t1(或者t2)时刻卫星与面目标场景中某个方位向各个距离单元P1、P2、P3、P4和的最短距离。
但是在面目标场景中,沿着距离向与方位向会有大量散射点,通过解方程组求解散射点坐标会产生很大的计算量,不能完成实时处理。因此本文就此问题提出一种改进方法,即只需通过求出几个离散等间隔的点,然后通过插值快速获得各个散射点目标,如公式(2)以及公式(3)所示。

其中c表示光速,fs表示采样率,R′n-R′n-1表示插值之前的距离间隔之差,Δnr表示沿着距离向采样的距离单元间隔数,ta,n-ta,n-1表示沿着方位向采样的方位时刻之差,Δna表示沿着方位向的采样时刻间隔,meshgrid(⋅)表示网格划分,XI,YI 表示插值前网格点,xi,yi 表示插值后网格点,Ppar,cor表示插值前网格点对应的某个轴目标坐标,interp2(⋅)表示二维插值,spline 表示数学中的三次样条插值,Pcor表示插值后网格点对应的某个轴目标坐标。下图3是完全根据解方程求出坐标以及通过插值得到的场景坐标,然后给出同一实验条件下的时间对比。其中,使用的参数如表1所示。

表1 系统参数Tab.1 System parameters
图3(a)就是在10 km×10 km 大小的场景内,布置了200×200 个点,完全由解方程得到的场景,图3(b)是通过解方程求出选择的20×20个点,图3(c)是对图3(b)沿着距离与方位向通过三次样条插值得到的200×200 点阵。可以看出,两种方式得到的场景是一致的。下面就两种方式在同一实验条件下的耗用时间进行对比,场景大小均为10 km×10 km,场景内散射点个数发生改变。

图3 场景三维坐标.(a)解方程得到的场景,(b)插值前得到的场景,(c)插值后得到的场景Fig.3 Scene 3D coordinates.(a)The scene obtained by solving the equation,(b)The scene obtained before interpolation,(c)The scene obtained after interpolation
由表2 可以看出,在场景内布置的散射点个数越多,直接用解方程求解位置坐标耗用时间越久,而提出的插值求解方法则可以很快的实现场景坐标的求解,包含获得插值前点阵以及插值处理后整体时间,相差也仅有零点几秒。以上的分析是对场景内没有高程信息的散射点的求解,在已知感兴趣区域的DEM 或者通过一个模型构造得到高程信息后,通过下式即可将高程信息添加进去。

表2 场景构造是否插值耗用时间对比Tab.2 Whether the scene is constructed with interpolation consumes tine comparison

其中Pt和h表示位于地球表面目标的坐标矢量和该位置处对应的高程,Pt,h则表示一定高程的目标坐标。|·|表示取模值。至此已经完成了场景的几何构造,得到了目标与卫星在地固系中的坐标,下面就可以精确的得出场景内每个散射点的回波,最后叠加起来即可。
3 回波信号模型
在这一部分根据已经构造好的场景进行回波仿真。基于已有的GEO SAR 回波仿真方法,本文着重考虑以下几个问题:信号发射与接收的双程斜距问题、波束覆盖问题与目标散射特性问题。
对第一个问题:就是“停-走-停”的问题是否要考虑。在GEO SAR 系统中由于轨道高度很高,导致信号发射到照射到目标的延时可达零点几秒,这种情况下传播时延导致的误差是必须考虑的[7]。因此,本文给出一种精确计算回波延时的方法。对于第二个问题:由于GEO SAR 观测域很大,在地面波束覆盖区域不再是矩形形状,沿着方位向将不同方位时刻的卫星和目标之间位置矢量与此时卫星速度矢量形成的角度对应的余角与天线的半波束宽度进行对比,当夹角小于半波束宽度时则表示目标在照射范围内,这样更能体现出回波仿真的精确性。对最后一个问题:目标散射强度的设置,可以分为两种方法,其一是通过不同材质类型的经验模型进行构造,根据目标场景是什么类型、材质,选定特定的散射模型进行构建,其二是选择一幅聚焦好的SAR 图像,以其幅度作为散射特性参数进行仿真。下面对这三个问题分别展开研究。
3.1 “停-走-停”时延问题
在GEO SAR 中,雷达与目标之间,从信号发射到接收的延时可达10-1数量级,此时在建立信号模型中必须将该时延考虑进去,否则会对斜距产生明显的影响[12]。文献[13]中提出利用发射时刻卫星与目标的斜距时延替代接收时刻卫星与目标的斜距时延,从而计算双程斜距信息,该方法称为“发射时延替代法”,本文结合卫星与目标之间的几何关系,如下图4所示,对目标与雷达之间的时延进行了更加精确的计算。
在图4 中,雷达在PS0位置处于t0时刻发射信号,经过时间Δt延时后,于t1时刻信号到达目标PT处,在此期间,雷达从PS0运动到PS1位置,此时信号从目标返回,经过一段时间后,于t2时刻到达雷达PS2处,于t3时刻,雷达到达PS3位置,其中t3与t1之间的时间间隔也为Δt。在不考虑“停-走-停”误差时,是假设从信号发射到接收,雷达一直位于PS0处,当假设发射时延与接收时延相同时,接收信号时雷达位于PS3处,但其实雷达在接收信号时位于PS2处。下面就如何找到从信号返回到接收的时延τ进行分析。

图4 信号传播几何关系Fig.4 Geometric model of signal propagation
当系统的六个轨道根数固定时,卫星在轨道上不同时刻的位置可以求出,因此,可得到关于时延τ的等式。

正如公式(5)所示,雷达从PS1到PS2的时延与从目标PT返回到PS2的时延相同,都为τ。根据此式,即可解出时延τ,从而可以用该方法准确计算出双程斜距信息。下面给出用该方法得到的准确双程斜距与“停-走-停”模型和“发射时延替代法”得到的斜距模型在合成孔径时间内的误差变化曲线,以及对应的相位误差变化曲线。误差计算公式如下:
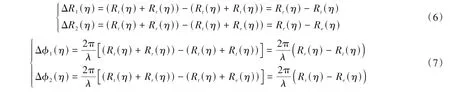
其中η表示方位时间,Rt表示信号发射时雷达与目标之间的距离;Rr表示雷达接收信号时,雷达与目标之间的距离;Re表示认为接收时延与发射时延相同,此时的雷达位置与目标之间的距离,λ表示信号波长。
由图5 可以看出,采用“停-走-停”模型在所给位置处合成孔径时间内,最大斜距误差可达3 m 左右,对应的相位误差很大,会严重造成回波仿真的失真;当用“发射时延替代模型”得到的雷达接收信号位置,与通过解方程求出的雷达准确位置相比,在真近点角为0°时最大相位误差超过π/4,在真近点角为90°时最大相位误差控制在π/4以内。因此,在回波仿真过程中,通过解方程的方式可以准确找到雷达接收信号的位置,在轨道上卫星与目标之间斜距变化不是很剧烈的位置,为了提高计算速度,用“发射时延替代模型”也可以在可忽略误差范围内,得到雷达接收信号的位置。本文接下来的分析中,回波仿真中采用解方程得到雷达接收信号的位置,并且用R(η)表示二分之一双程斜距,即:
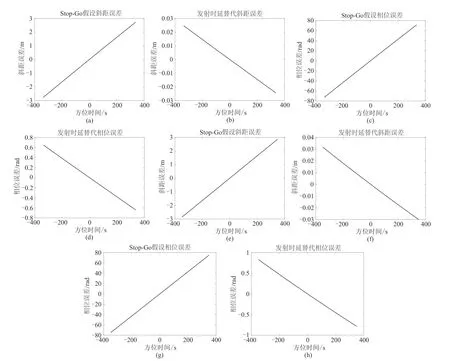
图5 “停-走-停”模型与“发射时延替代模型”对应的斜距与相位误差.(a)~(d)真近点角为90°,(e)~(h)真近点角为0°Fig.5 The slant range and phase error corresponding to the stop-go model and transmission delay replacement model.(a)~(d)True anomaly is 90°,(e)~(h)True anomaly is 0°
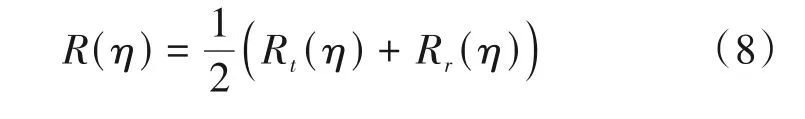
3.2 波束覆盖问题
在传统回波仿真方法中,由于低轨SAR 观测区域较小,场景模型位于平坦的地球表面上并且波束在地面的投影近似为矩形。然而在自然条件下,卫星所观察到的场景是位于地球表面上的曲面,并且在GEO SAR 中波束在地面上的投影近似为椭圆。在低轨情况下,近似引起的误差在回波仿真中可忽略,而GEO SAR 中由于波束覆盖区很大,将会在回波仿真中引起很大的误差。并且矩形区域的近似会影响目标的积累时间,这将对方位分辨率产生影响[6]。因此,为了精确地仿真回波,在本文提出一种准确判断目标是否被波束覆盖的方法。
在距离向,与低轨SAR 一样,通过窗函数判断回波是否在脉冲持续时间内。在方位向本文提出的窗函数是通过判断卫星速度方向与卫星-目标方向形成角度的余角和波束半宽度的大小,进而判断目标是否在波束覆盖范围内。如公式(9)所示。

其中La表示天线方位长度,θa表示天线方位向波束宽度,Psat、Pt和Vsat分别表示地固系下卫星位置矢量、目标位置矢量以及卫星的速度,∠表示两个矢量之间的夹角,tr表示距离向(快)时间,|·|表示绝对值,Tr表示脉冲持续时间,Wa和Wr分别表示方位与距离窗函数。通过这样处理,即可准确的判断目标是否在波束覆盖范围内。
3.3 散射特性问题
一般来说,目标的RCS 散射强度参数仿真是基于一个随机粗糙表面的散射模型表达式和电磁波投影理论[14]。当然这种散射系数的计算方式一般为经验公式,对于每种类型的材质都会有不同的经验公式。因此,在回波仿真中,往往计算起来比较麻烦。在本文中,我们还可以将一幅已经聚焦好的SAR 图像作为参考,用图像中的幅度取代传统的散射系数计算方法,当然还可以加入原始图像中的相位信息。
根据以上的分析,可以精确的得到窗函数、散射强度以及斜距,则可精确的实现GEO SAR 系统中回波仿真。
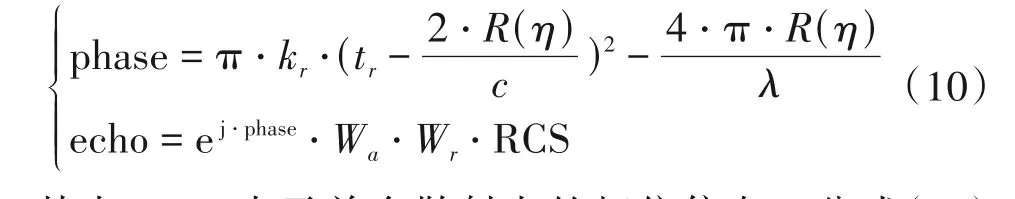
其中phase 表示单个散射点的相位信息。公式(10)即为单个散射点回波的表达形式,将每个点的回波叠加之后就可以得到场景的回波。在下一小节中,我们分别用散射模型表达式和原始SAR 图像作为散射强度的输入,进行回波仿真。
4 仿真实验分析
4.1 仿真数据分析
根据之前的理论分析仿真回波并通过成像验证所提出方法的正确性。在这一小节,我们通过已知的散射模型作为RCS 散射强度输入,进行回波仿真。系统所有参数可参考表1。
要产生SAR 信号仿真中的RCS矩阵,使用佐治亚工学院Currie等人提出的陆地散射特性经验模型来计算,这个方法计算较为简单,但缺点是没有相位信息。因此,在此次仿真中,使用Currie的方法来产生RCS 幅度,然后对这个幅度矩阵添加一个在(-π,+π]之间均匀分布的随机相位,然后把相位添加进去[15]。该模型表达式为:

其中θ是小平面单元的入射角;σ是设计场景表面高度起伏的标准差;A=0.0096、B=0.83、C=0.0013、D=2.3 是由经验获得的常数,在不同场景中,如:田地、草地、庄稼地、树林、砂土、岩石、城市区和被雪覆盖的地面,这几个参数是不一样的,而本文给出这四个参数的数值就是田地和砂土所对应的经验参数。σ0即是我们想要得到的RCS矩阵。图6是设置的圆锥场景以及根据公式(11)得到的场景散射强度图。

图6 圆锥以及根据模型得到的散射强度.(a)圆锥,(b)散射强度Fig.6 The cone and the scattering intensity from the model.(a)Cone,(b)Scattering intensity
下图7 为地固系中设置的圆锥,然后按照上述分析过程进行回波仿真,并用改进RD-ACS 算法[16]成像得到的结果。

图7 地固系中圆锥以及成像结果.(a)地固系中圆锥,(b)成像结果Fig.7 The cone in ECF and the imaging result.(a)The cone in ECF,(b)The imaging result
在布置的场景中我们给圆锥设置了一定高度,为了验证在回波中加入了高程信息,可以借鉴于干涉SAR 的处理。我们同样将图6(b)所示的散射强度作为RCS 矩阵的输入,依次布置三个场景:(1)将圆锥布置在一个斜面上;(2)只有斜面的场景;(3)场景为地表的平面,其中斜面如下图8所示。
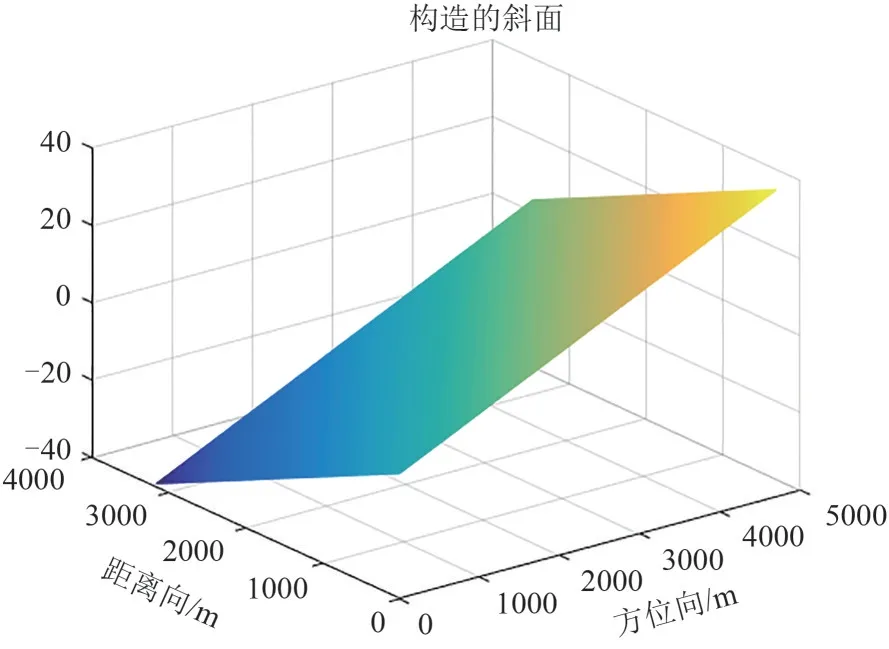
图8 斜面Fig.8 The slope
根据上述三种场景可得到每个散射点的位置坐标,按照之前分析进行回波仿真,并用改进RDCS 算法进行成像,最后将三组成像结果进行干涉,即取出相位进行共轭相乘。结合布置的场景以及干涉的相关知识可知:场景(1)与场景(2)的干涉结果会有圆锥状的条纹;场景(1)与场景(3)的干涉结果会有线状条纹以及圆锥状的条纹;场景(2)与场景(3)的干涉结果会有线状条纹。这些条纹的主线是与场景的地形高程有关的。下图9为三种场景的干涉结果。
由图9 可以看出,最终的干涉结果与之前的分析是一致的。

图9 依次为场景(1)与(2)、场景(1)与(3)、场景(2)与(3)的干涉结果Fig.9 The interference results of scene(1)and(2),scene(1)and(3),and scene(2)and(3)
4.2 实测数据分析
本小节利用一幅已经聚焦好的SAR 图像,进行回波仿真。这里选择的是“高分三号”聚焦图像,如下图10所示。

图10 整幅场景以及选择出的感兴趣区域Fig.10 The entire scene and selected interested region
从整幅场景中选择了一条特征清晰的小路,并将这部分给放大处理,以此作为RCS 矩阵的输入,并按照上述流程进行回波仿真,最后用常规的CS算法和改进RD-ACS 算法进行成像,成像结果如图11所示。
由图11可知,通过对选择出的小块区域按照本章的流程进行回波仿真,用改进RD-ACS 算法进行成像,与原始图像相比可以得到很好的效果,而用经典的CS 算法进行成像,聚焦效果很差,这是由于空变引起的散焦,而改进RD-ACS 算法可以补偿掉空变误差,详细介绍可参考文献[16]。

图11 成像结果.(a)CS算法,(b)改进RD-ACS算法Fig.11 The imaging results.(a)The CS algorithm,(b)The improved RD-ACS algorithm
5 结论
本文主要研究了GEO SAR 系统中面目标的回波仿真方法,由于GEO SAR 合成孔径时间很长、观测区域很广,会造成很大的数据量,在时域回波仿真中给计算带来很大的负载。因此,我们提出一种快速的面目标场景构造方法,通过插值实现场景的快速布置,在这一环节大大减小了计算量。与此同时,还重点研究了“停-走-停”效应、波束覆盖问题以及散射强度相关问题。在回波仿真中,充分考虑GEO SAR 中椭圆型轨道以及长合成孔径时间带来的发射-接收时延问题;从实际情况出发,在弯曲的地球表面中严格根据卫星速度方向与卫星-目标方向之间形成角度的余角和半波束宽度去判断目标是否在波束覆盖范围内;对于RCS 散射强度问题,给出了散射模型与已经聚焦好的SAR 图像两种方式作为RCS 矩阵,实现回波仿真。最后,分别以仿真数据以及实测数据,根据提出的流程进行回波仿真,然后用可在GEO SAR 中补偿空变误差的改进RD-ACS 算法进行成像,验证回波仿真的正确性。这部分工作对于整个GEO SAR 系统设计以及后续成像算法研究都很有帮助。
