基于极限学习机的低频雷达自适应测高技术
2022-07-22朱伟徐晋贺芃
朱 伟 徐 晋 贺 芃
(中国电子科技集团公司第三十八研究所 合肥 230088)
0 引言
低频段雷达波长较长,具有探测距离远、反隐身能力强等特点,同时由于其波束宽,在俯仰上波束打地、地面反射强,造成目标回波的“多径”现象严重。目标的直达波和多径反射波信号具有强相关性,低仰角时直达波和多径反射波位于一个波束宽度之内,同时波瓣分裂会引起接收信号的电平闪烁,信噪比波动较大,导致测高精度低。
目前传统的低仰角测高方法主要集中于利用阵列信号处理技术。文献[1]建立多相干源情况下的信号模型,提出广义最大似然算法;文献[2]建立精确多径模型,分析了反射面高度对测角性能的影响,提出合成导向矢量地形匹配最大似然算法;文献[3]提出将压缩感知思想加入阵列信号处理技术,提出基于稀疏估计的测高方法。阵列信号处理技术需要对直达波和多径信号进行数学建模,模型中包含的参数包括:工作频率、布阵形式、直达波角度、地面反射系数、阵元回波波程、反射波能量分布、反射波角度分布等,由于实际地面反射环境复杂,影响测量精度的变量太多以至于难以建立精确的多径信号数学模型,通常将雷达反射面做近似处理,会带来一定的误差。
在传统阵列信号处理算法以外,计算智能算法也被引入该领域中。文献[5]将径向基函数神经网络应用于米波雷达测高,在简单的多径模型下验证径向基函数非线性波束形成测高方法的有效性;文献[6]将神经网络思想应用于米波雷达测高,但如果估计值不在训练值范围内,测高精度将大大下降,所以要全面考虑训练样本数据的各种可能情况来提高测高精度。以上这些计算智能方法使用的是后馈神经网络,其参数多且复杂,训练极为耗时,学习效率太低,容易收敛进入局部最小值。
极限学习机(Extreme Learning Machine,ELM)是一种简单有效的前馈神经网络学习算法,输入层到隐层之间的连接权重和隐层的偏置都是随机确定,通过广义逆变换计算得到隐层到输出层之间的连接权重.ELM 具有快速的学习能力和良好的泛化能力,广泛应用于分类和回归等问题中。为了解决低频段雷达在复杂多径环境下的高精度测高问题,将极限学习机应用于雷达低仰角测高场景,提出一种阵地自适应、智能自学习、无需阵地反射面模型等的测高方法。
1 极限学习机的理论模型
极限学习机由一个输入层,一个隐含层,以及一个输出层构成,网络结构如图1所示。
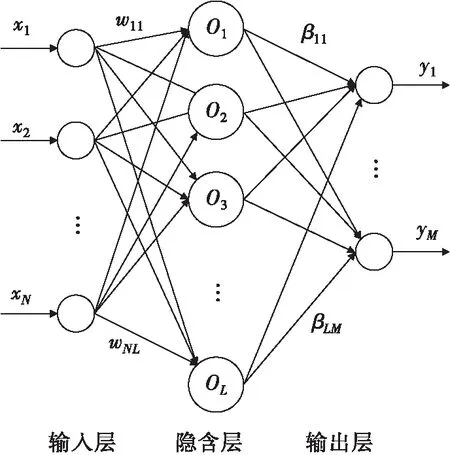
图1 极限学习机网络结构
图1中,~为个输入,~为个神经元,~为输入层与隐含层的连接权值,~为隐含层与输出层的连接权值,~为个输出。
对于给定的个训练样本(,),其中=[1,2,…,]∈,=[1,2,…,]∈,标准的单隐层前馈神经网络在个隐含层节点的情况下的数学模型被描述如下

(1)
其中=[1,2,…,]是连接第个隐含层结点和输入结点的权重向量,=[1,2,…,]是连接第个隐含层结点和输出结点的权重向量,是第个隐含层结点的门限,是第个输入变量,()是单隐层网络的非线性传递函数,等式(1)可简写为如式(2)形式。
=
(2)
其中为隐含结点的输出矩阵。

(3)
=[,,…,]是输出层的权值向量,=[,,…,]是样本的输出矩阵。
输出层的权值可以通过最小化平方误差求出为
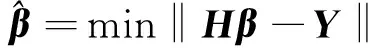
(4)
其中=[,,…,]是目标矩阵,如果隐含层的权值和偏置可以在不考虑输入数据的情况下随机分配,且矩阵的秩为。输出层的权值可以通过寻找线性模型的最小范数最小二乘解的方法求出为

(5)
其中为的矩阵的摩尔广义逆。
极限学习机的隐含层参数不需要手动调节,其中,参数包含输入权值和隐含层偏置都可以被自动随机生成,使用中仅仅需要根据隐含层输出矩阵的求逆得到输出权值,相比传统的后馈神经网络算法,极限学习机学习结构简单和学习速度快。
2 基于极限学习机的低频雷达自适应测高算法
雷达均配备有ADS-B(Automatic Dependent Surveillance - Broadcast,广播式自动相关监视)设备或SSR(Secondary Surveillance Radar,二次雷达),可以获取民航目标或其它合作目标的真实位置,使得雷达同时可以得到目标的回波数据和目标的真实仰角、高度。因此,可以建立极限学习机的预测模型,利用合作目标的回波数据和真实仰角对极限学习机进行训练。从而,对非合作目标的仰角测量可以利用训练的极限学习机对目标仰角进行预测。
本文算法步骤如下:
1)步骤1:根据方位、距离对雷达覆盖范围进行区域划分。
雷达反射面主要与目标所在的距离、方位有关,将雷达覆盖范围按照方位、距离进行区域划分,如图2所示。方位、距离以等间隔方式均匀划分,根据阵地环境及实际航线轨迹,可将单个区域或若干区域使用同一极限学习机进行训练和预测,如图2中阴影所示,两个极限学习机分别覆盖不同大小的划分区域。
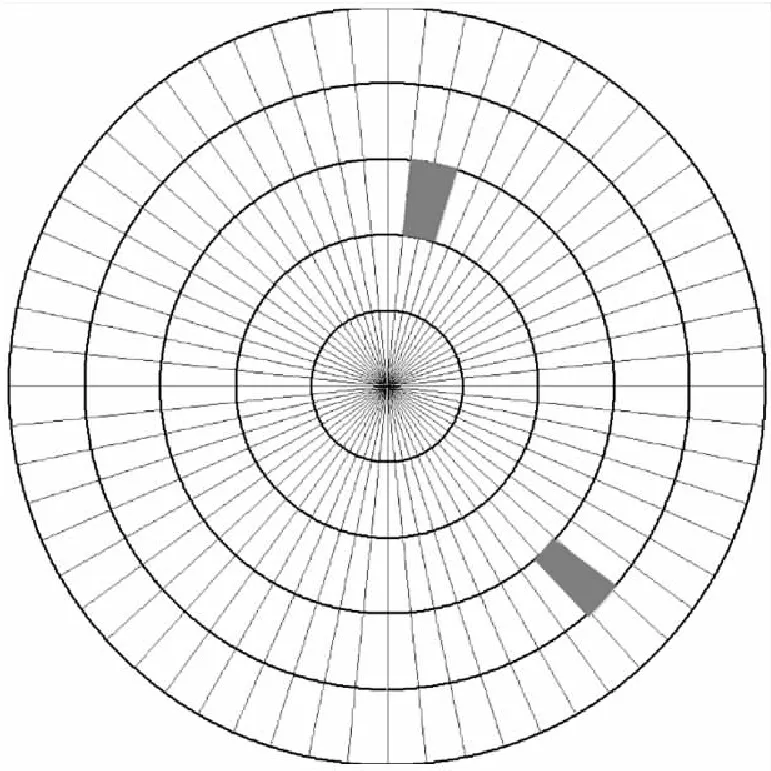
图2 区域划分示意图
2)步骤2:从雷达回波中提取目标信号。
阵列为一垂直放置的均匀线阵。均匀线阵由个阵元组成,阵元间隔。对雷达回波信号进行脉冲压缩、杂波对消和恒虚警检测等处理后,得到回波信号()为
()=()+()
(6)
其中,()为×1维的阵元接收数据;()为×1维的白噪声,满足零均值、方差为的复高斯分布,各阵元输出噪声统计独立;()为信号矢量;为阵列流型
=()+
(7)
其中,()为直达波的导向矢量;为目标的直达波角度;()=exp(-j2πsin()·[0,1,…,-1]),上标T表示矩阵转置,为入射信号的波长,为多径信号的导向矢量,难以用数学模型进行精确描述。
3)步骤3:获取目标的空间谱特征,对特征数据进行归一化。
对目标信号进行傅里叶变换获得目标的空间谱,为了保证空间谱采样率,傅里叶变换的点数可选择256点或更高。考虑到目标信号有强弱不同,避免数据因为相差较大而造成的误差,对目标空间谱进行归一化。
目标归一化特征信号()为
()=mapminmax[FFT((),)]
(8)
其中,mapminmax表示最大最小归一化;FFT表示傅里叶变换;表示傅里叶点数。
4)步骤4:判断目标是否为合作目标,如果是合作目标则进行步骤5,如果不是合作目标则进入步骤6。
如果目标为合作目标,通过SSR或ADS-B可以获得目标的经纬高信息,通过坐标转换可得到目标相对雷达的俯仰角和高度。
5)步骤5:利用合作目标数据来训练极限学习机。
将目标特征和合作目标的仰角值加入训练数据库,利用训练数据库来训练极限学习机,送出合作目标的仰角值和高度值。
6)步骤6:判断目标所处的极限学习机是否训练充分,如果训练充分则进行步骤7,如果没有训练充分则进入步骤8。
7)步骤7:利用极限学习机对目标仰角进行预测。
将目标的归一化空间谱特征作为测试数据,通过已完成训练的极限学习机进行预测,极限学习机的输出值为目标仰角,再通过三角变换得到目标高度。
8)步骤8:利用阵列超分辨技术进行测角。
如果没有合作目标且目标所处的极限学习机未训练充分,则利用阵列超分辨技术对目标仰角进行估计,再通过三角变换得到目标高度。
算法流程如图3所示。
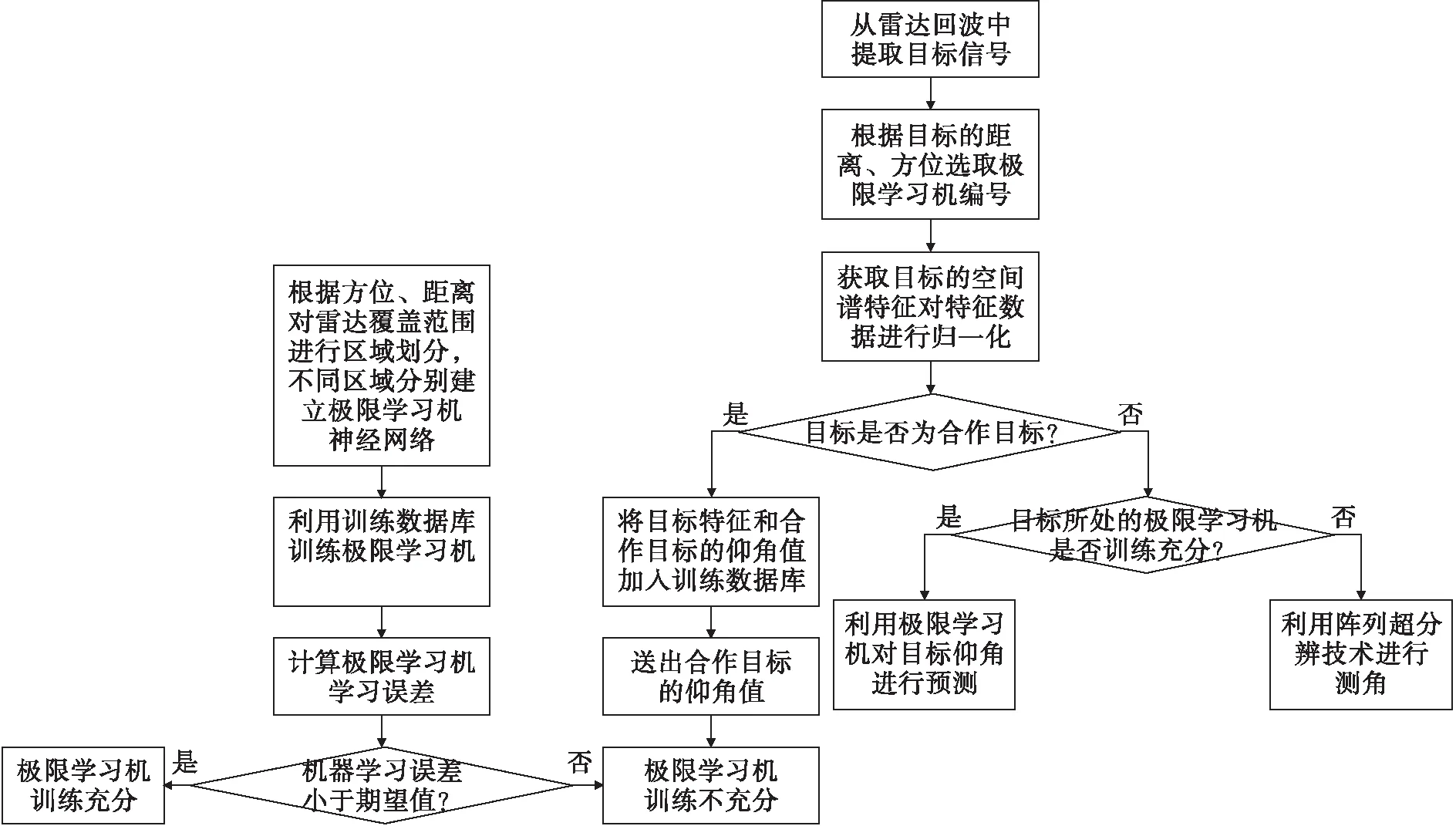
图3 算法流程图
3 实测数据效果
将本文算法应用到某低频段雷达中,雷达的俯仰波束宽度约7°,目标仰角位于在一个波束宽度以下时多径现象严重。选取若干航线上的23批目标,航线如图4折线所示,选取三个区域分别建立极限学习机,三个区域目标均在低仰角区,区域如图4深色扇形所示,三个区域分别为:

图4 目标航线图及区域选择
1)方位:306°~312°;距离:140km~160km;
2)方位:330°~336°;距离:100km~120km;
3)方位:54°~60°;距离:130km~150km。
极限学习机隐含层神经元激活函数为logsin函数。区域1目标仰角区间为2.2°~4.5°,使用的训练样本为518个,测试样本为129个,通过训练后的极限学习机对测试样本预测的结果如图5(a)所示,经统计,预测值的均方根误差为0.098°,高度均方根误差为255.8m;区域2目标仰角区间为3.3°~6°,使用的训练样本为434个,测试样本为109个,通过训练后的极限学习机对测试样本预测的结果
如图5(b)所示,经统计,预测值的均方根误差为0.094°,高度均方根误差为179.5m;区域3目标仰角区间为2.7°~4.7°,使用的训练样本为668个,测试样本为167个,通过训练后的极限学习机对测试样本预测的结果如图5(c)所示,经统计,预测值的均方根误差为0.083°,高度均方根误差为202.1m。从图5可以得出,在极限学习机训练充分的情况下,能够有效地估计多径环境下的目标仰角,并能达到较高的测角和测高精度。
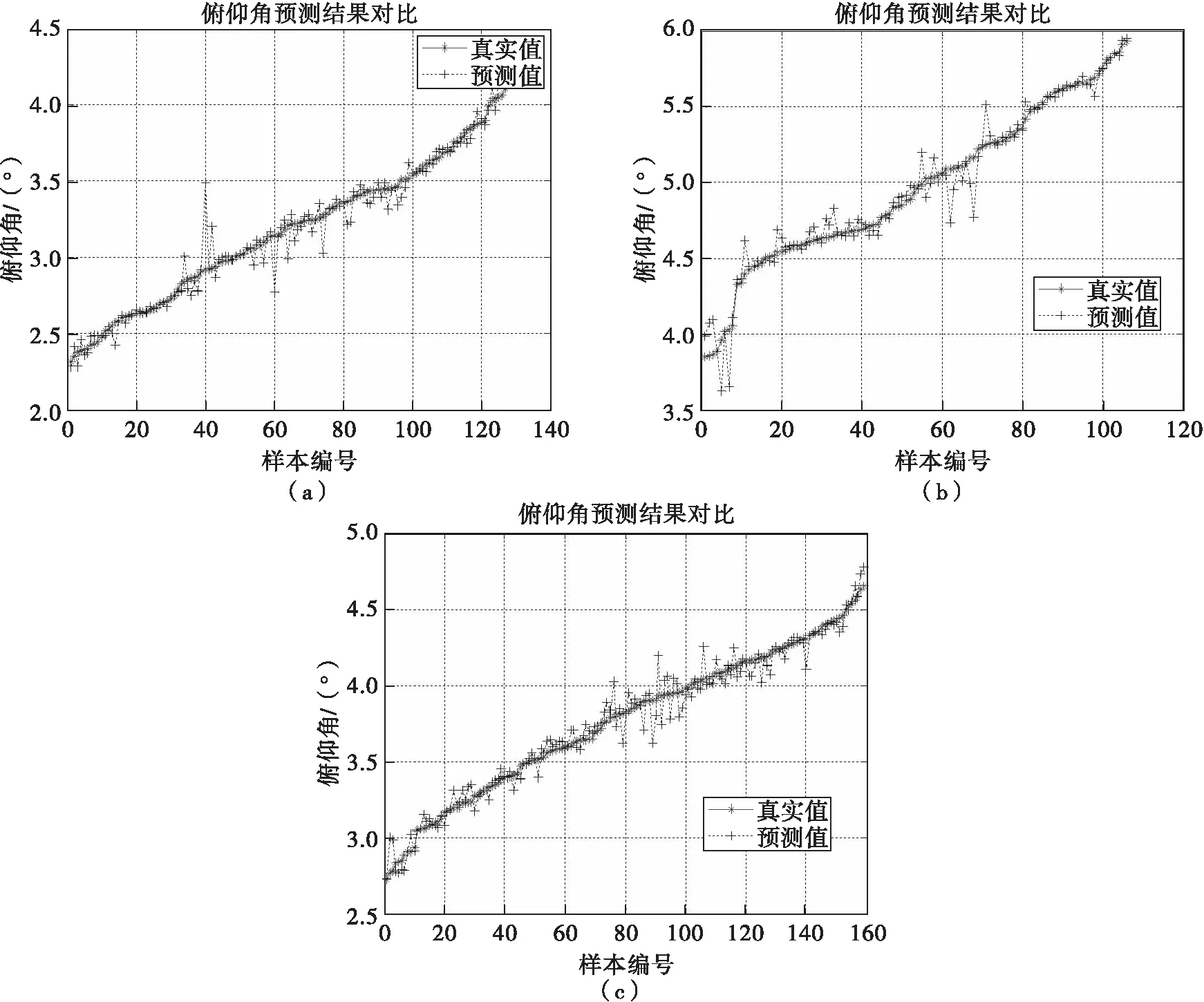
图5 实测数据结果图
4 结束语
利用合作目标的回波数据和真实仰角对极限学习机进行训练,对非合作目标的仰角测量利用训练的极限学习机对目标仰角进行预测。雷达工作时间越长,获取的训练样本越多,极限学习机预测结果越准确。该方法不需要雷达反射面的任何参数,具有良好的鲁棒性、泛化性和准确率。基于极限学习机的低频段雷达测高技术能够准确、可靠、智能地实现复杂多径环境下低频段雷达的高精度测高,通过实测数据处理结果进行了验证。
