Prophet 混合模型应用于基站网络流量长期预测

张家晨，左兴权，黄 海，韩 静，张百胜

1.北京邮电大学 计算机学院（国家示范性软件学院），北京 100876

2.中兴通信股份有限公司，上海 201203

随着5G网络以及移动端设备的逐渐普及，人们对于移动数据流量的需求不断增加。随之而来的数据流量将会以指数形式增长，对于网络运营商而言，提供不受阻碍、无处不在的高质量服务意义重大。其中，如何建立准确的长周期预测基站小区网络流量的模型，以指导运营商扩容基站小区无线设备将是一个挑战。

基站小区网络流量通常以时间序列的形式呈现，预测周期可分为短周期时间序列预测（预测时长按分钟、小时和天）和长周期时间序列预测（预测时长按天、周和月）。短周期的基站小区网络流量预测相对成熟，主要包括三类方法，即传统统计模型建模方法、神经网络顸测方法、基于序列分解结合以上两种方法的混合模型方法。

传统统计模型建模方法主要包括自回归模型（autoregressive model，AR）[1]、滑动平均模型（moving average model，MA）[2]、回归滑动平均模型（autoregressive moving average model，ARMA）[3]、差分整合移动平均自回归模型（autoregressive integrated moving average model，ARIMA）[4]等模型及其改进。文献[5]使用线性回归和非线性回归方法，对4G基站流量进行预测，实验结果表明非线性预测算法性能优于线性机器学习算法对基站流量进行直接建模。文献[6]使用自回归滑动平均模型与三指数平滑模型，预测上传和下载热点的流量，结果表明三指数平滑模型具有更好的预测性能。文献[7]提出了基于SARIMA（seasonal auto regressive integrated moving average）模型对网络流量进行预测，实验表明当预测步长小于10时，预测精度更高。

用于网络流量预测的神经网络模型包括循环神经网络（recurrent neural network，RNN）[8]、BP神经网络（back propagation neural network，BPNN）[9]及其变体[10]。文献[11]利用RNN为网络流量建立预测模型，可准确预测各种网络应用场景下的流量变化趋势。文献[12]利用萤火虫群算法优化BP神经网络，对网络流量进行预测，仿真结果表明该算法具有较高的预测精度。

当前，以“分解和集成”方法为基础的混合模型预测方法在网络流量预测中表现良好。文献[13]提出基于EEMD与RBF神经网络组合模型对网络流量进行预测。文献[14]为了解决自相似网络流量预测，提出了集合EMD和ARMA的组合模型。文献[15]基于小波分解联合使用长短期记忆网络（long short-term memory，LSTM）模型，该组合预测模型在预测流量突发性方面的性能优于普通的LSTM网络模型。文献[16]提出了一种基于小波变换和SARIMA模型的方法，该方法比单一预测模型具有更高的预测精度。文献[17]提出基于经验模态分解（empirical mode decomposition，EMD）和支持向量机（support vector machine，SVM）模型对网络流量进行预测，比单独使用SVM模型具有较高的准确度。文献[18]提出小波分解联合BP神经网络的方法对网络流量进行预测，通过使用一种自适应学习率的方法对BP进行优化以提高预测准确度。

可以看出，以上研究大多对基站网络流量进行短期预测，缺乏长期预测研究，而只有对基站网络流量进行长期预测，才能更有效地指导基站的扩容。此外，基站网络流量数据存在较大的噪声以及数据缺失现象，当前方法普遍未全面考虑这些情况，导致难以保证实际预测效果。

本文提出了一种结合EEMD与Prophet模型的基站小区网络流量长期预测方法（E-Prophet）。EEMD是对EMD分解方法的一种改进，解决了EMD因极值点分布不均匀导致的“模式混合”现象，通过EEMD分解能够对信号进行平稳化处理，将时间序列分解为具有不同时间尺度的分量序列。相比小波分解，EEMD不依赖基函数且具有很好的自适应性。Prophet模型[19]能把时间序列分解成不同的成分，其中趋势项成分对于具有长期趋势性的时间序列预测具有较好的效果，季节项成分对于具有周期性（年、月和星期）的时间序列具有较好的效果。Prophet模型已经应用于时间序列预测领域，例如，2019新冠肺炎的分析和预测[20]，以及对LTE（long time evolution）小区流量增长和拥塞预测[21]等。通过观察，发现基站小区网络流量数据具有一定周期性，与此同时由于小波分解采用不同的小波基和分解层数对结果影响很大，而且分解效果不如EMD[22]理想，因此本文提出基于EMD/EEMD分解结合Prophet模型对基站小区网络流量进行预测，其主要过程包括两步：首先通过EMD/EEMD分解模型对基站小区网络流量进行分解；其次使用Prophet模型对各个分量进行预测，并累加求和各个分量最终预测值得出预测结果。结合EEMD对网络流量良好的分解特性，以及Prohpet模型对各分量时间序列准确的预测特性，E-Prophet方法能更好地适应于基站小区网络流量的长期预测。

本文的主要贡献为引入Prophet模型到小区流量预测，Prophet模型虽然已被应用于多种时间序列预测中，但还没有研究将Prophet用于基站小区网络流量预测。通过真实数据的实验证明E-Prophet比其他传统模型具有更好的预测效果。

1 基站小区网络流量的长周期序列特性

Paxson和Floyd的研究发现[23]，小时级以上粗时间粒度的流量行为由于主要受外界因素的影响，不具有自相似性，而是一种非线性复杂的过程。本文研究的基站小区网络流量数据是按天统计，每天的流量数据为自忙时的流量，所谓自忙时是指当天流量最大的整点时刻。因此基站小区流量是以小时粒度采集，具有非线性特点，而且有时候因为设备或者人为因素，网络流量在采集过程中可能出现部分缺失值，这也为基站小区网络流量长期预测带来很大挑战。同时，用户在使用网络服务过程中受外界因素影响，网络行为具有一定的规律性和偶然性，因而产生的非线性宏观网络流量具有一定的周期性、突发性和偶然性。根据基站小区网络流量这些特性，网络流量X(t)可分解为趋势部分A(t)、周期部分P(t)、突发部分B(t)和随机部分R(t),如式（1）所示[24]：

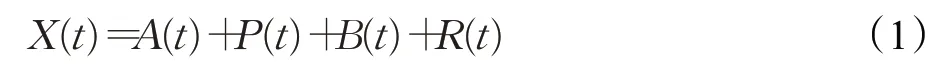
Prophet是一个类似GAM（generative additive model）的时间序列模型，模型本身采用加法模型，分别由趋势项拟合函数、季节项拟合函数、节假日拟合函数和随机项组成，非常适合具有上述分布特点的网络流量进行长期预测，具体表现为：Prophet模型趋势项和季节项能够分别拟合网络流量非周期性和周期性的长期变化规律；Prophet模型节假日项能够对因特殊节日而导致的有规律的网络流量暴跌或暴增进行拟合；同时如果数据中存在部分缺失片段，传统自回归模型如ARIMA则需要人为插入缺失值后才能进行预测，而Prophet能够根据已有的数据进行拟合，忽略缺失值对模型预测带来的影响。此外，通过EEMD分解后的流量序列成分较简单，使用Prophet模型后能达到更好的预测效果。

2 预测流程及方法

2.1 E-Prophet预测流程

基于E-Prophet预测流程方法如图1所示。首先，对每个基站原始小区网络流量进行EEMD分解；然后，对各个分量使用Prophet模型进行预测；最后，再对各个分量预测结果进行求和，得到该基站小区网络流量的最终预测结果。

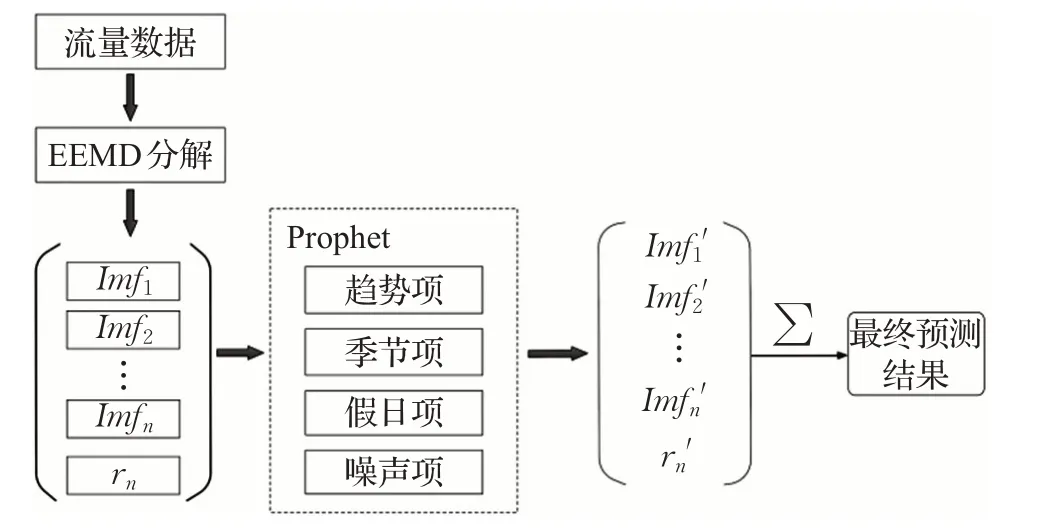
图1 E-Prophet的网络流量预测流程Fig.1 Network traffic forecasting process of E-Prophet

2.2 EMD和EEMD分解

经验模态分解（EMD）[25]是一种数据处理方法，用于处理非线性和非平稳数据。EMD通过希尔伯特变换将非线性和非平稳时间序列分解为分量子序列，包括多个IMF分量和一个残差项，而无需任何基函数或滤波函数。

IMF分量需满足两个判定条件：第一，在整个数据序列中，极值点的数量与过零点的数量相等或最多相差一个，所谓过零点是曲线经过纵坐标等于零的点。第二，在任一时间点上，由局部极大值点确定的极大值包络线，和由局部极小值点确定的极小值包络线的均值为零，即信号需满足对时间轴的局部对称性。EMD的步骤如下[26]：

（1）令{x(t)∈X:t=1,2,…,N}表示基站小区网络流量训练集时间序列，其中t表示天数。根据时间序列确定所有局部极值，并将所有的极大值和极小值通过三次样条线（cubic spline line）连接[27]起来构造上包络线xmax(t)和下包络线xmin(t)。

（2）上包络线和下包络线的均值m(t)由式（2）得出：

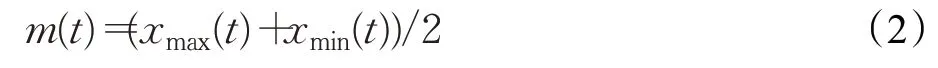
（3）从原始时间序列中减去m(t)以获得分量l(t)：

（4）检查l(t)序列是否满足上述中作为IMF分量的两个条件。如果满足这两个条件，则用l(t)替换x(t)；如果不满足，则重复步骤（1）～（3），直到l(t)满足作为IMF分量的两个判定条件。此时，l(t)为一个IMF分量，令l(t)等于Imf1(t)。通过式（4）从原始流量序列x(t)减去Imf1(t)以得到残差项r1(t)：

然后，将r1(t)作为更新后的新原始流量序列。重复步骤（1）～（3），获得Imf2(t),Imf3(t),…,Imfn(t)分量，最后得到残差项序列rn(t)。原始流量序列与各分量之间的关系见式（5）：

通过上述过程，原始的基站小区网络流量序列可以分解为若干个IMF分量和一个残差项分量。基站小区网络流量波动性较大，导致在使用EMD分解时容易发生“模式混合”现象，为了解决EMD存在的“模式混合”问题[28]，Wu和Huang[29]提出了集合经验模式分解方法。EEMD的思想是利用白噪声具有频率均匀分布的特性，把高斯白噪声添加到信号中，使信号在不同尺度上具有连续性，从而改变了信号极值点特性，促进抗混分解，有效避免模式混合现象。为此，本文采用EEMD取代EMD来分解流量信号。EEMD分解步骤如下[30]：

（1）初始化EEMD中的参数，如白噪声幅度。

（2）在初始基站小区网络流量x(t)中添加M次白噪声：

其中，wj(t)表示第j次添加白噪声序列，xj(t)表示第j次添加白噪声后网络流量。

（3）通过EMD将添加了白噪声的网络流量序列xj(t)分解为n个IMF分量Imfj i(i=1,2,…,n)和残差项分量之和。

（4）计算添加M次白噪声后得到流量的IMF平均值，作为最终IMF分量。

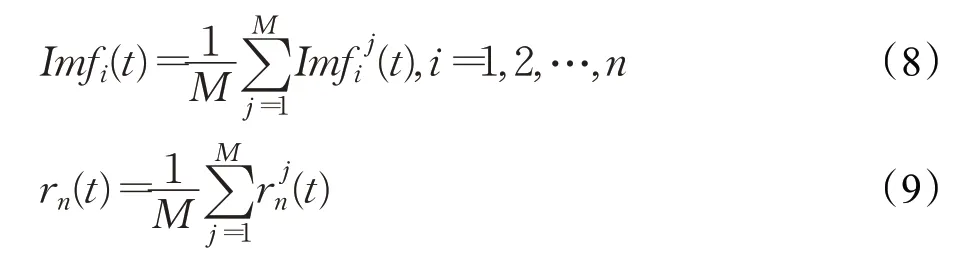
2.3 Prophet模型

Prophet使用pyStan开源工具中的L-BFGS（limited memory Broyden-Fletcher-Goldfarb-Shanno）方法[31]进行函数的拟合。L-BFGS是解无约束非线性规划问题最常用的方法。Prophet模型通过式（10）对时间序列进行拟合：

其中，y(t)∈{Imf1,Imf2,…,Imfn,rn(t)}；g(t)为趋势项函数，适合非周期性序列建模；s(t)为季节项（周、月、季度和年等）函数，用于对周期性变化明显的序列进行建模；h(t)为某固定时间段（例如节假日等）引起的变化函数；ϵt表示噪声项。

本文使用简单的分段常数函数对趋势项g(t)进行拟合：

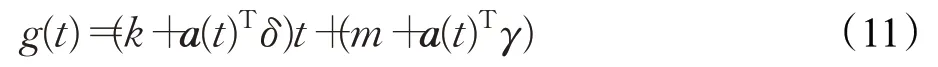
其中，k～Normal(0,5)为流量增长率参数δ(δ∈ℝS)为调整增长速率的增长率向量，m～Normal(0,5)为偏移量参数。

季节项s(t)通过式（12）来拟合，如果流量数据是以天为单位，那么数据可能存在年周期性和星期周期性。

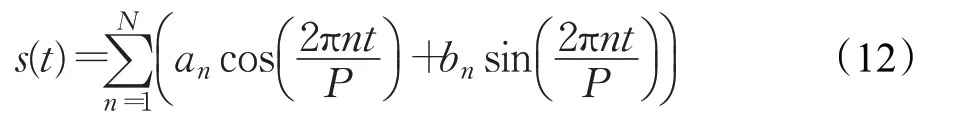
由于本文中基站小区网络流量数据的时间跨度小于一年，因此不具有年周期性而具有星期周期性。式（12）中P表示周期，当设定时间序列按照几天为周期，则设定P等于几，在此设定按星期为周期，所以将P设为7。N作为低通滤波器参数，对于具有星期周期性的序列，当N设置为3时拟合效果较好[19]。

关于节假日项h(t)的拟合，假如有L个节假日，对于第i个节假日，使用Di表示该节假日所在的一段时间区间，参数κi来表示节假日时间区间Di的影响程度，则h(t)可表示为：

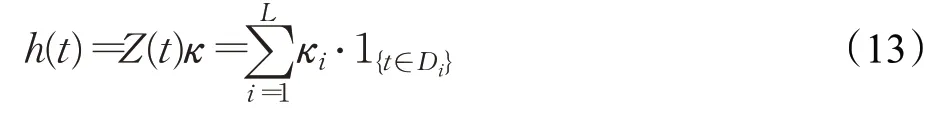
噪声项ϵt是一个服从正太分布的一个随机值。

3 实验过程

3.1 实验数据说明

实验中基站小区网络流量数据来源于某区域1 000个基站小区网络流量，单位为KB。流量数据按天统计，每天的流量数据为自忙时的流量。流量数据的时间范围为2017年9月1日到2018年3月31日，选取2017/9/1—2018/2/28共175天的有效流量数据作为模型的训练集，选取2018/3/1—2018/3/31共31天的流量数据作为模型的测试集。

3.2 预测性能评估指标

鉴于网络流量数据数量级较大，本文选择均方对数误差根（RMSLE）指标来评价模型预测性能，该指标越小表示预测越准确。

其中，N表示要预测流量的天数，表示网络流量预测值，yi表示网络流量真实值；当评价多个小区预测结果时，N为要预测流量的天数与基站小区数量的乘积。

3.3 实验设置

本文将E-Prophet模型与SARIMA、LSTM、Prophet以及EMD-Prophet四个模型进行对比。Prophet模型如前所述，其他三个模型说明如下：

SARIMA模型：季节性差分自回归滑动平均模型（SARIMA）通过对时间序列进行变换和拟合来建模。其中ARIMA模型在拟合平稳过程时表现出很强的适用性，同时对于数据的时间趋势可以进行差分变换，使其转化为平稳的时间序列数据，相应地得到预测结果后也要进行差分还原。

LSTM模型[32]：LSTM是循环神经网络的一种类型，它通过记忆长时间的信息来解决长期依赖性问题。LSTM网络由LSTM单元组成，每个LSTM单元由以下几个部分组成：（1）一个细胞，（2）一个输入门，（3）一个输出门，（4）一个遗忘门。通过对神经网络设定合理的输入输出步长来训练网络参数。

EMD-Prophet模型：与E-Prophet模型类似，差别在于利用EMD对基站小区网络流量进行分解。

以上模型的参数设置为：（1）对于SARIMA模型，通过网格搜索的方式[33]来确定其参数，预测步长设为31天。（2）对于LSTM模型，输入步长设为18，输出步长设为3。由于预测时长为31天，通过滑动窗口的方式把预测的3天的数据作为输入，以此类推，迭代11次预测未来33天数据，并取前31天数据值作为最终预测结果。（3）对于Prophet模型，使用星期周期和月周期参数，预测步长参数为31天。

通过设置以下实验场景对各种模型进行比较和验证：场景一，使用EMD和EEMD方法对基站流量进行分解，以此比较两种方法的流量分解效果；场景二，在单基站长期预测中对各个模型预测性能进行比较，以此观察不同预测模型的拟合效果；场景三，在多基站长期预测中对各个模型预测性能进行比较，以此来对比不同模型长期预性能；场景四，在缺失数据情况下对不同模型预测性能进行比较，以此分析模型的鲁棒性。

实验环境的硬件配置：Intel®CoreTMi7-6700 CPU@3.40 GHz，22核，64 GB内存。软件配置为：Python3.7.3，tensorflow1.15，fbprophet0.5，EMD-signal[34]0.2.10。

3.4 EMD/EEMD流量分解效果对比

为了比较EMD和EEMD对于流量分解的效果，随机从1 000个基站小区选取一个基站作为案例研究。原始基站小区网络流量数据如图2所示，图3和图4分别表示EMD和EEMD对原始数据流量进行分解的效果。

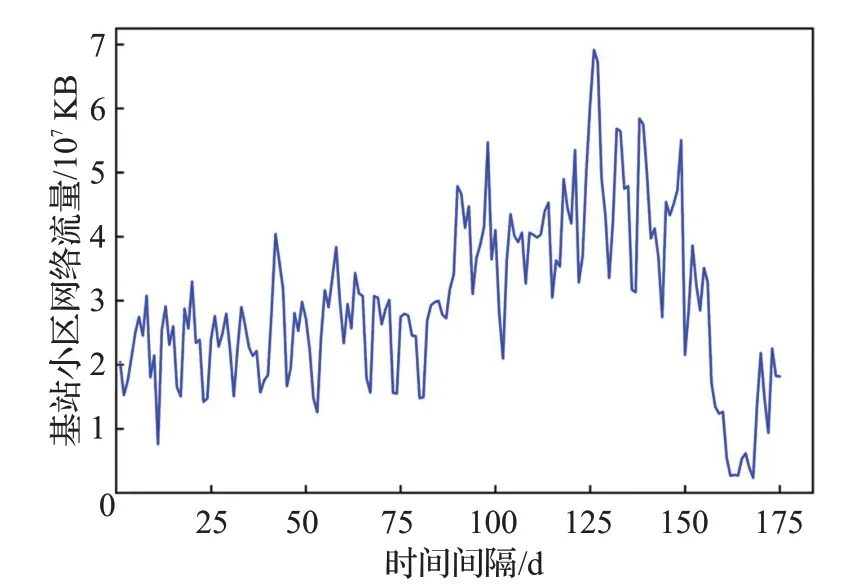
图2 某基站原始网络流量训练集Fig.2 Raw network traffic training set for base station

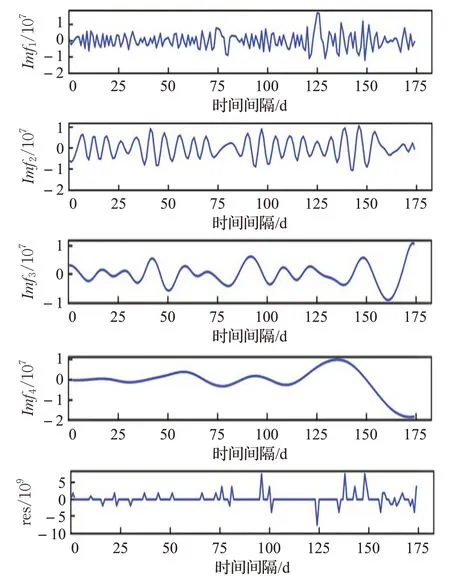
图3 某基站原始网络流量的EMD分解Fig.3 EMD decomposition of base station’s raw network traffic training set

通过图5可以看出，原始的网络流量按星期进行划分之后，周六、日的采集流量值普遍比其他星期采集的流量值小。通过图6可得，Imf1分量不同星期流量都比原始分量更加平稳。通过图7可得，Imf2分量不同星期流量值分布区间有显著区别。

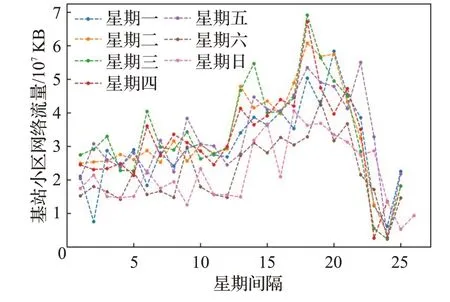
图5 某基站原始网络流量按星期划分Fig.5 Raw network traffic training set of base station divided by week

通过图8可得，Imf3分量不同星期对应的网络流量具有相似的周期性。通过图9～11可得，其他分量不同星期所对应的网络流量具有相似的趋势性，而且不同星期取值呈现一定的按星期周期交换的规律，即不同星期对应的流量大小顺序，会随着星期间隔变化而呈现出一定的周期性。这是因为原始数据流量经过EEMD分解后的各个分量具有一定的平稳性、趋势性以及按星期周期变化的规律。

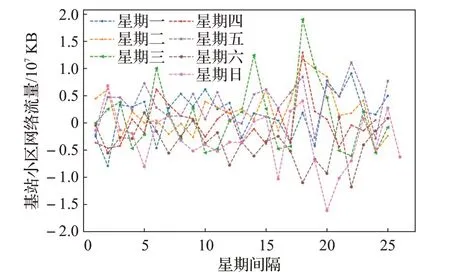
图6 Imf1分量按星期划分Fig.6 Imf1 components by day of week

图7 Imf2分量按星期划分Fig.7 Imf2 components by day of week

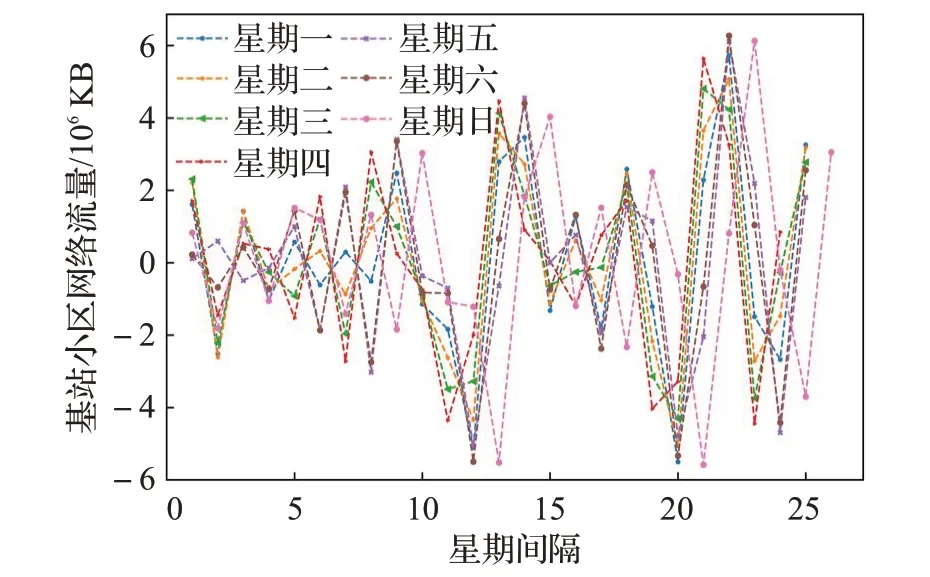
图8 Imf3分量按星期划分Fig.8 Imf3 components by day of week

综上可看出，相对于EMD，EEMD能使分解的序列表现出更好的平滑性、平稳性以及趋势性和周期性，更加适合Prophet模型的拟合。

3.5 单基站不同模型预测结果对比分析

本节对3.4节案例研究中的基站小区使用不同模型进行预测，预测步长为31天，结果对比如图12所示。

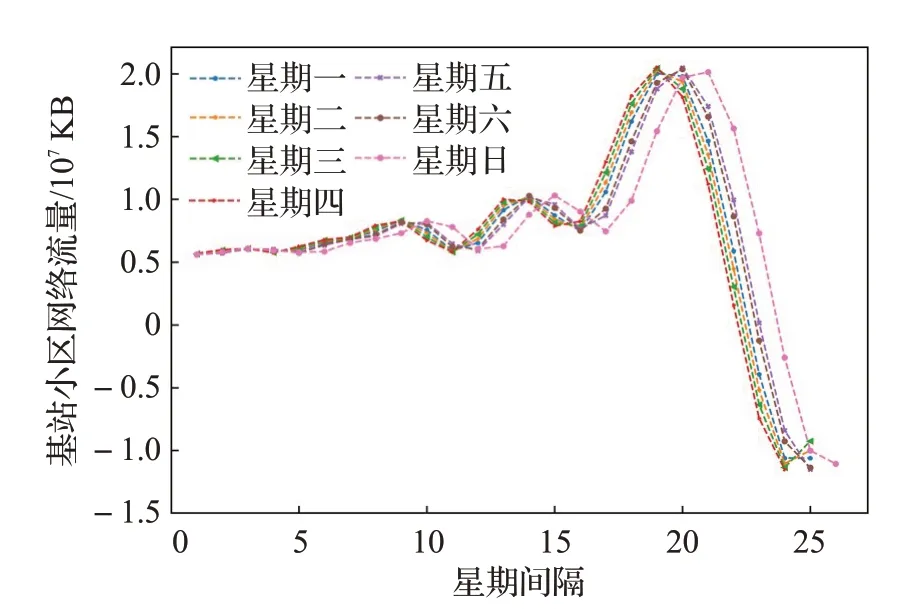
图9 Imf4分量按星期划分Fig.9 Imf4 components by day of week

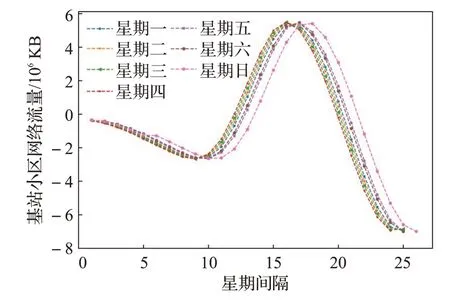
图10 Imf5分量按星期划分Fig.10 Imf5 components by day of week

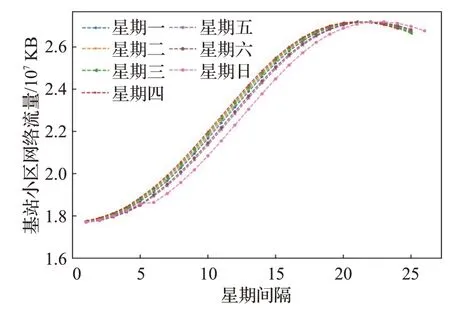
图11 残差项分量按星期划分Fig.11 Residual components by week

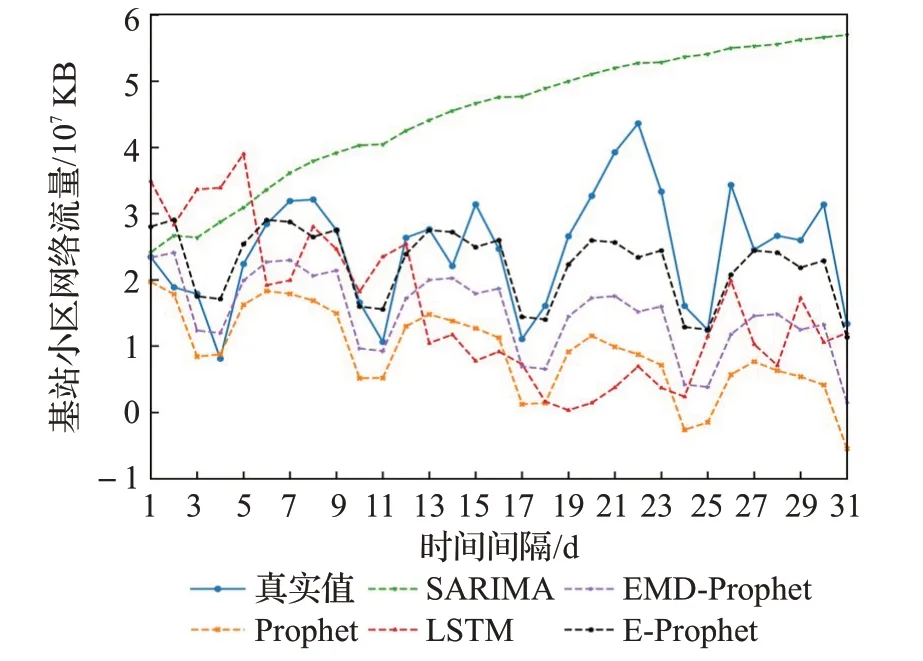
图12 某基站不同模型预测结果对比Fig.12 Comparison of prediction results of different models of base station

由图12可看出，真实流量值有一定的周期性，而Prophet、EMD-Prophet和E-Prophet能识别这种周期变化的特性和趋势。SARIMA长期预测结果优于Prophet，但从图中预测结果看，在长期预测中SARIMA拟合趋于一条直线。由于使用EMD/EEMD分解后的数据平稳性更好，因此结合EMD/EEMD和Prophet模型的预测结果优于Prophet模型。此外，与EMD相比，EEMD避免了因极值点分布不均匀导致的“模式混合”现象，而且分解后的残差项趋势性更显著。因此使用E-Prophet（EEMD+Prophet）预测效果优于EMD-Prophet模型。分别计算上述不同模型预测结果的RMSLE值，如表1所示。由表1可看出E-Prophet模型的预测性能最好。

表1 不同模型预测某基站小区流量的RMSLE值Table 1 RMSLE value of base station cell traffic predicted by different models

3.6 多基站不同模型长期预测结果分析

上节对单基站的预测性能并不能代表模型的整体预测性能，本节对多基站网络流量进行预测。为此，对875个基站小区流量进行了长期预测。需要说明的是，在1 000个小区中，有些小区具有较多的零值网络流量，SARIMA无法利用网格搜索找到最佳参数导致无法预测。为方便对比，选取SARIMA能够预测的所有875个基站小区流量。预测步长范围为16～31 d。预测结果对比和统计分别如图13和表2所示。

图13 多基站不同模型长期预测结果对比Fig.13 Comparison of long-term prediction results of different models for multiple base stations

综合图13和表2可以看出，EMD/EEMD结合Prophet的模型在长期预测中优于Prophet、SARIMA和LSTM模型。这是因为EMD和EEMD方法可以把时间序列分解成平稳性和趋势性更显著的分量，同时保持原有时间序列的周期特征，最后通过Prophet模型对这些分量进行更准确的预测。

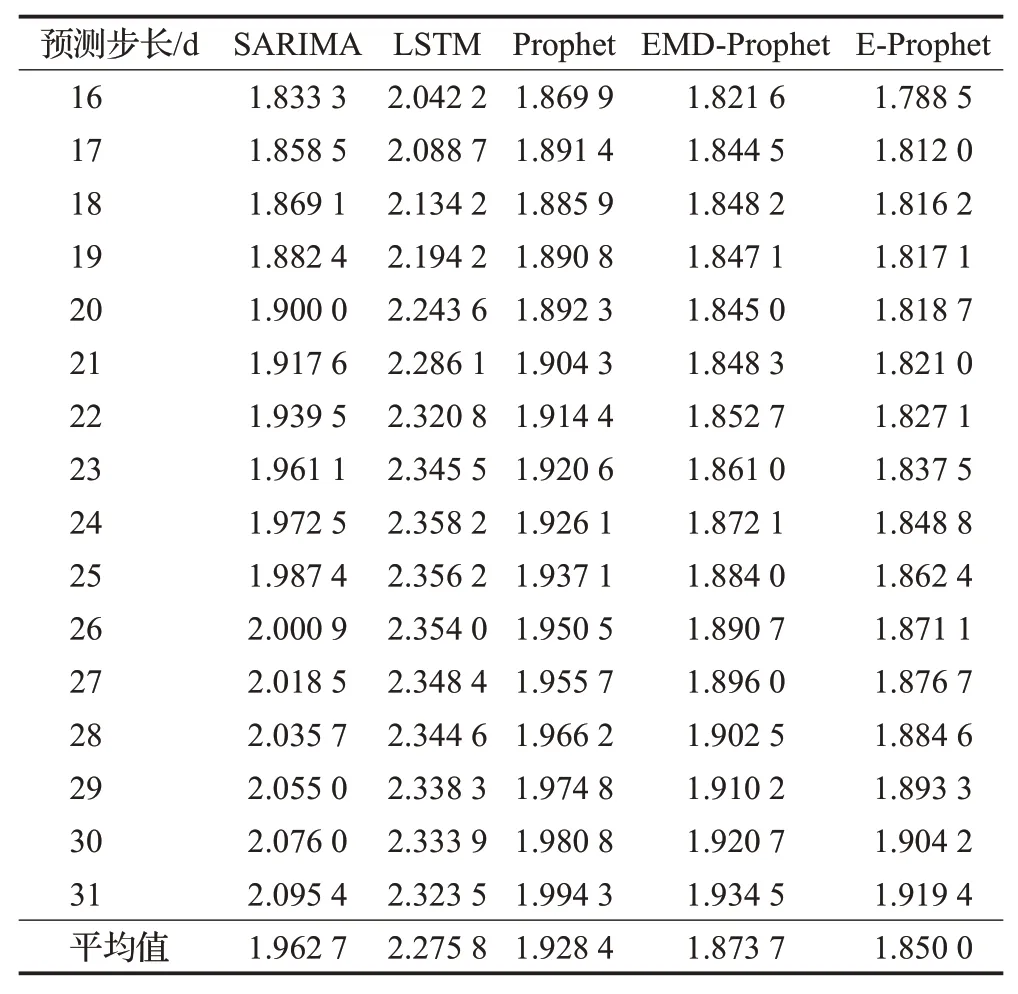
表2 多基站长期预测的RMSLE值对比Table 2 Statistical comparison of long-term forecast RMSLE data for multiple base stations

3.7 鲁棒性实验结果分析

为了验证E-Prophet模型的鲁棒性，对不同模型在缺失数据环境下的预测性能进行对比。选取125个零值数据较多的基站进行实验，结果见图14和表3。

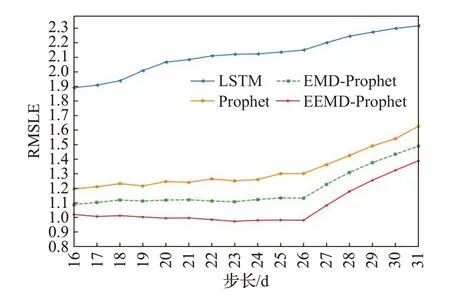
图14 多基站不同模型鲁棒性结果对比Fig.14 Comparison of robustness results of different models of multiple base stations

从中可看出，结合EMD/EEMD和Prophet的模型在长期预测中优于Prophet模型、LSTM模型、EMD-Prophet模型。这是因为Prophet模型能通过计算训练集数据概率分布和周期性来确定相应参数，从而在缺失值较多的小区依然能较好预测。SARIMA对于以上零值较多的基站小区，无法得出预测结果。

4 结语

由于网络流量具有非线性、非平稳的特点，因此难以准确地进行长期预测。本文提出基于Prophet混合模型的基站网络流量长期预测方法，通过实验得出以下结论：（1）EEMD可将流量序列分解为一组平稳或较平滑的分量，适合处理基站小区网络流量序列；（2）EEMD使得每个IMF分量和残差项具有清晰的物理含义、IMF分量更平稳，从而使得Prophet模型对每个IMF分量和残差项有更好的预测效果，并且采用EEMD比采用EMD的预测准确性更高；（3）EMD/EEMD结合Prophet的组合模型在长期预测中比Prophet、LSTM、SARIMA模型的准确性、鲁棒性更好，并且E-Prophet优于EMD-Prophet模型。下一步研究工作将探索将概率模型算法和深度学习模型相结合的方法来解决多区域多基站联合预测的问题。

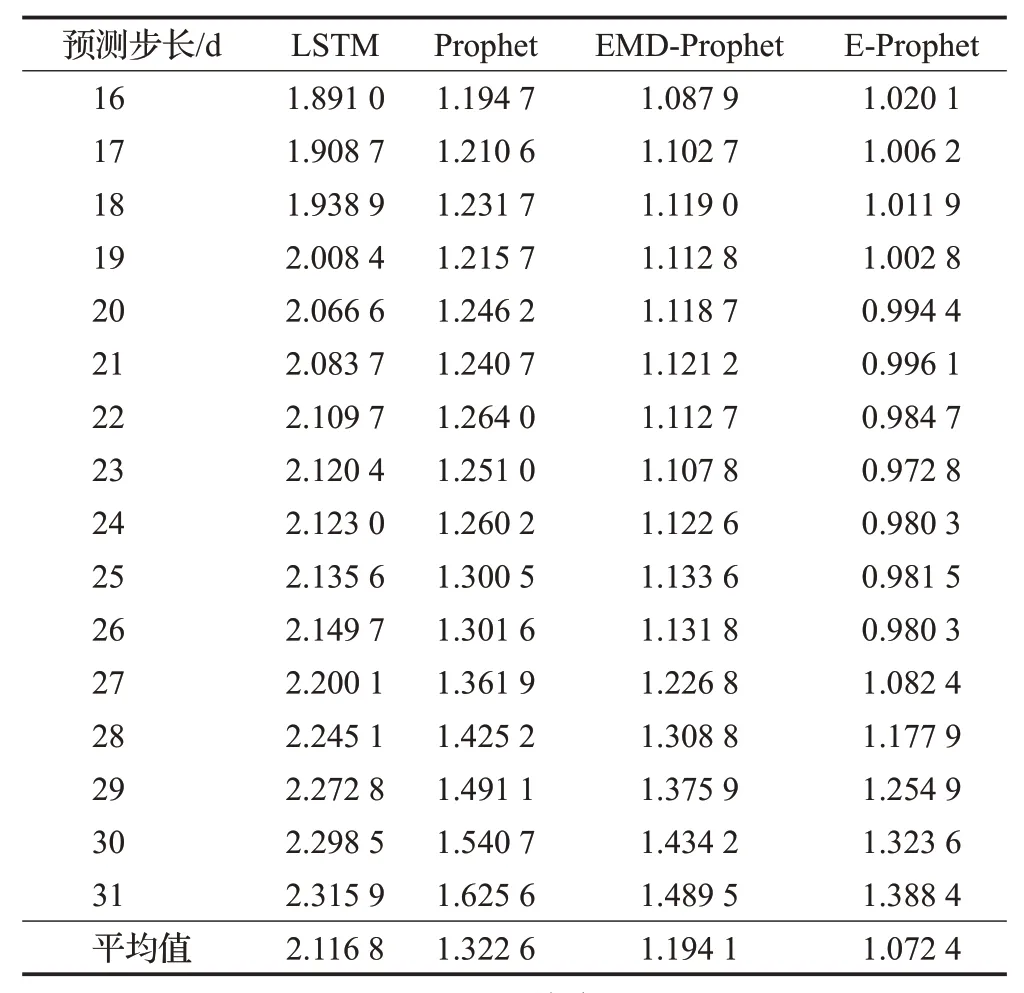
表3 多基站鲁棒性实验的RMSLE值对比Table 3 Statistical comparison of RMSLE data for multisite robustness experiments