段塞流输流管道的稳定性分析
2022-07-20吴明明杨翊仁
吴明明,杨翊仁,李 鹏
(西南交通大学力学与航空航天学院,成都 611756)
引 言
输流管道的动力学行为是一个典型的流固耦合现象,Paidoussis 等[1]认为输流管道已经成为结构动力学和稳定性研究的新模型,并归纳总结了输流直管、曲管的线性及非线性动力学问题,进一步对管道稳定性的研究做了系统化、理论化的阐述。
单相流输流管道是早期学者们的主要研究对象。Chang 等[2]研究了两端固支的输流层合圆柱壳的固有频率,发现其随流速的增大而降低。张瑞平等[3]通过有限差分法,分析了轴向力对两端支撑管道稳定性的影响,认为轴向力的增大会导致失稳临界流速的增大。初飞雪[4]进一步发现,两端支撑管道的固有频率会随着管内压力增大而减小,并且会随管长的增大而明显减小。张挺等[5]采用有限差分法对管道振动微分方程进行离散,研究了输流直管在不同边界条件下的振动及响应特性。Huang 等[6]使用伽辽金消元法得到了不同边界条件下管道固有频率的计算公式。易浩然等[7]基于哈密顿原理建立了含有集中质量的悬臂输流管道的动力学模型,研究了集中质量对管道振动特性以及稳定性的影响。周坤等[8]和Yu 等[9]研究了由不同材料组成的周期性管道的稳定性和非线性动力学行为,认为当周期数达到某一临界值时,管道的失稳临界流速将趋于定值。刘颖等[10]对粘弹性输流管道的动力学微分方程进行了Laplace变换,研究了系统参数变化对管道自由端稳态响应的影响。王忠民等[11-12]采用有限差分法研究了弹性地基上输流管道的流速、地基密度等参数对管道固有频率的影响。马涛等[13]通过数值方法求解了功能梯度悬臂管道的振动方程,研究了材料的幂律指数、无量纲尺度参数及质量比对管道稳定性的影响。
与单相流近似稳态的流动不同,段塞流管道中气相、液相交替流动,成为了研究的难点。Wang等[14]研究了左端固支、右端简支的段塞流管道的响应特性,认为流体速度影响着离心力和科氏力,液塞段出管时对管道的响应有很大影响。Liu 等[15-16]分别用伽辽金方法和有限单元法对悬臂和左端固支、右端简支边界下段塞流管道的固有频率进行了研究,认为固有频率既受液体表观速度的影响,又受气体表观速度的影响。Khudayarov 等[17]建立了两相段塞流的粘弹性输流直管的动力学模型,发现增大气塞长度会降低振动响应的幅值和管道的固有频率,弹性地基密度会影响管道的失稳临界流速。Meng 等[18]研究了在外流作用下的两相段塞流柔性立管的涡激振动问题,计算了立管的响应,并通过实验验证了理论模型的正确性。此外,孔令钱等[19]使用ANSYS Workbench 仿真软件对流固耦合作用下的输流管道进行了仿真,计算了管道的频率及振型。
上述学者相继研究了段塞流管道的频率和响应,在稳定性方面却鲜有研究。因此,本文在段塞流管道固有频率的研究基础上,进一步对管道稳定性的内容进行补充。基于气、液两相段塞流管道的理论模型,采用伽辽金方法对系统振动方程离散,并进行数值求解,依据弗洛凯理论对系统稳定性进行判定,讨论各参数变化对管道固有频率均方根及失稳临界流速的影响,通过理论分析对段塞流管道的稳定性、可靠性进行评估,预防事故的发生。
1 气液两相段塞流管道理论模型
气液两相段塞流管道和段塞单元的模型如图1所示,图中蓝色区域表示液体,白色区域表示气体,L为管道长度,x方向为管内两相流体的运动方向,y方向为管道的横向运动方向,V为两相流流速,lu为段塞单元长度,lf、lg分别为段塞单元内液塞段和气塞段的长度。
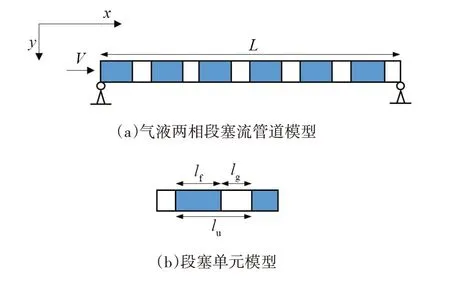
图1 气液两相段塞流管道及段塞单元模型
对管道结构和管内流体作如下假设:(1)管道具有较大的长细比,可用欧拉-伯努利梁模型来描述;(2)管道轴线不可伸长;(3)忽略管材及流体的阻尼;(4)管内气体、液体定常不可压缩,且保持相同的运动速度;(5)忽略重力、轴向压力的影响。
基于上述假设及文献[14],可以得到两相流管道的振动方程如下:
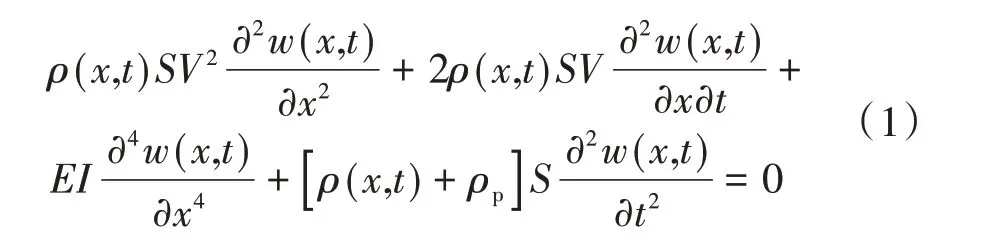
式中:E为管道弹性模量;I为管道的截面二次矩;S为管道横截面面积;w(x,t)为管道横向振动位移;x为管道沿轴向到入口处的距离;t为时间;ρp为管道密度;ρ(x,t)为管道内单位长度上两相流体的密度,其值根据时间t和空间x的不同,要么等于液体密度ρf,要么等于气体密度ρg。
假设管内存在n个完整的段塞单元,以管道右端出口处的段塞单元为研究对象,考虑该单元从管道内完全流出的过程,依次取图2 所示t1~t5的5 个不同时刻。t1时刻,该段塞单元中的气塞段准备出管;t3时刻,段塞单元中的气塞段完全出管,液塞段准备出管;t5时刻,整个段塞单元完全出管。t2是介于t1和t3的任意时刻,此时段塞单元中的气塞段部分出管;t4是介于t3和t5的任意时刻,此时段塞单元中的液塞段部分出管。t5时刻后管道中两相段塞流的运动状态又将回到t1时刻,即上述过程构成段塞流系统的一个运动周期,换言之,该系统是一个周期时变的线性系统。
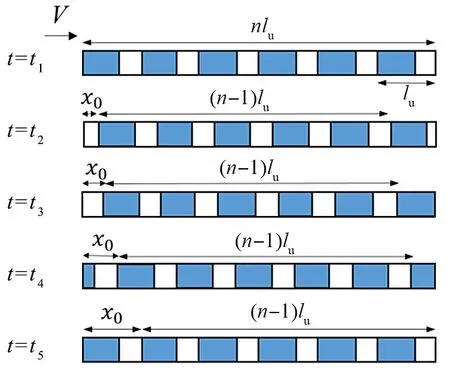
图2 不同时刻的管内流动状态
图2 中,x0表示在一个运动周期内管道入口与第一个完整段塞单元之间的距离,其表达式为:

假设t1为初始时刻,即要求t1= 0,根据已知的两相流流速V、段塞单元长度lu和气塞长度lg,可以得到t3、t5的表达式分别为:

选择简支梁的振型函数φ为基函数,并采用伽辽金方法对式(1)进行离散,通过对振动方程在管道长度L上进行积分,便可得到积分形式的气液两相段塞流管道的横向振动方程。
在一个运动周期内,当t1≤t
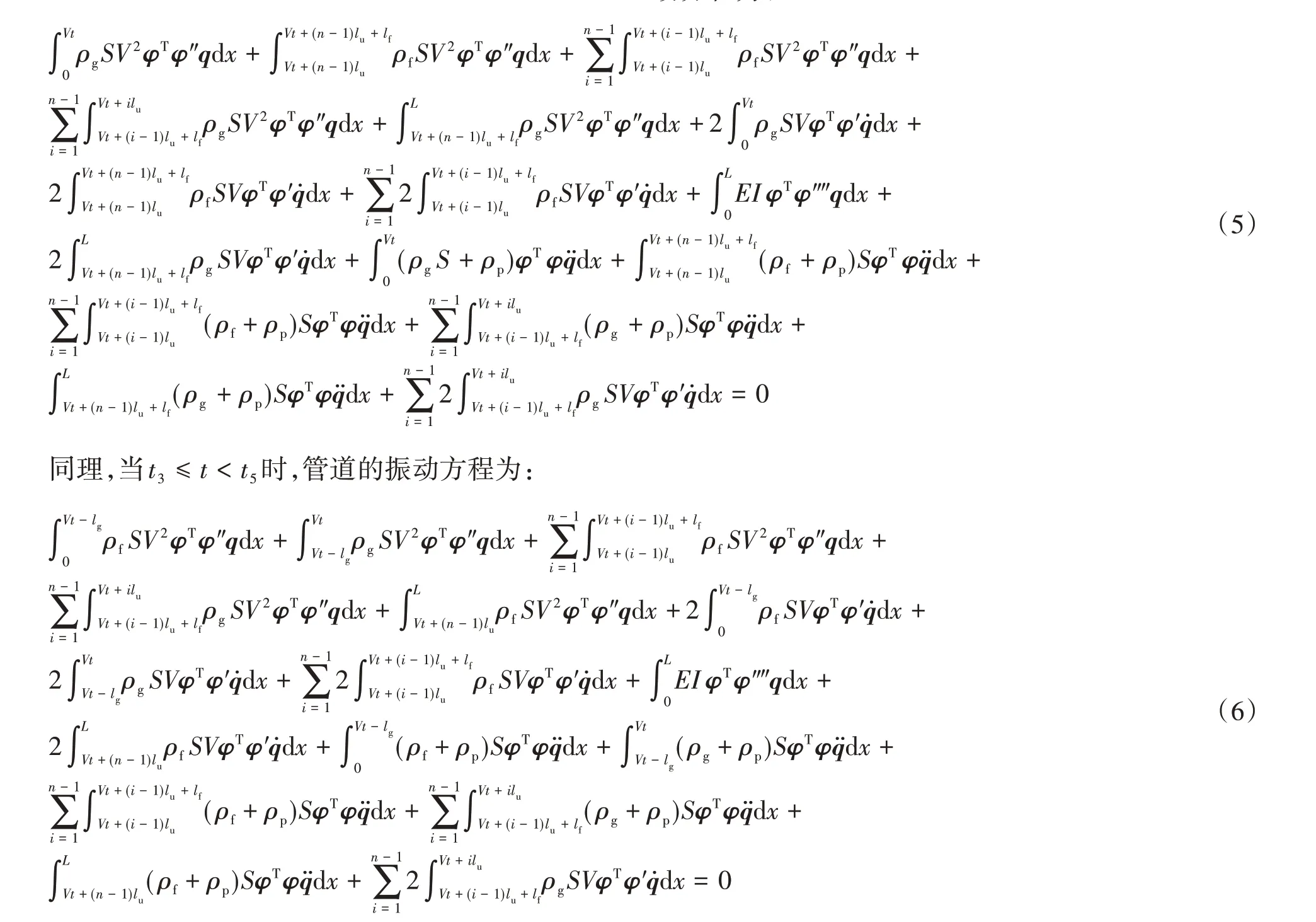
将上述方程改写成矩阵形式的表达式为:
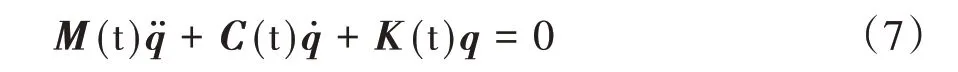
其中:M(t)、C(t)、K(t)分别为系统中与时间相关的质量矩阵、阻尼矩阵和刚度矩阵,q、q̇、q̈分别为系统的广义位移、广义速度和广义加速度。
定义如下矩阵和向量:
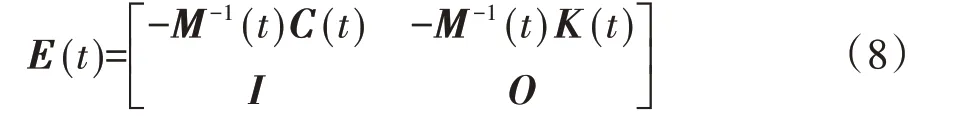

将其代入式(7)中,即可得到状态方程的标准形式:

令式(10)的解为:

其中:ω=ωr+iωi,ωi表示管道的固有频率,ωr表示与阻尼相关的衰减项。将解代入式(10)后,得到系统的特征方程为:

通过上述分析,便可将动力学方程转化为广义复特征值的问题进行求解。
2 理论模型的验证
在管道内径ri=5 cm,外径ro=6 cm,L=15 m,E=210 GPa,ρp=7850 kg/m3,ρf=1000 kg/m3,ρg=1.293 kg/m3,lu=5 m,lf=3 m,V=10 m/s 的条件下,通过对管道振动方程的求解,可以得到管道的一阶固有频率f1和二阶固有频率f2随时间的变化曲线如图3 所示,图中可见,管道固有频率是随时间周期变化的。
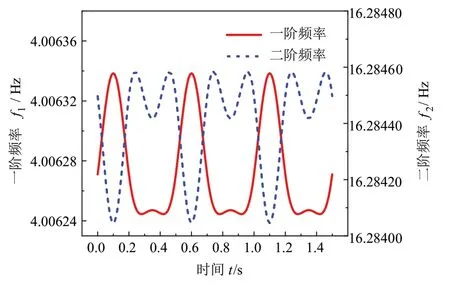
图3 管道前两阶固有频率随时间的变化曲线
当段塞单元中的气塞长度为零时,即段塞单元长度等于液塞长度,这表示气液两相段塞流模型完全退化为单相流管道模型,周期时变系统也变为定常系统,此时管道的固有频率为恒定的常数。计算本模型在该条件下的固有频率,并通过与Huang等[6]关于单相流管道系统固有频率的计算结果进行对比,即可完成本文中气液两相段塞流理论模型的验证。
在系统参数保持不变的条件下,控制两相流流速V从2 m/s 增加至34 m/s,计算得到本文模型与Huang模型[6]的一阶固有频率f1随流速V的变化曲线如图4 所示,图中可见,二者的计算结果高度吻合,验证了本文理论模型的正确性。
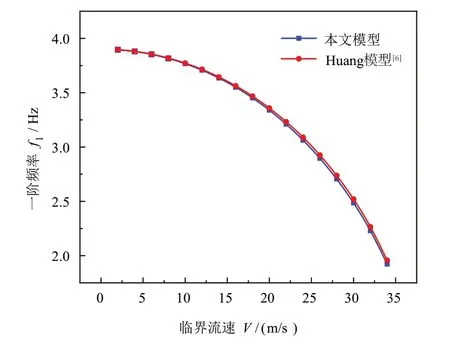
图4 两种模型的一阶频率随流速的变化曲线对比
3 临界流速预测与频率参数研究
对于两端简支的单相流输流管道,通常会基于线性定常系统的稳定性准则对管道进行稳定性分析。考虑到图3 中的一阶频率的周期波动幅值在0.0001以下,因此在对频率的精度要求不高时,完全可以将一阶频率视为常数,故可以对本文的周期时变系统进行拟定常化的分析,缺点在于会产生微小的误差。为了便于分析,考虑用单周期内的频率均方根值来表征系统的固有频率。
假设系统参数lu、lf、L、ρg、ρf、ρp的参考值分别取1 m、0.5 m、10 m、1.293 kg/m3、1000 kg/m3、7850 kg/m3,式(12)的特征值实、虚部的均方根随两相流流速的变化曲线如图5 所示,图中可见,系统的一、二阶频率均随流速的增大而降低,而且一阶频率会率先降低至零。依据线性定常系统的稳定性准则,可以推断当流速约为83.3 m/s 时,特征值的一阶虚部均方根等于零、一阶实部均方根大于零,表明管道系统发生失稳。
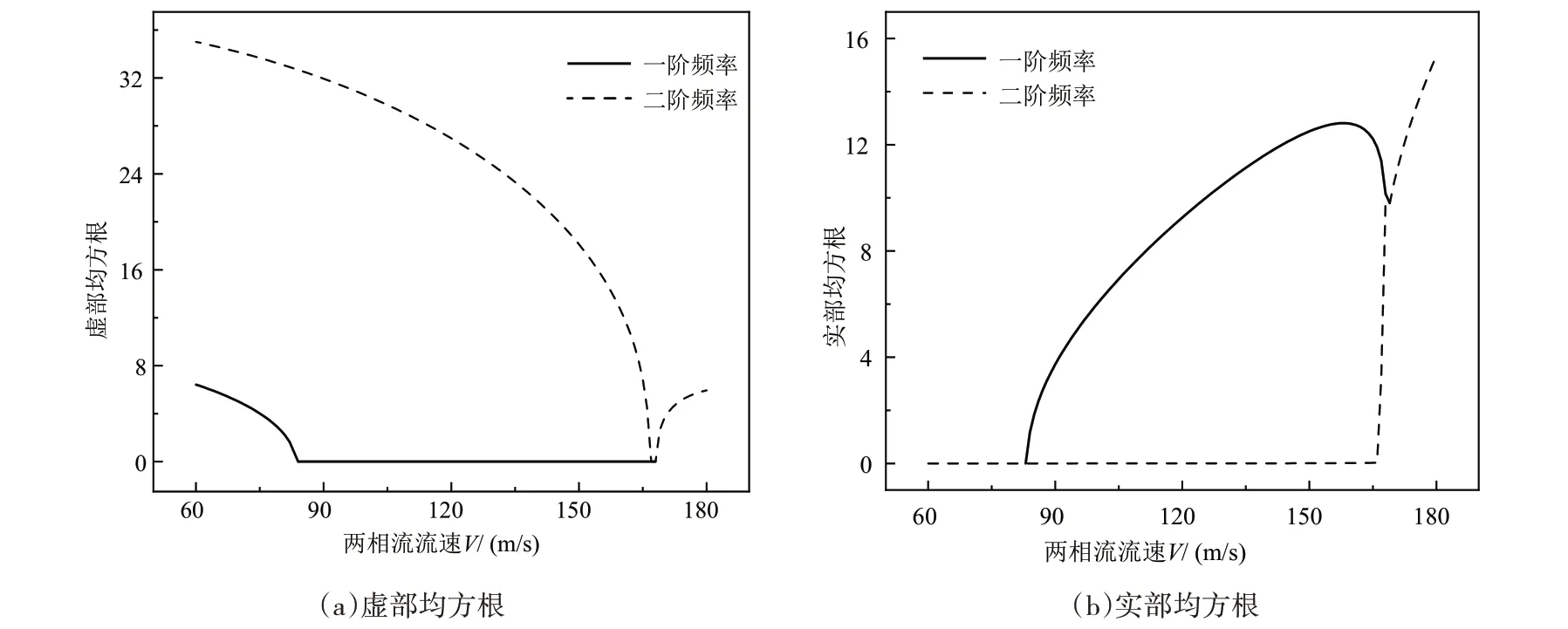
图5 系统特征值虚、实部均方根随两相流流速的变化曲线
通过改变某一参数,其他参数分别取对应的参考值时,得到管道的一、二阶频率f1和f2随参数的变化曲线如图6所示。由图6(a)、图6(d)可以看出,段塞单元长度和气体密度的变化对管道一、二阶固有频率的影响较小;从图6(b)~6(f)中可以发现,管道的一、二阶固有频率均随液塞及管道长度、液体及管道密度的增大而明显降低,且当管道长度增大到某一临界值时,频率均方根会逐渐降低至零。
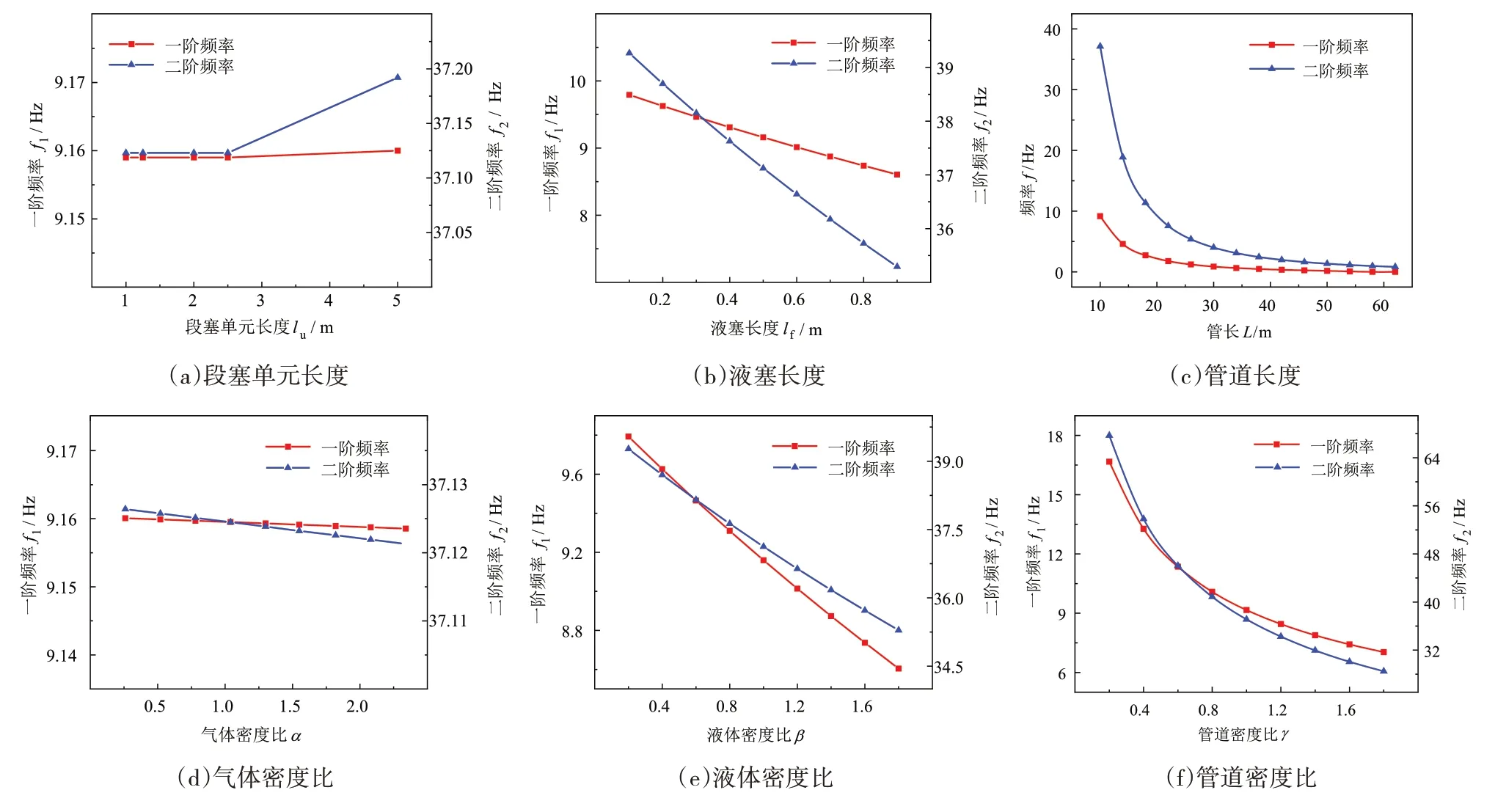
图6 管道固有频率随系统参数的变化曲线
4 稳定性及其参数研究
4.1 稳定性判定
周期性时变系统[20]的特征值是随时间周期变化的,分析时需要将其转化为定常系统,再根据定常系统的系数矩阵特征值模的大小来判断原系统的稳定性。
式(10)中系数矩阵E(t)的周期为T,且满足E(t) =E(t+T),假设该系统的标准基解矩阵为Z(T),即要求Z(T)是如下微分方程组的解:其中I为单位矩阵。

引入李雅普诺夫变换:

其中L(t)为李雅普诺夫变换矩阵。将式(14)代入式(10),即可将周期时变系统转化为定常系统:

式中H为该定常系统的系数矩阵。通过计算系数矩阵特征值的模,并将计算结果与数值1进行比较,即可完成原系统稳定性的判断。
当系统参数取参考值时,分别计算流速为83.2 m/s、83.3 m/s 和83.4 m/s 时矩阵H的特征值γ1和γ2的模,计算结果见表1。
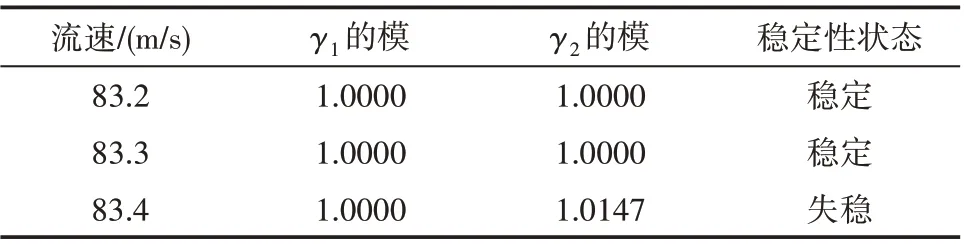
表1 不同流速下矩阵H特征值的模对应的系统状态
由表1 可见,当流速大于83.3 m/s 时,系统特征值的模有一个大于1,表明管道已经发生了失稳,这与第3 节中管道失稳临界流速的预测结果一致,验证了通过固有频率均方根来预测失稳临界流速的可行性。
4.2 稳定性的参数研究
为了研究参数lu、lf、L、α、β、γ变化对管道稳定性的影响,通过改变其中某一参数,其他参数分别取对应的参考值,得到管道失稳临界流速随参数的变化曲线如图7 所示。从图7(a)与图7(d)中可以发现,段塞单元长度和气体密度变化对管道临界流速的影响较小;从图7(b)~7(e)中可以发现,临界流速会随着液塞及管道长度、液体密度的增大而呈现显著下降的趋势。从图7(f)中可以看出,临界流速不随管道密度的改变而发生变化。
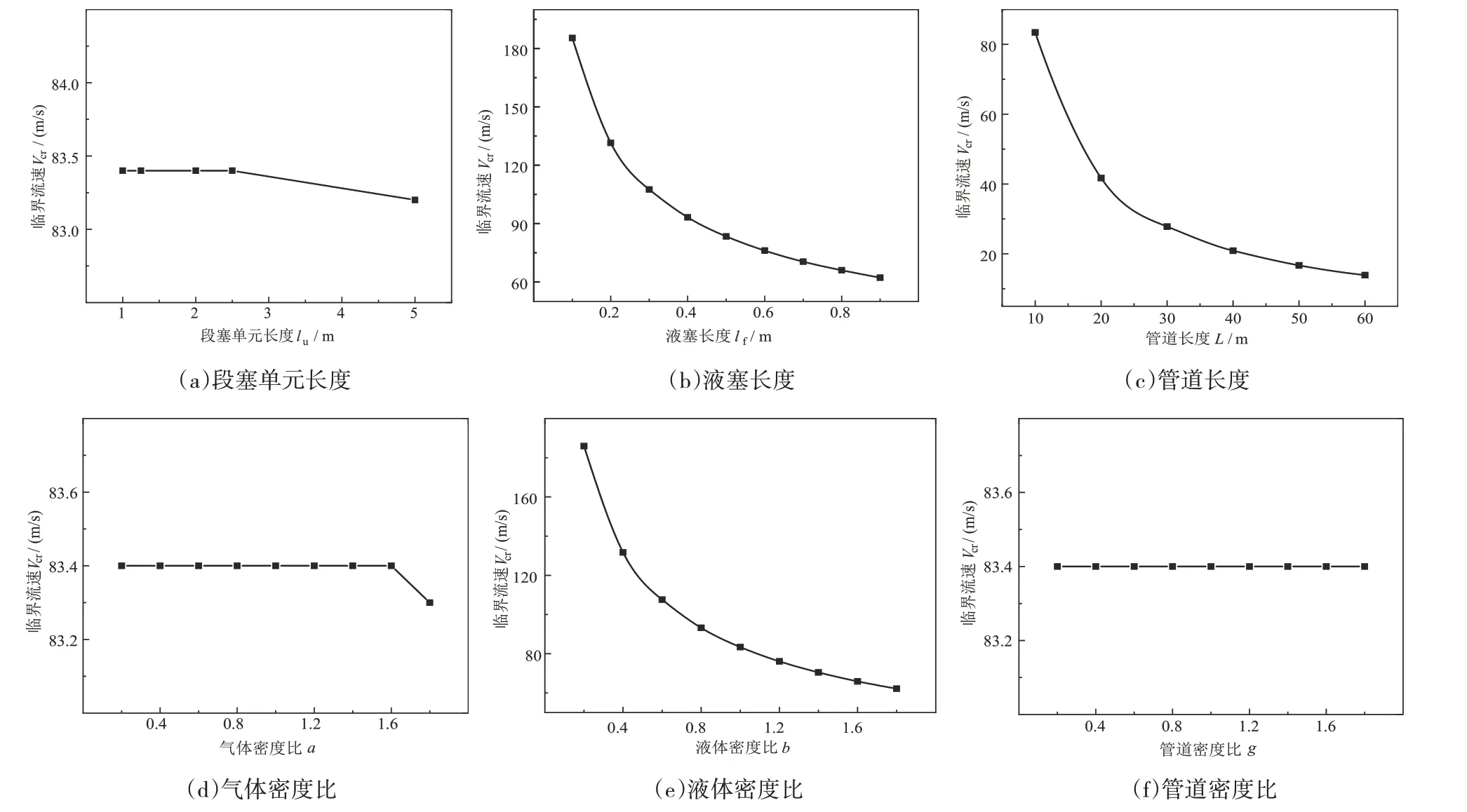
图7 失稳临界流速随系统参数的变化曲线
5 结论
基于气、液两相段塞流管道的理论模型,采用伽辽金方法对系统振动方程离散并进行数值求解,讨论了参数变化对管道振动特性的影响,并运用弗洛凯理论确定了管道的失稳临界流速,分析了参数变化对段塞流输流管道稳定性的影响。主要结论如下:
(1)气液两相段塞流管道的固有频率是随时间周期性变化的,且波动周期与管内流速和段塞单元长度有关。
(2)管道固有频率的均方根随流速、液塞及管道长度、液体及管道密度增大而减小,受段塞单元长度和气体密度的影响较小。
(3)管道的失稳临界流速随液体密度、液塞及管道长度的增大而减小,受段塞单元长度和气体密度的影响较小,且不随管道密度的变化而发生改变。
