洞门斜切斜率和车速对隧道气动性能的影响

张宗发，张明禄

（西南交通大学力学与航空航天学院，成都 611756）

引 言

我国幅员辽阔且多山多河流，致使高铁隧道数量多、路线长和运营车速快[1]。高速列车在通过隧道过程中会对隧道壁面和车体表面起瞬态冲击作用[2]，对列车运行的安全性、平稳性及隧道结构使用寿命等造成严重影响。

与明线上的桥梁等其他结构相比，隧道是封闭空间，当高速列车由平坦地面通过隧道过程中，列车表面受到的瞬变压力剧烈程度显著增加[3]。当列车以较高车速进入隧道时，在隧道内形成的压缩波向隧道口外传播时，导致在洞口外形成的微压波会对周围环境造成不良影响[4-5]。基于以上原因，减小隧道气动性能的不良影响是铁路隧道设计中必须解决的关键问题。因而优化列车外形或减速进入隧道可有效改善隧道气动性能而成为各个国家优先采取的措施[6]。为此，研究人员也通过大量的数值模拟研究[7-8]和现场实测[9-10]等手段探索高速列车通过隧道时的气动性能。

近年来国内外诸多学者以隧道空气动力效应的影响为指标，分别研究了高速列车通过带有不开口型缓冲结构[11]、开口型缓冲结构[12]、减压通道[13]以及等环斜切式洞门[14]等缓冲结构隧道时的气动特性，并应用于实际施工中。新型隧道洞门形式必然会对隧道空气动力学效应产生影响[15-16]。因帽檐斜切式隧道洞门相比于其他洞门形式能更大程度上减小微压波对附近环境的危害，从而被广泛应用于国内，如京沪和武广等多条新建铁路[17]，因此有必要继续深入分析其对隧道气动性能的作用。

为此，通过建立隧道-列车-空气三维计算流体动力学（CFD）数值仿真模型进一步研究帽檐斜切式隧道洞门对列车通过隧道时的流场特性影响，分析高速列车在不同车速和洞门斜切斜率的情况下驶过隧道过程中隧道中部监测点初始压缩波和车体表面压力及隧道口外微压波的变化，并研究车头鼻尖处压力幅值、压力波幅值、微压波幅值和初始压缩波最大压力梯度幅值与车速之间的关系，为后续列车隧道内运行的安全性评估提供参考。

1 数值模型

1.1 控制方程

高速列车在通过隧道的过程中，列车处于移动状态，因此该过程属于瞬态问题；隧道内的空气受到列车表面和隧道壁面的挤压，所以须采用可压缩的理想气体处理；而在列车周围的气流因受到强干扰，雷诺数一般大于106，流场处于湍流状态[18]。基于以上原因，采取常用的RNGk-ε双方程湍流模型来模拟列车通过隧道时的流场变化过程，控制方程表示如下：

连续性方程：

能量守恒方程：

湍流动能方程：

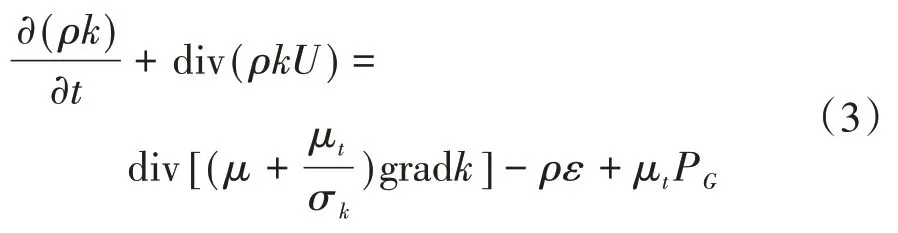
湍流动能耗散方程：

1.2 几何模型及边界条件

图1（a）所示为基于我国常用的CRH 系列列车，忽略受电弓、挡风板等结构，建立的简化3 编组模型，长约76 m。计算中，将车体表面的边界条件设为无滑移壁面。图1（b）所示为初始时刻列车-隧道-空气三维模型布置图。当列车开始运行时，列车头部距隧道洞口缓冲结构约90 m；在隧道两端外部大气场采用半径为190 m，长250 m 的半柱体模拟。半柱体的外边界条件设为压力出口边界。中间为隧道段，隧道长为400 m，并根据我国高速铁路的单洞单线标准断面设置适用于最高时速达350 km/h 的隧道横截面积，净空面积为100 m2。隧道入口分别采用3 种不同的隧道洞门斜切率（斜切段高度H与斜切段长度L的比值），即斜切率分别为1∶1.00、1∶1.75 和1∶2.00，如图1（c）所示。隧道壁面和帽檐斜切式结构壁面的边界条件均设置成粗糙度为0.5的无滑移壁面。

图1 几何模型及边界条件示意图

1.3 网格模型

建模过程中对列车及隧道模型均采用结构化六面体网格进行划分，如图2 所示。其中对列车及附近的空气运用滑移网格实现列车与地面的相对运动[19]。静止区域和移动区域通过交界面进行流场信息交换。为准确模拟列车在通过隧道过程中的车身周围流场演化，将列车表面的第1 层网格厚度设为0.001m，并按1.15 的比率扩展30 层，之后再以较大比率增长，高速列车及隧道模型整体网格数为880多万。

图2 列车表面网格图

2 结果分析

2.1 隧道内静压随时间的变化

列车在隧道环境运行时与在明线平坦地面相比存在明显差异。列车驶入隧道时，列车车头前方的空气随列车一起向前流动，并受到挤压，导致该处的空气压力上升。该处压力上升的空气又推动相邻的静止空气向前流动，这样循环往复的推动便造成隧道内压缩波的产生，该压缩波传到隧道内中部监测点时，瞬变压力迅速上升，直至达到最大峰值便形成初始压缩波；压缩波以近似声速的速度沿隧道长度向出口端传播，达到出口端时，大部分向隧道内反射，形成膨胀波，另一小部分向隧道外辐射，形成微压波。在列车车尾进入隧道瞬间，隧道内流入到列车后方的空气量小于列车所排挤开的空气量，且隧道外的空气在该时刻流入到列车车尾处。该瞬间列车尾部的压力低于隧道外大气压，形成负压，便产生膨胀波[20]。为了解隧道内压力波的变化规律，本节取隧道中部监测点为研究对象。

2.1.1 洞门斜切斜率对隧道内压力波的影响

高速列车在3 种不同斜切斜率条件下，以300 km/h的车速驶过隧道过程中隧道中部监测点的压力波变化曲线对比如图3 所示。由图3 可以看出，改变隧道洞门斜切斜率对隧道中部监测点的压力波变化趋势几乎无影响。即在t= 1.08 s 左右，列车车头开始驶入隧道缓冲结构时，该监测点压力开始波动；在t= 1.64 s 压缩波传到该点时，压力开始迅速上升。在驶入过程中由于列车表面和隧道壁面作用于空气的摩擦力效应和车身长度均在逐渐增加，导致压缩波突增一段时间，至t= 1.99 s 列车完全驶入隧道缓冲结构后压缩波变为缓慢升高，在t= 2.55 s 时，该监测点压力达到峰值。之后因为在车尾处产生的膨胀波传播至该监测点，导致该处压力急剧下降，直到t= 3.50 s 左右，列车车头鼻尖到达该监测点时，压力波达到最大负压值。

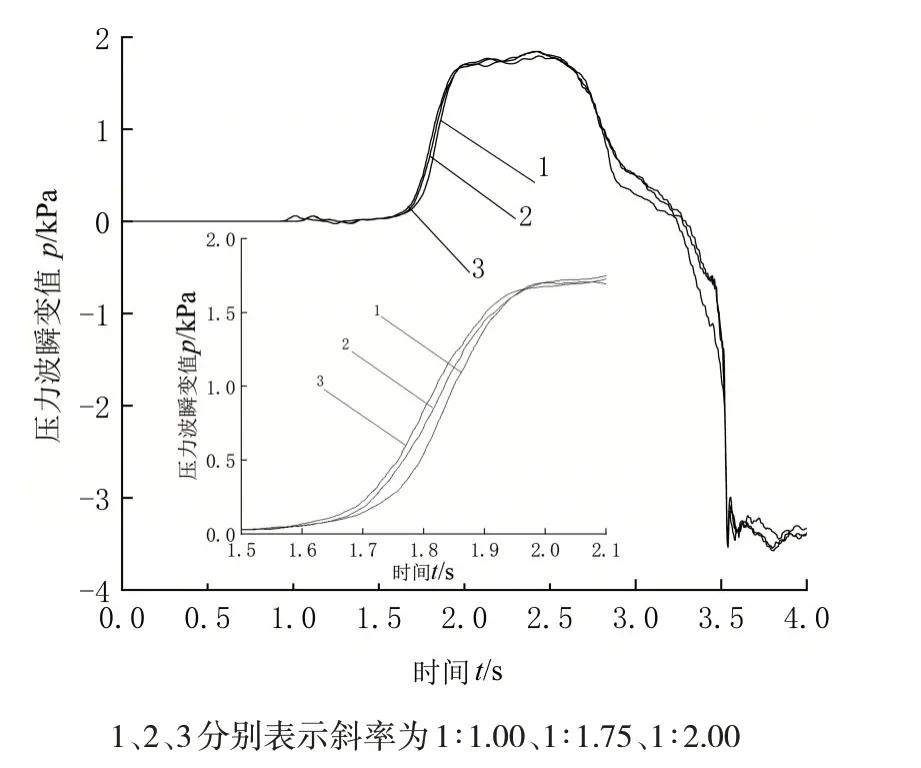
图3 不同洞门斜切斜率时隧道中点压力波比较

综上所述，当高速列车驶入隧道过程中，改变帽檐斜切式隧道洞门的斜切斜率对隧道中部压力波的变化规律和幅值变化基本无影响。

2.1.2 车速对隧道内压力波的影响

分别对高速列车以250 km/h、300 km/h 和350 km/h的速度驶入隧道过程的流场建立多组数值计算模型。图4 所示为不同车速进入隧道时，隧道中部监测点的压力波变化曲线对比。

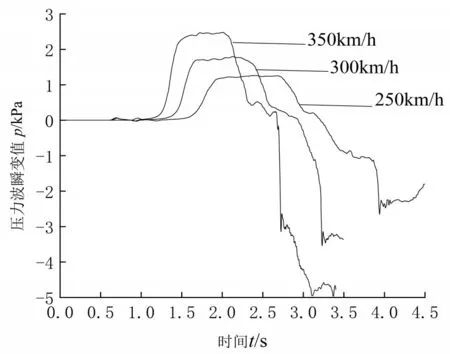
图4 不同车速下隧道中点压力波变化曲线

从图4 可以看出，隧道中部监测点的压力波在不同车速下的变化趋势基本一致，即在列车驶入隧道时该监测点压力开始波动并迅速上升，在这个过程中由于隧道壁面和车体壁面对空气的摩擦作用增加，导致该处压力在突增后变成逐渐升高直至列车车尾驶进隧道，同时车尾处产生的膨胀波也传播到此处，从而该处压力开始急剧下降。而该监测点的初始压缩波幅值随车速增大而增大。

为了研究压力波幅值与车速的关系，表1 记录了不同车速下隧道中部监测点的初始压缩波峰值和最大负压值。将表1 中数据生成拟合曲线，如图5（a）所示。表2记录了不同车速下隧道中部监测点初始压缩波梯度的最大值。将表2中数据生成拟合曲线，如图5（b）所示。

表1 不同车速下隧道中点压力波最大值比较

表2 不同车速下隧道中点初始压缩波最大梯度值

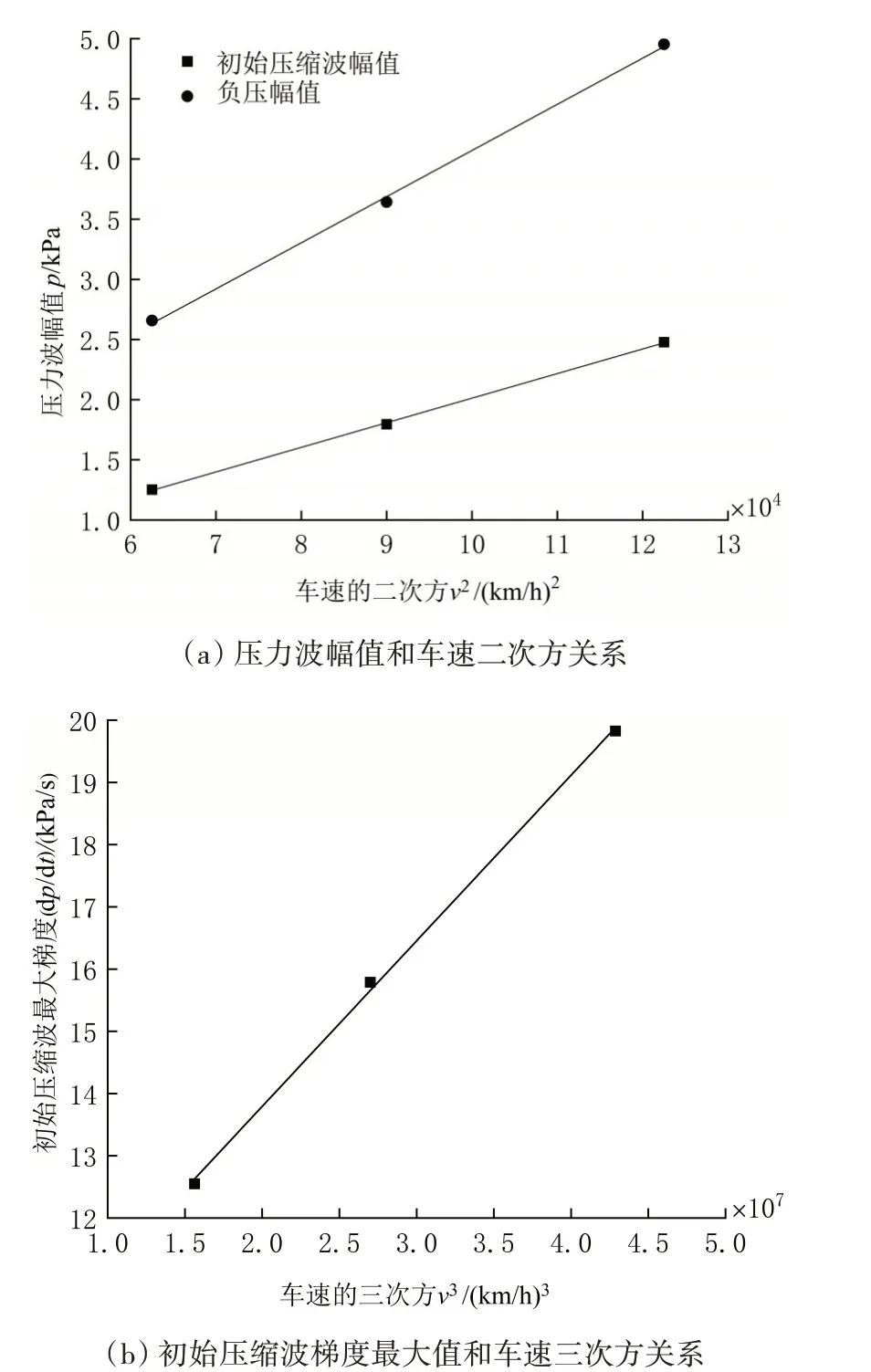
图5 压力波幅值和初始压缩波梯度最大值与车速关系

从图5（a）可以看出，隧道中部监测点初始压缩波幅值和负压幅值与车速的二次方成正相关。从图5（b）可知，该监测点的初始压缩波梯度峰值与车速的三次方成正相关。

综上所述，高速列车以不同车速驶入隧道过程中，隧道中部监测点的压力波变化趋势几乎相同且初始压缩波幅值随车速的增加而增加。隧道中部监测点的初始压缩波幅值和负压幅值与车速的二次方成正相关；初始压缩波梯度最大值与车速的三次方成正相关。

2.1.3 洞门斜切斜率对微压波的影响

微压波是高速列车隧道空气动力学的一种现象，其中含有大量低于10 Hz 的低频噪声，性质与次声波类似[21]。频率低于人听觉下限的微压波可能会造成隧道外建筑门窗的振动等不良影响。图6所示为列车以300 km/h 的车速通过隧道时，洞门斜切斜率对隧道出口约40 m 处微压波监测点的影响。表3记录了3种不同斜切斜率下微压波的幅值。在t=0 s时，列车处于初始位置。

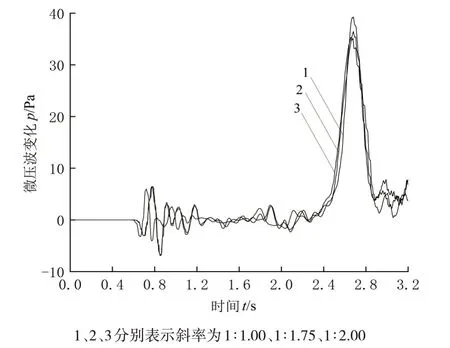
图6 隧道出口40 m处微压波随时间变化曲线

表3 不同洞门斜切斜率下微压波幅值

从图6 可以看出，列车在t= 1.08 s 驶入隧道时产生的压缩波在t= 2.34 s 时传到该监测点，导致该点压力开始迅速上升，在t= 2.66 s 左右列车头部完全进入隧道后达到最大值，之后开始急剧下降。同时还可以看出，随着洞门斜切斜率的减小，隧道外微压波监测点的压力幅值有所减小，但整体压力变化趋势没有变化。从表3 可知，洞门斜切斜率为1∶1.00时，该监测点的压力幅值最大，约为39.29 Pa，而洞门斜切斜率为1∶1.75 时为36.49 Pa，相较于斜切斜率为1∶1.00 时，下降约7.1%，当洞门斜切斜率为1∶2.00 时，该监测点的压力幅值最小，约为35.33 Pa，相比于斜切斜率为1∶1.00 时，降幅达10.1%。可见，减小隧道洞门斜切斜率可有效降低隧道外微压波强度。

综上所述，洞门斜切斜率的改变对隧道口微压波的变化趋势基本无影响，但可显著降低微压波幅值。

2.1.4 车速对微压波的影响

图7 所示为列车以250 km/h、300 km/h 和350 km/h 3 种不同车速通过洞门斜切斜率为1∶1.00的隧道时，距隧道口约40 m 处微压波的变化情况。t= 0 s 时，列车处于初始位置。表4 给出了不同车速下，距隧道出口40 m处微压波最大值。

图7 不同车速下隧道口微压波变化曲线

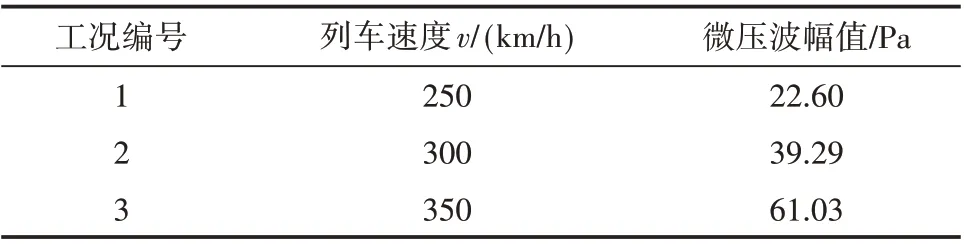
表4 不同车速隧道口微压波最大值对比

从图7 可以看出，不同车速下，距隧道出口约40 m 处的微压波变化趋势基本一致，且微压波幅值随着车速增加而增加。从表4 可知，当列车以350 km/h 的运行速度通过隧道时，隧道口外40 m 处的微压波幅值最大，约为61.03 Pa；车速为300 km/h时，压力波幅值次之，约为39.29 Pa。而当车速为250 km/h时，该处的微压波幅值最小，约为22.60 Pa，最大降幅达62.9%。可见，降低列车通过隧道的速度可大幅降低隧道口外的微压波强度。

综上所述，降低列车通过隧道的运行速度时，隧道口外微压波的变化趋势基本一致，而微压波幅值却大幅降低。

2.2 车头鼻尖处压力的变化

列车是长宽比很大且贴地运行的运输工具，当它驶过隧道时，列车车体表面将受到强烈的瞬态冲击，对车辆结构和使用寿命造成影响。本节取列车车头鼻尖处压力分布为研究对象分析车体表面的压力变化。

2.2.1 洞门斜切斜率对车头鼻尖处压力的影响

图8 所示为高速列车以300 km/h 的速度驶过3种不同洞门斜切斜率的隧道过程中对列车车头鼻尖处压力的影响；表5 列出了3 种斜切斜率下列车车头鼻尖处瞬变压力变化幅值。

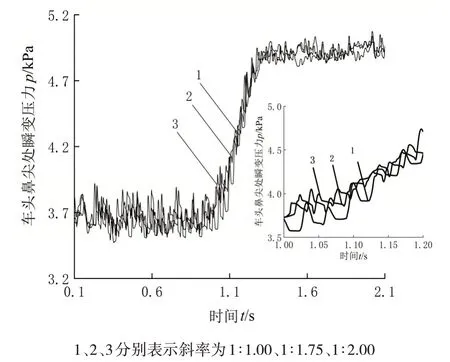
图8 列车车头鼻尖处瞬变压力比较

表5 不同斜切斜率下列车车头鼻尖处最大压力比较

从图8 可知，列车在不同洞门斜切斜率条件下驶过隧道过程中，车头鼻尖处瞬变压力变化趋势基本保持一致，即在t= 1.08 s 时，列车进入隧道缓冲结构时，车头鼻尖处压力迅速上升，到t= 2.08 s 时列车完全驶过隧道缓冲结构，车头鼻尖处压力在t=2.02 s时达到最大值。从表5可知，列车在不同洞门斜切斜率条件下驶过隧道期间，车头鼻尖处最大瞬变压力幅值相差约1.6%，即车头鼻尖处最大瞬变压力幅值基本上不受洞门斜切斜率的影响。造成该现象的原因在于列车以相同速度驶入相同长度的隧道情况下，影响列车表面压力变化的最主要因素是阻塞比，而在本文的研究中，列车-隧道的阻塞比保持不变且帽檐斜切式洞门结构并不会改变阻塞比，因此改变洞门斜切斜率对车头鼻尖处的压力变化基本无影响。

综上所述，改变隧道洞门的斜切斜率对列车车头鼻尖处的压力变化趋势和最大值几乎无影响。

2.2.2 车速对车头鼻尖处压力的影响

在高速列车以250 km/h、300 km/h 和350 km/h 3 种运行速度驶过隧道过程模拟中，监测了高速列车车头鼻尖处压力变化，如图9所示。表6列出了不同车速下列车车头鼻尖处最大瞬变压力值。在t= 0 s时，列车处于初始位置。

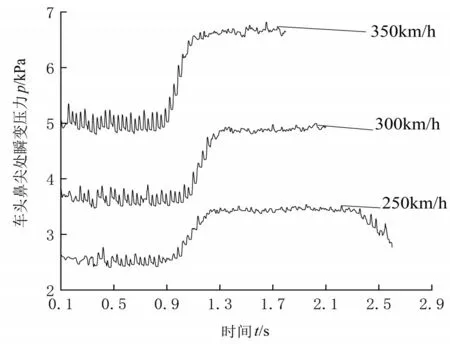
图9 不同车速下列车车头鼻尖处瞬变压力变化

表6 不同车速下列车车头鼻尖处最大压力比较

从图9 可以看出，高速列车以不同速度从明线驶入隧道过程中，列车车头鼻尖处的压力变化趋势几乎相同。从图9和表6可知，列车车头鼻尖处压力最大值随列车运行速度增加而增大。为了得到车速与列车车头鼻尖处压力幅值的关系，将表6 中不同列车速度的列车车头鼻尖处压力最大值数据生成拟合曲线，如图10 所示。从图10 可以看出，列车车头鼻尖处的压力幅值与车速的二次方成正相关。

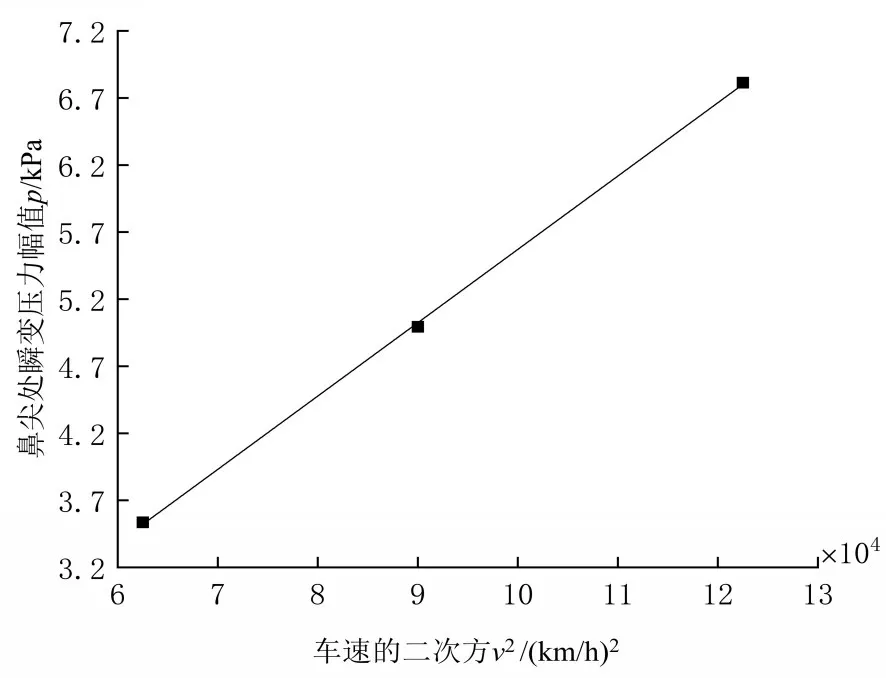
图10 列车车头鼻尖处最大压力与车速关系

综上所述，高速列车以不同速度驶入隧道时，列车车头鼻尖处压力变化趋势基本相同且最大值随车速增加而增加，其值与车速的二次方成正相关。

3 结 论

基于RNGk-ε 双方程湍流模型，通过对高速列车驶过帽檐斜切式隧道的气动性能模拟研究，得出以下结论：

（1）隧道洞门斜切斜率的改变对隧道中点压力波的变化趋势和最大值几乎无影响。

（2）在不同列车运行速度条件下，隧道中点压力波的变化趋势基本一致且压力波最大值随车速增加而增大。通过对数据拟合可知，初始压缩波幅值和负压幅值与车速的二次方成正相关；初始压缩波的瞬变压力梯度幅值与车速的三次方成正相关。

（3）洞门斜切斜率和车速的减小不会改变隧道口外的微压波变化趋势，但可显著降低微压波幅值。

（4）改变隧道洞门斜切斜率，对列车车头鼻尖处的压力变化趋势和最大值几乎无影响。而列车车头鼻尖处的压力随车速的增加而增加，且其压力幅值与车速的二次方成正相关。