不同郁闭度天山云杉林分形维数特征

马琪瑶，王振锡，曲延斌，葛 瑶，吕金城，郝康迪，董 巍

（1. 新疆农业大学 林学与风景园林学院，新疆 乌鲁木齐 830052；2. 新疆维吾尔自治区教育厅干旱区林业生态与产业技术重点实验室，新疆 乌鲁木齐 830052）

分形理论最早由美国数学家Mandelbrot 提出，用来描述不规则、甚至不能作为经典几何研究对象的自然事物，试图透过混乱现象和不规则构型揭示隐藏于现象背后的局部与整体的本质联系和运动规律[1-2]。分形定义为部分与整体具有某种形式相似的形体，即具有自相似性的形体，用来描述自然界中具有自相似性的粗糙或零碎的形体[3]。其对物体的描述更加符合自然事物的复杂性、多样性及不规则性。在自然界中，不同的地物具有不同的分形特征。现今分形理论已应用于生态学[4-6]、地质学[7-8]、自然地理学[9-10]等多个领域。

分形理论在林业中较多应用于树木冠层和根系分形特征的研究。如马良清等[11]以沙漠成年沙枣树为研究对象，运用分形理论和方法，得出沙枣的叶片分维数、树冠分维数、整株分维数，不仅反映了沙枣生存环境之间的联系，还填补了经典测树学之不足。董春胜等[12]采用分形盒维数方法测定植物根系维数，发现樟子松生长到约15 a时，根系维数变化基本稳定。除此之外，还有关于白杨[13]、黄金树[14]、红海榄树[15]等冠层或根系分形特征的研究。随着遥感技术的快速发展，尤其是无人机遥感以其超高分辨率的优势，在林业调查方面表现出很强的生命力[16-17]。遥感图像提供了大范围的区域图形，有很强的综合性，宏观反映了地物的分布和形态，而每一种地物本身具有自身的分形特征，所以为地物的分形特征研究提供了技术途径，同时也为分形理论与森林资源调查的结合提供了有利条件。前人在土地应用分类[18]、遥感图像分类[19]等方面的研究也表明分形维数参与分类能够提高分类的精度。新疆山地森林中分布最广、蓄积量最大的优势树种是天山云杉Picea schrenkianavar.tianschanica，其主要分布在天山北坡，天山南坡和昆仑山西部北坡也有少量分布。天山云杉林以纯林为主，是构成天山乃至新疆森林生态系统的物质主体[20]。以天山云杉为主体的天山山地森林生态系统在水源涵养、水土保持及林区生态系统的形成和维护等方面发挥着重要作用[21]。林分郁闭度在林分调查因子中是常用来表达林分密度的指标，反映林分结构和环境的重要因子。通过郁闭度能反映林分的光能利用以及林分植被的生长情况[22]，它的大小影响着林下物种的多样性[23]，同样也影响着天山云杉林的生长。天山云杉主要分布在阴坡，窄冠塔形树冠，在遥感图像上具有很强的纹理特征，这种分布特征和树型特征表现出明显的自然属性特征，非常适合用分形维数来度量。

基于此，本研究以无人机遥感影像为数据源，以新疆农业大学实习林场的天山云杉林为研究对象，探究不同郁闭度下天山云杉林的分形维数特征，以期为新疆山区天然林森林分类提供新的思路。

1 研究区概况

研究区位于天山山脉中段的新疆农业大学实习林场—天格尔森林公园（地理坐标为43°16′ ～43°26′N、86°46′ ～86°57′E），地 处 头屯河上游，乌鲁木齐县境内。研究区属温带大陆性气候，平均年降水量约600 mm，其中7 月相对湿度可达65%，年平均温度3℃，年日照时数为1 300 h，海拔为1 700 ～3 200 m，由南到北呈降低的趋势，坡度多在10°～40°之间。研究区内以天山云杉林纯林为主，林下土壤基本为灰褐色森林土。主要乔木树种为天山云杉，主要草本为老鹳草Geranium wilfordii、林地早熟禾Poa nemoralis、紫苞鸾尾Iris ruthenica、黑穗笞草Carex atrata等。

2 研究方法

2.1 数据来源

2.1.1 影像数据

研究区无人机图像数据由SONY DSC-RX1R2相机拍摄，该相机具有35 mm 的定焦镜头，图像有效像素为4 200 万。2019 年8 月15 日，天气晴朗，能见度高，根据预先设定的航向、航线和高度对研究区进行航拍，航拍图像航向重叠为80%，旁向重叠为60%，飞行高度为1 000 m，获取的无人机影像地面分辨率为0.1 m。

2.1.2 外业调查数据

在新疆农业大学实习林场天山云杉林区域选取典型样方，样方规格为30 m×30 m，依据郁闭度差异共选取60 个样方，采用对角线法测定样方郁闭度，疏郁闭度（0.20 ～0.39）、中郁闭度（0.49 ～0.59）、密郁闭度（0.60 以上）样方数量分别为20、20、20。

2.2 分形维数的计算方法

分形维数是表征自相似结构的指标之一，是定量描述分形特征的重要参数[24-25]。计算分形维数的方法一般有盒子数、分形布朗运动、双毯覆盖模型、频域法等。其中盒子维计算方法中的计数盒维是将覆盖图像表面所需的最小盒子数目作为对图像表面的一个度量，因其简便易行而得到了广泛的应用[26]。以计数盒维为基础，同时又有许多的改良算法，如差分盒子维（Differential box counting，DBC）和像素点覆盖法等。

2.2.1 像素点覆盖法

将图像进行灰度处理后，转换为二值化图像，图像矩阵中数值取0 或1，然后把矩阵用大小为g×g（g=1，2，4，…，2i）的小盒子进行覆盖，则图像中覆盖1 的小盒子数为ng，每个小盒子的边长为gδ=gδ(δ=l/m，l为图像边长，m为一行中像素点个数）[27]，在双对数坐标系中拟合数据点，则直线的斜率近似为盒维数。

2.2.2 差分盒子维

将K×K大小的图像划分为多个r×r子块，将其扩展到三维空间（x，y，z），（x，y）代表在三维空间的位置，z代表灰度值。假设在第（i，j）网格中的图像灰度的最小和最大值分别落在第n和第1个盒子中，则覆盖此网格所需盒子数（nr）为：

本研究采用MATLAB 软件计算天山云杉林的像素盒子维数和差分盒子维数。

3 结果与分析

3.1 图像处理

在ArcGIS 10.4 软件中对60 个不同郁闭度的典型样地（图1）无人机图像进行图像深度处理，把图像深度转换为unit 8（图2）。

图1 不同郁闭度下天山云杉林典型样地Fig. 1 Typical plots with different canopy densities

图2 改变影像深度后不同郁闭度林分典型样地Fig. 2 Typical plots with different canopy densities by changing image depth

对不同郁闭度典型天山云杉林样方的无人机影像进行灰度、二值化和二值化求反后，结果见图3。由于样地图像存在二值化处理后图像背景变成黑色，天山云杉变为白色，这时所计算的分形维数为图像背景的分形维数，所以需要对图像进行二值化求反，从而得到计算天山云杉分形维数的图像。

图3 MATLAB 处理后的图像Fig. 3 Images processed by MATLAB

3.2 盒子维数的计算

3.2.1 像素点覆盖法

采用像素点覆盖法，应用MATLAB R 2014 b软件及其插件Fraclab 2.2 计算不同郁闭度下天山云杉林的盒子维数，结果见表1。

通过对不同郁闭度天山云杉分形维数描述性统计（表2）得出，疏、中、密3 种不同郁闭度林分的天山云杉样方的平均像素点盒子维数分别为1.623 0、1.631 3、1.643 1，但也存在个别样方的值与分形维数平均值差异较大，如疏郁闭度林分中的14、44 和50 号样方的像素点盒子维分别为1.726 3、1.783 4 和1.721 5，郁闭度等级为密的38号样方像素点盒子维数为1.499 4（表1），但绝大部分样方像素点盒子维的值处于均值附近。疏郁闭度林分样方的分形维数的最大值与最小值分别为1.783 4 和1.480 7；中郁闭度林分天山云杉的分形维数的最大值为1.774 3，最小值为1.513 2；郁闭度等级为密的天山云杉样方的最大分形维数为1.798 0，分形维数的最小值为1.499 4。3 种郁闭度林分条件下天山云杉林分形维数的变异系数相差不大，中郁闭度林分中样方的分形维数的变异系数值最小，为0.044 2；郁闭度为密和疏的样方变异系数为0.048 7 和0.048 6，两者与中郁闭度林分中样方的变异系数相差0.004 5 和0.004 4，而两者之间的变异系数相差0.000 1。另外对数据进行方差分析，P=0.711 8 ＞0.05，表明数据间没有显著性差异（表3）。因此可以看出，不同郁闭度下天山云杉林的像素点盒子维数变异不大，基本处于稳定。

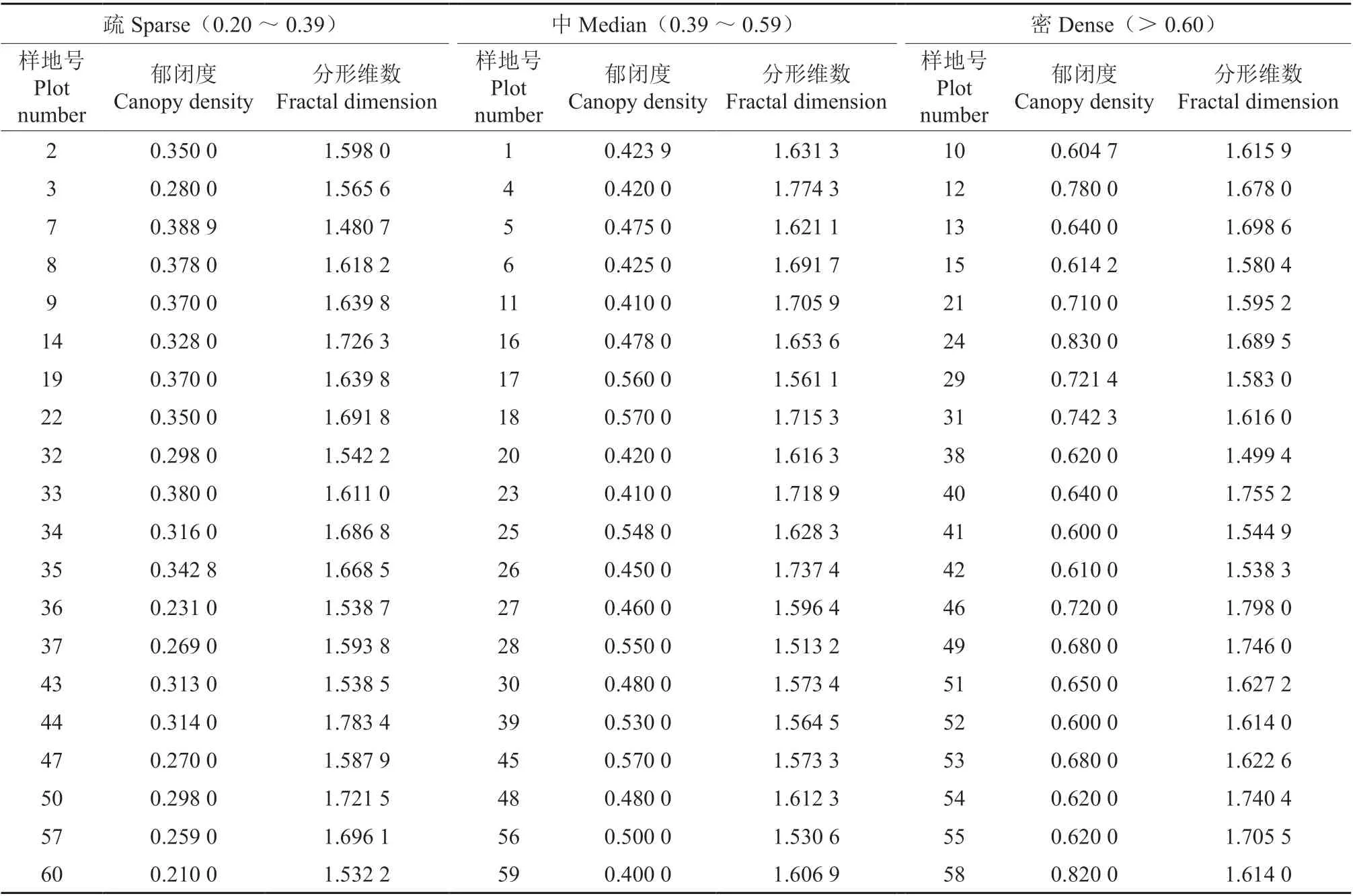
表1 不同郁闭度下天山云杉林像素点盒子维Table 1 Box dimensions of pixels in Picea schrenkiana var. tianschanica forests with different canopy densities

表2 不同郁闭度下天山云杉林像素点盒子维描述统计Table 2 Box dimension description statistics of pixels in Picea schrenkiana var. tianschanica forests with different canopy densities

表3 单因素方差分析Table 3 Single factor analysis of variance

由图4 可以看出，在不同郁闭度林分下，天山云杉林的像素点盒子维数随着样方郁闭度的增长而基本维持在稳定状态。像素点盒子维与郁闭度拟合直线的决定系数为0.008 8，远小于1，说明其分形维数在不同郁闭度下具有一定的稳定性。

图4 像素点盒子维与郁闭度的关系Fig. 4 Relationship between box dimension and canopy density of pixels

3.2.2 差分盒子维

在MATLAB 软件中对不同郁闭度的天山云杉林典型样地进行差分盒子维数计算，结果见表4。

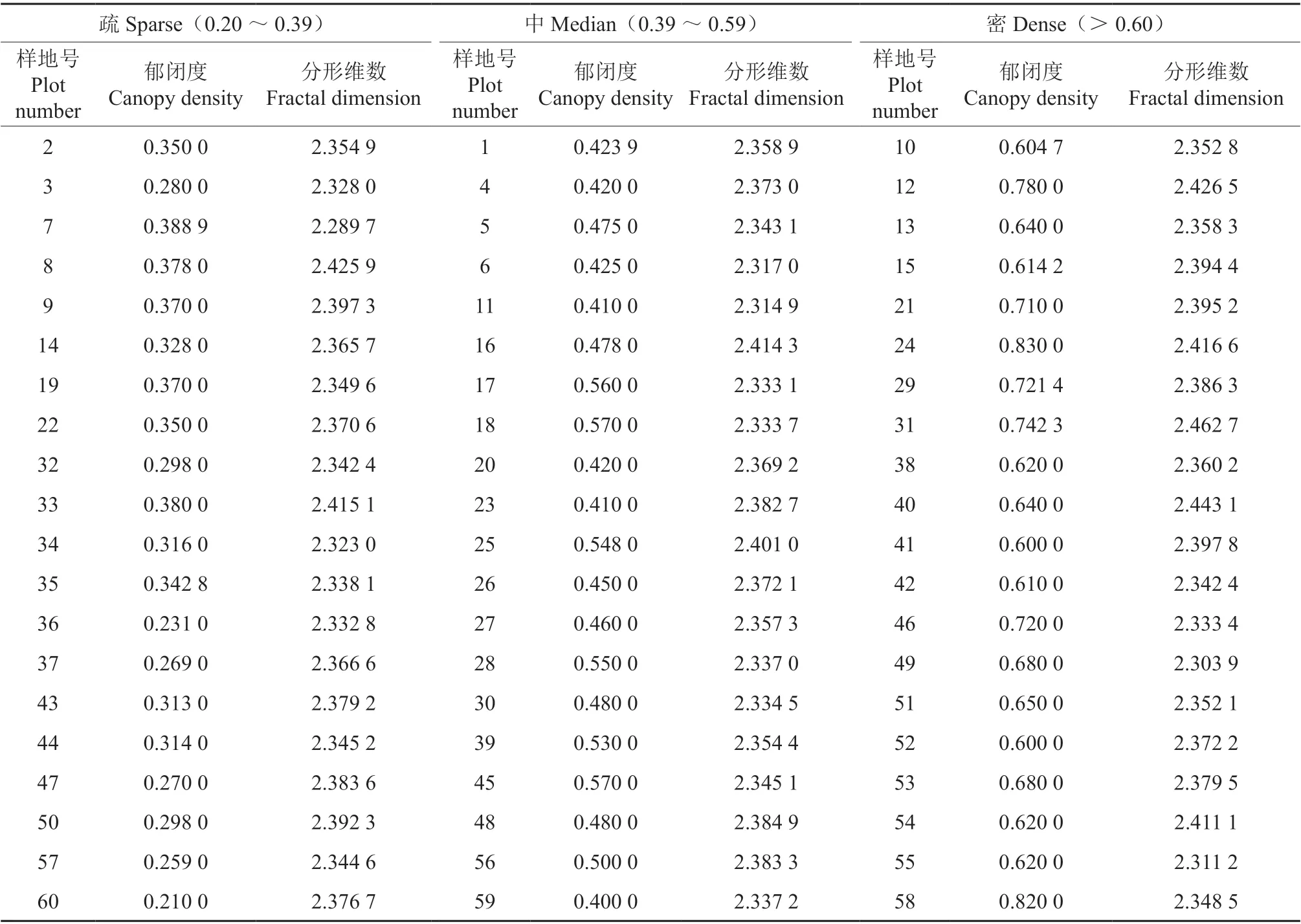
表4 不同郁闭度下天山云杉林的差分盒子维数Table 4 Difference box dimensions of Picea schrenkiana var. tianschanica forests with different canopy densities

通过对天山云杉林样方的差分盒子维进行描述统计（表5）得到，中郁闭度林分的样方差分盒子维的变异系数最小，为0.011 6；郁闭度为密的林分样方差分盒子维变异系数最大，变异值为0.017 7；疏郁闭度林分的样方差分盒子维的变异值为0.014 0。在疏、中、密3 种不同郁闭度林分下的样方平均差分盒子维数分别为2.361 1、2.357 3和2.377 4，两两之间差值处于0.01 ～0.03 之间；同时在选取的60 个典型样方中差分盒子维的最大值为2.462 7，最小值为2.289 7，相差为0.173 0。对数据进行单因素方差分析（表6）得出，P=0.158 2 ＞0.05，说明数据之间不存在显著性差异，即不同郁闭度条件下天山云杉林的差分盒子维数较为稳定。

表5 不同郁闭度下天山云杉林差分盒子维描述统计Table 5 Difference box dimension statistics of Picea schrenkiana var. tianschanica forests with different canopy densities

表6 单因素方差分析Table 6 Single factor analysis of variance

由图5 可以看出，随着郁闭度的升高，天山云杉林的差分盒子维数基本处于稳定状态。郁闭度与差分盒子维拟合直线的决定系数R2为0.058 9，远小于1，表明差分盒子维数与郁闭度的相关性极小，即样方的差分盒子维基本稳定。

图5 差分盒子维与郁闭度的关系Fig. 5 The relationship between difference box dimension and canopy density

4 结论与讨论

本研究采用无人机航拍图像数据，与传统森林资源调查使用的中高分辨率遥感数据相比，图像分辨率更高，细节信息更为清晰。另外，本研究所使用的无人机影像在夏季太阳高度角最大时拍摄，具有可见度高、没有冬季积雪干扰、且树体阴影较少的特点，有利于分形维数的计算。

1）图像阴影对计算结果有一定的影响。在不同郁闭度的样方影像中，极少数样方影像在一定程度上存在阴影，在载入影像计算分形维数时，由于这些阴影的干扰，在一定程度上影响了天山云杉林分形维数数值大小。在计算像素点盒子维数时，载入图像经灰度和二值化处理后，出现了个别分形维数偏离均值较大的情况。这主要是由于将草地、空地同天山云杉归为一类，从而使分形维数出现了一定的偏差。但这种情况仅出现在个别样方，大部分样方的像素点盒子维数还是比较稳定的。

2）像素点覆盖法和差分盒子维。像素点覆盖法计算的是二维平面内的分维曲线，维度一般在1 ～2 之间，盒维数计算较精确，但人为划分不均，容易引起奇异变形从而产生误差[27]。而差分盒子维是将图像作为一个三维曲面，以灰度为z轴，其维度一般在2 ～3 之间，一般多用于可以作为图像表面纹理粗糙程度的度量，如葛丽娟等[28]以青海云杉树冠为研究对象计算其分形维数，发现不同海拔梯度下径级相同时，中海拔地区青海云杉冠层分形维数最大；相同海拔不同径级的青海云杉，随着径级的增大（除10 ～20 cm），树冠的分形维数呈减小趋势。本研究应用像素点覆盖法得到的不同林分郁闭度下天山云杉林分形维数基本处于1.623 0 ～1.641 3 之间，不同郁闭度下差分盒子维法得到的天山云杉林分形维数基本处于2.361 1 ～2.377 4 之间，两种方法得到的分形维数的浮动范围均小于0.02。即在不同林分郁闭度条件下，无论是像素点覆盖法还是差分盒子维得到的天山云杉林分形维数都基本处于稳定状态，说明在不同林分郁闭度条件下天山云杉林具有稳定的分形特征。

3）变异系数可以表征天山云杉林样方的分形维数的离散程度，本研究中，像素点覆盖法的变异系数为0.047 2，差分盒子维法的变异系数为0.014 9，差分盒子维法的变异系数小于像素点覆盖法的变异系数，即差分盒子维法计算的样方分形维数的离散程度小，稳定性较高。

本研究基于分形理论，分别采用像素点覆盖法和差分盒子维法计算了不同郁闭度下天山云杉林的分形维数。当采用像素点覆盖法时，天山云杉林的分形维数基本保持稳定，不随郁闭度的变化而变化；当采用差分盒子维法时，天山云杉林分形维数表现为稳定状态，不随郁闭度变化而变化。可见，不论采用哪种方法计算分形维数，天山云杉林的分形维数都处于较为稳定的状态，即不同林分郁闭度下天山云杉林具有稳定的分形特征。而从分形维数的离散程度分析，差分盒子维法计算天山云杉林分形维数优于像素点覆盖法。

本研究利用分形维数来表征天山云杉林的分形特征，从一个新的角度研究天山云杉林的基本特征，为今后天山云杉林基本特征及森林分类区划等方面的研究提供了新的思路。如徐文海[19]基于分形理论对TM 影像纹理特征进行提取，发现其有助于提高遥感影像非监督分类的精度。但本研究仅从林分的郁闭度出发，研究天山云杉林的分形维数，没有综合考虑地形因素（坡度、海拔、坡向等）对天山云杉林分形维数的影响。因此，在今后研究天山云杉林分形维数时，还需要综合考虑地形因素的影响，开展更深入的探讨和研究。