基于SPH的椭圆双极线性聚能药包控制爆破数值模拟研究

2022-07-20徐世祥黄宗辉

煤炭科学技术 2022年5期

吴波，韦汉，徐世祥，许杰，黄宗辉

(1.广西大学土木建筑工程学院，广西南宁 530004；2.教育部工程防灾与结构安全重点实验室，广西南宁 530004；3.广西防灾减灾与工程安全重点实验室，广西南宁 530004)

0 引言

聚能装药广泛应用于军事领域，比如爆炸成型弹丸、破甲弹设计等，此外聚能装药也被广泛应用于工业生产，尤其是在实现岩石的定向断裂控制爆破技术中。线性聚能装药是通过挤压聚能药型罩形成聚能射流的，从而达到定向断裂控制爆破的效果。近年来，人们对线性聚能装药爆破技术进行了广泛的研究，由于爆破的瞬时性，实验和理论难以捕捉爆炸的整个过程，而数值模拟可以再现爆炸的过程，使之成为续实验和理论之后的一种研究手段。MOLINARI[1]采用有限元来研究聚能装药中铜射流的形成、破碎和侵彻过程。王成等[2]通过ALE研究不同起爆方式对线性聚能射流形成的影响进行分析。张先锋等[3]也通过ALE对3种不同典型线性装药的聚能射流形成及侵彻过程进行了数值模拟。李必红[4]从理论、实验与数值模拟研究椭圆双极线性聚能药包的爆破机理，提出了有效装药边界函数并通过理论推导确定。

以上实现的数值分析都是基于网格的拉格朗日方法、欧拉方法或者两者的结合，然而实现的拉格朗日方法由于大变形的存在往往使得计算终止，而欧拉方法或ALE方法对物质边界的捕捉存在一定的困难。由于无网格法具有处理大变形和破坏问题的特点，使得其成为处理极端变形条件下有限元无法比拟的优势，尤其是无网格SPH方法在线性聚能装药中的应用。SPH方法最早于1977年由LUCY等[5]提出并将其天体物理学，随后广泛应用于各个领域的研究，SWEGLE等[6]首次将其应用于水下爆炸数值研究，实现SPH在爆炸领域的应用，LIU等[7-8]等基于SPH对无药型罩聚能装药爆轰过程及聚能射流形成过程进行研究。YANG等[9]基于二维模型对线性聚能射流进行SPH模拟研究，并对比分析不同数值分析方法对聚能射流的影响。李磊等[10-11]通过SPH实现聚能装药的三维数值模拟，并将SPH方法与有限元耦合实现聚能射流对钢板的侵彻效果。杨建辉[12]通过SNSYS/LS-DYNA对切缝聚能管参数进行优化，分析不同参数下对岩石应力状态的影响。陈帅志等[13]基于LS-DYNA分析切缝药包与普通药包爆炸在岩石的传播特性。岳中文等[14]结合数值模拟及试验研究炮孔间距对切缝药包爆破引起的裂纹扩展的影响。张盛等[15]将椭圆双极线性聚能药包在巷道中的应用，并结合现场试验对参数进行优化研究。

综上所述，目前对聚能装药形成数值分析主要基于有限元分析，而有限元模型无法动态捕捉爆生气体跟聚能罩的动态演化规律，或对带聚能槽的矩形药包或切缝药包进行聚能分析，而基于无网格实现椭圆双极线性聚能装药结构的研究较少。鉴于SPH方法在处理爆炸这种极端变形等复杂条件下具有有限元无法比拟的优势。笔者基于SPH方法研究聚能装药的形成，并与已有试验及模拟做对比，验证本文实现的SPH方法的有效性；然后基于SPH研究椭圆双极线性聚能药包爆破机理并分析外壳及其厚度、药型罩及其厚度对椭圆双极线性聚能药包实现聚能射流及其对岩石定向断裂控制爆破技术的影响。

1 SPH控制方程理论

SPH方法的核心思想就是通过构造一个核函数对粒子的核估计来计算梯度的相关量，不需要求解偏微分方程，而是将偏微分控制方程转化为积分形式，偏微分方程的转化包括函数核近似和粒子近似两步，函数核〈f(x)〉[11]近似如下：

(1)

式中，W(x-x′，h)为光滑函数或核函数;Ω为积分域；x为空间坐标；x′为x紧支域内某一点的坐标；h为光滑长度。

对于连续形式的核近似式，函数f(x)的粒子近似可对粒子i紧支域内所有粒子j进行加权求和[16]，即

(2)

式中：mj，ρj分别为粒子i的临近粒子j的质量和密度。

光滑函数需要满足归一化、δ函数性质和紧支性3个基本条件，常见的光滑函数有3次B样条函数、5次B样条函数、高斯核函数、指数核函数等，本文采用的是最常用的3次B样条核函数[11]，形式如下：

(3)

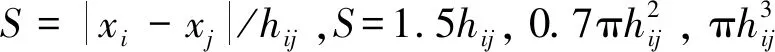
在粒子近似过程中，如果采用固定光滑长度，粒子集中时将影响计算效率，同时对于具有强度的材料可能造成张力不稳定的现象，粒子散射时会出现粒子紧支域内粒子数减少造成数值不稳定，因此本文采用变光滑长度法，其光滑长度的时间积分[17]格式如下：

(4)

式中:d为空间维数，本文取d=2；v为粒子速度；h(t)为粒子光滑长度；div为辅助函数。

2 模型验证

2.1 试验描述问题

通过选取与文献[18]相同的几何参数模型，模型参数分别为药型罩顶角W=80，厚度D=1.35 mm，装药长度L=25.4 mm，装药高度H=28.45 mm，模型如图1所示。通过LS-DYNA删除Lagrange单元信息再添加SPH相关属性，实现的SPH二维分析模型如图2所示。试验模型实现的SPH粒子间距为0.008～0.010 cm，炸药和药型罩的最小最大光滑长度分别为初始光滑长度的0.2倍和2倍，由于模型对称，计算时取1/2模型进行计算。

图1 数值模型Fig.1 Numerical model

图2 SPH离散模型Fig.2 SPH discrete model

炸药采用B炸药进行分析模拟，并采用MAT_HIGH_EXPLOSIVE_BURN模型描述材料本构，状态方程为JWL:

(5)

式中：p为爆轰压力；E为比内能；V为相对比容；A、B、R1、R2、ω为状态方程系数，炸药材料参数及状态方程参数见表1[18]。

表1 B炸药材料参数Table 1 B explosive material parameters

金属药型罩同样采用文献[18]的材料1006号钢，本构模型为MAT_JOHNSON_COOK模型，状态方程为EOS_GRUNEISEN：

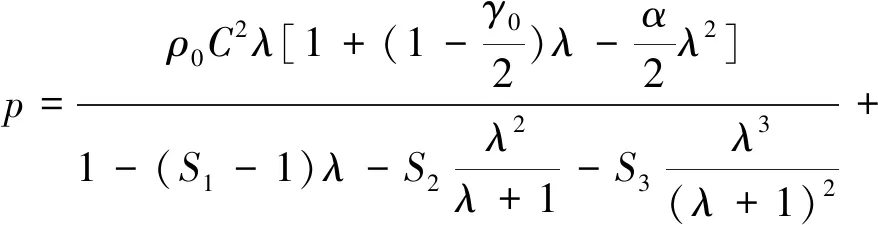
(6)

表2 1006号钢材料参数Table 2 Material parameters of No.1006 steel

2.2 模拟结果分析

图3为聚能射流形成过程中不同时刻射流形态及速度分布。由图3可知，基于LS-DYNA实现的SPH线性聚能射流与文献[18]基于高斯光滑核函数的自编程序实现的聚能射流在不同时刻基本一致，且都在t=4 μs 时爆轰基本完成，射流初步形成，如图3a所示。

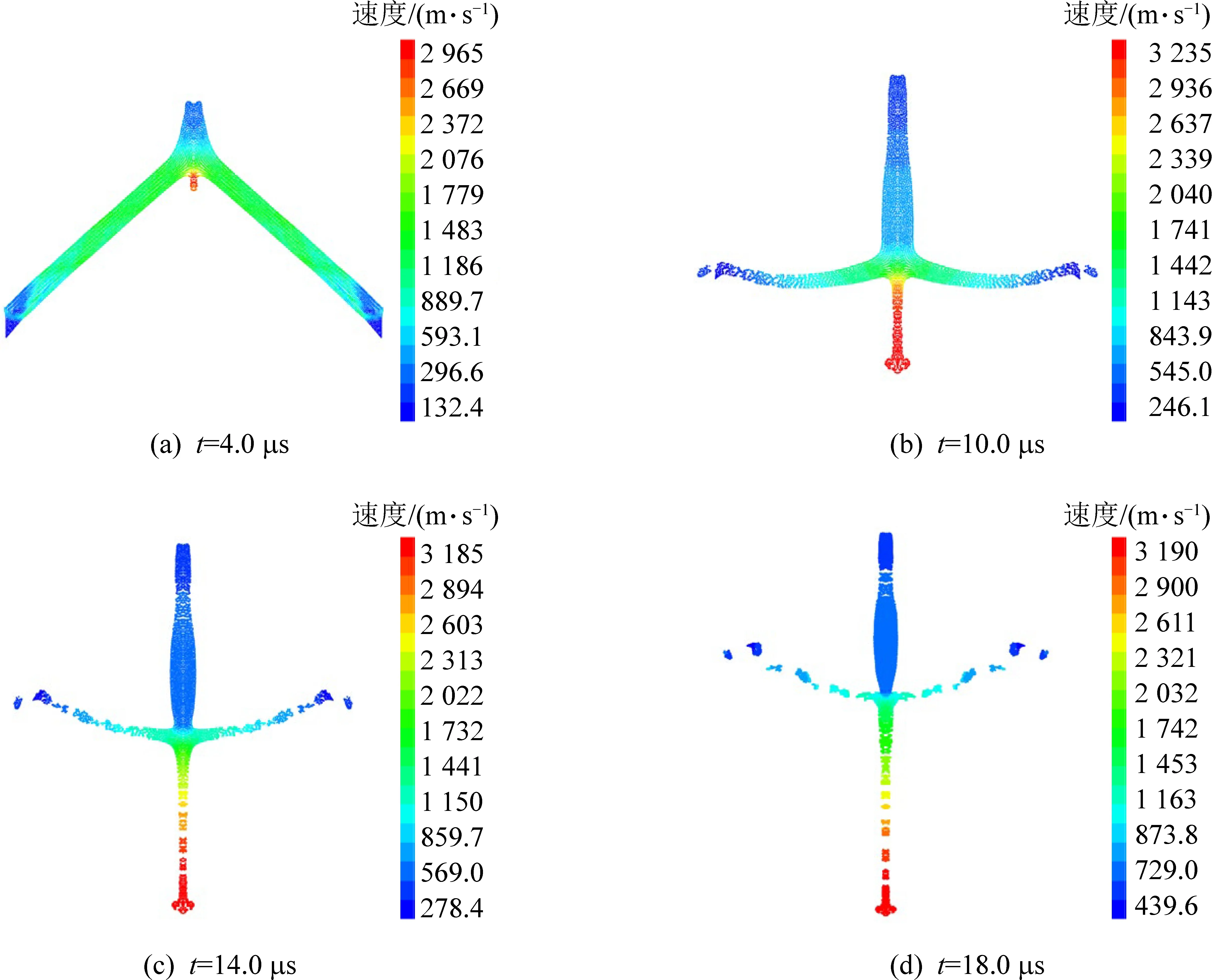
图3 聚能射流形成不同时刻速度云图Fig.3 Cloud chart of velocity at different time of jet formation

图4为t=6.5μs时聚能射流的速度云图，此刻射流头部平均最大速度达到3 507 m/s，与文献[19]电磁线圈测得射流头部最大平均速度值3 520 m/s基本一致。文献[18]实现的SPH方法获取的射流头部峰值速度为3 294 m/s，文献[19]通过X光技术测得的射流头部峰值速度为3 300～3 500 m/s，本文实现的SPH聚能射流形成稳定之后射流头部平均速度为3 180 m/s，说明本文实现的SPH方法和文献[18]及文献[19]基本一致，表明本文基于DYNA实现的SPH方法的有效性。

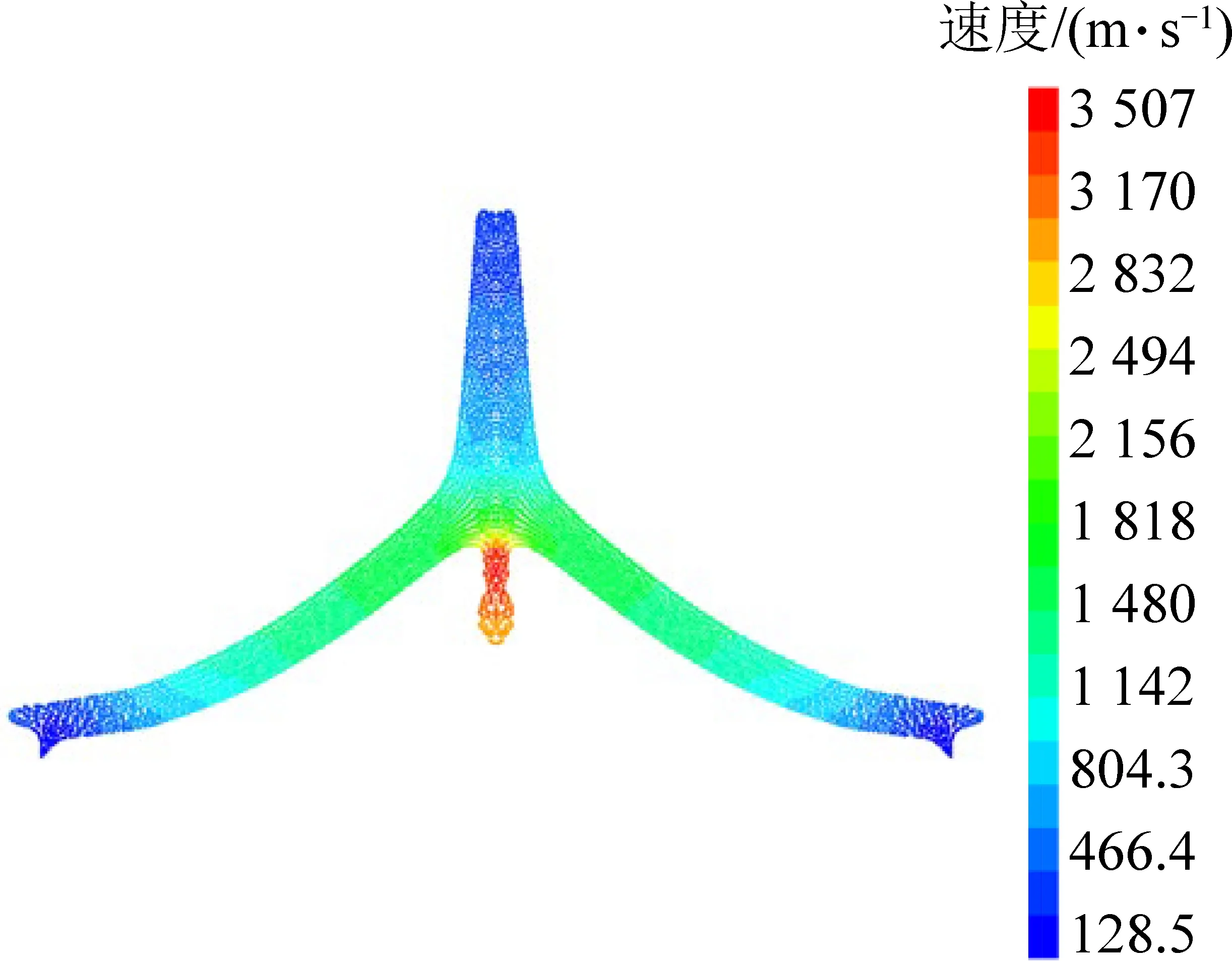
图4 t=6.5 μs时刻聚能射流速度云图Fig.4 Cloud chart of jet velocity at t=6.5 μs

3 椭圆双极线性聚能药包爆破数值分析

基于前文实现的SPH方法，可知SPH可以处理极端变形复杂条件下的破坏问题，为此对椭圆双极线性聚能药包爆破机理及其影响因素(外壳及其厚度、药型罩及其厚度)进行分析。

3.1 椭圆双极线性聚能药包形成

3.1.1 模型的建立

图5为椭圆双极线性聚能药包四分之一模型，几何参数如图5a所示,长短轴比为11∶15，离散模型如图5b所示，为考虑薄外壳与药型罩具有足够的临近粒子数，减小外壳与药型罩的粒子间距，考虑模型尺寸较小，将炸药粒子间距设置为外壳及药型罩相同的粒子间距0.008～0.010 cm。模型材料参数取值与上节材料参数一致，外壳选取与药型罩相同的材料及本构方程和状态方程。整个模型采用变光滑长度的计算方法，炸药、外壳和药型罩的最小最大光滑长度分别为初始光滑长度的0.2倍和2倍，计算时采用对称边界处理。

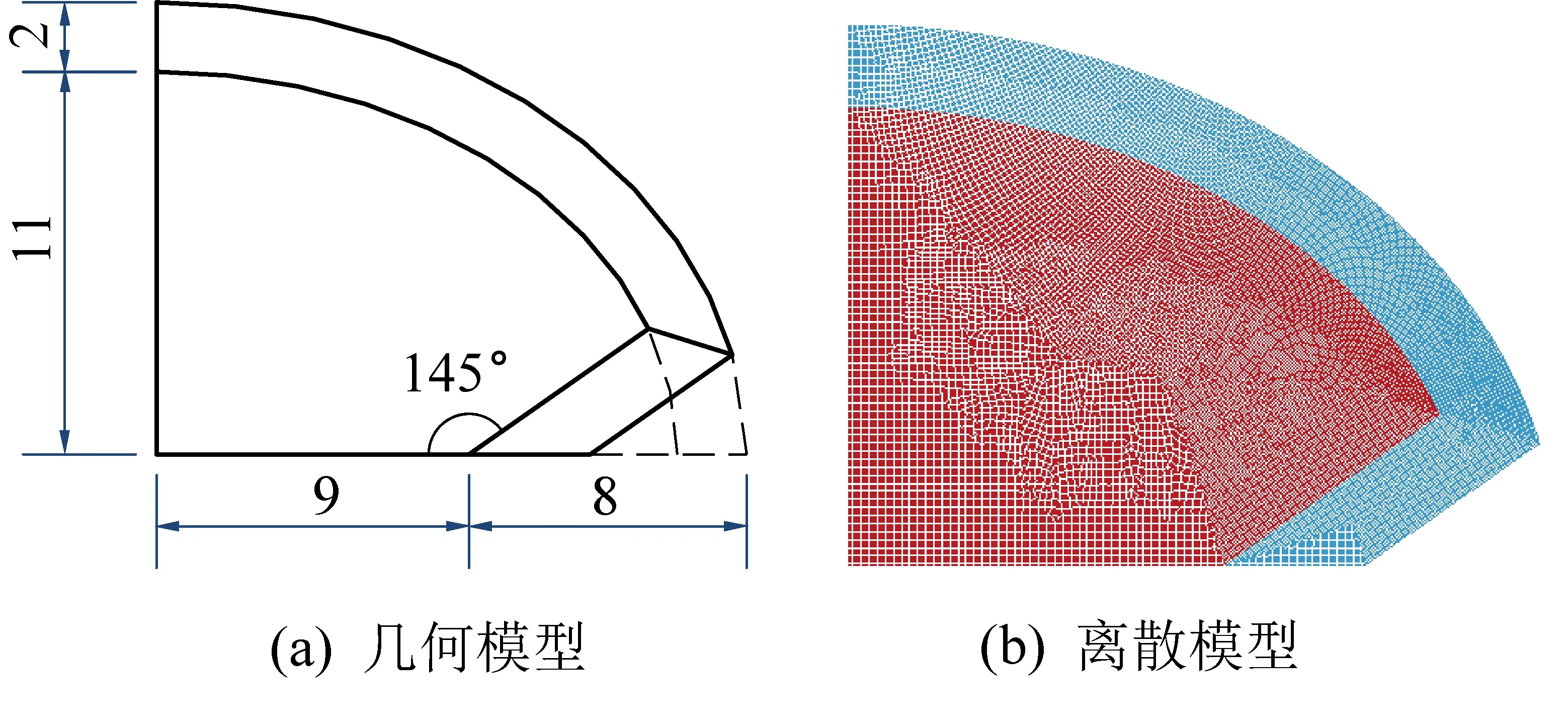
图5 四分之一聚能药包模型Fig.5 Quarter model of shaped-charge

3.1.2 聚能药包作用机理分析

图6为聚能射流形成不同时刻速度分布云图。t=0.8 μs时爆轰波先传到药型罩锥角顶端，开始挤压药型罩形成射流，随后到达90°非聚能方向的外壳，开始冲击作用于90°非聚能方向的外壳，使之开始发生压缩变形与向外运动。t=4.0 μs时射流初步形成，射流头部平均最大速度达到3 224 m/s，外壳不断发生塑性拉伸及向外运动，同时外壳与药型罩连接部位受拉力作用不断拉伸缩颈。在t=14.0 μs时连接部位首先发生断裂，爆生气体从该位置溢出，此时射流不断被拉伸，并与存在速度梯度的杵体部分逐步分离，由于射流不再受杵体、爆生气体和外壳的影响，射流头部平均速度基本保持不变。但最大速度并未发生在射流头部，而是在药型罩与外壳连接处的炸药粒子，由于射流形成稳定后不再受其他因素的影响，而接触部位炸药粒子在脱离药型罩与外壳的约束作用之后受到内部相邻炸药粒子的直接加速作用。t=20.0 μs时，脱离外壳与药型罩的炸药粒子不断加速追赶射流头部，此时炸药粒子最大速度达到3 772 m/s，而射流头部平均最大速度为2 985 m/s，同时在90°非聚能方向的外壳不断发生缩颈甚至断裂。

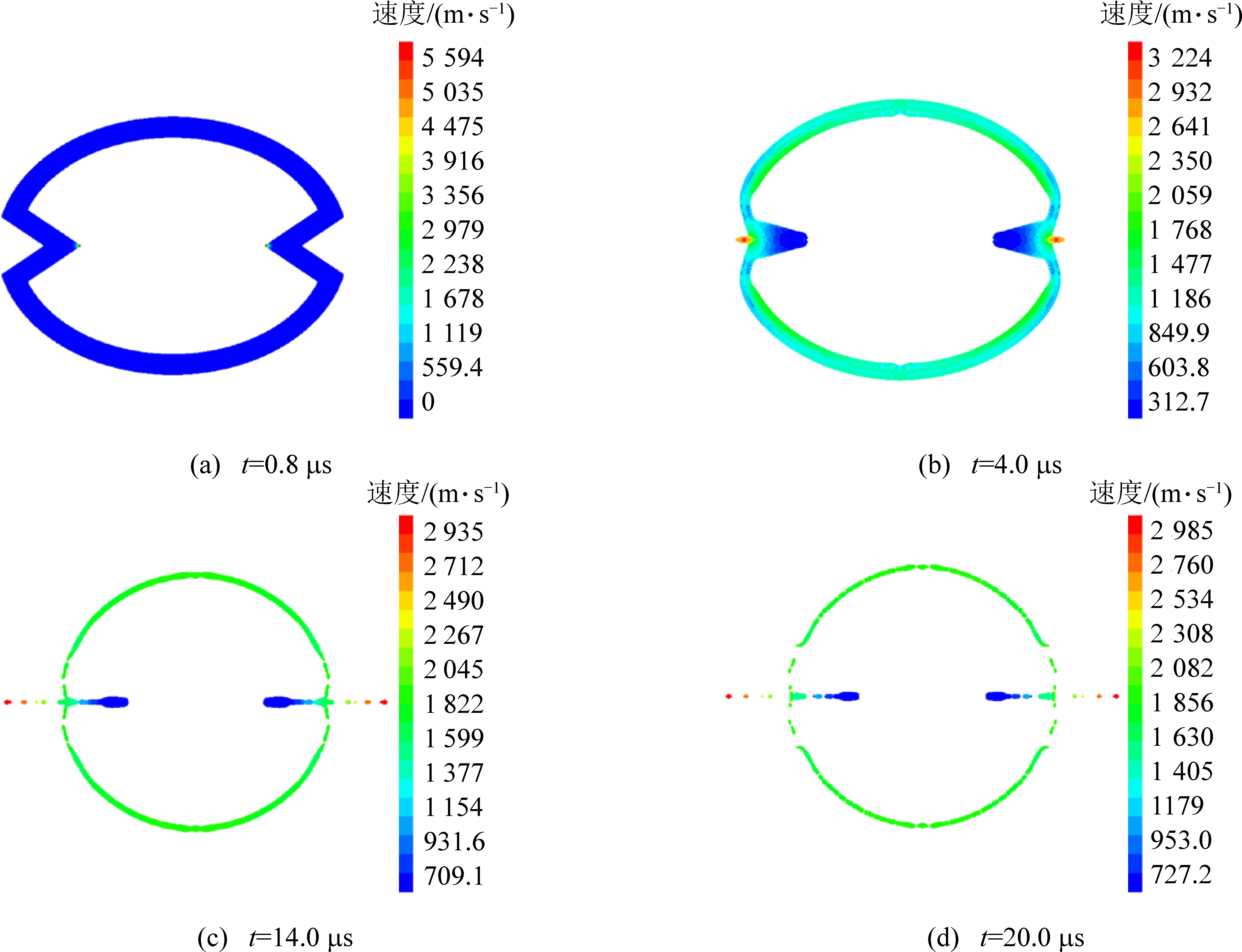
图6 聚能射流形成不同时刻速度分布云图Fig.6 Cloud chart of velocity distribution at different time of jet formation

图7为不同位置粒子的时间历程曲线，A′为射流头部粒子编号为302614，B′为药型罩与外壳接触部位内侧的炸药粒子编号为292551，C′为90°非聚能方向外壳粒子编号为302831，D′为90°非聚能方向外壳内侧炸药粒子编号为290904。由图可知，聚能射流在t=4 μs时射流基本形成，与图6b表述相吻合。t=14.0 μs时爆生气体溢出药型罩与外壳连接位置，最终在t=15.0 μs后粒子以3 440 m/s的速度稳定向前运动。90°非聚能方向外壳粒子与外壳内部炸药粒子的速度增加的总体趋势一致，但由于炸药粒子受到爆轰波的往复作用，速度波动幅度相对外壳粒子要大。此外，射流头部速度发展较快，其他粒子速度存在明显的时间滞后现象。

图7 不同位置处粒子速度随时间变化曲线Fig.7 Curve of particle velocity with time at different positions

3.2 聚能药包参数优化

3.2.1 问题描述

不同几何参数的椭圆双极线性聚能药包四分之一模型如图8所示，在保证长短轴比、聚能槽角度和装药量一致的情况下，各个模型采用相同的材料参数和粒子间距(同上节)。粒子的最大、最小光滑长度分别为0.2倍和2倍初始光滑长度，为保证初始时刻每个粒子的支持域内具有相同的质量，每个粒子初始临近粒子数设置为600。

图8 不同几何参数的聚能药包四分之一模型Fig.8 Quarter models of shaped-charge cartridge with different geometric parameters

3.2.2 数值模拟结果及分析

图9为不同几何参数聚能药包在t=14.0 μs时速度云图，由图可知不同几何参数的聚能药包实现的定向效果不同。图9a为2 mm厚的药型罩1 mm厚外壳的聚能药包速度分布图，由图可知除射流头部速度比较大之外，外壳向外运动的速度也较大，整体速度大于杵体速度，主要是由于外壳比较薄，爆生气体对外壳做的功大部分转化为外壳动能。对比图9b无外壳情况可知，图9a形成的射流速度较大且药型罩大部分的粒子形成射流，而图9b药型罩大部分粒子用于形成杵体，表明外壳对聚能射流的形成产生较大影响。图9c为1 mm厚药型罩和2 mm厚外壳的聚能药包速度分布图，对比图6c的2 mm厚药型罩情况可知，两者在同一时刻形成的射流形态相似，但前者形成的射流头部速度更大，射流头部平均最大速度达到3 670 m/s，更有利于岩石的侵彻作用。图9d由于无药型罩而无法形成射流，图中只给出爆生气体从外壳切缝处溢出形态，该形态与申涛等[20]基于ALE算法模拟切缝药包爆破相似，由图可见粒子散射比较明显，实现的定向效果不显著。图9e为1 mm厚药型罩和1 mm厚外壳的聚能药包速度分布图，对比图6c可知同样前者形成的射流更明显，速度更大，表明药型罩和外壳厚度同时减小时有利于聚能射流的形成。图9f为无外壳无药型罩药包的爆生气体速度分布图，由图可见，并未形成明显射流，可见外壳与药型罩对聚能射流的形成起决定作用。

图10为不同几何参数聚能药包射流头部速度随时间变化曲线，通过比较图5a、图8a和图8b所对应的曲线可知，随着外壳厚度不断减小，最终射流头部速度不断减小，但三者的速度变化趋势基本一致，再次表明外壳对椭圆双极线性聚能药包射流头部的形成有一定的影响，外壳越厚更有利于稳定爆轰作用，从而有利于射流的形成，射流速度越大；比较图5a、图8c所对应的曲线，可知当药型罩为1 mm，外壳2 mm时形成射流头部速度最大，最大值为3 700 m/s，而图8d由于无药型罩而无法形成聚能射流，对应图10的曲线只不过是聚能方向外壳边缘处粒子的速度时间历程曲线，表明药型罩对聚能射流的形成起决定性作用；对比图5a和图8e所对应的曲线图可知，随着药型罩和外壳厚度一致减小，聚能射流头部速度增大，但对比图9f可知当两者减小为0时不形成射流。对比图8d和图8f所对应的曲线，由于两者均没有药型罩，只能借助炸药粒子分析，由图可见，两者速度曲线重合，即最终稳定速度完全一致，表明当无药型罩时并没有明显的聚能效应。