基于激光扫描的机器人运动目标跟踪技术研究

黄 东，陈乐庚

(1. 桂林信息科技学院电子工程学院，广西 桂林 541004；2. 桂林电子科技大学电子工程与自动化学院，广西 桂林 541004)

1 引言

随着人们对高质量生活的不断追求，机器人技术已经从工业领域扩展到医疗、教育、勘测等领域。在实际生活中，移动机器人无处不在。现阶段，对机器人研究不只限于其自身特点，更要对如何解决生活中实际问题进行研究。机器人由先进智能系统组成，要实现其运动目标的跟踪，需要了解所处环境的真实信息。障碍检测是目标跟踪的关键内容，在传统算法中，因对环境的不确定性因素考虑不够，常常导致跟踪结果不准确。近年来，激光扫描以测距准确度高、实时性强等优势在机器人移动目标检测领域被广泛使用。

文献[1]提出基于感知代理与移动控制理论的移动目标跟踪方法。首先构建机器人的代理模型与感知目标跟踪模型，并提出分布式运动目标检测，该方法由估计部分与一致性部分构成，经过这两个阶段的处理，目标状态与协方差矩阵能够达成一致，该方法提高了预测能力；确保机器人可以接近运动目标，避免与障碍物发生碰撞，实现对目标的跟踪，但该方法对机器人目标运动速度设置较快，容易会出现跟踪丢失，导致跟踪精度较低。文献[2]提出利用图像特性为反馈的模糊控制策略，对运动目标进行跟踪。在三轴直角坐标系内，将机器人、摄像机与计算机做为基础，建立无标定视觉的跟踪系统，该系统的工作原理为，利用摄像机对图像信息进行采集，并经过定位处理，识别出运动目标与机器人的距离，并利用模糊控制系统控制机器人的运动状态及轨迹，实时对图像信息进行反馈，结合模糊推理规则，对系统误差修正，最终达到稳定跟踪的目的。但该方法对目标跟踪的速度较慢，导致跟踪效率较低。

基于上述方法中存在的问题，提出基于激光扫描的机器人运动目标跟踪技术。通过对坐标系分析建立机器人运动模型；再根据障碍物的状态，对运动目标进行检测，确定机器人与目标之间的合适距离，利用卡尔曼滤波获取目标运动矩阵，并对其进行跟踪。与传统方法相比本文方法通过对运动目标的多种处理，提升了运动目标控制的可靠性，提高了跟踪精准度及效率。

2 激光扫描的滤波设计

在激光扫描过程中存在噪声干扰因素，主要包括跟踪环境中光源和激光光源相互干扰，导致像素混合；另一方面，测量目标的发射率过小或入射角过大导致数据丢失；由于障碍物的遮挡，产生扫描盲区；激光扫描线存在间隙，导致部分区域无法扫描。在对机器人进行导航时，由于上述干扰因素的存在，导致避障检测不准确，所以需要对激光扫描的数据进行滤波处理[3，4]。

激光扫描测距信息主要表现为在全部极坐标测量方向上，邻近时间点的测量数据存在相关性，并且在同一组测量中，邻近扫描角度上的测量信息同样具有较大相关性。所以，利用在线滚动动态自适应滤波去除在避障检测中的干扰。采用极坐标呈现的激光扫描测距数据(ρi，j，λi，j)，构建以ρi，j为中心的3×3的信息分析窗口

(1)

式中，ρi，j代表扫描中心到第j个障碍物之间的距离，λi，j为第j个障碍物的扫描位置与主扫描位置的角度值，下标i为测距信息的采样时间点，j代表测距信息在同一在数据中的排列顺序。因此，在该窗口中存在的9个数据在时间与空间上具有相关性，利用下述公式计算ρi.j和其相邻的数据之差Δρmin

Δρmin=min{|ρi+t，j+s-ρi，j|

(2)

式中，t与s不能同时等于0，Δρmin为时间和空间上邻近数据的最小差值，假设Δρmin>δd，此时，测量数据ρi，j可以看做测量噪声值而不参与障碍检测评估。δd代表激光雷扫描测距的标准差，在不同距离范围内，激光扫描测距的信息统计表，利用DAF可以有效去除脉冲干扰噪声和混合像素干扰，具体如表1 所示：

表1 不同距离标准差取值统计表

3 激光扫描下机器人运动目标跟踪技术研究

3.1 机器人坐标系与运动模型建立

在对移动目标进行跟踪时，常用坐标系统分为以下三种：第一种为机器人自身所在环境的全局坐标系[5]，描述为(XG，YG，ZG)，可以展示机器人在环境中位置变化情况；第二种为固定在机器人上的局部坐标系[6]，描述为(XR，YR，ZR)，第三种为通常情况下测距传感器反馈给机器人的数据信息构成的极坐标系，描述为(ρ，θ)，如图1 所示。

图1 机器人坐标示意图

针对坐标位置为[x，y，θ]T的机器人来说，其运动学模型可以描述为

(3)

式中，ω表示机器人中心点的角速度，v为线速度，则上述公式必须符合非完整性的约束条件，即

(4)

在实际跟踪过程中，机器人运动学参数受到动力约束[7]即

|v|≤vmax；|ω|≤ωmax

(5)

机器人在跟踪时，控制左右轮速度，即

(6)

在上述公式基础上，导出对应的离散化控制模型，即

(7)

3.2 目标检测视窗构建

当激光器与物体之间的差距大于三米时，数据点之间的距离明显增加，对获取目标数据信息产生不利影响。此时，只需要取三米之内的数据作为有效测量信息。并将存在不确定性因素信息剔除，可以减少计算机负担。因此，需要在机器人前方构建具有一定半径的滚动检测视窗[8]。

在机器人前方扩展一个半径为R的半圆检测窗口，α和β分别代表此窗口起点与终点的调度值，则该窗口的数学模型描述为W(R，α，β)，其中α=0°，β=180°，R=2m，R的取值和跟踪时机器人与运动目标理想的距离有关。

在激光扫描线与物体发生碰撞时，抵达物体到传感器位置的距离后dj返回，在窗口边缘之外的数据，如果di>dmax，则取di=dmax，即

(8)

式中，dmax属于视窗内运动目标实测距离最大值的阈值，dmax=R，dj表示构建视窗后第j个方向上的距离。

3.3 障碍空间聚类

通过二维笛卡尔矩形栅格[9]展示雷达扫描到的跟踪环境地图，利用二维数据组记载该环境中相对的栅格是否存在障碍物。如果栅格只存在空闲与占据两种情况，在已知每个栅格单元先验机率的基础上，采样时间点结合激光扫描到信息记载已知栅格的占据状态。

假设任意一个栅格存在障碍物且被扫描到，则该栅格的数据值设置为1。假设k-近临差值，Δρk为观测点(ρi，j，λi，j)中第k个邻近极角上点(ρi，j+k，λi，j+k)的距离，则

(9)

将测距信息根据下述原则划分成障碍区域，通过式(9)对比机器人在采样时间为i时两个邻近障碍物的距离Δρk，j与k分别从0和1开始，当k到达一定数值时，其附近区域中的最小差值△ρmin低于预测的阈值△ρset，此时j从0开始，到k个邻近角区域K中障碍全部当作同一类障碍。再从j+k开始，对障碍区域进行逐次聚类处理，在聚类后，任意一个障碍子集存在的特征表示为：

1)质心和质量属性

障碍子集中质量被称为子集On的栅格数量Mn，它取决于On的范围与栅格精准度。子集On的质心则取决于测量值和平均极角值[10]，即

(10)

(11)

Mn=k2-k1

(12)

根据机器人的位姿xrobot，yrobot，θrobot，将障碍集合On质心转化成全局坐标形式的质心坐标，其表示为

xn=xrobot+ρncos(λn+θrobot)

(13)

yn=yrobot+ρnsin(λn+θrobot)

(14)

2)障碍子集的运动参数

利用数据关联法则[11]，对函数获得的障碍信息进行评价，此时对障碍物运动速度评价表达式表示为

von=(On(i)-On(i-1))/Δt

(15)

式中，Δt表示采样周期，获取On的运动参数，对障碍物的运动状态进行评价，为后续跟踪提供依据。

3.4 运动目标检测

结合上述思想，对运动目标的起始与终止角度扫描的范围进行记载，并构建检测模型为(fk，sk，dmin)，f与s分别代表起始角与终止角，dmin为机器人和目标存在的最短距离。则该目标的位置坐标(xk，yk)的计算表达式为

(16)

获得机器人中点(xr，yr)与目标中点(xk，yk)的距离表达式

(17)

在对运动目标检测过程中，会存在误差，根据下述公式可对误差进行计算

σo=σd+σm

(18)

σm=(vr+vo)·(tsence+tprocess)

(19)

式中，σo为运动目标测量误差，σd表示激光扫描误差，vr代表机器人运动速度。在已知上述误差后对其进行补偿，从而提高跟踪精准度。

3.5 基于卡尔曼滤波的目标跟踪

卡尔曼滤波是对动态目标的状态做线性最小误差预测的方法。在本文中，激光扫描的运动目标在图像中，可以将其视为匀速运动，通过卡尔曼滤波器完成运动目标的参数预测。

假设一个随机动态系统的数学模型表示为

S(k+1)=H(k)S+n(k)

(20)

X(k)=F(k)S(k)+η(k)

(21)

式(20)属于状态方程，S(k)表示系统状态矢量，H(k)代表状态矩阵，n(k)表示噪声向量；式(21)为观测方程，F(k)是观测数据矩阵。并且n(k)与η(k)为均值是零的白噪声，满足高斯分布[12]

E[n(k)]=0，E[n(k)nT(i)]=Qk，i=k

(22)

E[η(k)]=0，E[η(k)ηT(i)]=Λk，i=k

(23)

定义机器人系统状态向量表示为X[x，y，vx，vy]T，x与y分别代表在x轴与y轴中坐标，vx和vy表示在两个坐标轴上的速度。在添加高斯干扰白噪声后获得运动目标的状态方程与观测方程分别为

X(k)=A(k-1)X(k-1)+ω(k)

(24)

Z(k)=H(k)X(k)+v(k)

(25)

式中，A(k-1)是在T周期基础上，从k+1时刻到k时刻的状态转移矩阵，其描述为

(26)

(27)

式中，状态噪声ω(k)与观测噪声v(k)均为零，即

ω(k)≈N(0，Q)

(28)

v(k)≈N(0，R)

(29)

4 仿真分析

为证明所提方法的合理性，设置仿真，并通过与感知代理和移动控制法则的分布式目标跟踪和无标定视觉伺服机器人跟踪控制的对比实验，验证方法的优越性。

4.1 仿真环境和参数设置

本次仿真在MATLAB平台上进行，操作系统为WINDOWSXP，系统运行内存为8GB，CPU为3.6GHz。

仿真参数设置如下：机器人运动速度为5m/s，运动目标速度是6m/s，扫描最远距离50m，测量间隔时间是0.3s，测量距离噪声0.2m，测量角度噪声π/180，跟踪范围是200m×200m。

4.2 结果分析

假设跟踪的机器人表示为A，运动目标为B，当B从t0时间点沿y轴方向进行直线运动，当B与A的距离高于理想距离时，A开始对B进行跟踪。采用不同方法对运动目标跟踪的轨迹结果如图2 所示。

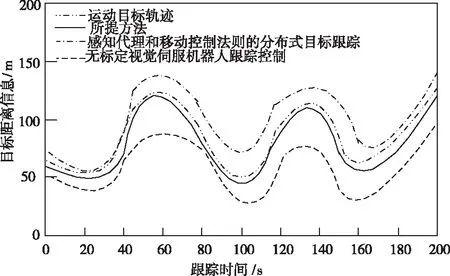
图2 不同方法跟踪轨迹对比图

从图中可以看出，本文算法的跟踪轨迹与运动目标轨迹更为接近，其它两种方法都会出现在某一时间点偏离目标轨迹的现象，这是由于所提方法在对运动目标进行跟踪时，将激光扫描技术中引入卡尔曼滤波的方法，降低了跟踪过程中其它噪声等因素的干扰，提升了所提方法的跟踪精度。

为进一步验证所提方法的可行性，实验分析了所提方法、感知代理和移动控制法则的分布式目标跟踪和无标定视觉伺服机器人跟踪控制方法对运动目标跟踪的效率，如图3 所示：

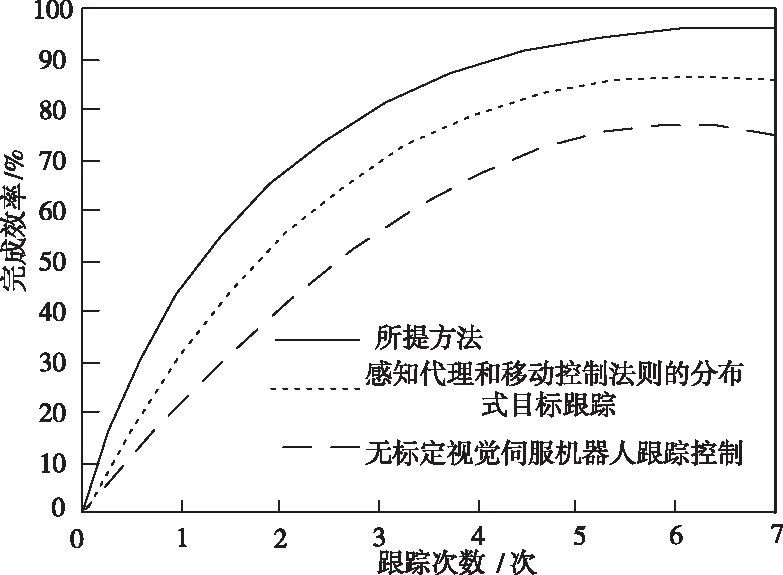
图3 不同方法跟踪效率对比图

分析图3 可以看出，采用三种方法对运动目标进行跟踪的效率不同。随着跟踪次数的改变，三种方法跟踪效率始终呈现上升趋势。其中，所提方法的跟踪效率最高约为97%，而其它两种方法的自动跟踪效率始终低于所提方法，验证了所提方法的可行性。

5 结论

针对传统机器人对运动目标进行跟踪时精度低的缺陷，本文在激光扫描基础上对机器人跟踪技术进行研究。通过对机器人坐标系与运动模型的建立，利用卡尔曼滤波器对运动目标进行跟踪，实现了机器人运动目标跟踪。与传统方法相比所提方法具有以下优势：

1)采用所提方法对目标运行轨迹的跟踪效果与实际运行效果较为接近，具有一定可信度；

2)采用所提方法对目标运行轨迹的跟踪效率最高约为97%，具有一定可行性。