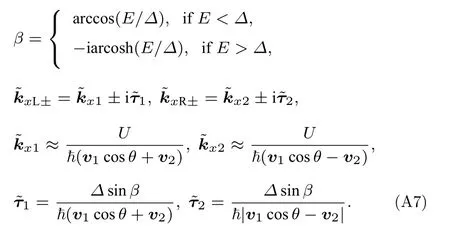第二类Weyl 半金属的金属-超导-金属结中的Andreev 反射*
2022-07-19陈书刚李学思韩宇
陈书刚 李学思 韩宇†
1) (辽宁大学物理学院,沈阳 110036)
2) (沈阳大学师范学院物理系,沈阳 110003)
理论上研究了第二类Weyl 半金属的金属-超导-金属(NSN)结在倾斜一定角度后体系的散射性质,计算结果显示倾斜角可以决定体系的散射机制,当倾斜角较小时,NSN 结中存在两种局域Andreev 反射和两种电子隧穿,包括径向Andreev 反射、镜面Andreev 反射、径向电子隧穿和镜面电子隧穿.随着倾斜角的增加,局域Andreev 反射逐渐被抑制,当倾斜角超过临界角后,NSN 结中的输运过程与正常金属的NSN 结相同,会同时发生电子正常反射、电子隧穿、局域Andreev 反射和交叉Andreev 反射.此外,体系的总电导不受化学势的影响,并且在倾斜角小于临界角时不受入射角的影响,而在倾斜角大于临界角时随入射角的增加而减小,而交叉Andreev 反射电导在某些条件下会随入射角的增加而增强.
1 引言
Weyl 半金属是一类新型的拓扑量子材料[1–6],它具有费米弧表面态、负磁阻效应等特点[7],在电子器件方面具有潜在的应用价值[8],受到人们的广泛关注.随着对Weyl 半金属研究的深入,第二类Weyl 半金属在理论上被预言并随后在 MoTe2[9–11],LaAlGe[12],WTe2[13–15],MoxW1−xTe2[16,17]等材料中得以实现.不同于第一类Weyl 半金属中点状的费米面[18],第二类Weyl 半金属具有过度倾斜的能带结构[19–21],因此具有有限大小的费米面,其Weyl点出现在能带中电子与空穴口袋边界处[22],费米面则同时穿过电子和空穴费米口袋[4].这种特殊的能带结构使得第二类Weyl 半金属具有很强的能带各向异性,这导致它除了具有与第一类Weyl半金属类似的性质,如拓扑保护表面费米弧、手征异常和大的非饱和磁阻[23–25]外,还具有额外的奇异量子特性[26],如反常量子霍尔效应[27]、手征反常朗道层面崩塌[28]等.
此外,倾斜的能带结构也带来了新的输运机制.在由正常金属(N)和超导体(S)组成的异质结界面会发生Andreev 反射现象[29],近年来被广泛地用于研究石墨烯类材料或新型拓扑材料的输运性质[30–39].在金属-超导-金属(NSN)结中[40–43],电子由一侧的金属入射,会发生4 种散射过程—电子正常反射、电子隧穿、局域Andreev 反射和交叉Andreev 反射[44–47].而第二类Weyl 半金属由于具有过度倾斜的能带结构,在它的NSN 结中电子正常反射和交叉Andreev 反射被完全抑制,取而代之的是两种局域Andreev 反射和两种电子隧穿[48].这种双Andreev 反射双隧穿的新型输运机制引起了人们的广泛关注.随后,很多第二类Weyl 半金属能带结构及其输运性质的相关工作相继被报道.如在第二类Weyl 半金属PN 结中,磁场下动量空间中的克莱因隧穿出现了新的量子振荡现象[49];在第二类Weyl 半金属的NS 结中,Andreev 反射具有极大的各向异性,可以用于检测第二类Weyl半金属的各向异性光谱[39]等.
本文在第二类Weyl 半金属NSN 结的基础上,将其倾斜一定的角度,通过散射矩阵方法计算体系的散射系数及电导以考察体系的输运性质.计算结果显示,倾斜角度决定着体系的散射机制,具体表现为当倾斜角较小时,NSN 结中存在两种局域Andreev 反射和两种电子隧穿,包括径向Andreev反射、镜面Andreev 反射、径向电子隧穿和镜面电子隧穿.随着倾斜角的增加,局域Andreev 反射逐渐被抑制,当倾斜角超过临界角后,NSN 结中的输运过程与正常金属的NSN 结相同,即电子正常反射、电子隧穿、局域Andreev 反射和交叉Andreev反射.此外,入射能、入射角、化学势以及超导体长度也会对体系的输运性质有不同程度的影响.最后,计算了微分电导,结果显示体系的总电导与化学势无关,并且在倾斜角小于临界角时不受入射角的影响,而在倾斜角大于临界角时随入射角的增加而减小,交叉Andreev 反射的电导则主要受偏压、化学势、倾斜角等因素的影响,在某些条件下可被增强.
接下来在第2 节给出了理论模型并通过散射矩阵方法计算了体系的散射系数;第3 节计算了体系的电导,并考察了体系的散射系数和电导随各参数的变化;第4 节给出结论.
2 模型与方法
本文研究的体系为第二类Weyl 半金属的NSN结,并将其倾斜一定的角度,如图1(a)所示.首先,第二类Weyl 半金属中其中一个Weyl 点K0处的低能有效哈密顿量可以写为[29,48]
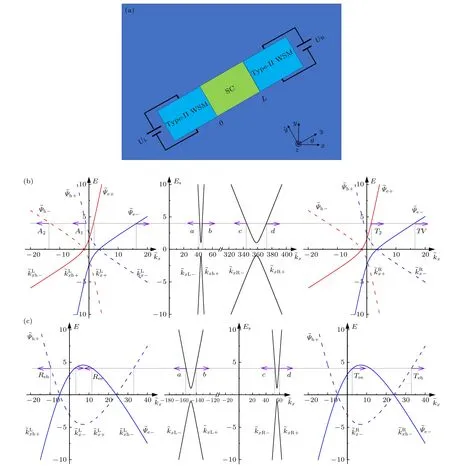
图1 (a)第二类Weyl 半金属的NSN 结倾斜θ 角度的示意图.在(b) θ <θc和(c) θ >θc两种情况下 ky和 kz 一定时NSN 结的能谱,其中红色(蓝色)表示导带(价带),实线(虚线)表示电子(空穴)Fig.1.(a) Schematic diagram of the NSN junction based on type-II WSM when changing the orientation angle θ.Energy spectra with finite ky and kz of the NSN junction for (b) θ <θcand (c) θ >θc,where the conduction (valence) bands are colored with red (blue),and the solid (dashed) lines denote electrons (holes).
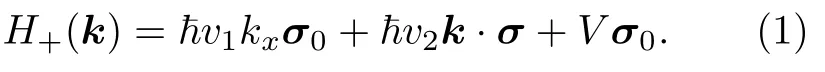
(1)式满足时间反演对称性而空间反演对称性破缺[50,51].其中k是一个可以保证低能模型有效的足够小的波矢量;σ(σx,σy,σz) 是泡利矩阵;σ0是单位矩阵;v2是费米速度;v1代表能带沿kx方向的倾斜程度;V是电化学势,可以通过门电压或者化学掺杂进行调节.相应地,另一个Weyl 点−K0的哈密顿量可以通过时间反演对称性写出:
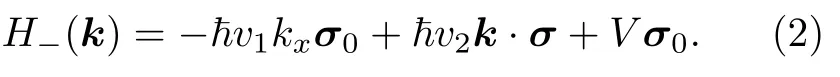
假设NSN 结的倾斜角度为θ,其取值范围为0◦<θ <90◦,为了方便计算,可以利用坐标变换
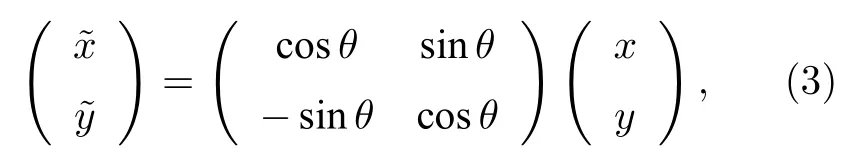
得到Weyl 点K0和−K0的有效哈密顿量:
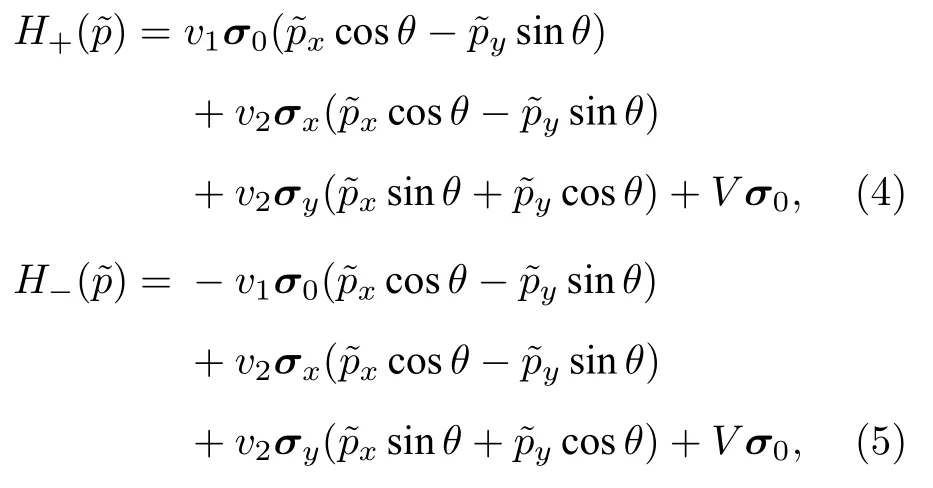
为了研究体系的输运性质,采用Bogoliubovde Gennes (BdG)方程描述电子和空穴的激发[52]:
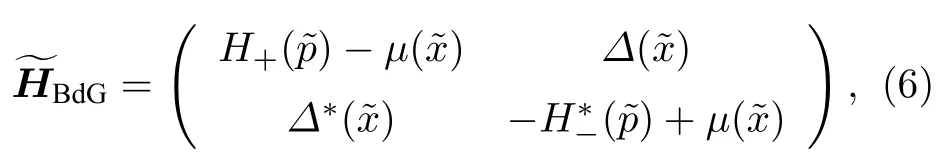
式中µ()为整个系统的化学势,∆() 为超导配对势,它们与电化学势V() 都属于阶跃函数:
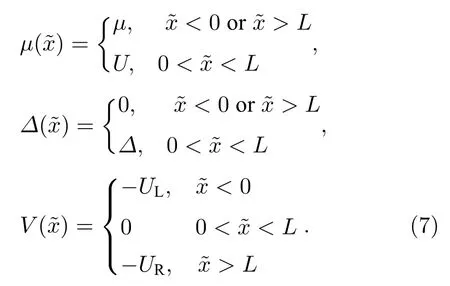
通过求解BdG 方程,可以得到超导体中准粒子的色散关系
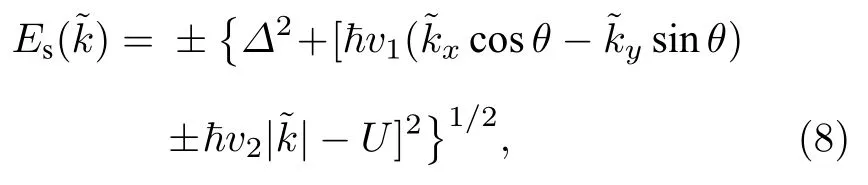
以及Weyl 半金属中电子和空穴的色散关系
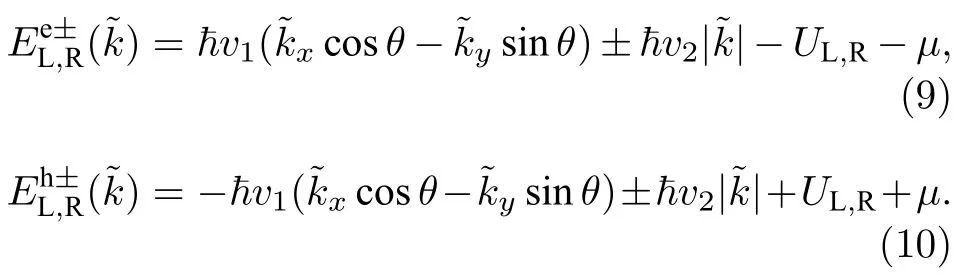
通过对超导结能谱的分析,可以发现NSN 结的倾斜角θ存在一个临界值θcarccos(v2/v1),当θ <θc时,在一定参数范围内体系仍然可以发生两种局域Andreev 反射和两种电子隧穿[29,48,53],如图1(b)所示.而当θ >θc时,在一定参数范围内体系会发生电子正常反射、局域Andreev 反射、交叉Andreev 反射和电子隧穿,如图1(c)所示.这两种散射过程只针对于第二类Weyl 半金属,而普通金属由于没有过度倾斜的能带结构,v1cosθ始终小于v2,因此无论倾斜角θ如何变化,其NSN 结中的散射过程始终保持不变.下面分别对这两种散射过程进行分析,由于体系是关于轴旋转不变的,接下来的讨论中,设置kz0.在这种情况下,入射角的范围为θ−αc≤α≤min(π/2,θ+αc),其中假设电子以入射能E,入射角α从左侧Weyl 半金属的价带通道Ee−入射,则超导结各区域的波函数可以写为
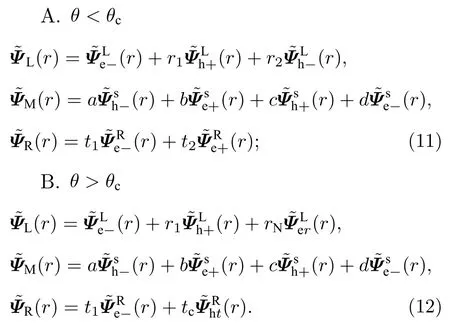
这些系数可以由两个界面处的边界条件

其中τz是泡利矩阵的z分量.
θ <θc时,径向和镜面Andreev 反射的系数A1和A2,以及径向和镜面电子隧穿的系数T1和T2分别为
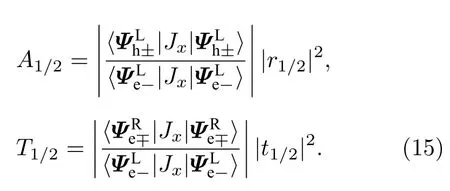
θ >θc时,局域Andreev 反射和电子正常反射的系数Reh和Ree,以及电子隧穿和交叉Andreev反射的系数Tee和Teh分别为
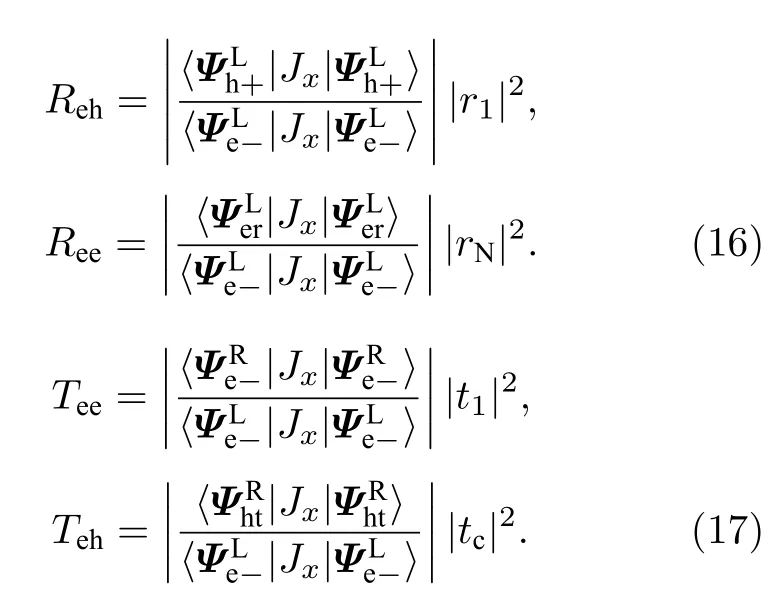
由于电流守恒,这些系数满足A1+A2+T1+T21,Reh+Ree+Tee+Teh1 的关系.
3 结果和讨论
本节考察体系的散射系数和电导随入射能、入射角及超导体长度等参数的变化,在接下来的计算中,取Δ=1 作为能量单元,其他参数都可用Δ表示,除非特殊说明,否则以下几个参数取值均为v21,kz0,∆1,U100,UL0,UR0.
首先考察的是θ <θc时,双Andreev 反射和双电子隧穿的系数随倾斜角θ的变化,如图2 所示,其中图2(a)和图2(b)的入射能分别取为E0 和E0.6.由图2(a)可以看出,当倾斜角0◦<θ <5◦时,径向Andreev 反射系数A1可以达到1,而其他的散射则被完全抑制.随着倾斜角θ的进一步增大,A1逐渐减小,镜面Andreev 反射系数A2和镜面电子隧穿系数T2先增大后减小,而径向电子隧穿系数T1则单调递增.当倾斜角等于临界角(θ ≈25◦)时,径向电子隧穿系数T1可以达到1,而其他三种散射系数则减小到0.对于入射能E0.6 的情况(图2(b)),可以看出当倾斜角θ较小时,镜面Andreev 反射的系数A2随θ的增加而先增大后减小,在倾斜角θ3◦时A2可达到1,径向Andreev反射的系数A1的变化趋势与A2正相反,而两种电子隧穿则几乎被完全抑制.随着倾斜角θ的增加,两种Andreev 反射的系数都呈下降趋势,镜面电子隧穿的系数T2先增大后减小,而径向电子隧穿系数T1单调增大,最终当倾斜角等于临界角时达到1.比较图2(a)和图2(b)可以发现,倾斜角对体系的散射性质具有较大影响,当倾斜角较小时,Andreev 反射占主导;随着倾斜角的增加,Andreev反射逐渐被抑制,电子隧穿逐渐占据主导地位;当倾斜角等于临界角时,体系只发生径向电子隧穿,其他散射过程被完全抑制.
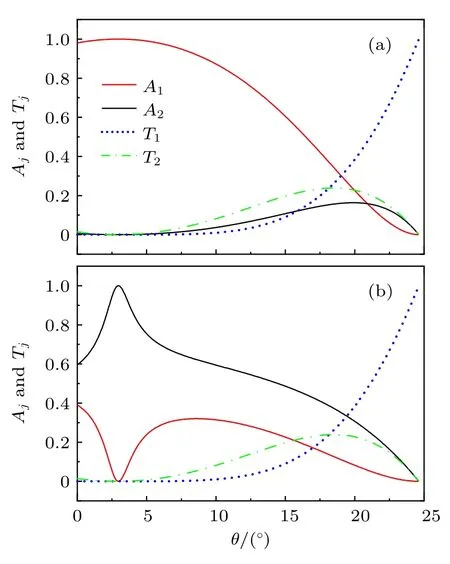
图2 θ <θc时,在入射能分别为(a) E0和(b)E 0.6时Andreev 反射和电子隧穿的系数随倾斜角θ 的变化.相关参数 为v1=1.1,v2=1,µ=0.5,UL=0,UR=0,α=30°,U=100,∆1,L=10ξFig.2.Andreev reflection and electron transmission coefficients as functions of orientation angle θ for (a) E0 and(b) E0.6 when θ <θc.Parameters:v1=1.1,v2=1,µ=0.5,UL=0,UR=0,α=30°,U=100,∆1,L=10ξ.
图2(b)中,当倾斜角θ3◦时,镜面Andreev反射系数A2可以达到1,因此,为了更好地观察Andreev 反射系数的变化,选取θ3◦研究两种Andreev 反射系数随入射能E的变化,结果如图3所示.其中图3(a),图3(c)和图3(b),图3(d)分别为选取不同化学势µ和能带倾斜系数v1时两种Andreev 反射系数的变化.图3(a)和图3(c)选取v11.1,可以看出当入射能E <∆时,体系只发生一种Andreev 反射,另一种Andreev 反射和电子隧穿被完全抑制.而当E >∆时,体系仍然只发生一种Andreev 反射,同时也发生电子隧穿,并且随着入射能E的增大,Andreev 反射系数伴随着振荡衰减.此外还可以看出,体系发生Andreev 反射的类型取决于入射能E与化学势µ之间的关系,当E <µ时,只发生径向Andreev 反射;当E >µ时,只发生镜面Andreev 反射;Eµ是两种Andreev反射互相转换的临界点.图3(b)和图3(d)选取µ0.5,可以看出除了v11.1的情况以外,当v1取其他数值时两种Andreev 反射共存,其中当入射能E <∆时,体系只存在Andreev 反射,电子隧穿被完全抑制,并且径向Andreev 反射系数A1随着入射能E的增加而减小,随着v1的增加而增大,而镜面Andreev 反射系数A2的变化趋势与A1正相反.当E >∆时,体系同时发生Andreev 反射和电子隧穿,两种Andreev 反射系数都随着入射能的增加而呈振荡衰减,并且A1和A2随着v1的增加分别增大和减小.
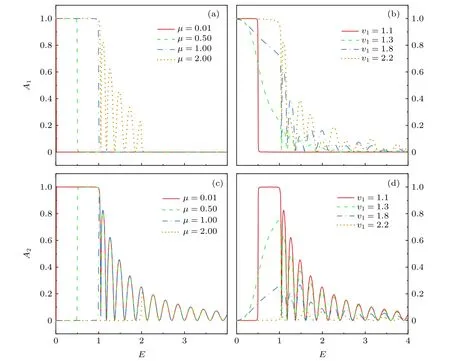
图3 θ <θc时,Andreev 反射和电子隧穿的系数随入射能E 的变化 (a),(c) v1 1.1;(b),(d) µ0.5.相关参数取值为θ 3◦,α30◦,v2 1,UL 0,UR 0,U 100,∆1,L10ξFig.3.Andreev reflections and electron transmission coefficients as a function of the incident energy E when θ <θc:(a),(c)v1 1.1;(b),(d) µ0.5.Parameters: θ3◦,α30◦,v2 1,UL 0,UR 0,U 100,∆1,L10ξ.
接下来考察θ <θc时,超导体长度L对体系输运性质的影响,结果如图4 所示.图4(a)和图4(b)分别表示入射能E0和E0.6 两种情况,其中倾斜角仍然与图3 一致,取为θ3◦.从图4 (a)可以看出,当入射能E0 时体系只发生径向Andreev反射(A1)和径向电子隧穿(T1),镜面Andreev反射(A2)和镜面电子隧穿(T2)被完全抑制,并且随着超导体长度L的增加,T1由1 逐渐减小,A1则由0 逐渐增加.当L3ξ时,T1减小到0,而A1增大到1,此后散射系数不再随超导体长度L的增加而变化.从图4(b)可以看出,当入射能E0.6时,体系只发生镜面Andreev 反射(A2)和径向电子隧穿(T1),径向Andreev反射(A1)和镜面电子隧穿(T2)被完全抑制,并且随着超导体长度L的增加,T1由1 逐渐减小,A2则由0 逐渐增加,最终在L3ξ时,A2和T1分别稳定在1 和0.
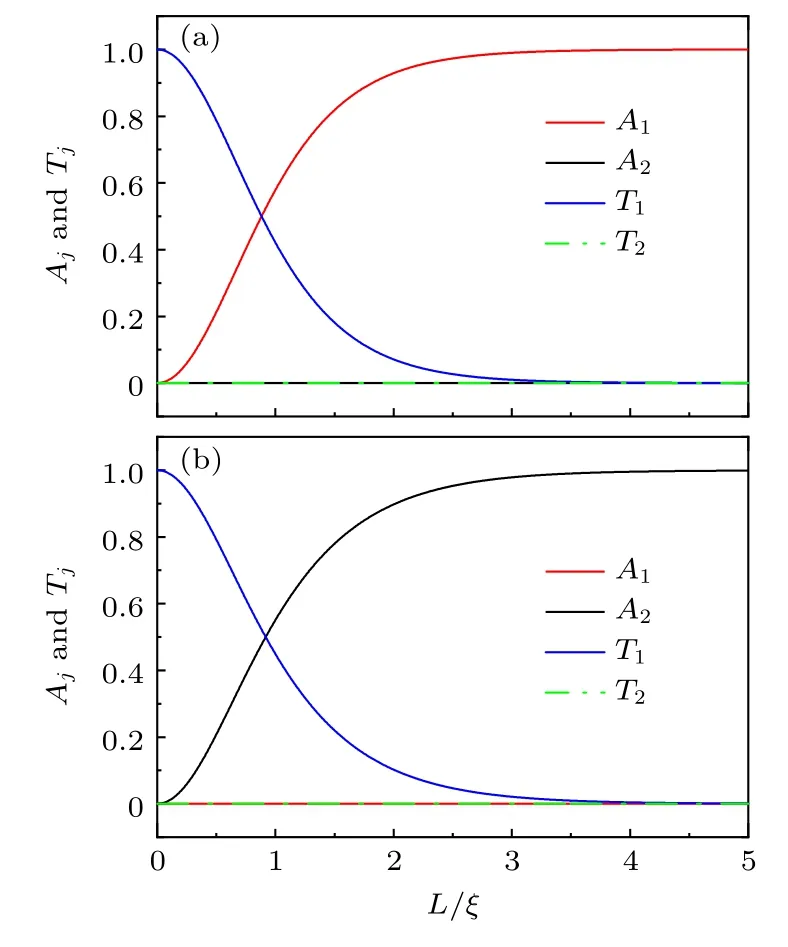
图4 θ <θc 时,Andreev 反射和电子隧穿的系数随超导体长度L 的变化 (a) E0;(b) E0.6.相关参数:v1 1.1,v2 1,µ0.5,UL 0,UR 0,θ 3◦,α30◦,U 100,∆1Fig.4.Andreev reflections and electron transmissions coefficients as a function of the SC region length L with incident energy (a) E0 and (b) E0.6 when θ <θc.Parameters:v1 1.1,v2 1,µ0.5,UL 0,UR 0,θ 3◦,α30◦,U 100,∆1.
接下来研究倾斜角θ >θc的情况.在这种情况下,体系会出现与普通金属的NSN 结类似的电子正常反射(Ree)、电子隧穿(Tee)以及局域Andreev反射(Reh)和交叉的Andreev 反射(Teh).首先考察这4 种散射系数随倾斜角θ的变化,结果如图5 所示.可以看出,这4 种散射系数随着θ的增加而呈振荡型的变化,当θ较小时,体系只存在电子正常反射(Ree)、电子隧穿(Tee)和交叉Andreev反射(Teh),其中电子隧穿的系数Tee随着倾斜角θ的增加而减小,电子正常反射系数Ree随θ的增加而增大,局域Andreev 反射(Reh)只在θ较大时出现,其系数Reh随着θ的增加而逐渐增大,交叉Andreev 反射的系数Teh随着θ的增加而先增大后减小,其中当倾斜角θ47.97◦时,交叉Andreev反射系数Teh达到最大值,接近0.4,如图5 中紫色圆圈所标记.选取这个最大值点,计算散射系数随入射能的变化情况,如图5 中插图所示.可以看出,随着入射能的增加,电子正常反射系数Ree单调递增,电子隧穿系数Tee和交叉Andreev 反射系数Teh先增大后减小,其中Teh的最大值可达到0.43 左右,而局域Andreev 反射则在整个入射能的范围内被完全抑制.上述现象说明,通过调整倾斜角可以在一定程度上增强交叉Andreev 反射,当倾斜角较大时,会对体系的输运性能起到消极影响.
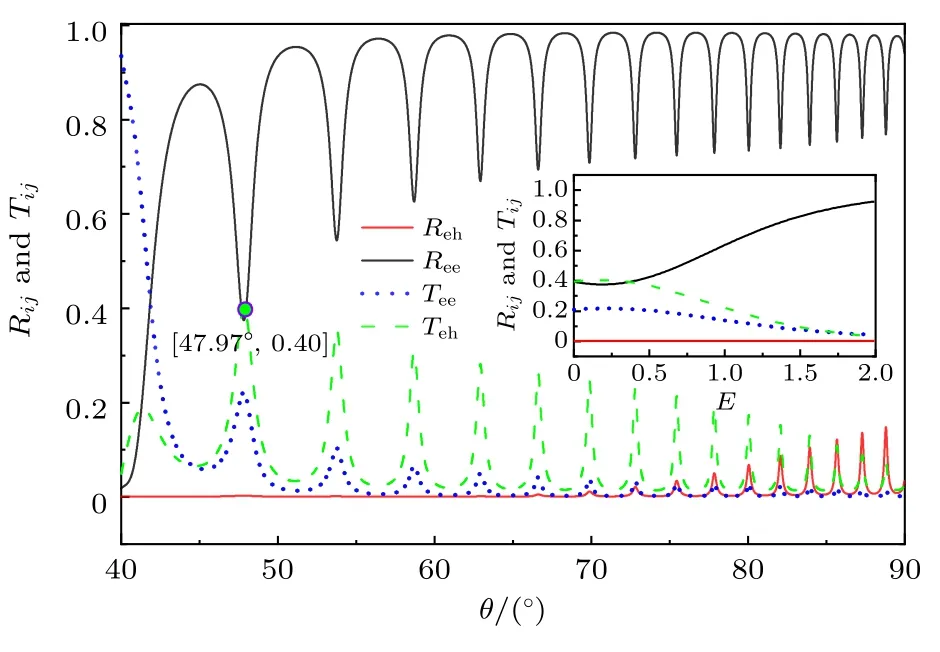
图5 θ >θc 时,Andreev 反射和电子隧穿的系数随倾斜角θ 的变化.插图为散射系数随入射能E 的变化.相关参数:E 0,v1 1.3,v2 1,µ0,UL 0,UR 0,α85◦,U 100,∆1,LξFig.5.Andreev reflections (Reeand Reh) and electron transmissions coefficients (Teeand Teh) as a function of orientation angle θ when θ >θc.The inset shows the scattering coefficients with the increment of the incident energy E. Parameters:E 0,v1 1.3,v2 1,µ0,UL 0,UR 0,α85◦,U 100,∆1,Lξ.
根据上述散射系数的结果,进一步计算体系的微分电导.由Blonder-Tinkham-Klapwijk (BTK)公式可得电导表达式为[29,54]

最后,考察体系的总电导G和交叉Andreev反射的电导GCAR随倾斜角θ和偏压eV的变化情况,如图6 所示.为了方便,取对电导进行规范.图6(a)为µ0.5,L10ξ,入射角α取不同值时,体系的零偏压电导G随倾斜角θ的变化情况,此时倾斜角的临界角为θc30◦.可以看出,当θ <θc时,总电导G随着倾斜角θ的增加而减小,当θ >θc时,总电导G随着倾斜角θ的增加而先减小后增大,最后稳定在G2.而入射角α的变化则主要在θ >θc时起作用,具体表现为总电导G随入射角α的增大而减小.当固定入射角α30◦,化学势µ取不同值时,总电导G不随化学势变化.图6(b)是入射角α取不同值时交叉Andreev 反射的电导GCAR随偏转角θ的变化情况,可以看出,入射角取不同值时,相应的电导都会在倾斜角θ取某些值时达到最大值,而后随着θ的继续增大而逐渐减小,最终在θ接近 90◦时减小到0.为了获得更大的交叉Andreev反射的电导,选取入射角α70◦时交叉Andreev反射电导GCAR的最大值点θ59◦,GCAR/GN0.24 (如图6(b)中紫色圆圈标记)画出交叉Andreev 反射的电导GCAR随偏压eV的变化情况.图6(c)和图6(d)分别取超导体长度Lξ和L10ξ.当Lξ时,从图6(c)可以看出,随着偏压eV的增加,交叉Andreev 反射的电导GCAR先增大后减小.在偏压较小时获得最大值,并且当偏压eV <0.5∆时GCAR随着化学势µ的增大而减小,当µ0.01 ,eV接近0 时,GCAR取得最大值0.29;而当偏压较大时化学势的改变对电导不会造成明显影响.当L10ξ时,从图6(d)可以看出,GCAR随偏压的增加而呈振荡变化,当eV1.7∆时取得最大值,可达到 0.4.此外还可以看出,当偏压eV <∆时GCAR随着化学势µ的增大而增大,而在eV >∆以后GCAR不再受到化学势的影响.
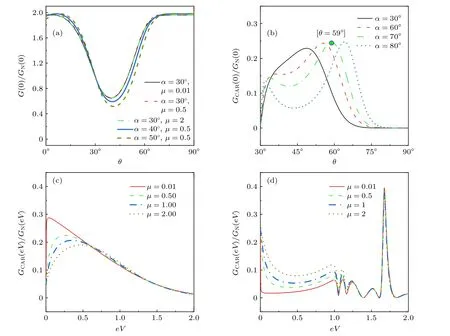
图6 总电导G 和交叉Andreev 反射电导 GCAR随(a),(b)倾斜角θ 和(c),(d)偏压 eV的变化.相应参数:(a),(b) µ0.5,L10ξ;(c)θ 59◦,α70◦,Lξ;(d)θ 59◦,α70◦,L10ξ.其他参数:v1 2/ v2 1,UL 0,UR 0,U 100,∆1, 10Fig.6. Conductance G and its CAR component GCARdependence of (a),(b) orientation angle θ and (c),(d) bias votage eV.P√arameters:(a),(b) µ0.5,L10ξ;(c)θ 59◦,α70◦,Lξ;(d)θ 59◦,α70◦,L10ξ.Other parameters:v1 2/v2 1,UL 0,UR 0,U 100,∆1, 10.
4 结论
本文研究了第二类Weyl 半金属的NSN 结在倾斜一定角度后体系的散射性质.计算结果表明,倾斜角度可以决定体系的散射机制,当倾斜角较小时,NSN 结中存在两种局域Andreev 反射和两种电子隧穿,包括径向Andreev 反射、镜面Andreev反射、径向电子隧穿和镜面电子隧穿.随着倾斜角的增加,局域Andreev 反射逐渐被抑制,当倾斜角超过临界角后,NSN 结中的输运过程与正常金属的NSN 结相同,即电子正常反射、电子隧穿、局域Andreev 反射和交叉Andreev 反 射. 此 外,入 射能、入射角、化学势以及超导体长度也会对体系的输运性质有不同程度的影响.最后计算了微分电导,结果显示体系的总电导与化学势无关,并且在倾斜角小于临界角时不受入射角的影响,而在倾斜角大于临界角时随入射角的增加而减小,交叉Andreev 反射的电导则主要受偏压、化学势、倾斜角等因素的影响,在某些条件下可被增强.由于本文中研究的参数较多,为了使读者更直观地获得本文的研究结论,我们汇总了各参数对散射系数的影响,如表1 所列.

表1 各参数对散射系数的影响Table 1. Influence of various parameters on scattering coefficient.
附录A第二类Weyl半金属的NSN 结在倾斜0◦时的本征矢量


当θ >θc时,左侧Weyl 半金属中的电子反射和右侧Weyl 半金属中的空穴反射分别可以写为
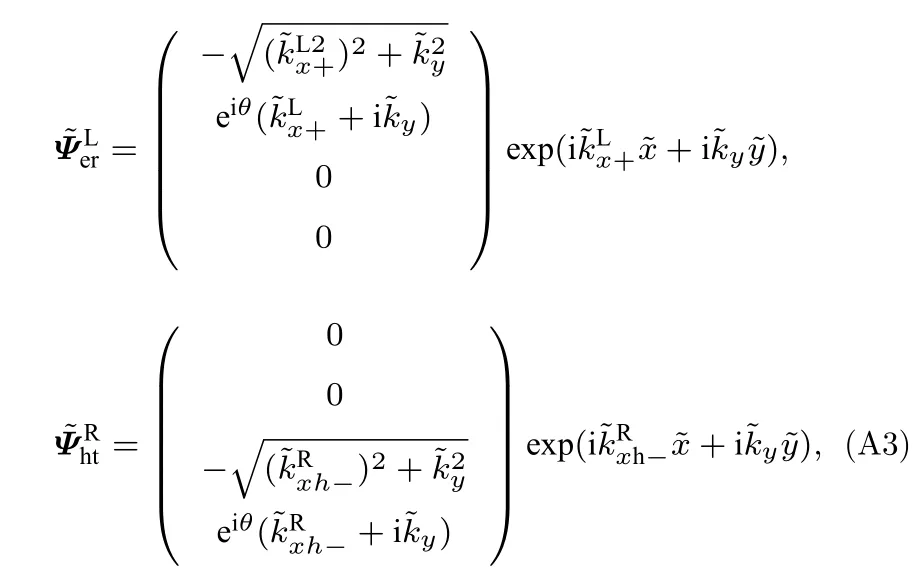
其中电子和空穴在方向的波矢量可以写为
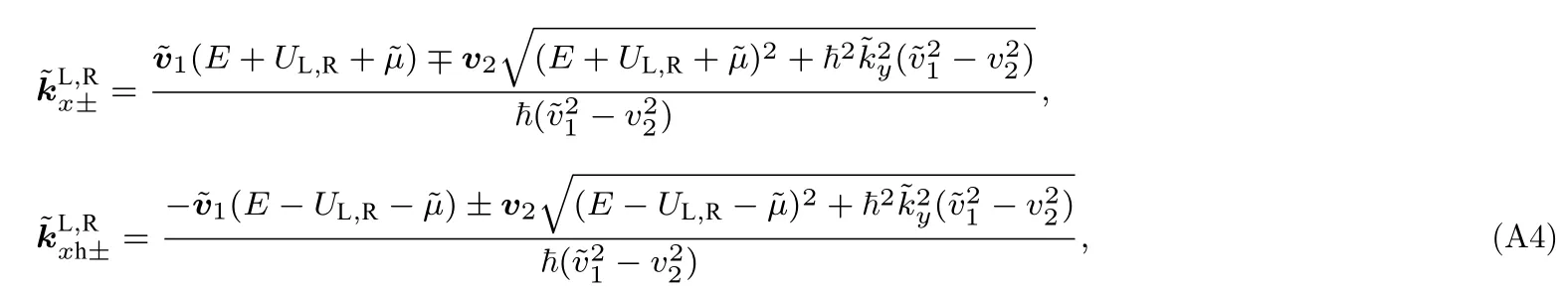
其中
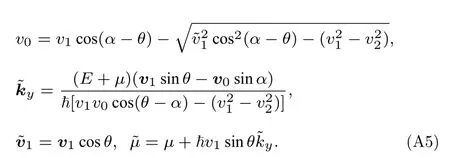
中间超导区域的散射模式可以写为

其中