低维材料中的电荷密度波*

樊金泽 方展伯 罗超杰 张汇†

1) (合肥微尺度物质科学国家研究中心,中国科学技术大学,合肥 230026)

2) (中国科学技术大学物理学院,合肥 230026)

电荷密度波(charge density wave,CDW)是低维体系中存在的一种重要的物理现象,对CDW 的研究有助于人们对低维系统中内禀电声子耦合和关联等相互作用有更深层次的认识,同时通过对材料中CDW 的精准调控可以有效控制低维材料中磁性、超导等物理性质.CDW 的研究最早起源于一维和准一维材料,本文首先简要介绍了CDW 的一些基本性质和一维体系中CDW 的一些研究.而近些年的研究发现CDW 在很多二维材料中普遍存在.本文将着重介绍二维材料中CDW 的最新研究进展.通过介绍二维材料中CDW 的基本物性和产生机理,讨论CDW 与Mott 相、超导序和其他序(自旋密度波、配对密度波)之间的相互作用;探讨CDW中存在的多电子集体激发和手性性质;介绍掺杂、高压和激光脉冲等手段对CDW 的调控;最后展望相关领域中可能的研究方向.

1 引言

电荷密度波(charge density wave,CDW)的理论最早被Frohlich 和Peierls 在1954 和1955 年相继提出[1],到现在已经是凝聚态物理中一种普遍的电子集体现象,并引发了人们对低维系统的广泛研究.在一维模型中,CDW 具有最简单的形式,可以通过Peierls 理论来直观地理解.对于图1(a)所示的一维均匀原子链,当每个原子提供一个电子时,能带呈半满填充,体系为金属性.Peierls 指出当考虑电子-声子相互作用时,这种一维原子链在低温下会不稳定,并发生晶格畸变.畸变时相邻两个原子之间会相互靠近,晶格的周期变为原来两倍,如图1(b)所示.与此同时在π/(2a)处,即新的布里渊区边界打开一个带隙,能带结构如图1(c)所示[2].体系由金属态转变为绝缘态,这种结构和电子态的变化称作Peierls 相变[3].能带为任意金属填充的一维原子链一般都会发生Peierls 相变,CDW 的波长λ与费米波矢kF间存在关系λπ/kF.畸变后电子体系的总能量的降低一般都大于晶格相互作用能的增大,这使得体系趋于稳定.同时晶格畸变导致了体系原有的平移对称性打破,体系中的电荷密度呈周期性分布,并构成CDW,可用方程ρ(x)ρ0+ρ1sin(2kFx+φ) 进行描述.

Peierls 相变背后的机理主要是费米面的嵌套所导致的Kohn 异常.在一维体系中,位于kF和–kF的两处费米面通过2kF的波矢相联系,即一个费米面可以经过一个特定的平移变换后与另一个费米面完全重合,这种现象被称为费米面嵌套.存在嵌套的费米面往往是不稳定的,其中的电子可被波矢为2kF的声子激发,导致该处的声子被重整化到更低频率上,促使系统发生声子软化,如图1(e)所示[4],这种现象被称为Kohn 异常[5].当温度达到CDW相变温度(TCDW)时,2kF处的声子频率会减小到零,此时晶格的振动恢复力消失,体系的平衡被打破,无需提供能量即发生稳定的畸变.费米面的嵌套一般通过Lindhard 电子响应函数来体现:

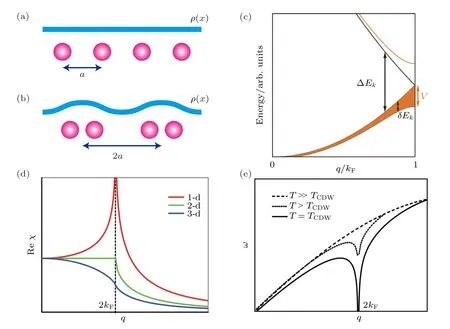
图1 一维Peierls 相变的基本原理 (a) 均匀排列的一维原子链示意图;(b) Peierls 相变后的原子链示意图;(c) 发生Peierls 相变前后的能带结构,能带在kF 处打开带隙[2];(d) 一维、二维和三维自由电子气的Lindhard 响应函数实部[4];(e) 2kF 处的声子软化过程[4]Fig.1.Fundamentals of Peierls transition:(a) Diagram of uniformly arranged one-dimensional (1D) atomic chain;(b) diagram of the 1D atomic chain after Peierls transition;(c) band structure of the 1D atomic chain before and after Peierls transition,with a gap opening at kF[2];(d) real part of Lindhard function for 1D,two-dimensional (2D) and three-dimensional (3D) free electron gas models[4];(e) process of phonon softening at 2kF[4].

其中f是费米分布函数,εk代表电子位于k点所具有的能量,ω为频率.Lindhard 响应函数描述了不同波矢处感应电荷密度随外加扰动势场的线性变化,实部反映了电子系统的稳定性,该部分会随着体系维度的变化而发生改变,一维到三维的响应函数实部如图1(d)所示.而响应函数的虚部则反映了费米面的拓扑性质[2].一维电子体系的费米面完全嵌套使得Lindhard 函数在2kF处发散.在真实材料体系中,往往通过Lindhard 响应函数的实部和虚部在CDW 的波矢处是否同时出现极大值,来判定CDW 是否由费米面嵌套引起.

此外自旋密度波(spin density wave,SDW)是一种与CDW 关系密切的有序态.SDW 的概念是Overhauser[6]在1962 年首先提出的,由于电子间的关联效应,电子气的顺磁排列会出现交换不稳定性,从而导致体系在基态自发形成自旋密度的有序排列.在一维模型中,Overhauser 理论是在原有CDW 的理论基础上额外考虑体系中的自旋自由度[7].即当体系上自旋和下自旋的密度函数中的周期调制相位差为0 时,体系中的自旋会相互抵消,从而不具备自旋调制而表现出CDW 的调制;但相位差为 π/2 时,体系自身产生了长程的自旋序,从而表现出SDW,此时空间中电荷密度却是均匀的;而当相位差在二者之间时,体系则呈现兼有电荷和自旋周期调制的混合态,此时CDW 与SDW 波矢之间的关系为QCDWQSDW.SDW 与CDW 的共同点在于都破坏了体系中的平移对称性,并能在费米面附近打开能隙来降低体系的总能量.但区别在于CDW产生时会伴随着畸变导致的晶格弹性能增加;而SDW 的产生并不会导致晶格畸变,同时与晶格弹性能提高所对应的是电子间相互作用能的增大.

一维CDW 材料的早期研究主要集中在有机导体TTF-TCNQ、过渡金属三硫化物MX3(M=Nb,Ta,X=S,Se)、蓝青铜K0.3MoO3、铂链化合物等[8].这些体系并不是理想的一维单原子链,但由于高度各向异性的电子结构和物理性质被称为准一维材料.理想准一维材料的费米面是两个完全嵌套的平面,这与一维单原子链具有相同的表现.而一般实际的材料总是存在较弱的链间耦合,只要费米面的弯曲程度足够小,体系还会存在一定程度的费米面嵌套,此时仍适用于Peierls 相变理论.很多实验也验证了准一维材料如TTF-TCNQ 具备良好的费米面嵌套[9],Kohn 异常[10],Lindhard 响应函数极大值[11],金属-绝缘体转变[12]等特征,与Peierls 理论能够保持一致[4].

而在近年热门的二维层状材料中,CDW 也广泛存在,并呈现出类似的特征.由于二维材料的电子结构更易受各种自由度的影响,且不像一维材料具有极强的电子关联效应,所以CDW 能与二维材料中丰富的物理效应相耦合.如CDW 可以和超导、Mott 绝缘体等共存并且相互作用,从而促使二维体系具有更丰富的物理性质,这为研究多电子集体激发和电子相互作用提供了新的视角.Dirac 半金属CeSbTe 中被发现存在CDW 与Kondo 效应的相互竞争,为研究Kondo 效应和非平凡能带拓扑提供了新的可能[13].此外,通过多种手段可以对二维材料中的CDW 进行更广泛的调控,尤其是近些年利用CDW 可以有效控制二维材料的磁性、超导等性质.本综述将着重介绍二维体系中的CDW以及相关的调控性质研究.

目前对CDW 的系统性综述主要集中在一维原子线[14]和准一维体系[1,15,16]中,距今已经有一段时间,而近些年二维材料的CDW 研究蓬勃发展,但现有的综述数量较少[17,18],还未完全覆盖CDW领域中的最新进展.本文将从一维体系开始,介绍CDW 的基本性质,如集体激发和调控技术等,然后重点介绍二维体系中CDW 的研究进展,包括产生机理,公度、激发和手性等性质,以及CDW 与超导、Mott 绝缘体、其他有序态如SDW、配对密度波(pair density wave,PDW)之间的相互作用,并广泛地涉及了现有的调控手段,为CDW 的性质提供较为完整的图像.在最后对CDW 领域的研究方向和潜在应用进行了展望.

2 CDW 在一维体系中的研究

由上述介绍可以看到,一维和准一维材料中的电子被强烈束缚,从而产生特殊的色散关系和费米面.而电荷、自旋和晶格振动等自由度之间的耦合增强,会导致在一维体系中出现CDW、Luttinger液体[19]、一维 Wigner 晶体[20]等现象.随着分子束外延(molecular beam epitaxy,MBE)技术和各种微观及能带表征技术的出现,基于表面体系的一维原子链/准一维原子链为一维性质的研究提供了重要平台.这类材料具有量子限域效应[21,22]、金属绝缘相的共存和涨落[23]、自旋电荷分离[24]、拓扑孤子激发[25]和一维拓扑相变[26]等性质.基于半导体表面自组装的原子链体系包括Si (111)-Au-5×2 重构[27]、Si (55×)上Au 原子链重构[28,29]、Si (111)-In-4×1 重构[30]等.以双排In 原子链组成的4×1重构为例.利用结构测量技术并结合理论计算[31,32]可以建立一个清晰的4×1 原子链模型,并可完美解释观察到的电子特性、光学响应特性等.这种材料在室温下具有3 个准一维的金属带[33],并分别具有不同的填充,其中一个能带刚好为半满,在低温下表现出Peierls 不稳定性.实验上韩国永熙大学的Yeom 团队[34]基于角分辨光电子能谱(angleresolved photoemission spectroscopy,ARPES)和扫描隧道显微镜(scanning tunneling microscope,STM)观察到该体系存在金属-绝缘体转变.当温度低于120 K 时重构转变为4×2 重构,继续冷却后转变为8×2 结构.而随后Tanikawa 等[35]通过微观的四探针技术证实小于130 K 时系统存在金属-绝缘体的转变.但关于低温相的原子结构以及相转变机理仍有争议.利用trimer 模型可以对实验中的8×2 结构进行解释[31],但这种模型无法解释绝缘相的存在.此后González 等[32,36]提出的六角模型可以完美解释实验中费米面上的带隙[35,37].由于链上的剪切形变需要的能量很低,因此实验上可以观察到整个体系会在四重简并的4×2 基态之间涨落[37].

对于这类原子链材料中CDW 的产生机理,ARPES 的测量表明金属-绝缘体转变与费米面钉扎的CDW 机制不同,可表现为有序和无序之间的转变[37].而在另一个常见的AuSi (557)原子链体系中,由于缺陷等因素的存在,其CDW 的机理也很复杂[14,29].而随后的研究还发现纳米线的尺寸等也会对CDW 的性质产生很大影响[38].而在相转变点附近还发现了很多一维CDW 的短条纹,这些条纹能在一些缺陷附近钉扎形成畴,如图2(a)所示,但这些畴中的重构类型以及电子态并不是完全对应的,这也使CDW 在结构和电子相变的驱动问题上出现了很多争议[33,39].传统的观点认为电声子耦合使声子软化,从而导致了结构发生变化并改变电子能带结构.但在实际的体系中,由于原子链不能处于绝对自由状态,受到缺陷、自身结构、重构以及衬底电荷转移和应力等的影响,其相变时的两相之间的能垒差异发生变化,从而极大程度地改变相变时的环境和相变条件.这也是促使相变与传统理论上产生差异可能的原因.而在后来发展的二维体系中,由于上述的环境变得更复杂,加上能带结构和电声子耦合也发生很大改变,使得这些体系的相变条件与原有的理论相比发生了极大程度的改变,并在不同实验中有较大的浮动,这也导致了包括相变激励等的争议,并促使了后续对CDW 低能激发态的探索以及CDW 调控的研究.

图2 (a) In-Si 原子链在Peierls 相变时的STM 图,插图是In-Si 原子链相变前后的重构[39];(b) In-Si 原子链中存在的手性拓扑孤子的STM 图[52];(c) 缺陷调控的In-Si 原子链金属相和绝缘相共存,插图为缺陷密度对4×1 相的面积分数的调控作用[58];(d) MTB结构的示意图[62];(e) 二维材料MoSe2 中MTB 的STM 图[63];(f) STS 测量的二维材料MoSe2 中MTB 和畴中心的dI/dV 谱[63]Fig.2.(a) STM image of Peierls transition in In-Si atomic chain.Inset:4×1 reconstruction before the Peierls transition and 8×2 reconstruction after the Peierls transition[39].(b) STM image of chiral topological solitons in In-Si atomic chain[52].(c) STM images of the coexistence of metallic phase and CDW phase in defect-rich In-Si atomic chain.Inset:manipulation of defect density on areal fraction of 4×1 phase[58].(d) Diagram of MTB structure[62].(e) STM image of MTB in 2D material MoSe2[63].(f) dI/dV spectrum of MTB and domain center in 2D material MoSe2 measured by STS[63].

此外对CDW 激发态的研究也是近年的一个重要研究方向.在一维体系中,CDW 的激发态主要有相位模式、振幅模式以及孤子激发[15].而孤子激发是该体系中研究最热门的方向.孤子在传统高分子材料中可充当载流子的作用[25,40],但因有效质量太小很难在实验中观察到.在准一维材料体系中,由于公度的CDW (commensurate charge density wave,CCDW)的排列与晶格间有固定相位,两个周期之间的作用会变得显著,也会导致孤子等非线性激发,使材料具有非线性和频率依赖的集体输运性质[15].TTF-TCNQ[41],NbSe3[42],TaS3[43],(Per)2M(mnt)2(M=Au,Pt,Co)[44]等材料都在低温下具有类似的非线性输运表现,在施加电场小于阈值电压时体系呈现欧姆特性,而当超过阈值电压时电导会随电场的增大出现非线性增加.材料的阈值电压依赖于温度,其大小与杂质的含量和样品尺寸等有关[45].此外NbSe3[46],TaS3[47]的电导都呈现出对频率的过阻尼响应,在较高频率下出现最大值,且该点对应的能量远小于单粒子带隙的跃迁,表明这种频率依赖性来自于集体激发.TTF-TCNQ 的输运现象则与其一维特性直接相关,施加电场后平行链方向电导非线性增大,而垂直链方向的电导则保持不变[41].而在一维的In 原子链中,中国科学技术大学的曾长淦教授团队[48]利用STM 观察到了孤子,并对孤子的生成、扩散等做了相应的研究.而Yeom 等[49−51]也对该体系中存在的孤子进行划分,并发展出具有可用于未来高性能计算的手性拓扑孤子.此后的研究也厘清了材料中不同孤子和各种缺陷间的关系,如图2(b)所示[52].

此外,金属-绝缘体转变的性质还可以通过外界因素进行调控.例如气体分子的吸附可以有效钉扎住一维体系里的CDW 相[53,54].而利用光照和半导体材料的能带弯曲可以实现电子注入,从而改变CDW 态在表面的分布[55].Yeom 等[56,57]利用掺杂Na 原子的In 原子链,发现除实现了材料中的电子注入,还可以引起周期性的晶格扰动,并产生局域沿链×1 方向的周期型调制.而曾长淦团队[58,59]也在随后的研究中发现,通过可控的缺陷密度并产生可控的应力场以及针尖施加的电场,都可对CDW态和金属态之间的比例进行调节,从而在一些简单体系中实现电子相分离相的基态,如图2(c)所示.而不同的缺陷类型也会导致不同的绝缘相的形貌和大小产生差异[60].

除了在基于半导体表面的金属原子链体系中开展的CDW 性质的研究,近些年在一些二维材料表面的一维缺陷结构中也发现了类似的CDW.在2H-MoSe2中,两个旋转60°畴的相交边界处会形成一维的线缺陷,被称为镜像孪晶界(mirror twin boundaries,MTB)[61],如图2(d)[62]和图2(e)[63]所示.香港大学的谢茂海团队[64]通过扫描隧道显微谱(scanning tunneling spectroscopy,STS)研 究发现在2H-MoSe2中,MTB 的电子结构呈现为体态带隙中的分散金属能带.如图2(f)所示,由于其态密度完全位于MoSe2的带隙内且不与畴内的电子态耦合,让电子限制在一维缺陷中,所以MTB 是理想的一维体系[63].而之后的STS 研究发现低温下MTB 中在费米能级处打开了带隙,并且沿MTB方向的态密度存在周期性调制,波长约为3 倍晶格常数,这说明MTB 中可能存在孤立的一维CDW[65].ARPES 研究则显示MTB 具有平行的费米面,符合完美嵌套的条件,并且相应的CDW 波矢与实空间测量一致[66].而近年的理论研究也指出材料中的固有极化使得MTB 中的金属带具有1/3 填充,容易受到Peierls 不稳定性的影响,并且可能出现CDW 与SDW 的组合态,允许携带分数电荷的孤子激发[67].但因目前的研究都是在较短的MTB 上进行的,无法排除有限长度下的一维量子限制效应,而谢茂海团队[62]也对不同衬底上不同长度的MTB 进行了研究,发现其中电荷密度调制在室温也可以观察到,这与CDW 的表现不符,有可能是一些量子限域效应和Friedel 振荡所导致.

3 CDW 在二维体系中的研究

一维体系中虽然表现出明显的CDW 特性,但由于材料制备和测试技术的限制,使得其在未来应用方面存在较大瓶颈.近些年发展的二维材料受材料自身的结构稳定性以及衬底等影响,会表现出与传统三维材料和一维材料截然不同的丰富物理性质,这也让二维材料成为近些年凝聚态和量子物理研究领域里最热门的研究方向.目前二维材料主要有:单质类单层蜂窝状结构材料、过渡金属二硫化物 (transition-metal dichalcogenides,TMD)材料、半导体表面的金属薄膜和金属原子链、界面异质结材料以及单层化合物薄膜材料等.而近些年叠堆魔角石墨烯、Kagome 超晶格等人工构造的新型准二维材料的出现,更极大程度拓展了二维材料的种类,为探索更多低维材料的物性奠定基础.

目前CDW 可广泛存在如TMD 材料,层状具有尖晶石结构、Kagome 晶格或Kondo 晶格的单晶材料,一些高温超导铜氧化合物以及部分金属薄膜材料等.常见二维材料的CDW 性质如图3 所示[68,69].与最简单的一维情况相比,二维体系中CDW 的成因更复杂,与此同时其性质也更加丰富.二维体系中的CDW 可以与超导共存并相互作用,还可以具有一定的三维性质和手性,在同一种材料中CDW 可以存在多种不同公度的结构形式.而且随着层厚的降低,层间范德瓦耳斯作用不断减弱,材料可从各向异性的三维结构过渡到准二维层状结构,再过渡到单层结构,其结构和电子态的性质也发生相应改变,为二维体系中的CDW 调控提供了更多可能.

图3 常见二维材料的CDW 性质,数据来源于文献[68,69].Fig.3.CDW properties of 2D material,data from Ref.[68,69].

3.1 二维体系中CDW 的起因

一维体系中的CDW 相变可以用Peierls 理论较好地解释,但在二维材料中,由于复杂的晶格和电子结构,CDW 的起源问题存在很大的争议.研究发现在一些具有费米面嵌套的二维和三维系统中(如部分铜氧化物材料[70]、单层VSe2[71,72]和CeTe3[73]等),由于材料的能带结构中拥有接近直线的平行费米面,如图4(a)所示,很容易存在费米面的完美嵌套,符合Peierls 理论.图4(b)给出了单层VSe2的三组嵌套波矢.但其他体系中的CDW 是否也来源于费米面嵌套,目前还存在较大争议.实验上在一些不存在费米面嵌套的材料中也观察到了CDW的存在;而在另一些存在嵌套的二维体系中,电荷序发生的相变与Peierls 相变的特征并不完全相符.尤其是2H-NbSe2在33.5 K 时会发生二阶CDW相变,并呈现出3×3 超晶格结构.ARPES 证实该体系费米面具有一定的嵌套特征[74,75],但输运性质表明该体系在33.5 K 以下并不是绝缘态,只是电阻略微上升,体系仍是良好导体[76].Lindhard 响应函数的计算结果也表明,费米面嵌套确实存在,但其导致的强峰与CDW 波矢位置不符;而在CDW波矢附近,响应函数的实部有较弱的峰值,虚部则没有出现,这与传统的Peierls 相变特征不符合.由于实部的峰值不足以激发CDW,这就排除了费米面嵌套作为直接因素的可能[77].Arguello 等[78]通过准粒子相干散射技术,发现2H-NbSe2中费米面嵌套不是准粒子散射的主要贡献,并且CDW 波矢处的散射信号在费米能级附近没有表现出色散特征,也说明了该CDW 与费米面嵌套无关.

为了更进一步理解2H-NbSe2等二维体系中的CDW 相变,Rice 和Scott[79]在1975 年提出了鞍点理论.该理论与费米面嵌套理论类似,具体可表现为:2H相材料的费米面在布里渊区内会两两相交,并在费米面附近产生6 个费米速度很小但态密度很高的鞍点.鞍点之间可以利用波矢相连接,这使得体系的声子软化,并合成3 对CDW,而畸变后的相则呈现金属态.在层状Kagome 材料AV3Sb5(A 为K,Rb 或Cs)中,布里渊区的边界M点附近存在高态密度的鞍点,如图4(d)所示[80].南京大学的闻海虎团队[81]发现CsV3Sb5中CDW形成时会明显抑制鞍点附近重空穴能带的光电导权重,同时鞍点附近态的带间跃迁增强并向高能量范围转移,这也证实了鞍点嵌套对驱动CDW 的不稳定性起到的重要作用.而中国人民大学的王善才团队[80]对RbV3Sb5的ARPES 研究发现,CDW 形成后,布里渊区边界处的能带向下移动并在M点打开能隙,这表明鞍点处的能带重整化对CDW 的形成有重要作用.

图4 二维体系中CDW 产生的几种机理图 (a) ARPES 测量的单层VSe2 费米面结构[71];(b) 单层VSe2 中的完美费米面嵌套[71];(c) 通过非弹性X 射线散射测量的不同温度下2H-NbSe2 中电声子耦合导致的声子软化[84];(d) ARPES 测量的RbV3Sb5 费米面结构,在鞍点处有高态密度[80];(e) 1T-TiSe2 中Jahn-Teller 畸变示意图[92];(f) 1T-TiSe2 中普通态和激子绝缘体的能带色散和光谱权重[94]Fig.4.Several mechanisms of CDW transitions:(a) Fermi surface map of monolayer VSe2 measured by ARPES[71];(b) perfect Fermi surface nesting of monolayer VSe2[71];(c) phonon softening in 2H-NbSe2 at different temperature induced by Electron-phonon coupling,measured by inelastic X-ray scattering[84];(d) Fermi surface map of RbV3Sb5 measured by ARPES with high density of state around saddle point[80];(e) diagram of Jahn-Teller distortions in 1T-TiSe2[92];(f) band dispersions and corresponding spectral weights of normal state and exciton insulator in 1T-TiSe2[94].

而在2H-NbSe2等材料中,尽管鞍点理论可以解释金属-绝缘体转变的缺失,但在其他性质上与实验还存在着一些出入.此后学界出现了一种更公认的观点:利用波矢依赖的强电子-声子耦合理论来解释如2H-NbSe2等TMD 材料中的CDW.电子-声子耦合与费米面嵌套等都来源于电子和晶格之间的相互作用,且二者都涉及电子从满态向空态之间的激发,但区别在于费米面的嵌套是典型的声子对电子的弹性散射,而电声子耦合是电子和声子间的非弹性散射过程,其选择的波矢不一定嵌套在费米面处[82].在2H-NbSe2体系中,ARPES 的研究发现CDW 相变对费米面附近的电子结构影响较小,而电声子耦合是准粒子自能改变的主要贡献,并展现出很强的各向异性[83].此后一些实验也观察到CDW 在费米面附近打开带隙,并由CDW波矢相连接.由于CDW 带隙小到不足以对输运性质产生影响,这也解释了金属-绝缘体相变的缺失[75].非弹性X 射线散射实验则证实了CDW 波矢处的声子能软化到零,并导致晶格畸变.但与Kohn 异常存在的色散尖峰不同,声子在CDW 波矢附近的区域会呈现过阻尼状态,如图4(c)所示,这更符合电声子耦合的理论计算[84].此后声子谱的光学支中也观察到了电声子耦合的存在,进一步的理论计算说明电声子耦合主要来源于电子在费米面处Nb原子的4d 衍生带之间的散射过程[85].STS 实验表明,不同于Peierls 相变中电子结构改变主要在费米能量附近,NbSe2进入CDW 态时电子结构会在–0.7 eV 的CDW 波矢处发生改变,而费米能级处的改变较弱,这也表明强电声子耦合才是NbSe2中CDW 形成的主要原因[86].之后对单层1H-NbSe2的STM 的研究发现,单层中Γ点和K点处的内口袋消失,但CDW 保持不变,这进一步排除了费米面嵌套的可能[87].

而在另一些体系中CDW 也可能来源于其他物理机制,如1T-TiSe2在200 K 下发生的CDW相变,并形成具有2×2×2 超结构的公度CDW[88],其背后的驱动机制比2H-NbSe2更为复杂.由于1TTiSe2的能带结构中不存在相互嵌套的费米面[89],这基本可以排除费米面嵌套的可能性.但对于电声子耦合[90]、Jahn-Teller 效应[91,92]、激子绝缘体[93,94]等几种驱动机制,尽管有许多理论和实验研究,目前仍旧存在许多争议.Jahn-Teller 效应和激子绝缘体的机理分别如图4(e)和图4(f)所示.

3.2 二维材料里的公度CDW 与非公度CDW

公度是一维体系和二维体系中的CDW 所共有的性质.如果CDW 的波长λ与原晶格常数a之间的比值为有理数时,称为公度的CDW (commensurate charge density wave,CCDW),此时λ与a之间存在最小公倍数.CCDW 态在平衡位置之间的转变需要跨越较高势垒,因此表现出明显的晶格钉扎;而当λ/a是无理数时,称为非公度CDW (incommensurate charge density wave,ICCDW),每个原子会轻微离开原有位置,λ与a之间的最小公倍数则会趋于无限大,此时CDW 和晶格之间的相互作用与相对位置之间不存在对应关系,晶格无法钉扎CDW,体系则更容易被直流电场推动.

在一维材料中,如K0.3MoO3,NbSe3等材料在低温下具有约4 倍晶格常数的公度CDW,但当温度高于转变温度后,CDW 的波矢会增大并变成非公度的CDW[1].而TTF-TCNQ 的链间CDW 会随着温度的降低,从2 倍晶格常数的公度CDW 转变为非公度CDW,再到4 倍晶格常数的公度CDW[16].在二维材料中,CDW 则呈现出更复杂的结构形式,如1T-TaS2在高温下呈明显的金属六方相,而当温度低于550 K 时则形成非公度的CDW,此时体系仍具有良好的金属性;当温度低于200 K 时,强的电声子耦合会使体系进入CCDW 态,其中12 个Ta 原子会向中心原子聚拢,形成周期为的超结构,这种结构被称为David 星[95],David 星的形成会伴随着Ta 原子的5d 价带分裂和费米能级处子带的变窄[96].此外在CCDW 与金属相之间还存在着一种一维体系中不存在的近公度CDW相(nearly commensurate charge density wave,NCCDW),这种CDW 是由局域的公度畴和非公度畴壁网络组成,其中六边形的公度区域为互不相连的六角排列,之间的空隙则为三角形,并展现出类似于Kagome 晶格的平面结构,如图5(a)所示[97].近些年的研究还发现,这种二维CDW 结构上的差异对材料自身的物理性质有很大的影响,例如在1T-NbSe2,1T-NbS2等体系的CCDW 态中,每个David 星的形成会在其中心产生一个局域磁矩,如图5(b)所示[98−100].美国德州大学奥斯汀分校的施至刚团队[99,100]在1T-NbSe2/2H-NbSe2垂直异质结中发现了Kondo 共振和Yu-Shiba-Rusinov束缚态,这也表明1T-NbSe2中的局域磁矩与2HNbSe2中的电子或库珀对之间存在交换作用.并且Kondo 峰的振幅具有与David 星自旋密度相关的空间调制.这不仅为1T-NbSe2中电子关联驱动的大局域磁矩提供了明确证据,同时还为未来新型拓扑超导材料的开发提供了方向[99].而在2H-NbS2中,退火可以引入少量的1T-NbS2原子层.这种自发形成的异质结也会导致体系的面外电导率出现明显的Kondo 效应,并表现出对磁场的高度各向异性响应[100].

图5 (a) 1T-TaS2 中的David 星、CCDW、NCCDW 示意图[97];(b) 2H-NbS2 中的1T 层示意图,每个David 星中心都有一个未配对的局域磁矩[100]Fig.5.(a) Diagrams of the Star of David pattern,CCDW,and NCCDW in 1T-TaS2[97];(b) Diagram of the 1T layer in 2H-NbS2,each Star of David contains an unpaired magnetic moment localized in the center[100].

3.3 二维材料中的CDW 调控

在一维体系中,通过温度、应力和局域电场等能够对材料中的CDW 产生一定程度调制,而在二维材料里,这些调控手段同样可以实现从CCDW向NCCDW 或ICCDW 的转变;此外由于维度的增加,对二维体系CDW 的调控方法较一维体系增加很多.研究发现,通过施加垂直电场或光学激发等可以在1T-TaS2中掺入空穴,并能稳定晶格促使体系从CCDW 转变为NCCDW 或某种亚稳态.复旦大学的张远波团队[101]和Yeom 团队[102]发现利用STM 的针尖对样品施加正电脉冲可以有效抑制低温下绝缘相的出现.施加脉冲后体系表面会形成局域的CCDW 畴和不规则的ICCDW 畴壁,呈现出金属镶嵌相,如图6(a)所示.新产生的CCDW区域仍为David 星构型,但已具有不同的层间堆叠顺序.而当温度升高后体系的非公度畴发生熔化,表面便产生了不可逆的绝缘态转变,这也说明体系诱导出的是一种亚稳相.皮秒激光脉冲可使CCDW相的1T-TaS2发生可逆的金属-绝缘体转变,并诱导出一种稳定的金属隐藏态;而当升温或者施加电流及激光脉冲后体系会恢复到原有的CCDW 态[103],过程如图6(b)所示[104].之后的STM 研究发现这种金属隐藏态的稳定性与长程拓扑电荷序有关[105].而通过面内脉冲电流也可实现快速的金属-绝缘体转变.转变时临界载流子密度与CCDW-NCCDW相变的临界载流子密度相当,这说明载流子驱动了绝缘带隙的坍塌,促使体系转变为NCCDW[106].之后的研究表明在薄层样品中也可以通过面内电流对CCDW-NCCDW 相变进行连续调控[107].

图6 二维体系中的CDW 调控研究 (a) 1T-TaS2 中电脉冲诱导金属镶嵌相的STM 图像,插图为金属镶嵌相中CCDW 的David星构型,未发生过改变[101];(b) 光脉冲使1T-TaS2 在CCDW 和隐藏态之间切换,插图为实验装置的示意图[104];(c) 1T-TaS2 中部分吸附水分 子层的STM 图像,插图为STM 图像的傅里叶变换,存 在和3×3 两种CDW 周期[109];(d),(e) 单层的NbSe2/双层石墨烯和NbSe2/SrTiO3 的STM 图像[122]Fig.6.CDW manipulation in 2D system:(a) STM image of metallic mosaic phase induced by voltage pulses in 1T-TaS2.Inset:unchanged David-star formation in CCDW of metallic mosaic phase[101].(b) Switching between CCDW and hidden state induced by optical pulse in 1T-TaS2.Inset:diagram of experimental setup[104].(c) STM image of partially water-adsorbed 1T-TaS2.Inset:Fourier transform images of STM topography showing two types of CDW periodicity including and 3×3[109].(d),(e) STM mages of monolayer NbSe2/BLG and NbSe2/SrTiO3(111) [122].

与一维体系类似,分子吸附也能对二维体系中的CDW 产生有效调控.上海科技大学的颜世超团队[108,109]利用STM 研究1T-TaS2界面的水吸附,观察到表面的水分子形成了具有6×6 超结构的单层岛,而岛下的电荷序会变得密集且无序.傅里叶变换图像表明这是3×3 与两种六角电荷序相混合的结果,dI/dV谱也说明水分子下的区域内绝缘带隙坍塌,并使得费米能级处呈现V 形带隙特征[108].此外他们还通过吸附高度有序的水分子偶极层,诱导出了新的3×3 CDW,如图6(c)所示;而除去吸附的水分子后,体系仍可恢复成局域的金属畴,这些畴被残留的水分子团簇所钉扎[109].

除上述对一维与二维材料都适用的手段,在二维材料体系中还存在着一些独特的调控方式,比如通过层厚来改变来影响层间范德瓦耳斯作用的强度,进而实现对CDW 的调控.维度的降低可以增强Peierls 不稳定性和电声子耦合,但与此同时低维体系中的无序和热涨落效应也会破坏CDW 的长程相干性[1].1T-TaS2在冷却过程中的CCDWNCCDW 相变温度随层厚的降低而降低,升温时的相变温度则略微升高,并在层厚较低时存在更大的回滞[107,110].而在二维极限下,1T-TaS2中的CDW表现受样品质量影响很大.对于机械剥离制备的1T-TaS2薄层,其输运测量的结果表明CCDWNCCDW 相变最低在2—3 nm 以下消失[107,111,112].Sakabe 等[113]在无衬底的条件下利用扫描透射电子显微镜观察了机械剥离制得的1T-TaS2薄层,发现三层TaS2的CCDW 可以在室温下存在,而在双层和单层TaS2中CDW 波矢的三次对称性被打破,且单层TaS2具有新的三斜条纹CDW.之后国家纳米科学中心的谢黎明团队[110]通过化学气相沉积(chemical vapor deposition,CVD)在h-BN上合成了TaS2薄膜,并通过拉曼光谱在单层和少层中观察到了稳定的CCDW-NCCDW 相变.清华大学的季帅华团队[114]则通过MBE 生长了单层TaS2,STM 实验显示其在低温下具有与体相相同的CCDW.而1T-TiSe2在二维极限下TCDW和CDW 带隙明显增大,从块体的三维各向异性CDW转变为二维CDW[115,116].对单层TiSe2的ARPES研究发现了激子凝聚机制驱动CDW 相变的证据[117].之后的STS 研究则通过单层中激子结合能的增大解释了TCDW和CDW 带隙大小的变化,不同介电性质的衬底能够进一步改变激子结合能,可以解释TCDW对于衬底材料的强烈依赖[118].此外也有理论研究发现单层TiSe2的声子模式在M点处存在最小值,说明其中的CDW 可以通过声子不稳定性来解释[119].对于单层VSe2,ARPES 测量和理论分析表明其二维性质使得费米面嵌套变得完美,使TCDW显著提升,并破坏了原有对称性,出现不同于体相4×4 CDW 的CDW[71,72].

而材料所处的环境也会对CDW 产生不同的影响,西北工业大学黄维团队[120]发现在石墨烯/2H-NbSe2异质结中,石墨烯的存在使CDW 的转变温度显著降低,并诱导出反常的短程CDW.第一性原理计算表明界面电子掺杂阻止了晶格畸变,进而对CDW 态产生抑制.Yeom 团队[121]的STM研究发现2H-NbSe2中Se 空位和Nb 插层两种固有缺陷能够选择性地诱导出不同的CDW 结构,分别以空位和Se 原子为中心,可以由缺陷引起的局部应力场解释,这为缺陷和CDW 相互作用提供了清晰的微观机制.此外衬底对二维材料的CDW 也存在明显的调控效应.南京大学的张翼团队研究了不同衬底对单层1H-NbSe2薄膜中CDW 的影响,发现不同基底和薄膜间的电荷转移可以影响费米面的构型以及电声子耦合强度,这将导致相变温度等特征发生改变.例如以SiC 双层石墨烯为衬底的NbSe2薄膜中,同时存在着两种稳定的CDW,分别以空位和Se 原子为中心,如图6(d)所示;但当衬底为SrTiO3(111) 时,CDW 呈现短程且畸变的不均匀结构,如图6(e)所示,其中的单向畴在4.2 K 拥有更宽的U 形带隙,并在 ± 41 meV 处发现了对称的扭结;而当衬底为Al2O3(0001) 时,体系出现了电子口袋的收缩,且费米能级出现上升,这也支持了单层NbSe2中CDW 是由电声子耦合为主导的观点[122].

4 CDW 与Mott 绝缘体的关系

Mott 绝缘体[123]是指在半填充的窄能带材料中,电子间的库仑排斥会阻碍电子间的跃迁,当电子间正相关能大于能带宽度时,能带会分裂为上Hubbard 带(upper Hubbard band,UHB)与 下Hubbard 带(lower Hubbard band,LHB),并发生金属-绝缘体转变的现象.由于Mott 绝缘体是材料中电子关联效应的体现,在二维体系TaS2和NbSe2的1T相中普遍存在,而CDW 也常出现在这些相中.因此二者之间的关系便成了近些年普遍研究的问题.在1T-TaS2中,NCCDW-CCDW 相变同步伴随体系电阻的突然上升,呈现出一级相变的特征,如图7(a)所示[124].目前传统的观点认为在1T-TaS2中CCDW 态与Mott 绝缘体共存,Mott带隙由David 星中心未配对的电子原位库仑排斥所导致[96,125].而近年的研究表明CDW 层间耦合导致的二聚化也对1T-TaS2的绝缘性发挥着重要的作用.北京大学的张焱团队[124]发现1T-TaS2在低温下会发生层间二聚并成为带隙绝缘体,具有强烈的层间跃迁,而在加热后体系转变为二维Mott 绝缘体,表明两种机制之间相互竞争.颜世超团队[126]则研究了1T层和1H层交替排列的4Hb-TaS2,发现其中CDW 较弱的1H层可以减小1T层间的CDW 耦合,同时1T层和1H层间的弱电子杂化会使1T层中的窄带略高于费米能级,从而抑制电子关联诱导的能带分裂.由于4Hb-TaS2与块体1T-TaS2具有不同的电子态空间分布,如图7(b)和图7(c)所示,表明了块体1T-TaS2的绝缘带隙来源于二聚层中窄带重叠形成的成键带和反键带[126].皮秒激光脉冲可以使CCDW 相的1T-TaS2发生可逆的金属-绝缘体转变,诱导出不同于绝缘相的金属隐藏态[103].这种金属隐藏态在垂直方向上的电荷序和轨道序发生了明显的重排,说明了层间二聚化对于绝缘性具有关键作用[127].通过STM 的针尖施加电压脉冲可以在CCDW 相的1T-TaS2中诱导出一种金属镶嵌相,金属镶嵌相中最上层的CCDW 未发生改变,但相对下一层的相位发生明显移动,这也表明堆叠顺序对绝缘性有着直接影响[101].而要彻底排除CDW 层间耦合的影响,研究单层1T-TaS2是很好的方式,季帅华团队[114]发现MBE 生长的单层1T-TaS2在低温下具有与体相相同的CCDW 和0.45 eV 的Mott 带隙,UHB与LHB 都位于David 星中心,表现为单纯的二维Mott 绝缘体.而1T-TaSe2块体在室温下具有与1T-TaS2相同的CCDW,却表现出明显的金属性,在进入二维极限后,Chen 等[128]发现电子关联可以诱导出Mott 绝缘态,并伴有异常的轨道结构.同时层间耦合会对绝缘相产生抑制,在双层和三层1T-TaSe2中,Mott 带隙减小,轨道结构消失,这能为研究强关联物理提供可有效调控的平台.

图7 CDW 与Mott 绝缘体的关系 (a) 1T-TaS2 中电阻和CDW 相随温度的变化,插图为CCDW、三斜CDW、NCCDW、ICCDW 的示意图[124];(b),(c) STM 测量的1T-TaS2 和4Hb-TaS2 中dI/dV 谱的空间分布,插图为1T-TaS2 和4Hb-TaS2 结构的示意图[126];(d) 单层1T-NbSe2 的STM 图像,UHB 的分布 相对CDW 有R30°的超结构[132];(e) 单层1T-NbSe2 中电 荷转移绝缘体示意图[99];(f) STS 测量的单层1T-NbSe2 的dI/dV 谱[99]Fig.7.Relationship between CDW and Mott insulators:(a) The changes of resistivity and CDW phase with respect to temperature in 1T-TaS2,where the insert is the diagram of CCDW,triclinic CDW,NCCDW and ICCDW[124].(b),(c) Spatial distribution of dI/dV spectrum of 1T-TaS2 and 4Hb-TaS2 measured by STS.Insets are diagrams of their structure[126].(d) STM image of monolayer 1T-NbSe2.The distribution of UHB shows R30° superstructure with respect to CDW[132].(e) Diagram of charge transfer insulator in monolayer 1T-NbSe2[99].(f) dI/dV spectrum of 1T-NbSe2 measured by STS[99].

而在NbSe2中,通过引入缺陷[129]、热处理[130]或MBE 等方法能获得1T相.研究发现MBE 生长的1T-NbSe2单层中存在的CDW,并可以观察到0.4 eV 的Mott 带隙[131].北京理工大学的王业亮团队[132]通过STM 对单层1T-NbSe2岛的研究发现,UHB 的分布远离David 星的中心,并展现出R30°重构,如图7(d)所示;而Mott 带隙中也存在类似CDW 的超晶格特征,说明CDW 与哈伯德带分离.此后王业亮团队[133]研究了单层1T-NbSe2与1H-NbSe2之间的界面电子结构,发现H相的金属态可以穿透界面,并展现出二维CDW 的近邻效应.在界面处还会出现由电子掺杂引起的Mott 带隙的崩塌,并伴随着UHB 的消失,这说明不同电子关联体系之间的相互作用可以有效调节Mott 绝缘态.而华中科技大学的付英双团队[134]发现单层1T-NbSe2中存在两种不同的David 星图案,二者可随温度变化而相互转换,并存在一定的偏角.由于层间耦合的存在,双层1TNbSe2中会出现Mott 带隙的坍塌,表明单层1TNbSe2中的绝缘机制也有可能是电荷转移带隙.此后施至刚团队[99]利用STS 发现单层1T-NbSe2中局域化的UHB 位于绝缘带隙之上,而LHB则低于价带最大值并与价带合并,如图7(e)和图7(f)所示,这一结果支持电荷转移带隙的观点.

5 CDW 与其他有序态的关系

5.1 CDW 与SDW 的关系

在一维/准一维体系中,SDW 通常存在于具有费米面嵌套或电子-电子相互作用的巡游磁性系统.例如(TMTSF)2PF6,(MDT-TTF)2Au(CN)2,(DMET)2Au(CN)2等有机材料都具有非公度的SDW[1].而在(TMTSF)2PF6中还存在一个 2kF波矢的电荷空间调制,这暗示了体系中可能存在SDW 与CDW 的混合态[135].理论计算表明二者的共存来自于相邻原子间的库仑排斥,并且共存态中的CDW 会随着库仑作用能的变化产生2kF与4kF间的竞争[136].而(TMTSF)2PF6在高压下会呈现出超导特性[137],在临界点附近0.8 kbar (1 bar=105Pa)宽的压力范围内可以观察到SDW 畴和超导畴共存,以及在不同方向上输运性质差异性的演变过程[138,139].

而对于CDW 和SDW 之间的关系,早期的研究主要集中在一些高温超导体系中,研究发现CDW与SDW 有着体系依赖的复杂关系,在某些体系中CDW 与SDW 之间是相互不公度的,且无法共存[140];而在另一些体系中CDW 与SDW 是可以相互公度的,此时QCDW2QSDW,其CDW 以非公度的条纹相形式存在,并可与超导共存[141,142].这种研究为揭示高温超导材料中的物理机理提供了重要的依据.而在二维材料中,体系中存在的较强电子相互作用使得SDW 与CDW 能够共存.例如Cr单晶材料为体心立方结构,在Γ点和H点分别有呈近八面体的电子口袋和空穴口袋,二者相互嵌套,由于空穴口袋略大于电子口袋,因此存在着两种嵌套的波矢:Q±2π/a(1±δ),从而产生波矢为QSDW2πδ/a的非公度SDW.能带上的电子Bloch态会与空穴Bloch 态相互耦合,打开带隙并降低费米面处的态密度,从而使SDW 变得稳定[143].此外在Cr 单晶中也有CDW 被发现[144],由于CDW 周期是SDW 周期的一半,通常认为CDW 是SDW的二次谐波,对应于Γ点处的嵌套波矢,其波矢之间的关系满足QCDW2QSDW[145].

Hsu 等[146]观察了W (110) 衬底上生长的不同厚度的Cr (110) 纳米岛,发现CDW 波长会随层厚的降低而逐渐增加,这可能是由于SDW 波矢的旋转所导致.而当层厚在3.7 nm 至5.2 nm 之间时,CDW 和SDW 的调制消失,这可能来源于SDW节点在表面附近的钉扎[146].而中国科学技术大学的封东来团队[147]通过自旋极化扫描隧道显微镜,首次在实空间观察到了Cr (001) 表面的SDW,并发现波矢沿[100]或[010]方向,在相邻台阶间出现反相,这表明层间存在一定的反铁磁耦合.通过偏压的改变,还观察到与SDW 共存的CDW 态.dI/dV谱则表明CDW 在费米能级以下打开了一个能隙,这与常规的费米面嵌套图像不同.研究还发现CDW 与SDW 具有相同的相位分布,且二者畴结构高度相关,这一结果也支持了CDW 是SDW二次谐波的观点[147].在MBE 生长的单层VS2中,STM 研究观察到了非公度的CDW 条纹,并发现CDW 中存在横向声子模和纵向声子模的非线性耦合.且CDW 打开的带隙位于未占据态;而费米面的拓扑结构改变也表明单层VS2中的CDW 相变属于金属-金属的Lifshitz 相变;同时X 射线磁圆二色性测量发现CDW 态的总净磁化消失,表明可能有SDW 与CDW 的共存[148].

5.2 CDW 与超导的关系

CDW 和超导本质上都来源于电声子相互作用,早期对二者之间关系的研究主要集中在高温铜氧化物超导体中.研究发现在复杂的相图中,尤其是赝能隙区存在着多种有序态,包括CDW,SDW,PDW 和电子向列相等.它们与超导之间存在的相互作用对理解高温超导机理、赝能隙等物理性质起到了十分重要的作用[149,150].同时由于超导与CDW之间具有相近的能量尺度和相似的掺杂演化关系,二者之间也展现出一定的竞争关系[151].

在准一维体系中,NbSe3[152],TaS3[153],Hf Te3[154]等材料在高压下都表现出CDW 的抑制和超导态的出现等.但由于一维和准一维材料中很难构造本征的超导特性,因此CDW 与超导之间的关系在过去研究很少,而在2H-NbSe2等二维体系里,CDW与超导可以共存,并可以通过外界条件加以调控,这为研究CDW 与超导之间的相互作用提供了很好的平台.在高压下,2H-NbSe2的TCDW降低,同时超导转变温度(Tc)升高,并且在CDW 消失后基本保持不变,而在结构类似但不存在CDW 的2H-NbS2体系里,超导对压力则不敏感,说明超导与CDW 之间存在着竞争关系[155].而ARPES 的研究发现2H-NbSe2的鞍点具有最高的电声子耦合强度和最低的费米速度,在Tc之上,鞍点处存在着由CDW 导致的谱权重损耗;而在Tc之下,鞍点处则演变出最大的超导能隙,表明在某些情况下,电声子耦合体系中的电荷序也可以增强超导[156].

而一些原子的掺杂,如Li[157],Fe[158],Co[159,160]等原子插层会同时抑制2H-NbSe2中的超导和CDW.中山大学罗惠霞团队[161]发现双掺杂体系CuxNb Se2–ySy(0≤xy≤0.1)中具有与其他掺杂体系不同的S 形相图,而样品表面则出现与母相不同的2×2 公度CDW,这可能与超导的不寻常抑制有关.而通过电子辐照可以在2H-NbSe2中引入无序,Tc与TCDW随照射剂量的增加分别上升和下降.在临界剂量以上,长程CDW 的特征突然消失,同时Tc呈显著下降趋势,如图8(e)所示,X 射线散射和霍尔电阻测量则暗示体系中存在短程CDW.这一结果说明CDW 与超导之间存在某种竞争关系,但CDW 导致的电子结构重构对超导也起到一定的辅助作用[162].2H-TaS2具有3×3 的CDW[163]和0.8 K 的Tc[164],而通过Cu 原子插层[165]、无序、高压[166]都可以诱导出拱形的超导相域,并且Tc最大值都位于CDW 的临界点处.Wagner 等[165]对CuxTaS2体系的电子衍射研究则表明在Tc最大值点,CDW 波矢发生改变,CDW 的相干长度变短.中国科学院物理研究所程金光团队[166]发现施加高压时,临界压力附近CDW 的涨落大幅增强,而CDW 消失后无序散射是影响超导的主要因素.

图8 超导与CDW 的关系 (a) 1T-FexTaS2 的相图[167];(b) ARPES 测量的不同掺杂下1T-FexTaS2 的能量分布曲线,在Γ 点有电子口袋[167];(c) Cu0.08TiSe2 的STM 图像,插 图为STM 图的 傅里 叶变换[173];(d) STS 测量的Cu0.08TiSe2 中CDW 区域 和畴 壁的dI/dV 谱[173];(e) 电子辐照的2H-NbSe2 中温度-剩余电阻率相图[162]Fig.8.Relationship between CDW and superconductivity:(a) Phase diagram of 1T-FexTaS2[167];(b) ARPES-measured energy distribution curves of 1T-FexTaS2 at different doping level showing an electron pocket at Γ point[167];(c) STM topography of Cu0.08TiSe2,where the inset is the Fourier transform of STM image[173];(d) STS-measured dI/dV spectra of CDW regions and domain walls in Cu0.08TiSe2[173];(e) temperature-residual resistivity phase diagram of 2H-NbSe2 upon electron irradiation[162].

而对于其他存在CDW 但不存在本征超导的二维材料,通过适当的化学掺杂可有效改变能带结构和载流子浓度,从而对CDW 进行调控,并最终影响超导电性.中国科学院固体物理研究所孙玉平团队[167]发现在1T-FexTa1–xS2体系里,Fe 原子对Ta 原子的替换可有效抑制CCDW,而当CCDW消失后,相图中会出现最高转变温度为2.8 K 的拱形超导区域,如图8(a)所示.当掺杂浓度x高于0.04 时,体系进入安德森局域化,来源于Fe 原子的无序占据所导致的随机势场[168].该团队还利用ARPES 发现NCCDW 态中位于Γ点的电子口袋,该电子口袋是由NCCDW 超晶格势所导致的能带背向翻折所产生,并随着CCDW 与安德森局域化的形成而被破坏,如图8(b)所示,这被认为是NCCDW 与超导共存的证据[167].此后孙玉平团队[169]在1T-TaS2–xSex体系相图中观察到了与铁掺杂情况类似的拱形超导区域,最高转变温度为3.6 K,证实了超导电性并不特别依赖于Ta 原子位或S 原子位的掺杂.2016 年该团队[97]还通过理论计算发现,在1T-TaS2中电子掺杂有利于CCDW稳定,而空穴掺杂则可以抑制CCDW,当掺杂浓度高于2.6 holes/David star 时,CCDW 会被完全抑制,并预估最高可以引入转变温度为6—7 K 的超导态.

而在1T-CuxTiSe2(x<0.11) 体系中,Cu 原子的插层会使TCDW逐渐降低,并在x>0.04 时诱导出超导态,在x0.08 时有最高转变温度4.15 K;同时随着Cu 原子含量增大,材料的磁化率增大,电阻率降低,表明此时Cu 原子将载流子引入了TiSe2的导带中,增大了费米能附近的态密度[170].钱冬等[171]通过ARPES 研究,观察到L点附近的电子口袋随Cu 原子插层而发生变化,同时在x>0.04 时CDW 的长程相干性出现系统性缺失.X 射线衍射研究则在超导拱形相域上方发现了非公度CDW,其随超导的出现而产生,说明非公度CDW对超导的形成可能发挥重要作用[172].随后颜世超团队[173]的STM 研究发现Cu0.08TiSe2中存在被Cu 原子钉扎的局域CCDW 畴,畴之间有一定的相移,导致CDW 从母体相的CCDW 转变为IC CDW,解释了ICCDW 的形成机理,如图8(c)所示.图8(d)为STS 的测量结果,表明畴壁在费米能级附近会具有额外数量的费米子,这可能是超导电性的来源.

此外,通过高压也可调控电子间的相互作用,进而在不引入额外复杂度的前提下调控CDW.随着压力的增加,1T-TaS2不同CDW 态的转变温度会逐渐降低,在0.8 GPa 以上时CCDW 和绝缘态会被完全抑制,2.5 GPa 时则在NCCDW 相域内产生Tc为1.5 K 的超导态,该超导态不随高压的增大或NCCDW 向金属相的转变产生敏感的变化[95].中国科学院物理研究所王铂森等[174]还发现相对于单向压力,静水压能更彻底地抑制CDW,并且Tc还会随着静水压强的升高呈现单调上升趋势,可能由于两种压力下体系的电子结构与声子谱的演变方式存在一定的差异.但对1T-TiSe2体系施加高压后,出现的则是2—4 GPa 的拱形超导区域,同时CDW 对应的输运特征也会逐渐变弱并在3 GPa时彻底消失[175].此后X 射线散射研究则在3 GPa附近观察到了非公度的CDW,表明超导的形成可能与CDW 畴壁的建立有关[176].上海技术物理研究所的戴宁团队[177]发现4 GPa 时体系发生了一级结构相变,说明超导相变与结构相变之间也存在一定关系.近年Lee 等[178]构建了1T-TiSe2体系中高压和Cu 原子插层的完整相图,发现最高转变温度钉扎在CDW 的量子临界点上,这说明超导与CCDW 有很强的相关性.而程金光团队[179]利用高压和插层同时调控,表明了CDW 涨落在超导配对中的重要性,以及CDW 坍塌对费米面重构的影响.

而在二维材料中,随着层厚的改变,CDW 和超导之间的关系也会发生相应的变化.奚啸翔等[180]发现在二维极限下2H-NbSe2仍有超导相与CDW共存,并且CDW 会显著增强,TCDW可以由体相的33.5 K 增大到单层的145 K.其拉曼光谱的实验也发现存在明显的蓝移趋势,这说明在二维极限下NbSe2的电子-声子相互作用会显著增强.同时Tc则随着层厚的减小而降低,从块体的7.2 K 降至单层的1.9 K[87].清华大学段文晖团队[181]通过第一性原理计算表明,随着2H-NbSe2层厚的减小,能量增益的上升和费米面能隙的扩大增强了CDW态,并使得费米面处的态密度降低,导致超导性减弱.而2H-TaSe2的情况则有所不同,北京大学张艳锋团队[182]通过CVD 在金箔上生长了单层1HTaSe2薄膜,发现单层中的3×3 CDW 明显增强,TCDW从体相的90 K 增加到125 K.Wu 等[183]的电输运测量则发现3 nm TaSe2薄层的Tc从块体的0.14 K 提升到了1.4 K 以上.段文晖团队[184]的理论研究证明单层TaSe2中的本征电声子耦合强度极大增强,克服了CDW 增强导致的费米能级态密度降低和低维下变强的库仑排斥,从而使超导电性提升.该工作首次揭示了二维极限下CDW 与超导同时增强的机理.

在近期热门的Kagome 晶格层状材料AV3Sb5(A=K,Rb,Cs)中也有着CDW 和非常规超导等物理性质,可以为研究电子关联效应、能带非平庸拓扑和几何挫折之间的相互作用提供一个新的量子平台[69].M点处的鞍点嵌套[81,80]和电声子耦合[185,186]都被认为在AV3Sb5的CDW 形成过程中发挥了重要作用.其中CsV3Sb5的Tc在2.3 K 左右,在Tc之上具有2×2×2 周期[187]或2×2×4 周期[188]的CDW,对应于94 K 处电阻率的扭结和热容的尖峰,并呈现一级相变的特征[189].超快泵浦探针测量发现CsV3Sb5在相变时没有明显的声子软化,这一结果也证明其是弱的一级相变,而CDW 态中振幅模式的缺失也与传统的CDW 凝聚有着很大不同[190].陈仙辉团队[191]与程金光团队[192]各自独立发现在CsV3Sb5中,随着CDW 被高压抑制,Tc对压力的依赖呈现出与传统拱形相域不同的双峰表现.两峰之间超导的抑制伴随着量子振荡的快速衰减,剩余电阻率的突然增大和磁阻的快速减小,说明材料中可能形成了新的CDW 态;而Tc的第2个尖峰在CDW 消失时出现,则表明CDW 与超导之间存在着不寻常的竞争机制.近期陈仙辉、吴涛、王震宇团队[193]还在CsV3Sb5中发现了CDW驱动的电子向列相,为理解CDW 与超导的反常竞争提供了新的见解.在RbV3Sb5中程金光团队[194]则观察到浅M 形的超导相域,表明CDW 与超导的竞争较弱,可能与RbV3Sb5层间距离相对较小有关.Qian 等[195]发现对CsV3Sb5施加沿a轴的单向应力可以提高Tc并降低TCDW,并且在以c轴晶格常数为变量时与高压实验的Tc和TCDW变化保持一致,表明c轴晶格常数的变化是影响CDW 与超导竞争的主要原因.进一步的理论研究则指出c轴晶格常数会影响CDW 序参量与M,L点波矢的耦合,从而对CDW 产生抑制.中国科学院物理研究所陈小龙团队[196]还发现CsV3Sb5薄片中CDW 被抑制,超导则得到增强.而通过顶层Cs 原子的选择性氧化可以实现对体系的空穴掺杂并引入拱形超导,且Tc在费米能级与高阶鞍点重合时达到最大值.同时TCDW也明显降低,可以由高阶鞍点较弱的嵌套特性来解释.

5.3 CDW 与PDW 的关系

PDW 是材料在超导状态时具有的一种新的基态,与CDW 有密切的关系,最早在铜氧化物等强耦合超导体系中发现.在理论上,PDW 被描述为超导序参量随实空间周期性调制的物理图像,而在实验中则表现为库珀对态密度以及超导能隙在实空间中的周期性变化[197].除此之外,PDW 体系被预言存在由对称性决定的次级序,其中CDW 为最主要的一种,实验观测PDW 与CDW 共存及其伴生现象对理解PDW 形成的微观机制具有重要作用[198].在2016 年,Hamidian 等[199]运用扫描约瑟夫森隧穿显微术(scanned Josephson-tunneling microscopy,SJTM),首次直接观察到铜氧化物中库珀对密度调制的 PDW 现象,同时还发现其与波矢相同的CDW 共存.之后Du 等[200]在超导针尖增强的隧穿谱中观察能隙随实空间的周期性变化,并在赝能隙偏压附近观察到了波矢为QP(0.25 倍晶格常数)和 2QP的两套电荷密度调制,证实了理论上PDW 与超导耦合所导致两个不同周期CDW的产生.此外,Edkins 等[201]在涡旋附近也发现了两套电子态调制,波矢同样为QP和 2QP,后者的调制振幅从涡旋中心衰减的速度是前者的两倍,符合Dai 等[202]提出的理论模型,从而指出PDW 与d 波超导存在的竞争关系.

除了铜氧化物,在CDW 与超导共存的TMD材料体系中也发现存在PDW.刘晓龙等[203]通过SJTM 在2H-NbSe2中探测到了库珀对态密度与带隙随CDW 波矢的空间调制.在CDW 公度畴和非公度畴壁附近,PDW 复制了CDW 的相位分布并有 2π/3 的相位差,进而说明PDW 有可能来源于与CDW 与超导的耦合.

随着新型二维材料的出现,中国科学院物理研究所高鸿钧团队[204]在Kagome 晶格材料CsV3Sb5中也发现了PDW,其超导相干峰高度和带隙的4a/3 双向调制,被认为与潜在的涡旋-反涡旋晶格有关,中国科学技术大学王震宇等[187]也观察到了类似的现象.对于CsV3Sb5体系的CDW,中国科学院理论物理研究所的周森等[205]通过理论研究指出,在Kagome 晶格的van Hove 填充附近,2×2的CDW 可以形成Chern 费米口袋,而产生的Chern费米口袋具有较大的Berry 曲率,轨道磁矩和霍尔电导,并可以由4/3 布拉格波矢相连接,从而产生实验观察到的4a/3 的PDW 调制.

目前有关PDW 的研究还处于起步阶段,其与CDW 之间的具体关系目前还在研究中.如铜氧化物中CDW 可以作为PDW 与超导耦合产生的二级序,对于传统2H-NbSe2体系,CDW 也可以独立于PDW 存在.两者的具体微观作用机制还有待进一步的实验数据以及理论分析.

6 二维体系中的CDW 的激发

一维材料中CDW 的激发态已成为研究热点,而在二维CCDW 体系中也存在与一维情况类似的孤子激发,如1T-TaS2的电导同样在低温下展现出对电场的非线性依赖关系[206].天津理工大学马永昌等[207]研究了50 K 以下1T-TaS2的极化性能和输运性质,发现样品在107Hz 下具有约104的极大介电常数,这认为其不能由局域载流子跃迁所解释,并且发现直流偏压可以对介电常数进行抑制,这说明非线性电导可能由束缚孤子-反孤子对离域导致.此外由于二维体系所具有的丰富特性,CDW 的激发可以表现出多种形式,并与其他激发共存且相互耦合.在1T-TaS2的NCCDW 态中,Altvater 等[208]的开尔文探针显微镜研究发现了一系列涡旋状的拓扑激发,并通过计算CDW 涡旋的空间关联函数发现这些拓扑激发形成了准长程序,与II 型超导体中的布拉格玻璃态类似.而由于带间跃迁的固有屏蔽效应,二维材料中等离激元有着平坦的共振频率分布,复旦大学晏湖根团队[209]发现2H-TaSe2中的等离激元对层厚和介电环境很敏感,且等离激元和CDW 激发之间存在一定的耦合效应,靠近CDW 激发频率的等离激元峰出现了峰高和线宽随温度非单调变化的现象.

而对称性自发破缺体系中普遍存在相位模式和振幅模式两种集体激发,在超导体中的振幅模式由于其性质与粒子物理学中的Higgs 玻色子相似,被称为Higgs 模式.作为能量最低的集体激发模式,Higgs 模式在超导体中占有特殊的地位,但由于其是序参量的标量激发,并不与电磁场线性耦合,且具有与超导带隙相同的能量尺度,以前一直很难被实验观测到[210].但在超导与CDW 共存的2H-NbSe2体系中,CDW 的振幅模式与Higgs 模式相互耦合,从而允许通过拉曼光谱间接探测Higgs模式.最早在1980 年,2H-NbSe2的拉曼光谱在Tc以下观察到一个新的峰值,并且施加磁场可以抑制新模式的强度,同时增强CDW 的振幅模式[211],之后这种新观察到的超导模式被确定为是Higgs 模式[211,212].而近年的拉曼研究发现,在不具备CDW的2H-NbS2体系中,只能观察到更弱的库珀对断裂模式,不存在与2H-NbSe2类似的窄而强的超导模式,表明了CDW 对观测Higgs 模式的必要性.而在NbSe2进入超导态后,光谱权重从CDW 振幅模式向Higgs 模式发生了转移,如图9(a)所示,说明Higgs模式的拉曼强度全都来自与其共存的CDW 振幅模式[213].施加4 GPa 以上的静水压可以使CDW被完全抑制,Higgs 模式尖峰也一并消失,只有更弱的库珀对断裂峰还存在,进一步证明了Higgs 模式与CDW 的关系[214].在另一种CDW与超导共存的体系2H-TaS2中,高压也对Higgs模式与CDW 有着类似调制,并且带隙内的Higgs模式和非相干库珀对断裂峰出现更清晰的分离[215].

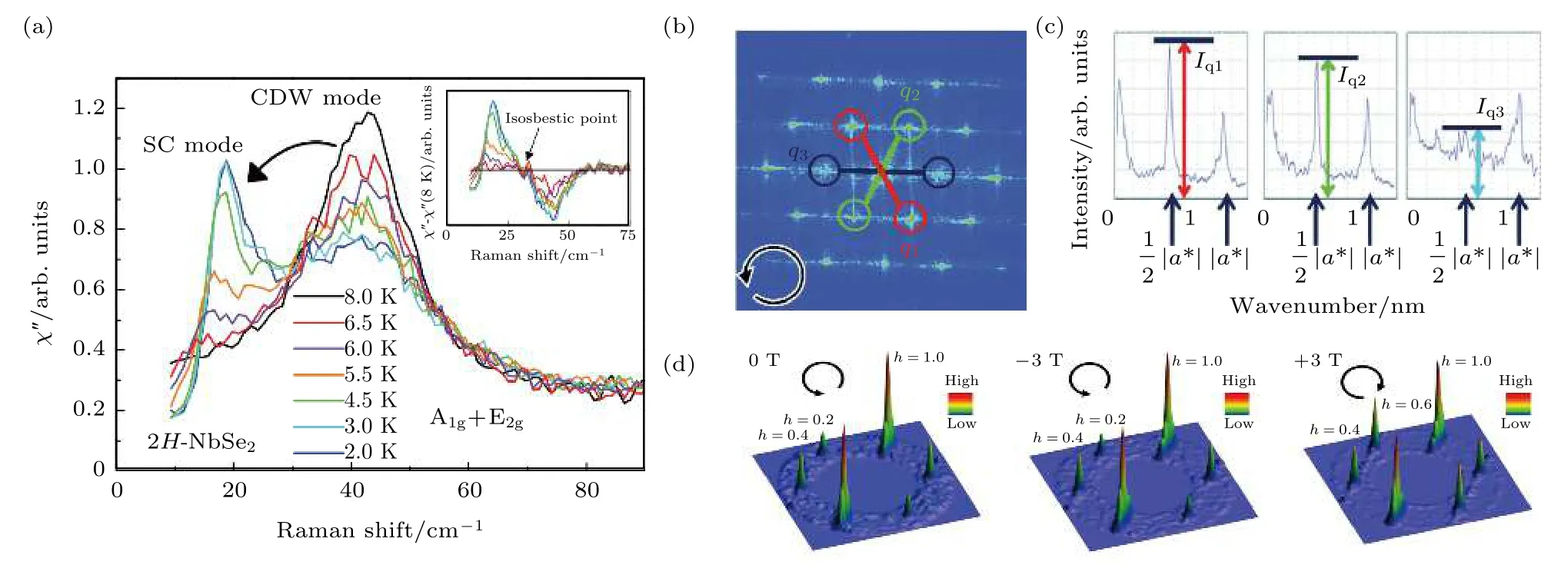
图9 (a) 2H-NbSe2 中拉曼谱的CDW 模式和超导模式随温度变化,进入超导态后谱权重从CDW 模式向超导模式中转移,插图为减去8 K 测量数据后的拉曼谱[213];(b) 1T-TiSe2 中STM 图像的傅里叶变换[216];(c) 图(b)中沿3 个波矢方向的线截面[216];(d) STS测量的不同磁场下RbV3Sb5 中dI/dV 图的傅里叶变换[223]Fig.9.(a) Changes of CDW mode and SC mode of Raman spectra with respect to temperature in 2H-NbSe2 with spectral weight transfer from CDW mode to SC mode when going into SC state,inset:Raman spectra subtracted from the data measured at 8 K[213];(b) Fourier transform of STS-measured dI/dV map in 1T-TiSe2[216];(c) line profiles along three wave vectors of figure (b) [216];(d) Fourier transform of STS image in RbV3Sb5 at different magnetic field[223].

7 手性CDW

手性是指系统通过任何平移或旋转都不能与其镜像重合的特性,是一种基础的对称性破缺形式.在具有矢量序的SDW 中,手性是一种常见的性质[6],而作为标量序的CDW 中,手性则较难出现.1T-TiSe2是最早被发现具有手性CDW的体系,其在200 K 下会发生CDW 相变,形成具有2×2×2 超结构的公度CDW[88],而在更低温度下,由于其沿面内3 个方向的CDW 分量具有不同的强度,如图9(b)和图9(c)所示,从而存在两种手性相反的螺旋堆垛方式,并导致体系出现三重对称性破缺,因此被称为手性CDW.在光学偏振测量中则表现出对应于两种手性的双重对称性[216].此后的理论研究还发现轨道序会伴随手性CDW一并出现[217].而北京大学彭莹莹等[218]通过共振X 射线散射研究,观察到了Ti 原子d 轨道之间存在长程轨道序,并发现轨道序与自旋、电荷分布和晶格自由度之间有很强的相互作用,证明了轨道序在TiSe2中的重要作用.Xu 等[219]通过光学手段实现了对手性CDW 的调控,在1T-TiSe2上照射中红外圆偏振光并将其冷却到临界温度以下,可以导致一个手性畴优先形成,这为实现和控制其他量子材料中的手性电子相提供了重要的方向.

孙玉平团队[220]在Ti 原子掺杂的1T-Ti0.08Ta0.92S2中也观察到了异常的手性CDW 基态,该材料保留了1T-TaS2中的扁平带和CCDW 结构.但由于David 星具有特殊的排列方式,其相邻畴的排列方向之间相差一定的角度,从而呈现出手性特征.该特征可能由掺杂增强的轨道序导致,说明引入具有强轨道特性的元素有可能诱导出CDW系统中的手性电荷序,这为手性CDW 材料的研究开辟了新的途径.

Kagome 超导体AV3Sb5(A=K,Rb,Cs)中存在2×2 的公度CDW.Jiang 等[221]发现KV3Sb5的磁场响应在2×2 波矢处有具有显著的增强,并呈现出手性各向异性,由于CDW 波矢连接了M点处的鞍点,并在附近的Dirac 锥处打开拓扑能隙,从而引入较大的Berry 曲率,因此KV3Sb5中存在的具有轨道磁性的巨大反常霍尔效应很可能来源于手性CDW;并且CDW 的手性会随外加磁场的改变而改变,当磁场由+2 T 变为–2 T 时,手性由顺时针变为逆时针,说明存在时间反演对称性破缺.在CsV3Sb5中,北京理工大学姚裕贵团队[222]观察到了2×2 的CDW 和1×4 超晶格的共存,其中2×2 的CDW 的振幅和所打开能隙的大小呈手性各向异性调制,并且沿1×4 超晶格波矢方向的向量峰最强,表明两种电荷有序之间存在相互作用,而在缺陷较多的表面则基本不存在手性.Shumiya 等[223]在RbV3Sb5的Sb 表面也观察到了2×2 的手性CDW 与1×4 超晶格,当磁场由+3 T 变为–3 T 时,手性由顺时针变为逆时针,如图9(d)所示,并且主要在较高能量处发生改变,而在缺陷较多的区域出现了类似的手性减弱和强磁场响应的缺失.

8 总结与展望

CDW 的研究起源于一维材料,但随着材料制备和测量技术的发展,CDW 的研究已拓展至二维材料,尤其是以过渡金属四五六族(Ta,Nb,V等)元素为基础的材料.通过前面的综述可以看到,一维CDW 的大部分物理性质在二维材料中仍存在,但其表现形式和产生机理与一维材料有所不同;但基于二维材料丰富的光学、磁学和超导性质,CDW 与其耦合产生的效应为CDW 的物性研究领域提供了很多新方向,极大程度拓展了CDW 的调控手段,这为未来开发更多基于二维功能材料和器件奠定了基础.而随着对不同二维材料CDW 性质差异性的深入研究,也会对CDW 基本物性的理解和物性调控手段的拓展提供更多思路.

由于二维材料的层间多为范德瓦耳斯作用,在应用时对环境的依赖性小,不易被破坏.而一维材料中具有的强电声子耦合和电子关联效应可以使CDW 的调控更加精准,这促生了将TMD 材料制备成一维/准一维材料的研究.传统二维材料中存在的一维线缺陷由于制备时具有随机性,在未来器件应用价值有限.因此近些年一维TMD 纳米链可控诱导生长方法[224]将为CDW 在这种准一维TMD材料中的研究提供重要的材料.

除了一维材料制备,近些年发展的叠堆二维功能材料也为人工构造的功能性异质结提供了重要的研究方向.在传统的层状超导中,如铜基高温超导材料,电荷序对超导性质影响很大.而原子层间晶格可能因畸变导致CDW 产生巨大差异.因此选择不同的叠堆材料并调控材料间的晶格匹配,有望实现人工调控的CDW.而近些年发展的有机插层准二维材料,可有效避免衬底对材料性质的影响,为未来探索本征二维CDW 提供重要的方法.由于CDW 本身具有结构和电荷的周期性调制,在CDW表面可以实现原子纳米线[225]或分子超晶格[226]的吸附自组装.而二维材料中的CDW 态可以通过多种手段进行调控,这为应用于纳米器件提供了可能,如利用低温下1T-TaS2的金属-绝缘体转变,可以制作有高开关比的场效应晶体管[111]、非易失性存储器[227]等.室温下1T-TaS2薄层可以在NC CDW 和ICCDW 之间来回快速可控切换,这有望应用到电压振荡器[228]等电子器件中.而一些材料中的CDW 被发现具有多带性[229]和拓扑性[230],这为未来CDW 调控的量子计算提供一种可能的思路.但目前对于二维材料中CDW 产生的物理本质和起源等问题依然存在较大争议.当然在传统的一维材料中,CDW 的起源、相变时结构和电子态的关系及调控、拓扑激发的性质判定等问题也仍有很多问题没有能够完美解决.而二维材料中复杂的晶格结构特征、不确定的电子关联作用以及多耦合的物理性质也使得CDW 的机理探索变得更为复杂.从目前的实验可以看到,绝大多数的二维材料还很难给出确定的能隙值和CDW 的物理性质.尤其是在衬底、维度以及缺陷等影响下,很难得到二维材料CDW 性质的普适结果.但相信随着科学技术的进步,未来会有更多的研究来揭示二维材料中CDW 的性质,拓展CDW 在各种体系中的应用.