(3+1)维修正KdV-Zakharov-Kuznetsov方程的行波解*
2022-07-19王双特于恒国
王双特 于恒国
(1. 温州大学 数理学院, 温州 325035) (2. 乐清市柳市镇第三中学, 温州 325604)
引言
Zakharov-Kuznetsov(ZK)方程作为理论物理学中研究非线性波的一类重要方程,首先由Zakharov和Kuznetsov利用磁化等离子体的流体描述得到, 此后Shivamoggi等人也得到了ZK方程[1-3].一般地,具有幂律n非线性(3+1)维Zakharov-Kuznetsov方程为
ut+αunux+(Δa1,a2,a3u)x=0
(1)
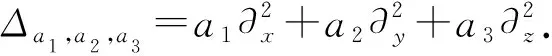
对于n=1,当Δa1,a2,a3=Δ(Laplace算子)时,文献[4]利用Extended Simplest Equation法讨论了一类行波解,文献[5]利用F-展开法获得了其它方法不曾给出的形式更丰富的显式行波解,包括双曲函数解和三角函数解;当a1=b,a2=a3=1时,文献[6]应用经典李群方法得到了其对称和约化方程,通过求解约化方程给出原方程的一些精确解;当α=6,a1=1,a2=a3=3时,文献[7]提出了Wronski形式展开法,通过该方法求出了双孤子解、双三角函数解、Complexiton解、Matveev解和Jacobi椭圆函数解;当α=1,Δa1,a2,a3=Δ时,文献[8]证明了相应初值问题解的指数衰减性,同时指出这个性质与加权Sobolev空间中解的持久性及解的唯一连续性相关;而文献[9,10]则解决了Δa1,a2,a3=bΔ时可能的行波解.此外文献[11,12]也进行了深入研究.
对于n=2,当Δa1,a2,a3=Δ时,文献[13]将其转化为复域中的常微分方程(ODE),并给出相应亚纯行波解;文献[14](Δa1,a2,a3=Δ)基于交换代数除法定理,给出了若干首次积分及对应行波解.对于n为正整数,文献[15,16]结合动力系统分支理论讨论了一些行波解,但都取积分常数为零.
基于文献[14~16],本文定性分析n=2和Δa1,a2,a3=Δ时的行波解,即(3+1)维修正KdV-Zakharov-Kuznetsov(MKdVZK)方程
ut+αu2ux+(Δu)x=0
(2)
假定上述偏微分方程(2)有行波解u=u(ξ),化为一个三阶ODE
-cu′+αu2u′+3u‴=0
(3)
(4)
注意C1为积分常数.引入X=u,Y=u′并改写X和Y为x和y,得到与式(4)等价的平面三次多项式系统
(5)
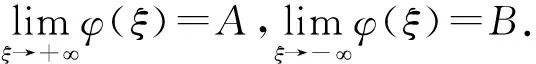
一般文献中,对于C1≠0的情形较少讨论,故本文对此进一步讨论,安排如下:首先分别研究C1=0和C1≠0时的相轨线和几类行波解;其次结合Hamilton函数法给出多模态近似解及其数值模拟;最后总结和讨论.
1 C1=0的情形
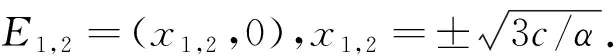
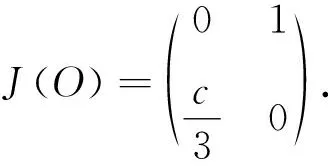
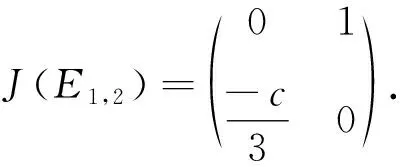
基于以上分析,分情况讨论闭轨的存在性.不妨设相轨线为
Γ(h)={(x,y)|H(x,y):=
(6)
(1)c,α>0
此时,由奇点指标可知,闭轨所围奇点仅有三种可能:{O,E1,E2},{E1}或{E2}.常数h满足h≥h0=-c2/2α(h0<0).当h0
沿同宿轨Γ(0)的行波解为
(7)
C2为积分常数.对于一般的h,沿闭轨Γ(h)的行波解形式上为Jacobi椭圆余弦函数
u(ξ)=±Acn[k(ξ+C2),m]
(8)
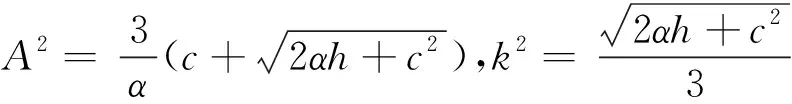
(2)c,α<0
由奇点指标可知闭轨内部只有奇点O.常数h无限制,但h0>0.当h=h0时有同宿轨Γ(h0);当0
沿同宿轨Γ(h0)的行波解为
(9)
对于h∈(0,h0),沿闭轨Γ(h)的行波解形式上为Jacobi椭圆正弦函数
u(ξ)=±Asn[k(ξ+C2),m]
(10)
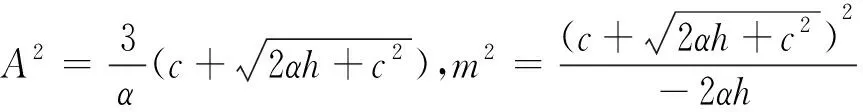
(3)c>0,α<0
此时不存在闭轨,因唯一的奇点O是鞍点.
(4)c<0,α>0
此时有一族闭轨围绕O,但h≥0.当h=0时闭轨Γ(h)退化为奇点O.同上有行波解(8).
(5)c=0,α>0
此时有一族闭轨围绕奇点O,同样h≥0.当h=0时闭轨Γ(h)退化为奇点O.通过虚模数变换可得行波解
(11)
(6)c=0,α<0
总之,在情形(1)、(2)、(4)、(5)下可有闭轨(周期解)或有界行波解.图1(a)-图1(f)描述了几种相轨线.
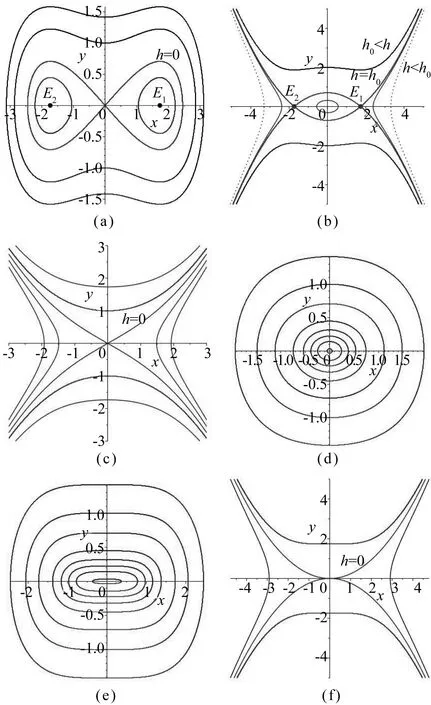
图1 C1=0时的相图:(a)c=α=1;(b)c=α=-1; (c)c=1,α=-1;(d)c=-1,α=1; (e)c=0,α=1;(f)c=0,α=-1.Fig.1 Phase diagrams when C1=0: (a)c=α=1;(b)c=α=-1; (c)c=1,α=-1;(d)c=-1,α=1; (e)c=0,α=1;(f)c=0,α=-1.
2 C1≠0的情形
此时O不是平衡点.设平衡点为E*=(x*,0),其中x*满足三次方程
(12)
(13)
以下对Δx分情况讨论.此外式(3)有首次积分
H(x,y)=fh(x)-y2=0
(14)
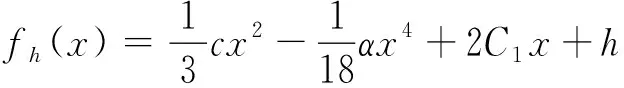
2.1 Δx>0的情形
此时方程(12)有一个实根和两个复根,且要
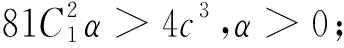
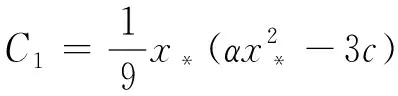
(15)
故C1与x*异号.但这不可能,因此唯一的平衡点E*是中心,有周期解.
此外,当C1>0时E*位于x正半轴上,反之则位于x负半轴上.而h有负的下限hm,利用方程组f(x)=fh(x)=0及Sylvester结式法可知,hm满足三次方程
(16)
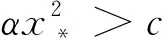
图2给出了上述几种情形的相轨线.
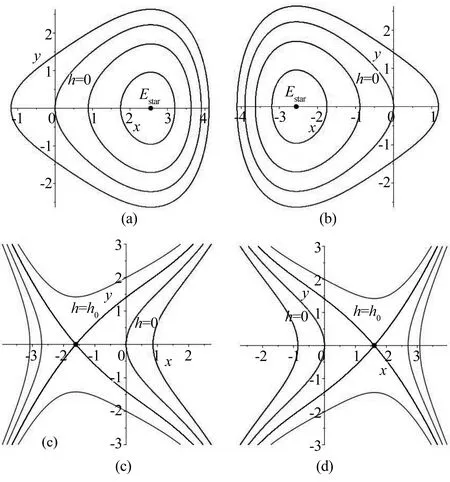
图2 Δx>0时的相图:(a)c=α=C1=1;(b)c=α=1,C1=-1; (c)c=1,α=-1,C1=1;(d)c=1,α=-1,C1=-1.Fig.2 Phase diagrams when Δx>0:(a)c=α=C1=1;(b)c=α=1,C1=-1; (c)c=1,α=-1,C1=1;(d)c=1,α=-1,C1=-1
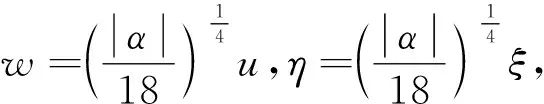
[(w-l)2+s2]
(17)
这样有界行波解形式上为
(18)
相应系数为
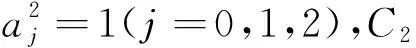
2.2 Δx=0的情形
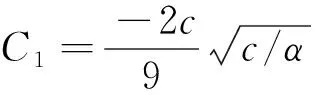
(19)
上述系统等价于[20]
x′=y,y′=x2+o(|x,y|4)
(20)
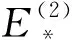
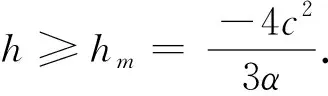
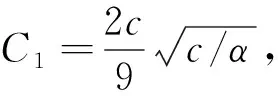
图3给出了上述几种情形的相轨线.
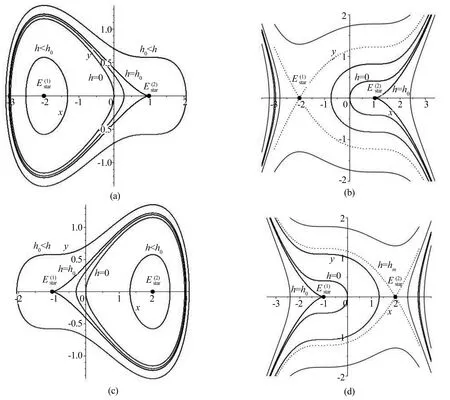
图3 Δx=0时的相图:Fig.3 Phase diagrams when Δx=0.
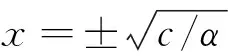
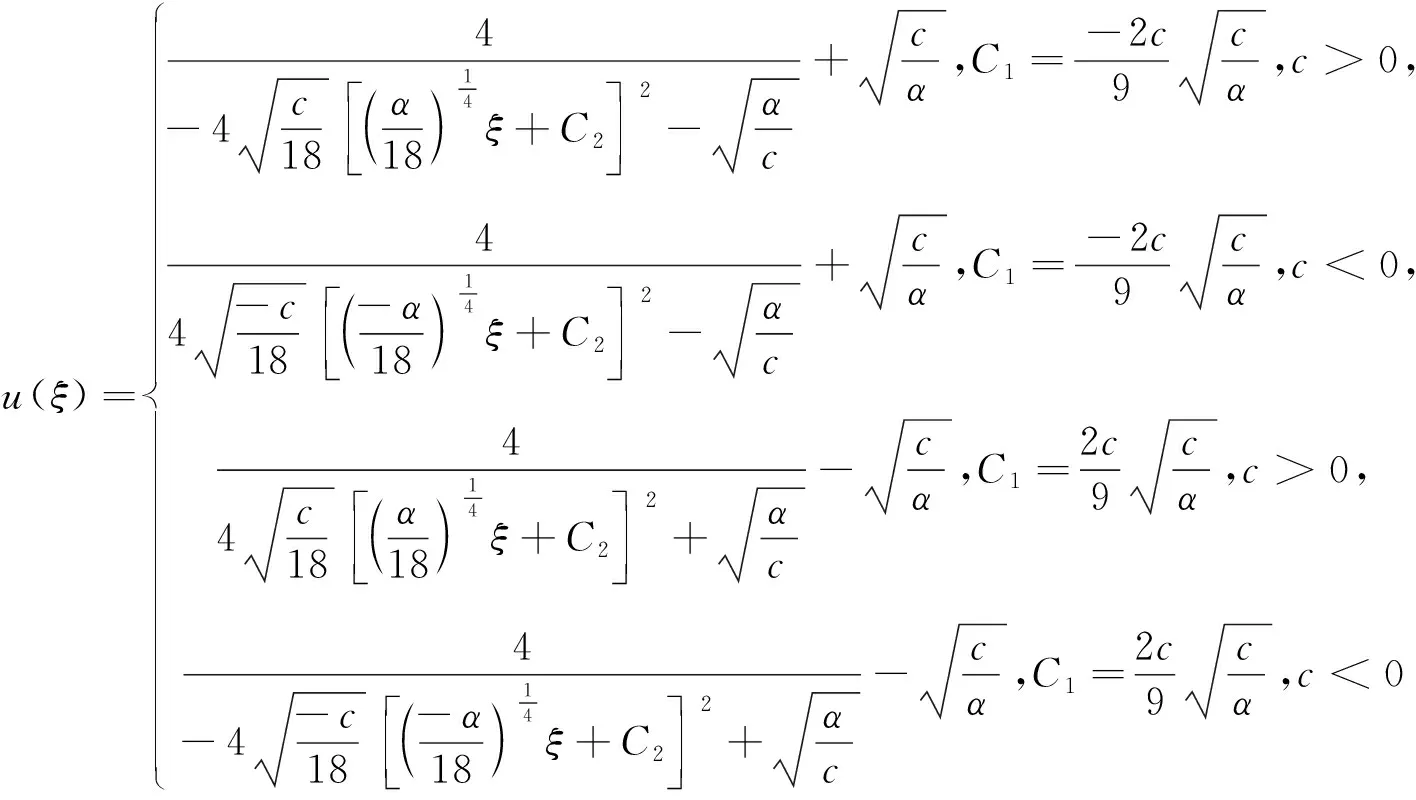
(21)
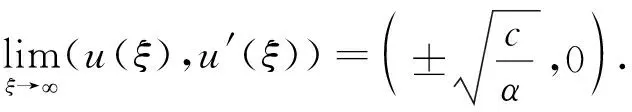
当h≠h0和hm时,有界行波解形式上同式(18).
2.3 Δx<0的情形
此时有三个两两不相等的实根,而c与α同号,只需考虑以下两种情形即可
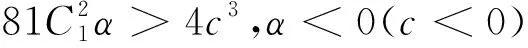
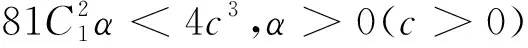
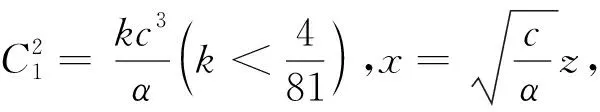
先看c>0.此时h≥hm=min{h1,h3},而h2>h1,h2>h3.但当C1>0时,作差有
(22)
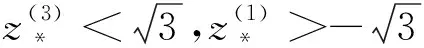
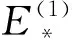
(23)
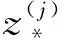
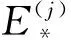
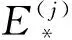
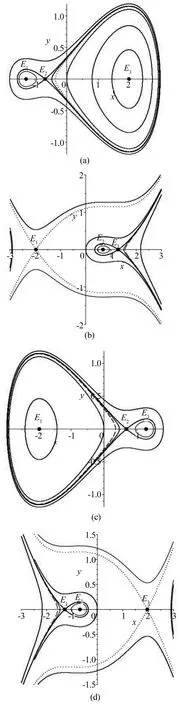
图4 Δx<0时的相图:Fig.4 Phase diagrams when Δx<0:
最后看有界行波解.同样地当h≠hj(∀j)时,fh(x)=0无重根.对于c>0,当h>h2或h∈ (hm,max{h1,h3})时,有界行波解形式上同式(18).
当c>0,h∈(max{h1,h3},h2)时,存在有界行波解.改写式(17)为标准形式
-(w-w1)(w-w2)(w-w3)(w-w4)
(24)
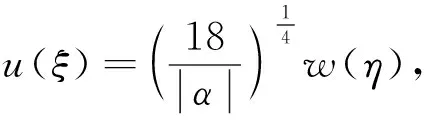
(25)
Jacobi椭圆正弦函数为
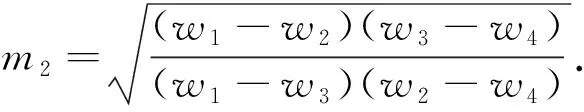
(26)
单重实根xb>xc,有界行波解形式上为
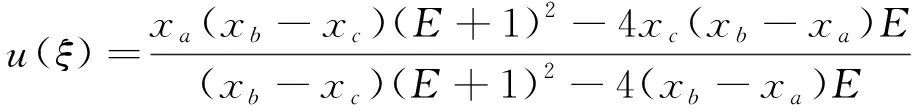
(27)
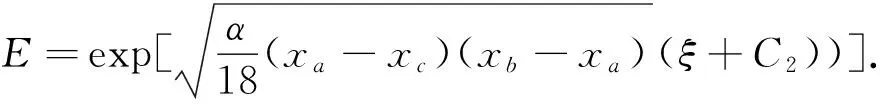
3 Hamilton函数法求多模态近似解
当奇点为中心时,文献[21]利用Hamilton函数法给出一个强非线性二阶微分方程的多模态近似解以反应周期性.以上可以看到,有界行波解或周期解常以Jacobi椭圆函数的复杂形式出现,因此需要一种近似方法来快速反应精确解.
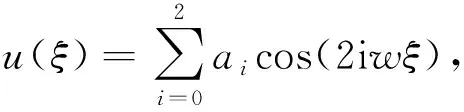
(28)
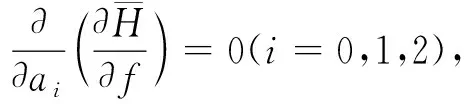
(29a)
(29b)
(29c)
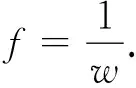
例1:取参数c=α=1及初值A=1,由方程(29)解得系数
a0= 1.554207050,a1= -0.6152063185,a2= 0.06099926808,f=2.732773277.图5(a)中分别绘出了多模态近似解(黑色实线)和解析形式解(8)(红色点线)曲线,在0≤ξ≤70内两者几乎重合,近似程度非常好.
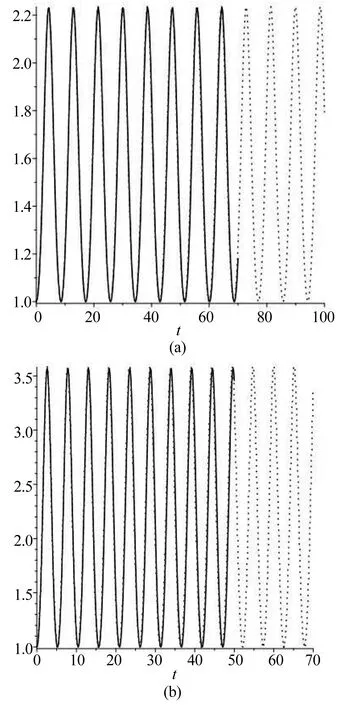
图5 多模态近似解(实线)曲线与(a)例1中解析解(点线)曲线;(b)例2中解析解(点线)曲线.Fig.5 Curves of multi-mode approximate solution(line) and(a)analytical solution(dot line) in example 1; (b)analytical solution(dot line) in example 2.
其次,以C1,α,Δx>0为例.Hamilton函数同上,类似的有代数方程组.以数值实例来说明.
例2:取c=α=k=A=1,由方程(29)解得系数
a0=2.146903270,a1=-1.284554716,a2= 0.1376514457,而f=1.665373391.图5(b)中绘出了多模态近似解(红色点线)和解析形式解(黑色实线)曲线,近似程度同样非常好.
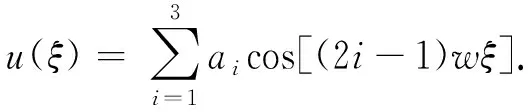
4 结论
本文主要定性分析了非线性(3+1)维修正KdV-Zakharov-Kuznetsov方程的行波解和相轨线情况.与已有文献相比,结合平衡点E*所满足三次方程的判别式,我们深入研究参数C1≠0的情形,并描述了相轨线的走向,同时形式上给出了若干有界行波解的表达式.今后,可深入研究广义ZK方程,以及高维和分数阶情形[15,16,23,24].总之,这是一个值得继续研究的方向.
