高速铁路覆冰接触网舞动行为研究*
2022-07-19施海健陈果杨翊仁杨洋
施海健 陈果 杨翊仁 杨洋†
(1.西南交通大学 力学与工程学院,成都 610031)(2.核反应堆系统设计技术重点实验室,成都 610031)
引言
接触网在一定条件下可发生低频、大幅舞动,对输电系统造成破坏.2003年2月有新闻报道了一起京广铁路接触网在强风作用下发生舞动的事故,其垂向振幅达到了1 m,造成了接触网部件的巨大损坏,严重扰乱了铁路运输秩序.因此,接触网的舞动得到了众多学者的关注.
舞动最初由Den Hartog在研究覆冰导线低频、大幅振动时提出[1],之后便引起了学术界的广泛关注.当前已有较多关于输电线舞动的研究[2-6],相关理论也相对成熟[7],而铁路接触网的舞动研究则相对较少.接触网发生舞动的一个必要条件是接触线存在磨损[8, 9].Song等[10]首次采用数值模拟的方法研究了接触线存在磨损的接触网的舞动行为,结果表明,增大接触网拉力可有效抑制接触网舞动,随机风对接触网舞动影响较小.Avila-Sanchez等[11]通过风洞试验获得了铁路桥上的接触线的气动系数,并基于Den Hartog判据考察了磨损接触线在安装不同类型风挡时的稳定性.张友鹏等[12]研究了接触网正馈线考虑表面粗糙度时的舞动特性,结果显示,考虑表面粗糙度会使接触网正馈线的舞动幅值明显降低,其作用不可忽略,该结论可为接触网的建模与舞动抑制提供参考.当接触网覆冰时,接触线、承力索截面的气动特性将发生改变,在横风作用下容易发生舞动.班瑞平[13]对当时发生的两次罕见的接触网舞动现象进行了论述,分析了舞动现象发生的原因并探讨了预防措施.谢强等[14, 15]首先对接触网的缩比模型进行了风洞试验并指出,无覆冰时的接触线模型受到的扭矩极小,接触线模型舞动主要是由垂向升力的变化引起.随后又研究了保留凹槽的覆冰接触线的气动特性,结果表明,覆冰接触线上的凹槽对其气动特性有明显消极影响且覆冰厚度的增大会降低接触线的气动稳定性.Chen等[16]研究了覆冰接触网的垂向舞动行为,考察了结构阻尼、初始覆冰角及风速对覆冰接触网气动稳定性的影响.陈果[17]建立了覆冰接触网多向耦合模型,研究了考虑几何非线性的覆冰接触网的舞动行为,并强调只有几何非线性模型才能很好地描述结构在横风下的舞动行为.
本文以覆冰接触网为研究对象,考虑到接触网覆冰后其下仍可有受电弓通过,从而“重塑”覆冰接触线的截面形状,将覆冰接触线与覆冰承力索的截面设置成不同形状,考察了覆冰接触网的舞动特性,揭示了覆冰初始攻角、几何非线性及覆冰厚度对接触网稳定性的影响.
1 覆冰接触网气弹模型
1.1 接触网模型
覆冰接触网实物模型如图1(a)所示,将其简化为图1(b)所示的力学模型,其中吊弦在某时刻的运动状态如图1(c)所示,由于吊弦较细,忽略吊弦的覆冰影响.将覆冰接触线与承力索简化为两端简支的Euler-Bernoulli梁,将吊弦视为拉压刚度不一致的非线性弹簧,其压缩刚度为拉伸刚度的1/100[18],支撑杆以及定位臂则简化成线性弹簧,并作假设:(a) 覆冰接触线和承力索的截面在运动过程中不发生变形,即截面为刚性;(b) 覆冰接触线和承力索在发生变形后,其中性轴仍垂直于截面;(c) 覆冰接触线和承力索的截面沿接触网跨长方向不变且方向一致.
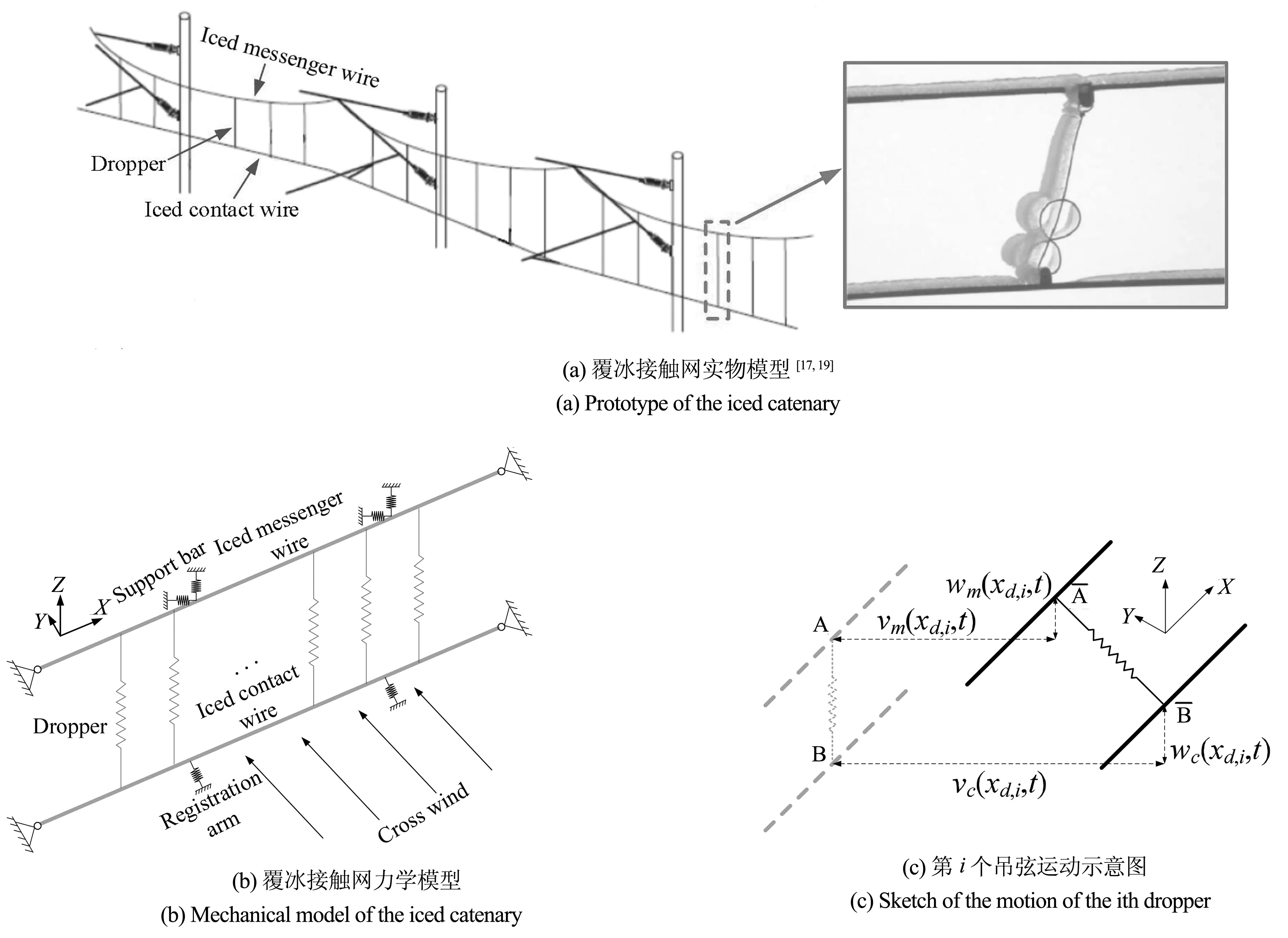
图1 覆冰接触网模型示意图Fig.1 Sketch of the mechanical model of the iced catenary
覆冰接触线考虑几何非线性的运动方程的详细推导可参见文献[20],受限于篇幅,这里直接给出其运动方程如方程(1)所示.考虑到实际接触线、承力索的轴向运动相比于垂向、横向运动小很多,为简化运动方程,此处忽略了轴向运动.有必要指出,方程(1)相比于文献[17]更多地考虑了覆冰接触线扭转的影响,若将这些与扭转相关的项剔除,方程(1)即可退化为文献[17]中覆冰接触线的运动方程.另外,本文中覆冰接触线和承力索的截面形状互不相同(见图2(b)和图2(c)),从而使得本文覆冰接触网上的气动力有别于文献[17]中的气动力.
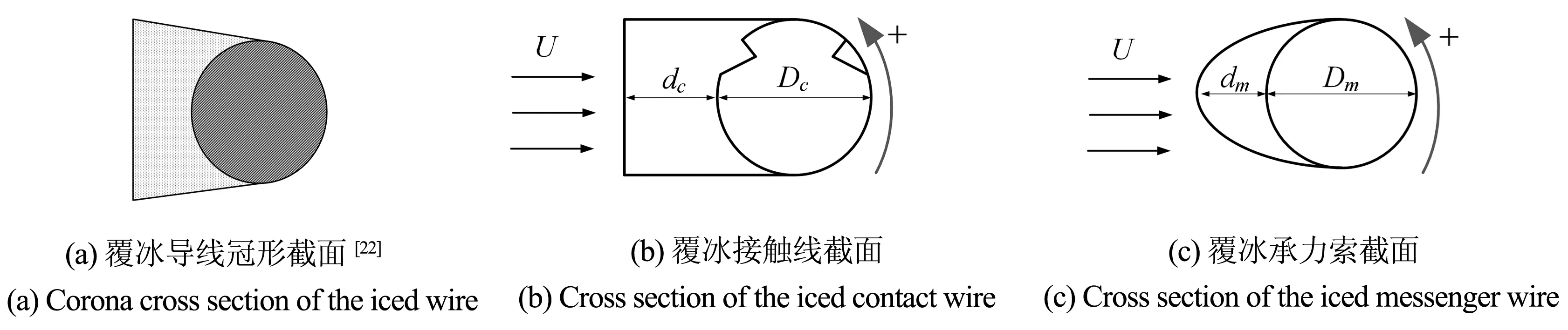
图2 截面形状及攻角定义Fig.2 Sketch of the cross-sectional shape and the definition of the attack angle
(1a)
(1b)
(1c)
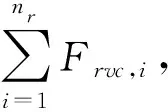
Fdwm,i=[-kd,i(wm-wc)-0.5kd,i/ld,i(vc-
Fdvm,i=[-kd,i/ld,i(wcvc-wmvc-wcvm+
Fdwc,i=-Fdwm,i,Fdvc,i=-Fdvm,i
(2a-c)
其中,kd,i、ld,i、xd,i为第i个吊弦的拉伸刚度、原长及在整个接触网中的位置.
1.2 气动力模型
基本假设:(a) 气动力为准定常气动力;(b) 接触线与承力索的气动力互不影响.新月形与冠形是覆冰输电线常见的两种截面形状[22],如图2(a, c)所示.接触网与输电线具有相似结构,且在实际运行中,覆冰后的接触线仍可能有受电弓往复通过,其截面形状可能会被“重塑”.因此,覆冰接触线与承力索的截面分别设置成冠形与新月形.另外,图2(a)中冠形截面上下边与水平面的夹角在实际中会随环境变化而发生改变,为消除这种变化的影响,同时使截面更具一般性及方便后续研究,取该夹角为0,得到图2(b)所示形状.另定义覆冰接触线、承力索的冰形系数λc和λm(见式(3))及截面攻角正方向(见图2(b)和图2(c)箭头所示).当攻角为180°时,在实际中则意味着风向反向.
(3a, b)
这里,Dc、Dm为未覆冰接触线、承力索的直径,dc、dm为接触线、承力索的覆冰厚度.
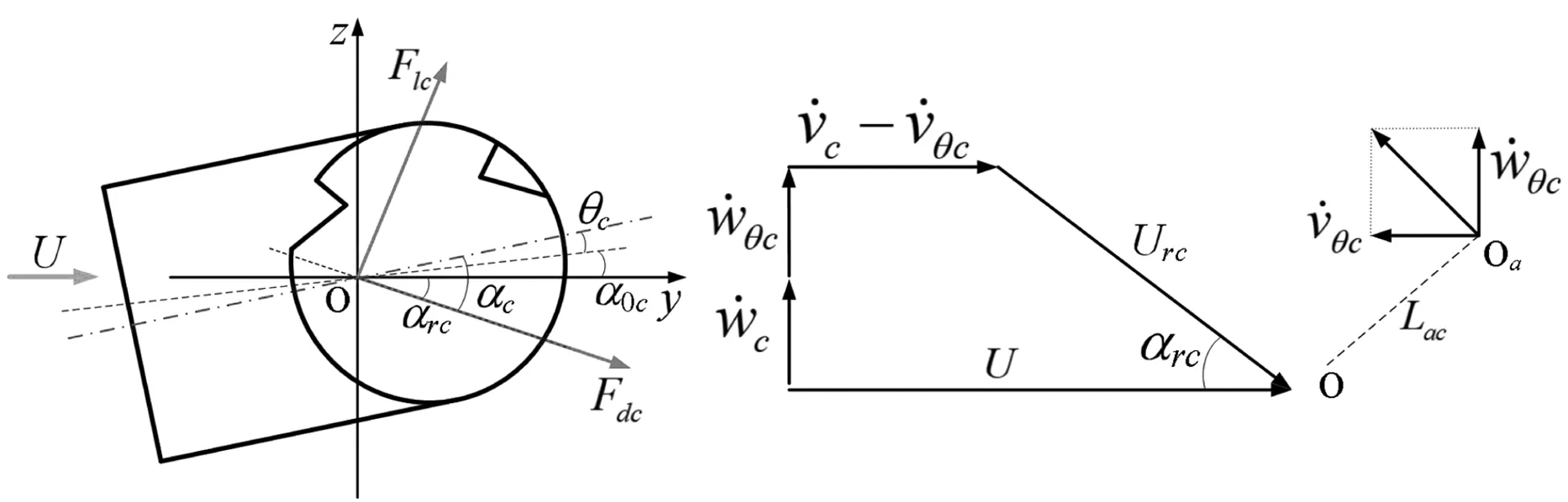
图3 覆冰接触线气动力示意图Fig.3 Sketch of the aerodynamic force of the iced contact wire
(4a)
(4b)
(5a)
(5b)
αc=α0c+θc-αrc
(6)
于是,覆冰接触线单位长度的气动升力Flc、气动阻力Fdc、气动力矩Fmc为
(7)
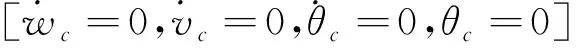
(8)
此处覆冰接触网运动方程的推导建立在系统的平衡位置上,因此式(8)中忽略了常数项.由于项数
较多且表达式相对复杂,此处仅给出线性项的系数表达式,F1c、F2c、F3c为非线性项,见附录2,其中的气动系数通过FLUENT软件获得,与文献[22]的结果对比,验证了气动系数计算的正确性,同时式(8)的收敛性见附录3.作用于覆冰承力索上单位长度的气动力,与式(8)具有相似表达式,此处不再赘述.文献[5]建立了覆冰输电线三自由度模型的气动力模型并将其Taylor展开到三阶,现忽略文献气动力表达式中横风脉动相关项,所得结果可验证本文气动力模型的正确性.
接触网参数如表1和表2所示.冰的密度为900 kg/m3,覆冰接触网采用Galerkin方法离散,垂向弯曲、横向弯曲、扭转向模态截断数分别为10、10和1,此处的模态是整个10跨接触网的模态.考虑到覆冰接触网构型相对复杂,不易获取其解析模态,故采用有限元方法获取其数值模态,并以此作为覆冰接触网采用Galerkin方法离散时的基函数.此处在计算覆冰接触网数值模态时,覆冰接触网两端为简支,限于篇幅,具体计算方法及振型可参见文献[17].时间积分方案为定步长Runge-Kutta方法,时间步长5 ms.在进行响应计算前,首先对非线性覆冰接触网的派生系统进行稳定性分析,获得该派生系统的失稳边界,此处的稳定性判定法则可参考文献[23].之后,选取典型参数,计算非线性覆冰接触网的响应并分析其特性,风速考察范围为0~20 m/s.本文仅讨论α0m=α0c情形并令α0m=α0c=α0,这里α0m为覆冰承力索的初始攻角.本文响应计算时的初始值设定为0,但在展示时程响应时仅截取稳态响应中的一段,并将时间设置为从0开始.

表1 接触网参数1Table 1 Parameters of the catenary-part one
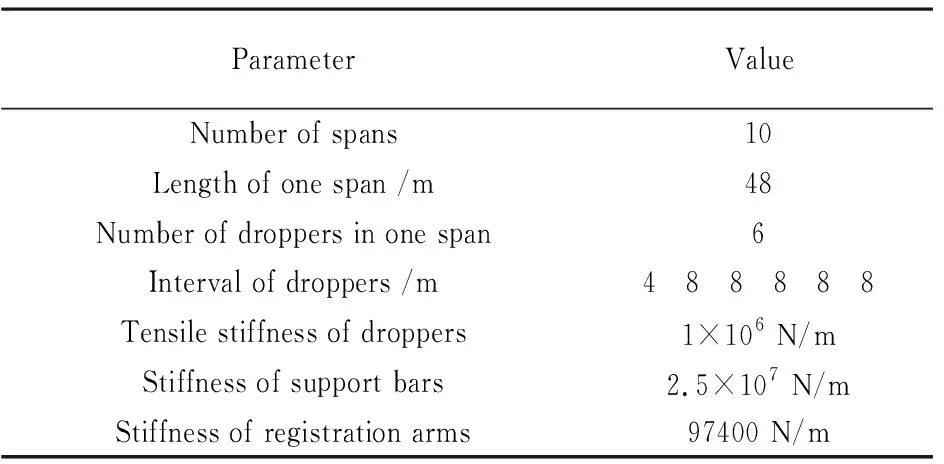
表2 接触网参数2Table 2 Parameters of the catenary-part two
1.3 接触网模型验证
采用文献[24]中的接触网参数及气动系数.为体现接触网的几何非线性,模型验证时取U=30 m/s,风攻角为10°,不考虑覆冰.图4给出了接触线中跨中点位移的频谱,从中可以看出,对于接触线垂向位移,主频为1.14 Hz,对于横向位移,主频为1.58 Hz,这与文献[24]中的结果较为接近:垂向位移主频1.16 Hz以及横向位移主频1.59 Hz.此外,也能够从图中观察到第一个较低频率的脉动风主频,与文献[24]中的相应结果一致.这表明,本文建立的接触网模型具有较高的可信度.
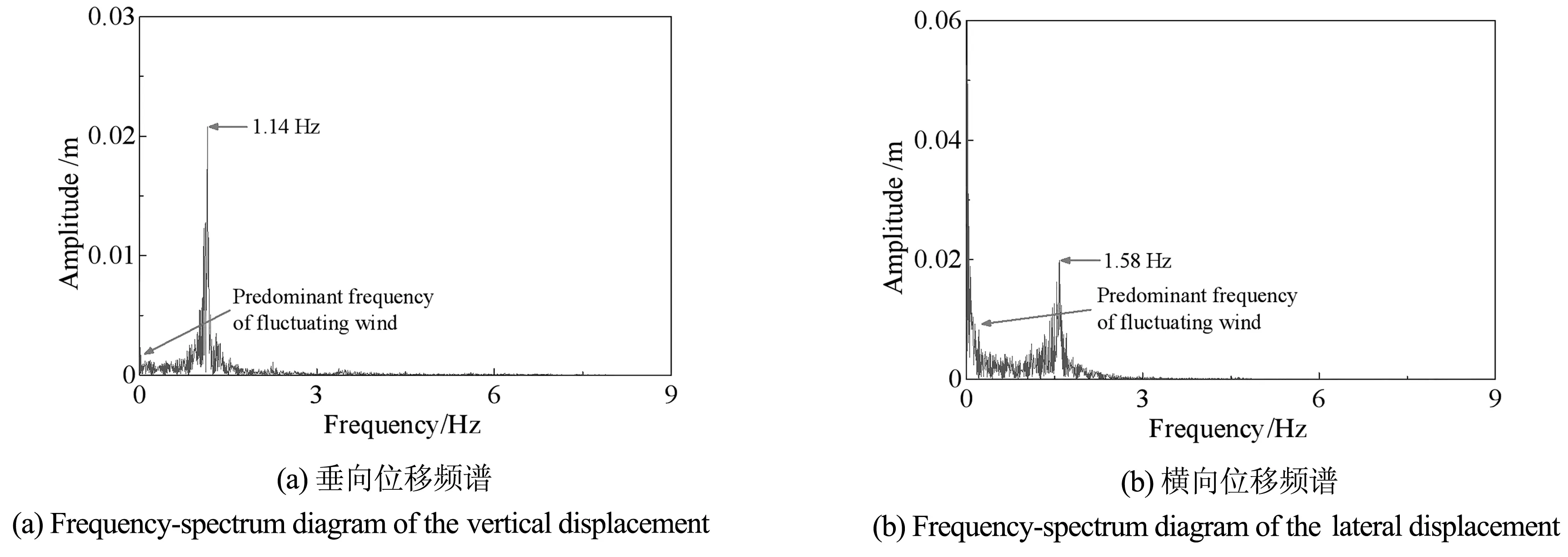
图4 接触线中跨频谱Fig.4 Frequency-spectrum diagram of the mid-span contact wire
1.4 舞动特性
在本小节中,取λc=λm=1.6.当α0=9.8°,U=15 m/s时,覆冰接触网发生舞动,其第5跨中点位移时程与频谱如图5所示.图(a)显示,覆冰承力索垂向运动时程几乎与覆冰接触线重合,两者均包含两个频率:1.32 Hz与1.56 Hz(见图5(d)).由于对应于1.56 Hz的幅值较小,图5(a)中的时程为近似单频简谐.覆冰接触线的横向运动则表现出明显的拍振现象(见图5(b)),其主频包含能量最大的1.32 Hz及其余两个频率1.56 Hz和2.64 Hz(见图5(e)).覆冰承力索的横向运动为近似单频简谐振动,包含1.32 Hz和1.56 Hz两个频率.至于承力索横向运动,其为近似单频简谐振动,包含能量较大的主频1.32 Hz以及能量较小的1.56 Hz.覆冰接触线扭转位移的最大主频为1.32 Hz,其近似为一单频简谐振动(见图5(f)),而承力索的扭转运动中则另外存在明显的2.64 Hz倍频.在本文中,扭转模态仅取1阶,然而在扭转运动中存在两个频率,其主要由覆冰接触网各个方向的运动耦合导致.总体来看,覆冰接触网的运动主要表现在垂向,横向运动较小,且为低频振动.
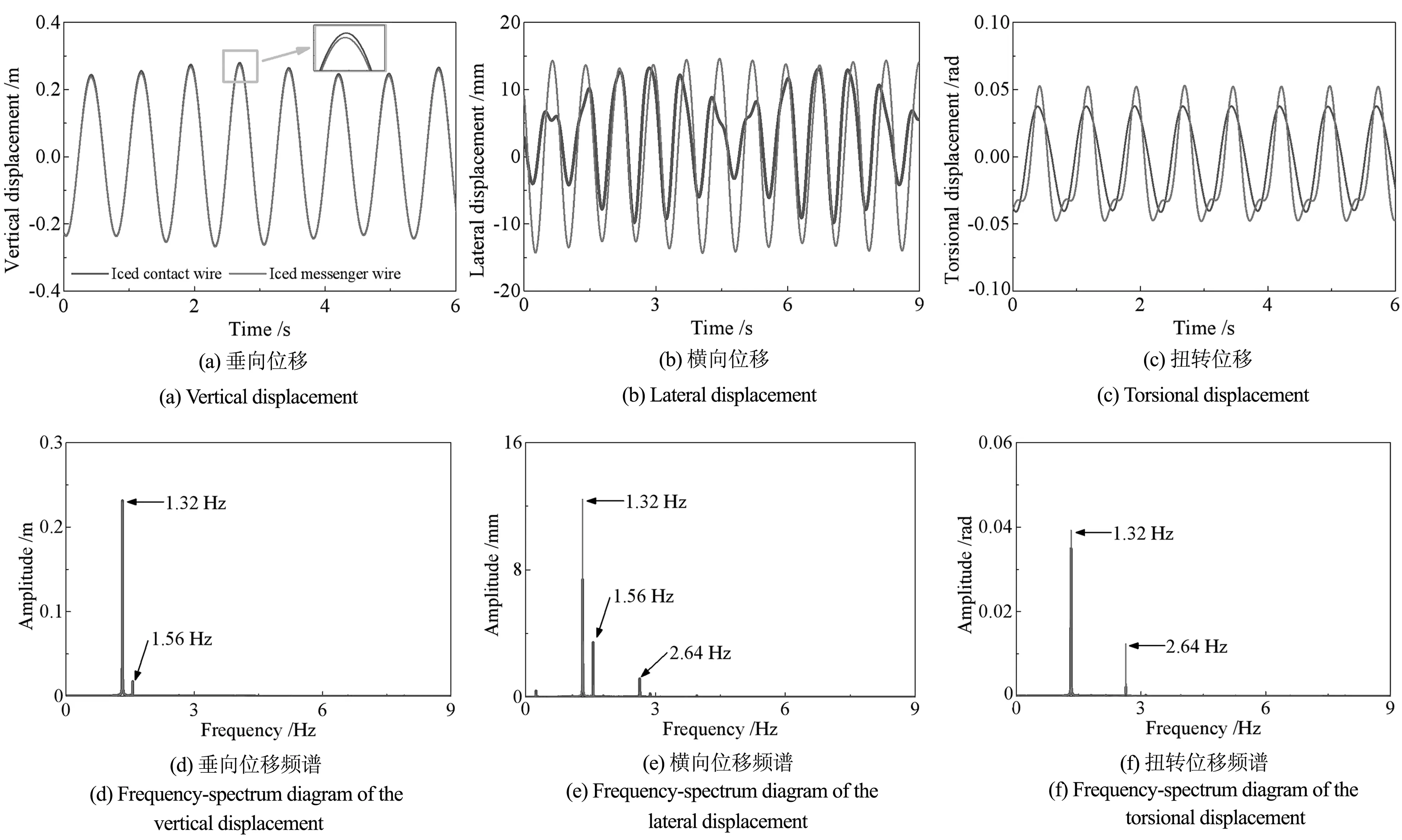
图5 α0=9.8°,U=15 m/s时第5跨覆冰接触线中点的位移时程与频谱Fig.5 Time history of the displacement and frequency-spectrum diagram of the 5th-span iced contact wire atα0=9.8°and U=15 m/s
覆冰接触网每跨的主频可能不相同.如图6所示,第1跨覆冰接触线垂向运动能量最大的主频为1.56 Hz,而第5跨为1.32 Hz(见图5(d)),这主要由接触网的结构特性导致.在接触网中,承力索处的支撑杆和接触线处定位臂的刚度(见表1)远大于接触网线索的弯曲或扭转刚度,其对支撑杆或定位臂两侧的线索运动起到了一定的“隔离”作用,而第1跨包含了整个接触网的端部约束,从而使得第1跨的刚度大于其他跨,因而主导频率稍大.
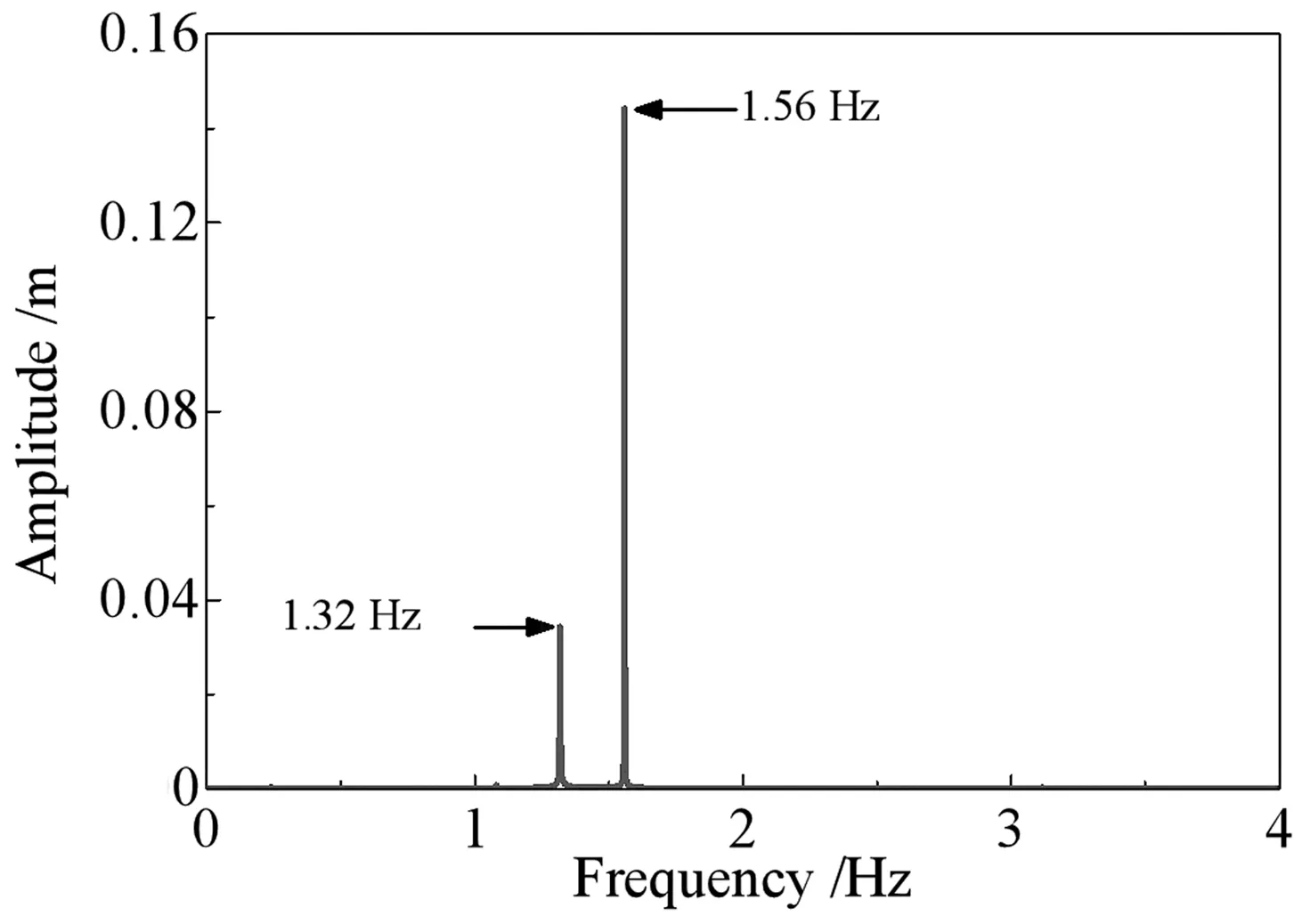
图6 第1跨覆冰接触线垂向位移频谱Fig.6 Frequency-spectrum diagram of the vertical displacement of the 1st-span iced contact wire
通过频谱分析可获得主频所对应的幅值.覆冰接触网垂向运动中,仅存在两个频率,由拍振的特性可知,这两个频率幅值的和与差即为拍振的最大与最小振幅.图7给出了最大振幅与最小振幅的比值,该比值越大,拍振现象越明显.相反,越接近于1则越弱.从图中可以看出,覆冰接触线每跨垂向运动的拍的强度可能不尽相同,但关于接触网中点对称.当α0=9.8°时,接触线第2跨和第9跨的拍振现象最明显,而第1、5、6和10跨则为近似单频简谐振动,这也可以从图5(a)得到验证.当α0=164°时,第1、5、6和10跨的接触线拍振现象最明显,而第3和8跨则为近似单频简谐振动.另外,接触网每跨的最大垂向、横向位移也可能不一致,如图8所示.当α0=9.8°时,最大垂向位移发生在第4跨和第7跨内,而当α0=164°,最大垂向位移则发生在第1、5、6和10跨内.由此可见,考察覆冰接触网的振动形式、统计最大舞动位移时,仅观察一跨可能会引起一定的误差,应至少观察接触网所有跨数的一半.此外,当α0=9.8°时,第5跨和第6跨承力索接触线的最大垂向位移有不可忽略的差异,这表明吊弦可能存在较多松弛,并且无论攻角如何,横向位移总是比垂向位移小一个数量级.图9给出了覆冰接触线第1跨和第5跨中点的运动轨迹,从图中可以看出,该两跨的运动轨迹存在明显的差异,而第2、3、4跨中点的运动轨迹和该两跨的也互不相同(此处未画出),其原因如上所述,覆冰接触网各跨的拍振强度及最大位移互不相同.
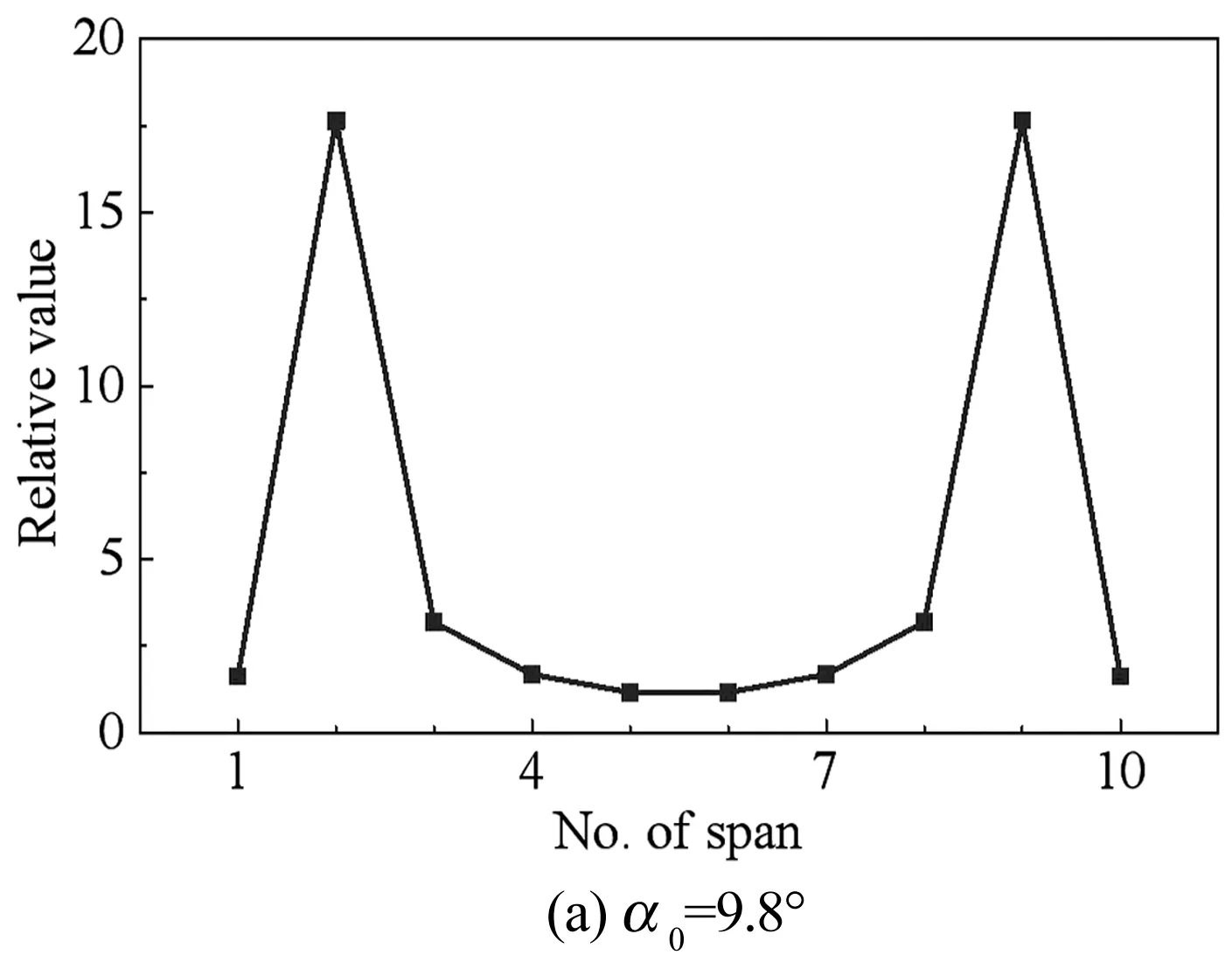
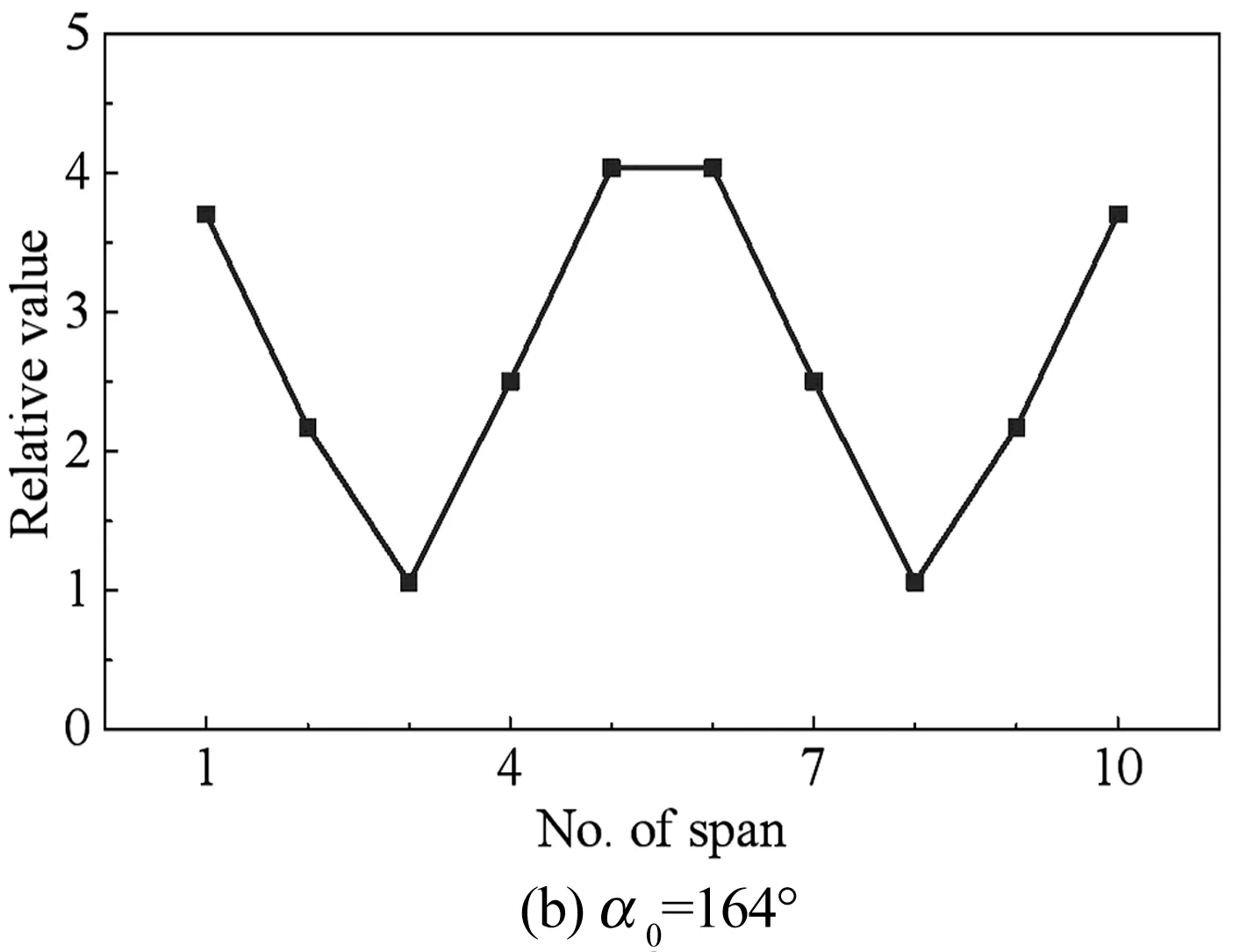
图7 覆冰接触线垂向拍振运动中最大、最小振幅比率Fig.7 Ratio between the maximum and the minimum amplitudes of the vertical beat vibration of the iced contact wire
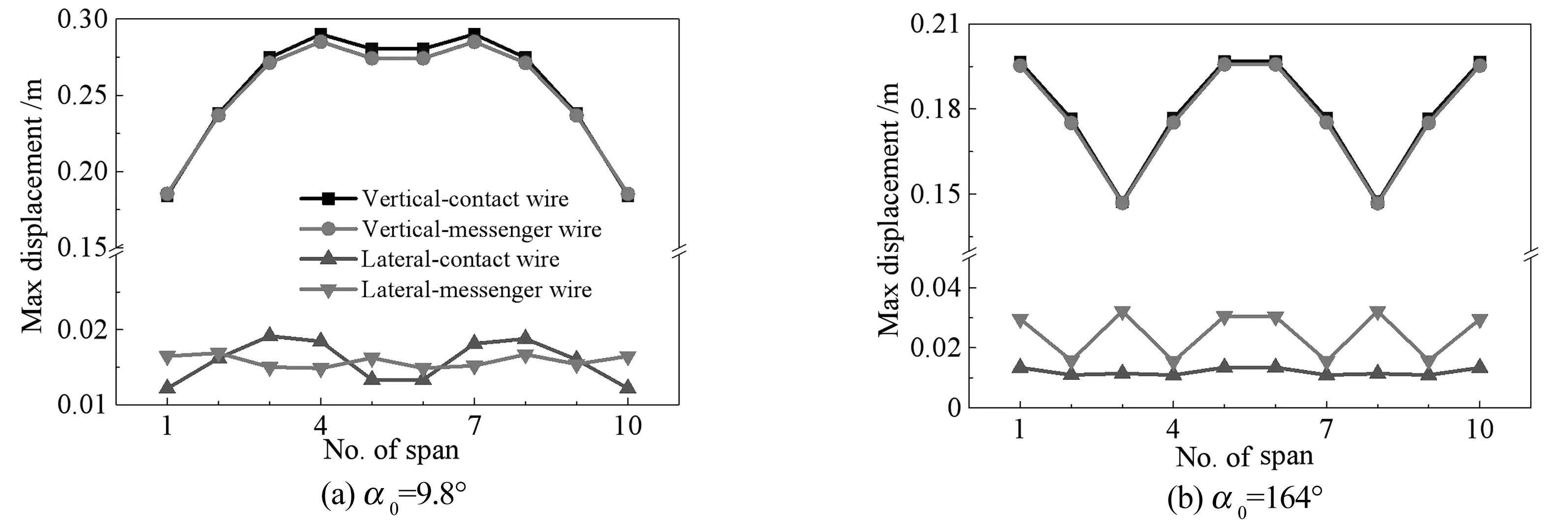
图8 覆冰接触网各跨最大位移Fig.8 The maximum displacements of each span of the iced catenary

图9 覆冰接触线轨迹Fig.9 Track of the iced contact wire
通过响应计算,当风速逐渐增大时,覆冰接触网将由逐渐收敛到平衡位置的运动变为极限环振动,将该转折点称为非线性临界风速.为区分,将由稳定性分析获得的临界风速称为线性临界风速.从图10可以看出,对于α0=9.8°和α0=164°的情况,非线性临界风速均为5 m/s.在临界风速之后,最大垂向位移随风速的增大呈现近似线性增加的趋势,而即使风速达到了20 m/s,横向和扭转位移依旧较小.在实际中,覆冰总是在线索的迎风侧,而α0=164°则意味着风向几乎反向,在实际中遇到的可能性相对较小.因此,α0=9.8°比α0=164°更可能遇到,并且响应更大,接触网也更危险.现考察在小攻角处覆冰接触网几何非线性的影响.图11给出了在α0∈[0°,20°]时不同风速下通过稳定性分析与响应计算所得的失稳区域(图中阴影部分),从中可以看出,通过响应计算得到的系统失稳区域小于由稳定性分析所得的区域,显示出系统的几何非线性特征将使系统变得稳定.
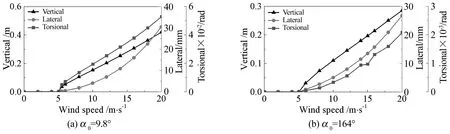
图10 不同风速下覆冰接触线的最大位移Fig.10 The maximum displacements of the iced contact wire as a function of the wind speed
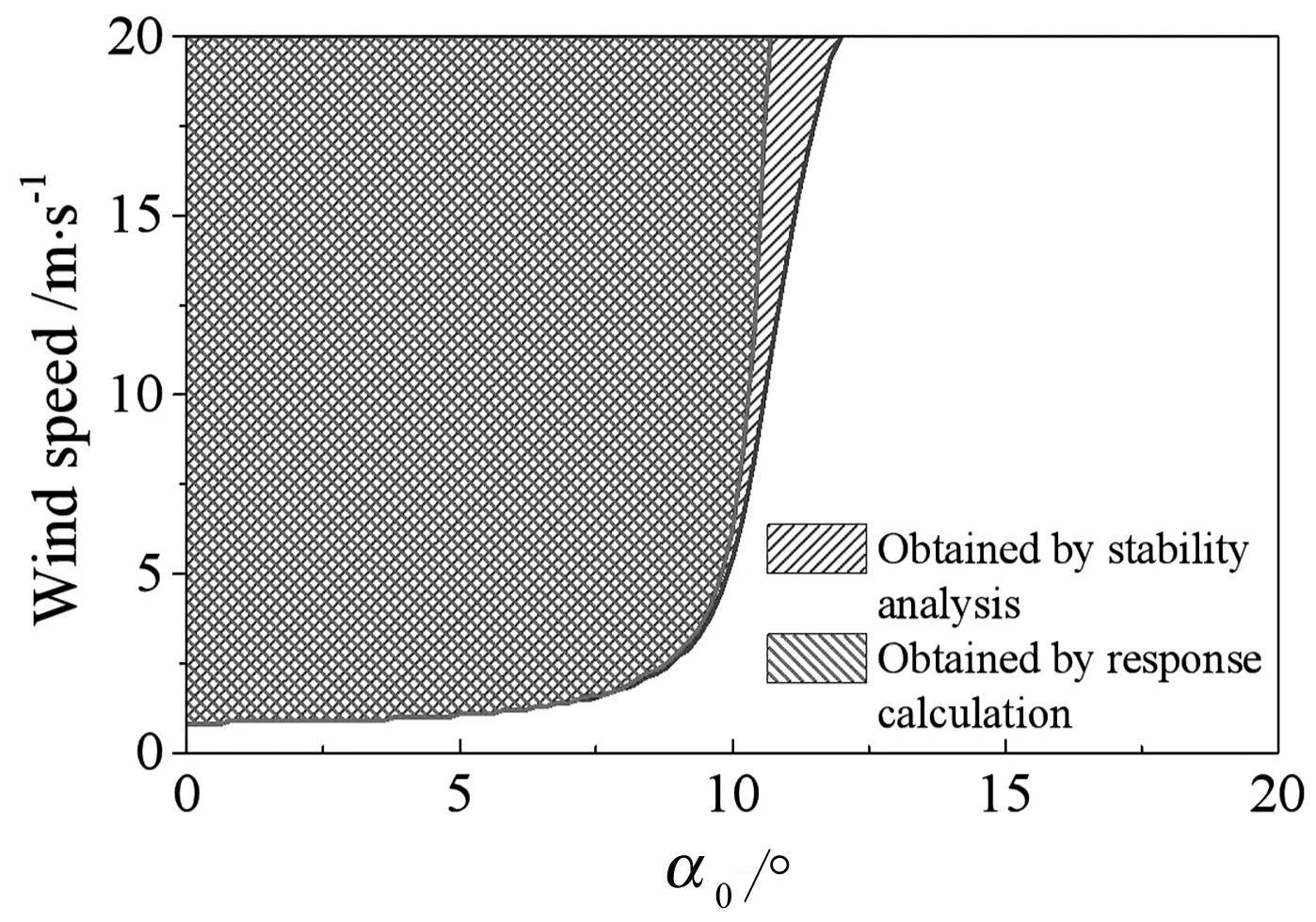
图11 覆冰接触网的不稳定区域Fig.11 The unstable area of the iced catenary
1.5 覆冰厚度的影响
考察在实际中更可能遇到的小攻角处覆冰厚度对覆冰接触网非线性临界风速的影响.取α0=9.8°,非线性临界风速随冰形系数的变化规律如图12所示.当λm=λc时,随着冰形系数的增大,非线性临界风速单调增大,但总是落在[4 m/s,6 m/s]的风速区间内.取λc=1.6,随着λm的增大,非线性临界风速单调减小.特别地,当λm=1.2时,非线性临界风速已超过风速考察范围(此处未画出).取λm=1.6,与λc=1.6时的情形不同,此时尽管非线性临界风速随λc的增大而单调增大,然而即使λc=1.8,非线性临界风速也未超过9 m/s.因此,承力索冰形系数的变化对接触网稳定性的影响比接触线更大,其使覆冰接触网的非线性临界风速变化剧烈.在实际中,为减小风的影响,在大风区的接触网可能会设置风挡.通常,风挡的高度接近于承力索高度.这使承力索的覆冰厚度相比于接触线更容易发生改变.从图12可以看出,承力索覆冰越厚,非线性临界风速越小,从而使接触网越容易发生失稳.因此,尽管风挡可以减小接触网的风致振动,但其在某些情况下可能使得接触网更容易发生舞动,在设计安装风挡时应格外注意.
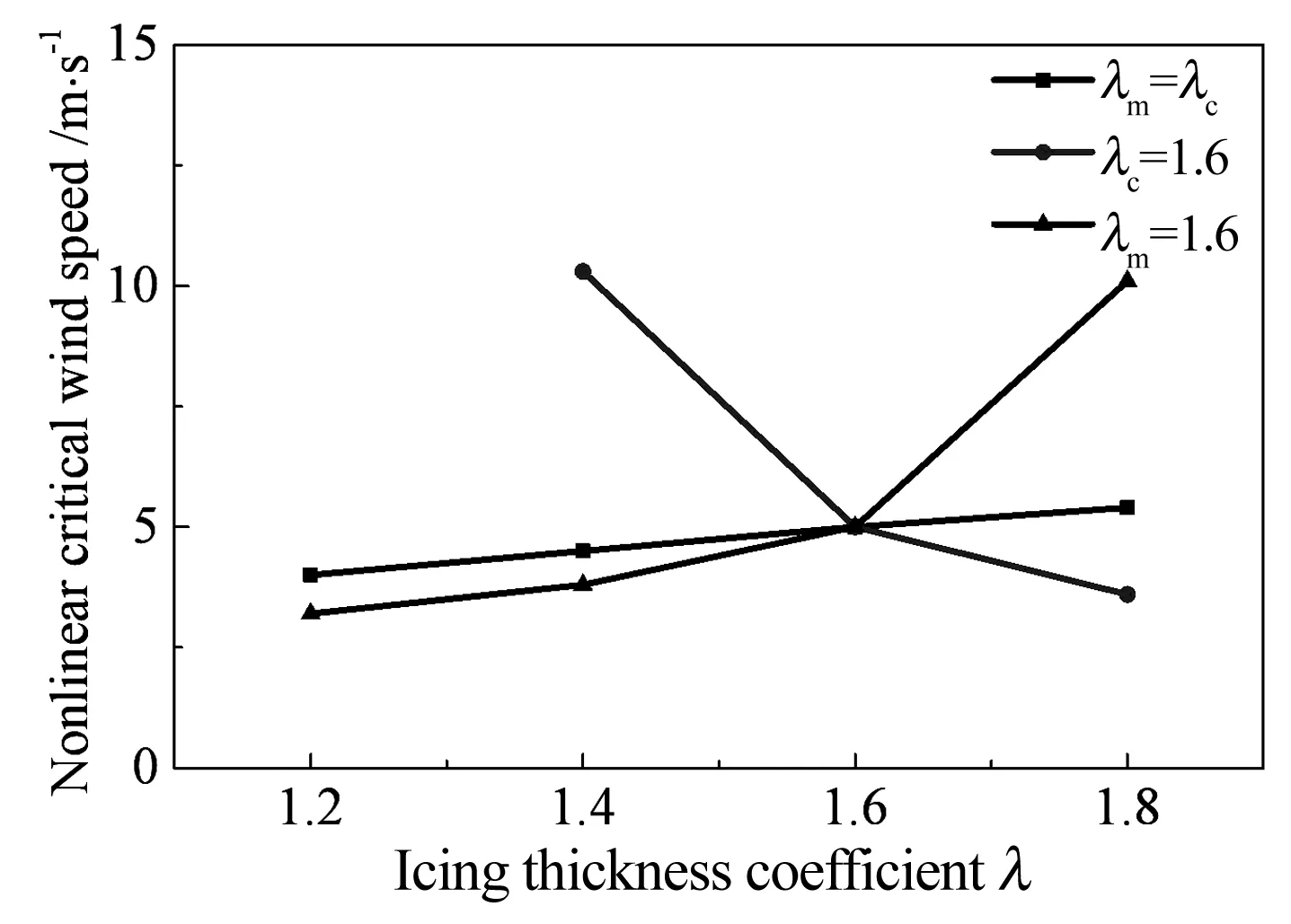
图12 α0=9.8°时覆冰接触网非线性临界风速随冰形系数的变化Fig.12 The nonlinear critical wind speed of the iced catenary as a function of the icing thickness coefficient atα0=9.8°

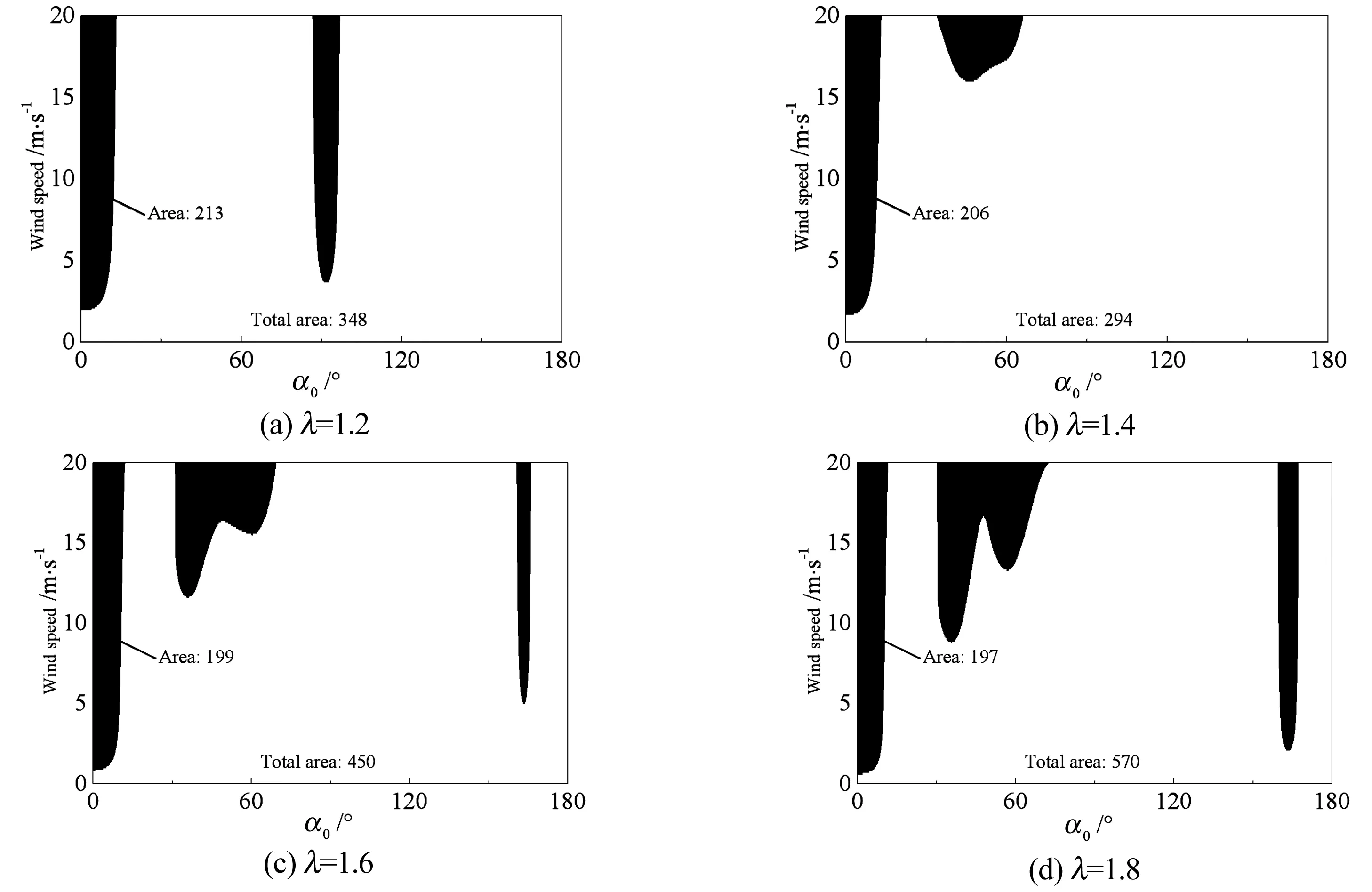
图13 α0m=α0c时覆冰接触网的不稳定区域Fig.13 The unstable area of the iced catenary whenα0m=α0c
2 结论
本文以覆冰接触网为研究对象,考虑了受电弓反复通过对覆冰接触线截面形状的“重塑”作用,将覆冰接触线与覆冰承力索设置成不同的截面形状,研究了覆冰接触网的舞动特性及覆冰厚度的影响,得到如下主要结论:
(1)覆冰接触网的舞动主要发生在垂向,且为低频振动,各跨的主频、拍振强弱及轨迹可能互不相同,最大垂向、横向位移可能不在中间跨,但关于接触网中点对称,在考察覆冰接触网振动形式及最大、最小舞动位移时建议至少取一半的接触网跨数进行观察与统计.
(2)实际中的覆冰接触网更可能在小攻角下发生舞动,舞动时的最大位移比大攻角时的相应值更大,对接触网的安全更不利;覆冰接触网的几何非线性将使得系统更稳定.
(3)承力索覆冰厚度的变化对覆冰接触网稳定性的影响比接触线更大,其使得覆冰接触网的非线性临界风速变化剧烈,建议在设计安装接触网风挡时加以考虑;覆冰厚度越大,覆冰接触网的线性临界风速越小,但在小攻角处存在基本的失稳区域,其不随覆冰厚度的变化而发生明显的变化.
