跨接管缆长度精确计算与优化
2022-07-19杨勇董海防朱刚余骁周梁
杨勇,董海防,朱刚,余骁,周梁
(武汉第二船舶设计研究所,武汉 430064)
当海洋核动力平台通过单点系泊系统实现驻泊时,其生产的电力能源、热能,以及淡水资源需先通过跨接电缆或跨接软管传输到单点系泊管汇平台,进而通过旋转接头传输至海底电缆或管道并最终送达用户。
关于跨接管缆及悬索的计算方法,已有研究都是基于悬链线理论或者是改进的悬链线理论进行的,相关的工程应用中,悬链线理论都是用作精度较高的计算分析工具,而关于悬链线算例的规律分析和跨接管缆长度优化设计方面尚鲜见报道。考虑基于悬链线理论对跨接管缆类工程应用进行算例分析,总结计算结果的规律,期望为跨接软管、电缆和索道的安装计算等工程实践提供更加直观便捷的设计参考。
1 跨接管缆计算模型
1.1 模型假设
考虑到跨接管缆的物理特性,为简化分析,对跨接管缆计算模型采用以下假设:①缆索、软管是理想柔性的,既不能承受压力也不能承受弯曲,其截面尺寸和长度相比十分微小,因此忽略截面的抗弯刚度;②缆索、软管材料符合胡克定律,在正常受力情况下发生小弹性变形且应力和应变符合线性关系;③缆索、软管的自重荷载集度(即单位长度重量)为定值,但在变形前后不同,通过迭代计算来求解截面面积和自重载荷集度变化的影响。
1.2 跨接管缆悬链线模型建立
悬挂于、两点之间的跨接管缆呈悬链线形状,见图1。在自重和、两点拉力作用下保持平衡、静止状态。取较低悬挂点为坐标原点,建立平面直角坐标系。图1中:和分别为跨接2点的跨距和高差;为跨接2点距离;为跨接管缆长度,m;为跨接管缆自重载荷集度,N/m;和分别为、两点对管缆的拉力,N,拉力方向与管缆在对应悬挂点的切线方向一致;和分别表示、两点拉力方向与轴所夹锐角,rad。和正负号的定义为:轴(即水平方向)旋转该角度后与该切线平行,若逆时针旋转即为正,顺时针则为负,图1中为负值,为正值。

图1 跨接管缆在静止状态下悬链形状
采用悬链线理论对跨接缆索或软管的跨接进行静力学分析,推导出图1所示悬链线方程如下。

(1)

由式(1)求导得到该悬链线任意点切线斜率为

(2)
因此,跨接管缆两端连接点处的斜率及相应角度为

(3)

(4)
根据式(2)推导出跨接管缆上任意点的张力为

(5)
距离跨接管缆最低点越远,其张力越大,最大张力值记为;最低点处张力与水平拉力相等。跨接管缆两端连接点处的拉力为
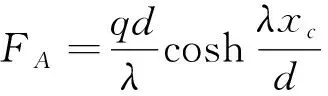
(6)
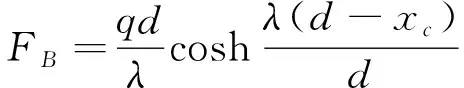
(7)
跨接管缆上任意点的曲率半径为

(8)
显然,在跨接管缆线形的最低点处曲率半径最小,可表达如下。

(9)
依据式(1)计算曲线弧长,可推导出跨接管缆有应力长度为
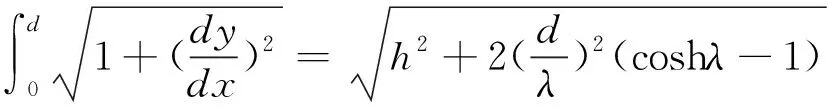
(10)
进而由胡克定律可得跨接管缆在自身重力和悬挂点拉力的作用下产生的弹性伸长量Δ。
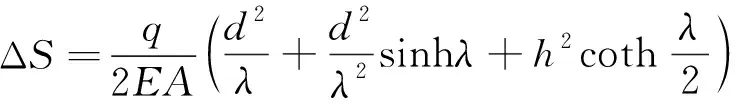
(11)
式中:为跨接管缆的弹性模量;为跨接管缆的有效截面积。
那么,跨接管缆悬挂前无应力状态长度为


(12)
式中:为跨接管缆的弹性模量;为跨接管缆的有效截面积。有应力自重载荷集度和无应力自重载荷集度的关系为
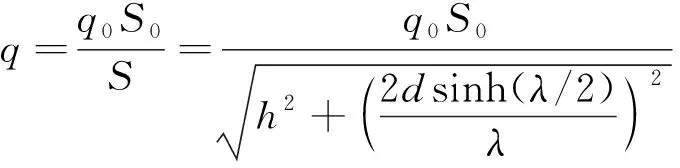
(13)
2 数值计算
已知跨接两点的跨距、高差和待悬挂管缆的物理属性(包括无应力自重载荷集度、弹性模量和有效截面积),此外还需给出跨接管缆无应力长度(也可以是有应力长度),或者跨接管缆某一点拉力状态(可以是、、、或等)。可根据这些条件求得跨接管缆的形状、有应力长度、最小曲率半径、两端锚固拉力和角度等。
基于以上建立的跨接管缆悬链线模型,运用迭代计算、逐步逼近的方法求解,具体步骤如下。
2.1 已知跨接管缆无应力长度S0
1)输入计算工况的跨距、高差、管缆无应力长度、无应力自重载荷集度、有效截面积和弹性模量。
2)设定管缆有应力长度和有应力自重载荷集度的初始值和,=、=、Δ=0。
3)将各变量值带入式(10)中,解方程可解得无荷水平拉力系数,将代入式(11)求得弹性伸长量Δ,则有应力长度=+Δ,而有应力自重载荷集度=。
4)重复步骤3),不断根据计算结果对和的值进行修正,直至=|Δ+1-Δ|≤或=|Δ+1-Δ|≤时停止迭代,和分别为事先设定的绝对和相对精度要求,一般绝对精度可设置为毫米量级,而相对精度取值范围可选0.000 1~0.000 001。
5)将求解所得值代入式(3)~(9)中,求出所关注的各个变量值。
2.2 已知跨接管缆某一点拉力(H)
1)输入计算工况的跨距、高差、无应力自重载荷集度、有效截面积、弹性模量和跨接管缆拉力水平分量。
2)设定管缆有应力自重载荷集度的初始值=、Δ=0。
3)将各变量值带入=中,解方程可解得无荷水平拉力系数,将分别代入式(10)和(11)中求得有应力长度和弹性伸长量,则有应力自重载荷集度=(-Δ)。
4)重复步骤3),不断根据计算结果对和的值进行修正,直至=|Δ+1-Δ|≤或=|Δ+1-Δ|≤时停止迭代。
5)将求解所得值代入式(3)~(9)中,求解所关注的各变量值。
3 算例结果分析
3.1 量纲一的量化
为了能够获取更普遍的规律和更通用的结论,对模型变量进行量纲一的量化处理。量纲一的量化后的拉力变量将以长度为跨距的管缆重量为计量单位,长度变量以跨距为计量单位。

(14)
3.2 管缆长度对跨接管缆静力状态的影响
对不同高差的跨接应用进行大量算例计算,得到各个跨接工况下跨接管缆总长不同时跨接管缆的最大拉力云图、最小曲率半径云图,较低端部锚固角度云图和较高端部锚固角度云图。由于跨接管缆所用的材料、形状尺寸都不同,难以获得适用于所有材质和形状的跨接管缆的统一计算云图和规律。因此,云图算例计算结果都是以有应力状态的管缆长度来表征,不讨论悬挂前管缆长度和自重载荷集度。
不同跨接工况下跨接缆索最大拉力见图2。

图2 不同跨接工况下跨接管缆最大拉力云图
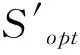
在不同跨接工况下跨接管缆最优长度见图3。

图3 不同跨接工况下跨接管缆最优长度

′=-0135 4′+0558 9′-
0008 832′+1258
(15)
从图3可知:随着跨接2点高差的增大,最优管缆长度也不断增大,且增长的速度渐渐加快直至近乎趋于一个定值、呈线性增长的趋势。

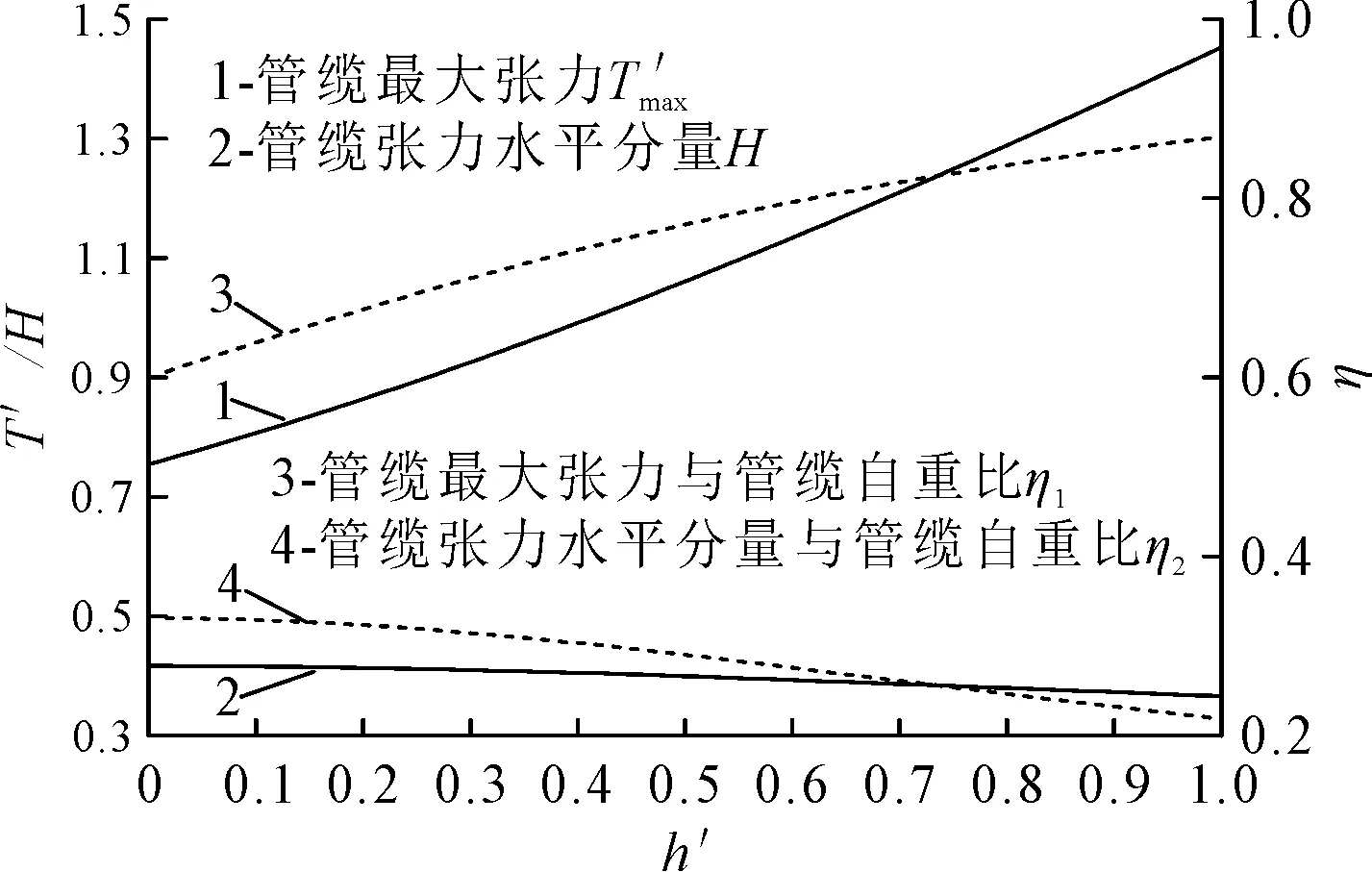
图4 不同跨接工况管缆总长最优时各变量值

在不同跨接工况下,当跨接管缆总长最优时跨接管缆线形最低点与较低悬挂端(即图1中点)的高度差Δ见图5。负值表示线形最低点低于点。
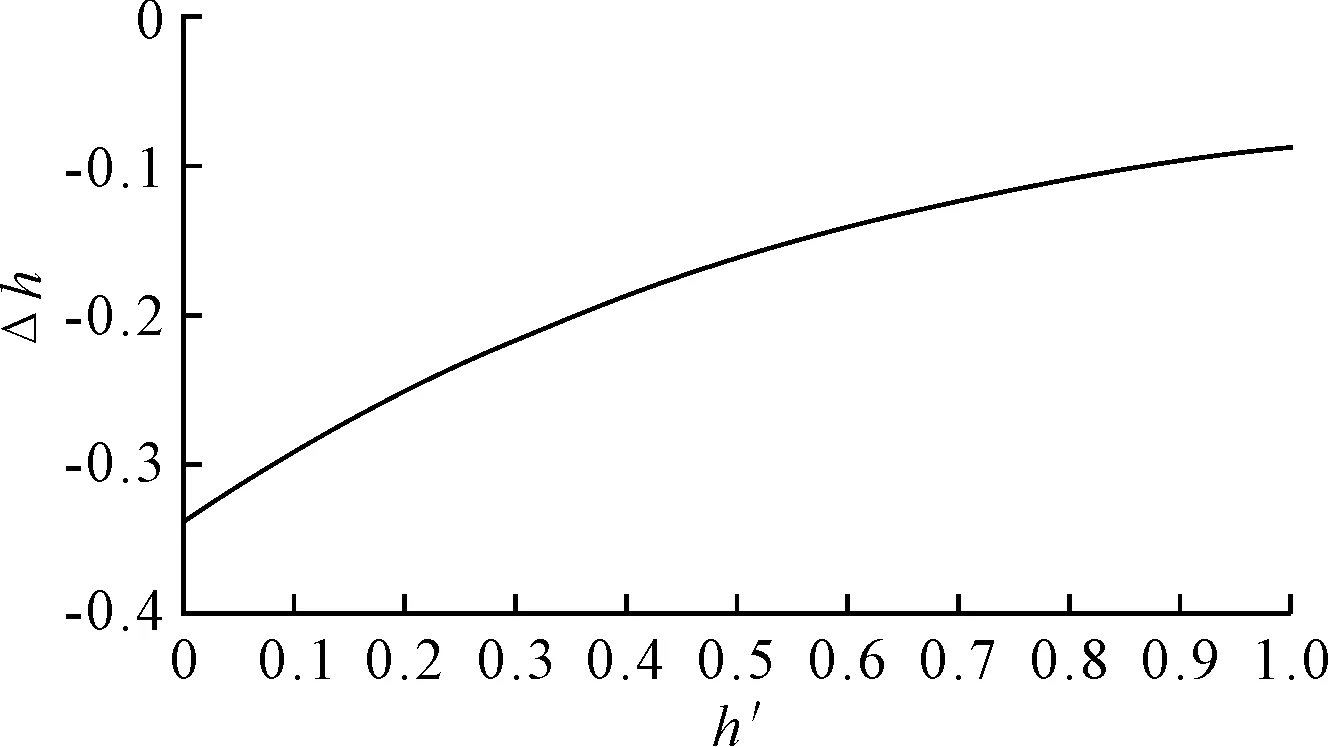
图5 不同跨接工况下管缆总长最优时跨接管缆最低点与较低悬挂端高度差
从图5可知,随着跨接2点高差′的增大,高度差Δ不断减小。在补给船和被补给船之间液货传输作业中,可以参看图5进行参数设置,以避免液货横向传输软管下部落入水中。
不同跨接工况下跨接管缆最小曲率半径云图见图6。

图6 不同跨接工况下跨接管缆最小曲率半径云图
在所有跨接工况下,最小曲率半径都是随着跨接管缆总长度的增大而不断减小。而在管缆总长最优时,不同跨接工况下跨接管缆的最小曲率半径见图7。
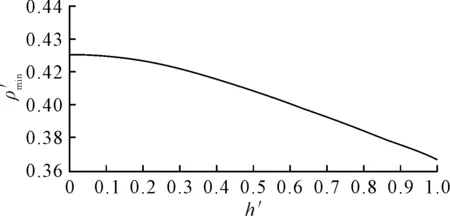
图7 不同跨接工况下管缆总长最优时最小曲率半径
随着跨接2点高差的增大,最小曲率半径不断减小,且减小的速度渐渐增大。
对于跨接缆索、软管的工程应用中,需要在跨接两端设置跨接管缆的锚固弯头,为实现合理安装、不致迫使跨接管缆发生额外受迫变形,需要准确获取两端锚固角度和。不同跨接工况下跨接管缆两端锚固角度见图8。
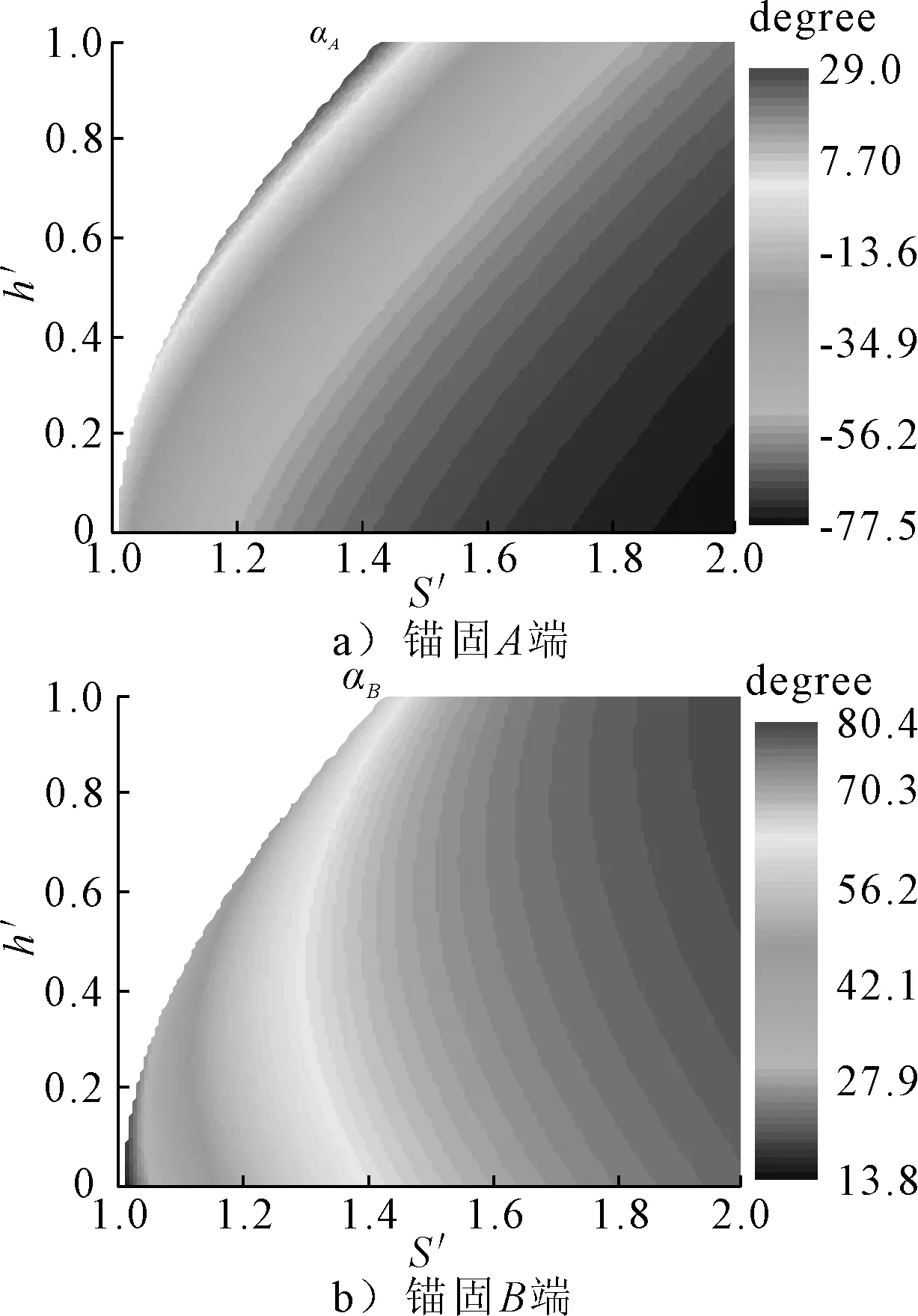
图8 不同跨接工况下跨接管缆两端锚固角度云图
从图8可知,高差一定时,随着管缆长度的增大,逐渐增大,而逐渐减小。在高差大于025且缆索长度较小时,出现正值,此时较低跨接端将是整个跨接管缆的线形最低处、曲率半径最小处和拉力最小处;而较高跨接端所有跨接工况下都是整个跨接管缆的线形最高处、曲率半径最大处和拉力最大处。
在管缆总长最优时,不同跨接工况下跨接管缆的最小曲率半径见图9。
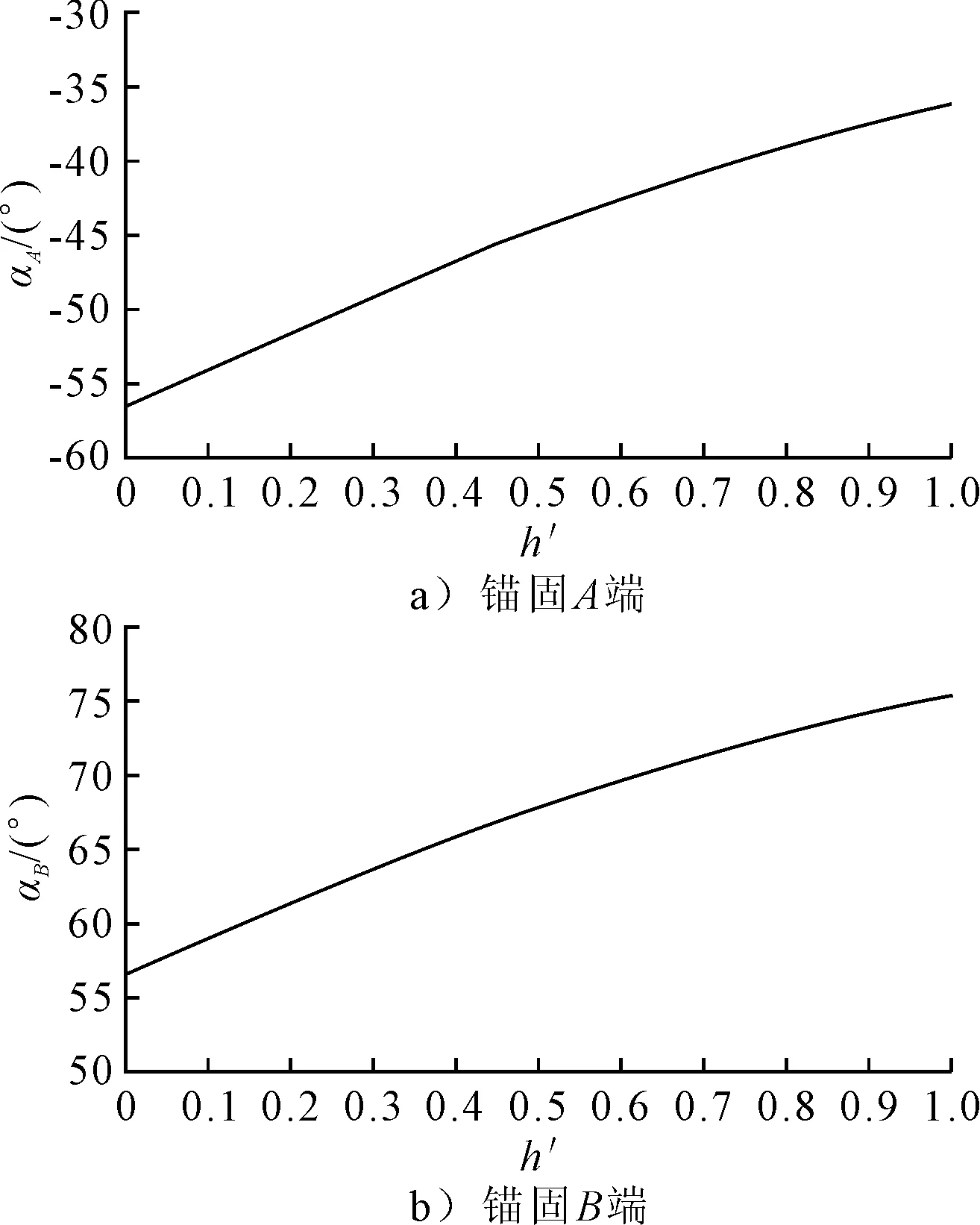
图9 不同跨接工况下管缆总长最优时两端锚固角度
从图9可知,随着高差的增大,和都逐渐增大,但绝对值不断减小。当管缆总长最优时,跨接管缆两端锚固角度绝对值之和稳定在112°左右。
3.3 无应力索长优化
工程应用中,可依跨接工况先对照图3获取最优有应力管缆差长度,再代入式(10)~(12)即可计算得到优化的无应力索长。之后结合无应力无应力自重载荷集度,带入式(13)获取有应力自重载荷集度,进而带入式(2)~(9)即可求出所有相关的各变量值。
对于跨接软管、电缆、索道等实际工程应用,当精度要求较高时,应该严格采用上述方法得先到最优有应力管缆长度,再获取管缆的无应力长度;而当精度要求不太高时,可直接依照图3优化选择跨接管缆无应力长度。
4 结论
通过对大量算例的计算结果分析得到:跨接管缆形状和静力状态受跨接工况和管缆长度影响显著;任何跨接工况下都存在一个跨接管缆最优长度,此时跨接管缆最大拉力值最小。
在工程应用中,可通过图3(或式(15))、图7和图9,快速获取任意高差不大于跨距的跨接工况下,管缆最优有应力长度,两端对应锚固角度及最小曲率半径。对于变形伸长可忽略的情况,管缆悬挂前无应力长度可近似取为管缆最优有应力长度;而对于需要更精确计算的情况,管缆无应力长度可根据式(12)计算得到。
